基于剪切耗能假设的黏弹性夹芯梁的振动和阻尼特性

第一作者黄志诚男，博士，1978年生

通信作者褚福磊男，博士，教授，博士生导师，1959年生

基于剪切耗能假设的黏弹性夹芯梁的振动和阻尼特性

黄志诚1,2，秦朝烨1， 褚福磊1

(1.清华大学机械工程系 北京100084; 2.景德镇陶瓷学院机电学院，江西景德镇333000)

摘要：基于一阶剪切变形理论和哈密顿原理建立了三层黏弹性夹芯梁结构的有限元模型并对其振动和阻尼特性进行了研究。建模时认为粘弹材料层不可压缩，振动能量是依靠黏弹性层的剪切变形来耗散的。为验证本模型的正确性，将其与解析解作了对比。同时，为了证明本方法的优越性，将其与常用的“实特征模态”、“近似复特征模态”、“钻石法”和“近似法”四种数值方法做了比较。结果表明本方法的精度在这几种数值方法中是最好的。最后，讨论了黏弹性夹芯梁结构参数变化对系统固有频率和损耗因子的影响，得到了一些有工程实际意义的结论。

关键词：振动和阻尼特性； 粘弹夹芯梁；剪切耗能；有限元

基金项目：国家自然科学基金(11272170，11102096)

收稿日期：2014-01-08修改稿收到日期：2014-03-14

中图分类号:HB53

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.07.029

Abstract:The finite element model of a three-layer viscoelastic sandwich beam was developed based on the first-order shear deformation theory and the Hamilton principle. The vibration and damping characteristics of the viscoelastic sandwich beam were studied. The viscoelastic core of the sandwich beam was considered incompressible, and the vibration energy was assumed to dissipate only by the shear deformation of the viscoelastic core. The accuracy and efficiency of the finite element model presented were verified by comparing its results with the analytical solutions. The numerical solutions of the presented method, the real eigenmodes (RM) method, the approached complex eigenmodes (ACM) method, the diamond approach (DA) and the asymptotic numerical method (ANM) were compared with the analytical solution. The results show that the presented method has better accuracy and efficiency than those commonly used numerical methods. Finally, the effects of the parameters of viscoelastic sandwich beam on its natural frequencies and loss factors were discussed. Some meaningful conclusions were provided.

Vibration and damping characteristics analysis of viscoelastic sandwich beams based on the shear dissipating energy assumption

HUANGZhi-cheng1,2,QINZhao-ye1,CHUFu-lei1(1. Department of Mechanical Engineering, Tsinghua University, Beijing 100084, China;2. College of Mechanical and Electronic Engineering, Jingdezhen Ceramic Institute,jiangxi, Jingdezhen 333001,China)

Key words:vibration and damping characteristics; viscoelastic sandwich beam; shear dissipating energy; finite element method

为了抑制梁的振动和噪声，工程上常采取的措施是构造粘弹夹芯梁。具体做法是在梁上粘贴一层具有高阻尼的黏弹性材料，然后再在该黏弹性材料上附加一层弹性材料(称之为约束层)构成三层夹芯梁结构。黏弹性材料是由高分子聚合物组成的，它有较高的耗能模量，能在相当宽的频带抑制振动和噪声，约束层的作用是增大黏弹性层的剪切变形以耗散更多的振动能量[1-4]。如果约束层的材料为普通弹性材料(一般为金属)，则这种夹层梁结构被称为“被动约束层阻尼(Passive Constrained Layer Damping，PCLD)”梁。PCLD梁结构因为结构简单，附加重量低、使用方便和效果良好的优点，在工程实际中应用广泛。图1为PCLD梁结构的示意图。

图1　PCLD梁结构 Fig.1 Schematic drawing of PCLD beam

在粘弹夹芯梁结构的研究方面，Kerwin[5]首次用简化的复模量模型对三层夹芯梁结构进行了理论分析。Ditaranto等[6-8]扩展了Kerwin的工作，他们分别推导出了PCLD梁的六阶微分方程。李恩奇等[9]用传递函数法得到了局部覆盖PCLD梁动力学问题的解析解。解析法理论上能够得到系统精确解，然而一般情况下高阶微分方程是很难求解的，而且其求解依赖于简单结构和特殊的边界条件，这一不足导致它在工程实践中难以应用。为了解决这一问题，有限元分析技术被引入到黏弹性阻尼结构的动特性分析中。Johnson等[10]在有限元软件NASTRAN中应用模态应变能法计算了粘弹夹芯梁的损耗因子。但该模态应变能法只适用于阻尼非常小的情况。Galucio等[11]用分数阶导数模型建立了夹芯梁结构的有限元方程。分数阶导数模型在一定程度上能反映粘弹材料的频变特性，但用它建立的有限元方程不易求解。Kumar等[12]用有限元法对简支夹层梁的被/主动混合控制进行了研究。石银明等[13]用GHM法对约束层阻尼梁进行了有限元分析。高淑华等[14]提出了一种粘弹夹芯结构的等效粘性阻尼算法，该方法虽然可以直接利用通用的FEM程序,但方程的求解也会受到商用软件的限制。以上研究工作均没有涉及到PCLD梁的参数变化对系统振动特性的影响。

为了弥补上述不足。本文主要进行了两个方面的工作，第一是建立了PCLD梁的有限元动力学模型。在有限元方程的推导中，合理地忽略了粘弹材料的压缩变形和整个系统的转动惯量的影响，并对能量表达式进行了规整以便推导过程更简洁和易读。后边的模型验证证明了本模型对小阻尼到大阻尼的情况均有很好的精度，相对其他常用的四种模型在精度上也更高。第二是研究了PCLD梁的参数变化对系统固有频率和损耗因子的影响。得到了一些有用的结论，对工程中PCLD梁各层厚度的配置及粘弹材料的选取均有比较好的指导意义。

1有限元建模

1.1基本假设

为便于有限元建模，提出以下基本假设条件：

(1)约束层和基梁满足欧拉-伯努利梁理论的两个假设，即变形前垂直梁中心线的平剖面，变形后仍然为平面(刚性横截面假定)和变形后横截面的平面仍与变形后的轴线相垂直。

(2)不考虑垂直于板面方向的压缩变形,认为基梁层、阻尼层、约束层有相同的挠度函数。

(3)忽略各层转动惯量的影响。

(4)结构阻尼主要由黏弹性夹芯层的剪切变形引起。

(5)各层材料之间粘贴牢固，层间无相对滑动。

(6)黏弹性层仅在线黏弹性范围内讨论。

1.2运动学关系

PCLD梁各层间的几何和变形关系如图2所示。左边是变形前，右边的变形后。

图2　PCLD梁几何和变形关系 Fig.2 Geometry and deformation of PCLD beam

图中虚线是各层中面，各几何量的意义如下：

基于以上几何和变形关系，根据一阶剪切变形理论[15]可以推导出黏弹性层的纵向位移uv和剪应变β的表达式分别为：

(1)

(2)

1.3形函数

基于前面的假设，建立PCLD梁的单元如图3所示。

图3　PCLD梁单元 Fig.3 The element of PCLD beam

该单元为一维两节点梁单元，由三层结构组成，从上到下依次为约束层，粘弹材料层和基梁层，长度为le，每个节点有4个自由度, 分别为：约束层纵向位移，基梁层纵向位移，梁的横向变形(挠度)和梁单元节点转角。

单元节点的位移矢量为

(3)

则单元内任一点的位移可以由单元的8个节点位移通过形函数插值唯一确定：

(4)

(5)

则单元4个位移分量用形函数表示为：

(6)

将式(6)分别代入式(1)和式(2)可得到用形函数表示的黏弹性层纵向位移和剪应变的表达式：

uv=[N5]{Δe}，β=[N6]{Δe}

(7)

式中,

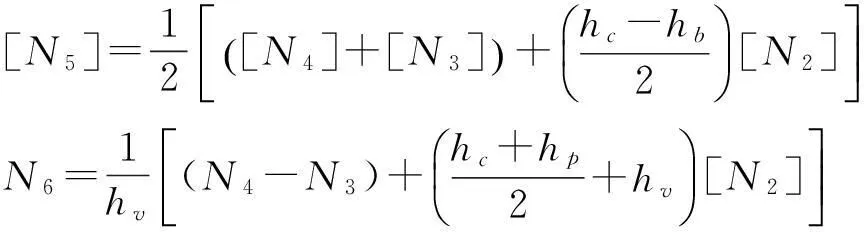
(8)

1.4能量表达式

单元能量分为势能和动能。

1.4.1单元势能

单元总势能U表达式为：

U=[Uec]+[Ubc]+[Ueb]+[Ubb]+[USv]

(9)

式中,

分别为约束层的拉伸势能和弯曲势能，基梁的拉伸势能和弯曲势能，黏弹性层的剪切势能。式(10)中，

(11)

分别为约束层的拉伸刚度矩阵和弯曲刚度矩阵,基梁层的拉伸刚度矩阵和弯曲刚度矩阵,为黏弹性层的剪切刚度矩阵。式(11)中，Ec和Eb，Ac和Ab，Ic和Ib分别为约束层和基梁的弹性模量，横截面积和转动惯量，Gv=GR+iGI=GR(1+iηv)为黏弹性材料的剪切模量，一般为复数形式，式中实部GR又叫储能模量，虚部GI又叫耗能模量，ηv是黏弹性材料的损耗因子，它是虚部和实部的比值。

单元总刚度矩阵为各层刚度矩阵之和：

[Ke]=[Kec]+[Kbc]+[Keb]+[Kbb]+[Kv]

(12)

1.4.2单元动能

单元总动能表达式如下：

T=[Tec]+[Tbc]+[Teb]+[Tbb]+[Tev]+[Tbv](13)

式中，

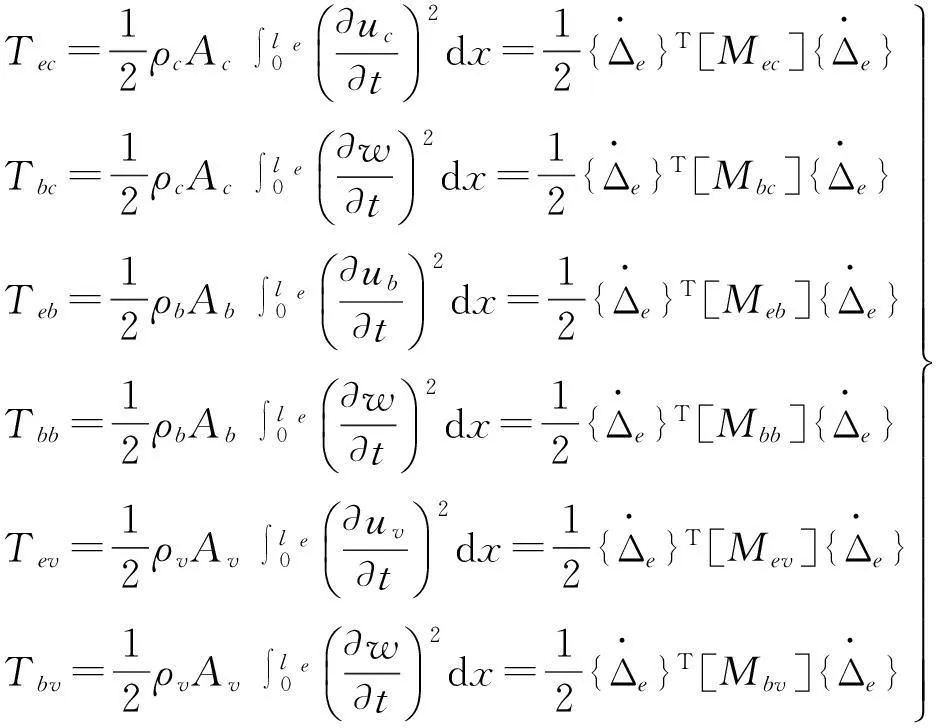
分别为约束层、基梁层和黏弹性层的拉伸动能和弯曲动能。式(14)中

(15)

分别为约束层、基梁层和黏弹性层的拉伸质量阵和弯曲质量阵。式(15)中，ρc，ρb和ρv分别为约束层，基梁层和黏弹性层的密度。

单元总质量矩阵为各层刚度矩阵之和：

[Me]=[Mec]+[Mbc]+[Meb]+

[Mbb]+[Mev]+[Mbv]

(16)

1.5PCLD梁的动力学方程

哈密顿(Hamilton)原理的变分形式为：

(17)

(18)

按有限元单元组装的方法将单元的质量阵和刚度阵组装后可得PCLD梁的动力学方程

(19)

式中，M是夹层梁的总质量阵，K是总刚度阵，Δ是总位移，R是系统所受激励力。

2特征值问题

导出PCLD梁的动力学方程后，求解其特征值问题即可得到其固有频率和损耗因子。

式(19)的特征值问题为[16]：

([K]-ω*2[M]){Δ}=0

(20)

式中，ω*为PCLD梁复特征频率。

求得复特征频率后，PCLD梁的固有频率和损耗因子[17]可以由下式计算：

(21)

3有限元模型验证

除了本文的有限元法之外，还有多种数值法来计算PCLD梁的固有频率和损耗因子，如文献[18]提出的“实特征模态”(Real Eigenmodes, RM)和“近似复特征模态”(Approached Complex Eigenmodes, ACM)法，文献[19]提出的“钻石法”(Diamant Approach，DA), 文献[20]提出的“渐近数值法”(Asymptotic Numerical Method，ANM)等。

为了验证本文有限元模型的有效性，给出了一个算例，以经典的“六阶剪切理论”解析法[21]为标准，分别用本文方法和前述RM，ACM，DA和ANM法计算该PCLD梁的固有频率和损耗因子，比较了各数值法的计算精度。

算例为一悬臂PCLD梁，约束层和基梁层为铝，黏弹性层为聚合物材料。表1给出了其材料和结构参数。

表1　PCLD梁结构的材料和结构参数

表2给出了当粘弹材料的损耗因子分别为0.1，0.6，1，1.5时，分别用解析法，RM，ACM，DA，ANM和本文方法计算的悬臂PCLD梁结构的前六阶固有频率及与解析法相比的误差。用本文有限元法计算时，将该PCLD梁结构离散为30个单元。

从表2可以看出，在计算PCLD梁结构的固有频率时， ACM，DA，ANM和本文方法均有非常好的精度，其中本文方法精度最高，最低误差为0，最大误差为0.15%，平均误差为0.08%；ACM精度次之，最低误差为0，最大为0.19%，平均误差为0.11%；DA法精度接近ACM法，最低误差为0，最高为0.19%，平均误差为0.12%；ANM法的最低误差为0，最高为3.08%，平均误差为1.36%；RM法的最低误差为0，最高为8.17%，平均误差为1.15%。虽然RM法的平均误差小于ANM法，但RM法在计算四种不同的粘弹材料损耗因子时，得到的固有频率值是一样的，这与实际不符。当然，在粘弹材料损耗因子很小时，RM法得到的结果接近解析解，但当粘弹材料损耗因子增大时，其误差也相应增大，比如当粘弹材料损耗因子增大到1.5时，其计算的一阶固有频率误差达到了8.17%，反观ANM，其误差分布非常平均，没有大的波动，所以总的来说它是精度是优于RM法的。所以可以得出结论，四种数值法在计算PCLD梁结构的固有频率时，按计算精度排序为：本文方法>ACM>DA>ANM>RM。

表2　PCLD梁结构在不同的黏弹性层损耗因子条件下的前六阶模态对应的固有频率

表3给出了当粘弹材料的阻尼因子分为为0.1，0.6，1，1.5时，分别用解析法，RM，ACM，DA，ANM和本文方法计算的PCLD梁结构的损耗因子结果及各自与解析法相比的误差。用本文有限元法计算时，同样是将梁结构离散为30个单元。

从表3可以看出，在计算PCLD梁结构的损耗因子时， ACM，DA，ANM和本文方法的精度都非常好，其中精度最好的是ACM，其最低误差为0，最大为0.68%，平均误差为0.03%；这是因为它求解复特征值问题时考虑了粘弹材料的频变特性；精度第二的是本文方法，最低误差为0，最大为2.6%，平均误差为0.39%，但本文方法用的是复常量模型，没考虑粘弹材料的频变特性，所以计算效率比ACM高，如果考虑了粘弹材料的频变特性，本文方法的精度还会有提高。DA法最低误差为0，最大为2.6%，平均误差为0.45%，稍低于本文方法。ANM法的最低误差为0，最大为10%，平均误差为2.27%，也达到了工程精度要求。RM法的最低误差为0，最高为80%，平均误差为8.46%。同样，当粘弹材料损耗因子增大时，RM法误差明显增大，当粘弹材料损耗因子增大到1.5时，RM法计算的一阶损耗因子误差达到了85%，已经不适用了。所以五种数值方法在计算PCLD梁结构的损耗因子时按精度排序为：ACM>本文方法> DA>ANM>RM。

表2和表3的计算结果验证了本文有限元模型计算PCLD梁结构固有频率和损耗因子的良好精度和效率。特别需要指出的是，应用比较多的RM法用的黏弹性材料本构关系是实数，虽然计算方便，但它低估了系统的固有频率而高估了系统的损耗因子，且当黏弹性材料的损耗因子较大时，其误差较大，所以它只适用于小阻尼状态。

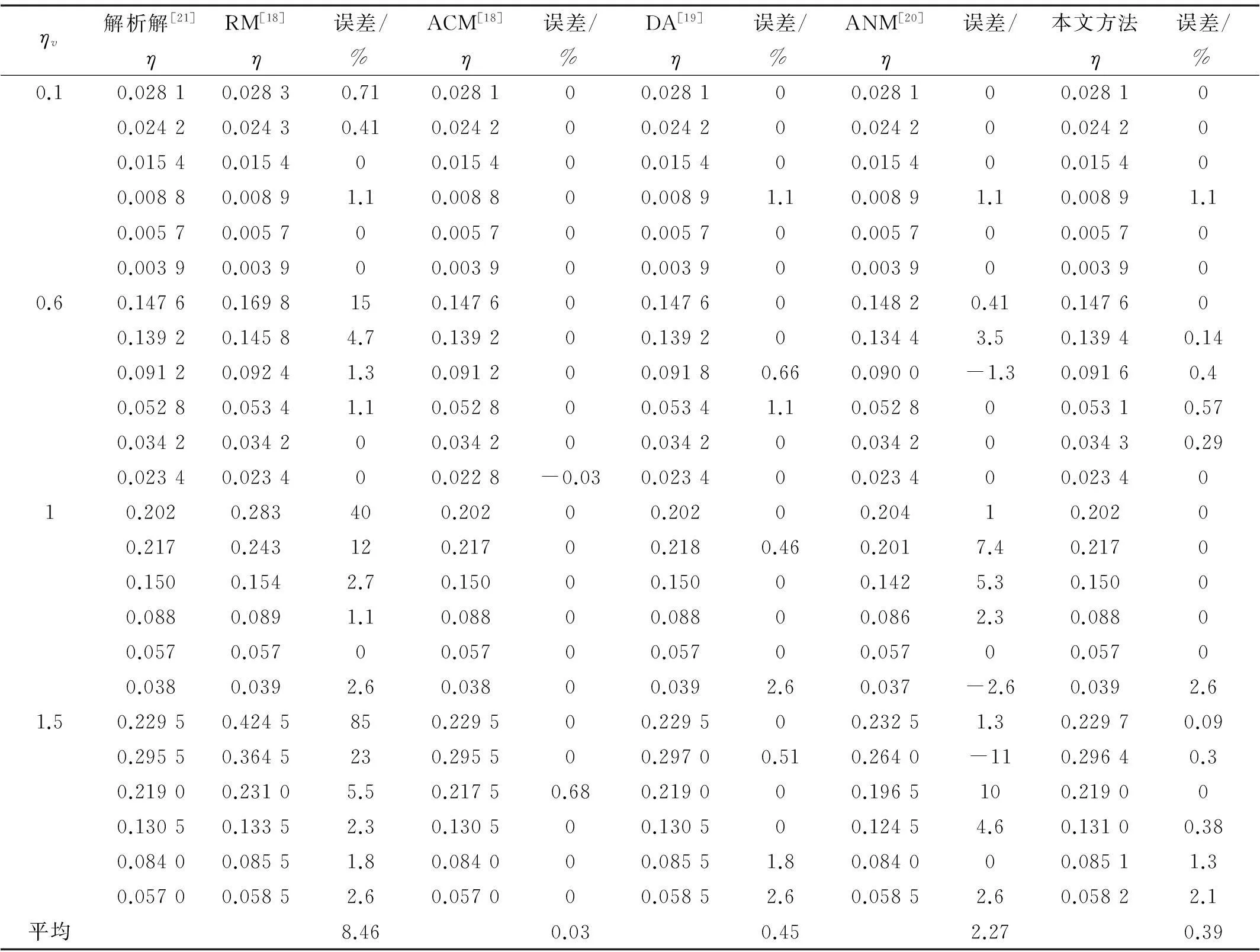
表3　PCLD梁结构在不同的黏弹性层损耗因子条件下的前六阶模态对应的损耗因子

需要说明的是，本文在进行模型验证的时候，使用的粘弹材料的本构关系是使用广泛的复剪切模量本构关系，从表2和表3中与其他方法的对比可以看出，这种本构关系虽然没有考虑材料的频变特性，但计算精度综合起来看却比另外几种考虑了材料的频变特性的模型高(只损耗因子一项比ACM法稍低，但比其他方法高)。

4参数变化对PCLD梁固有频率和损耗因子的影响

本节内容是研究粘弹材料的损耗因子、粘弹材料层厚度、约束层厚度和基梁厚度对PCLD梁的前三阶固有频率和损耗因子的影响。PCLD梁的材料和结构参数同表1，边界条件同样为一端夹持一端自由，当一种参数变化时，其他参数保持初始值不变。

4.1粘弹材料损耗因子对PCLD梁固有频率和损耗因子的影响

图4和图5分别给出了粘弹材料损耗因子ηv从0.1增大到1.5时，PCLD梁前三阶固有频率ω和损耗因子η的变化情况。

从图4可以看出，粘弹材料损耗因子ηv对PCLD梁固有频率ω影响不大，当ηv从0.1增大到1.5时，PCLD梁固有频率ω只有少量增加。这是因为粘弹材料损耗因子ηv增加会导致黏弹性层剪切模量的增加，这一关系可由式Gv=GR(1+iηv)看出，而由式(11)可知刚度与剪切模量成正比，所以黏弹性层的刚度会变大，即整个系统刚度矩阵增大，但质量没变，所以系统固有频率会增加。但由表1可以看出，黏弹性层的弹性模量数值要比另外两层低4个数量级，所以黏弹性层刚度的增加只能导致整个系统刚度少量的增加，也即只能导致系统固有频率的少许增加。

从图5可以看出，粘弹材料损耗因子ηv对PCLD梁损耗因子η有显著的影响。当ηv增加时，PCLD梁一阶损耗因子呈非线性增加，二阶和三阶损耗因子呈近似线性增加。这说明粘弹材料损耗因子ηv越大，相同条件下耗散能量越多，抑制振动和噪声的效果越好。另外三阶损耗因子的曲线形状有区别，这说明粘弹材料对梁不同模态的振动抑制效果是不一样的。

4.2黏弹性层厚度对PCLD梁固有频率和损耗因子的影响

黏弹性层厚度对PCLD梁前三阶固有固有频率和损耗因子的影响可以分别从图6和图7可以看出。为便于比较，图中横坐标是黏弹性层和基梁层厚度的比值，纵坐标分别是PCLD梁的固有频率和损耗因子。

图4 粘弹材料损耗因子变化对PCLD梁固有频率影响Fig.4TheeffectoftheviscoelasticlayerlossfactorηvonthefirstthreeordernaturalfrequenciesofthePCLDbeam图5 粘弹材料损耗因子变化对PCLD梁损耗因子影响Fig.5TheeffectoftheviscoelasticlayerlossfactorηvonthefirstthreeorderlossfactorsofthePCLDplate图6 粘弹材料层厚度变化对PCLD梁固有频率影响Fig.6TheeffectoftheviscoelasticlayerthicknesshvonthefirstthreeordernaturalfrequenciesofthePCLDbeam

从图6可以看出，当黏弹性层厚度hv增加时，系统固有频率是下降的。这是因为黏弹性层厚度增加会导致黏弹性层的刚度和质量同时增加，系统的刚度和质量也会增加，但从表1可以看出，黏弹性层的弹性模量只有另外两个弹性层的2.6×10-5倍，而其质量是另外两层的0.3倍，这说明黏弹性层厚度增加导致的系统刚度的增加要小于其导致的系统质量增加，总体效果就是导致系统固有频率下降。

从图7可以看出，黏弹性层厚度变化对系统损耗因子的影响比较复杂，和振动模态有关。当黏弹性层厚度增加时，系统的一阶模态对应的损耗因子也随着增大，但二阶和三阶损耗因子是先下降后增加的。而且当黏弹性层的厚度超过基梁层厚度时，前三阶损耗因子的变化率会变慢。这说明黏弹性层的厚度也并不是越大越好，增加黏弹性层厚度过多会导致系统质量增加，固有频率下降，但减振效果却没有很明显改善。

4.3约束层厚度对PCLD梁固有频率和损耗因子的影响

图8和图9分别给出了约束层厚度对PCLD梁系统的前三阶固有频率和损耗因子的影响。

从图8可以看出，当约束层厚度增加时，系统一阶固有频率相应增加，二阶固有频率先有一个短暂和微小的下降过程然后持续增加，三阶固有频率先明显减小然后明显上升，这说明约束层厚度对梁各阶固有频率的影响也和模态有关。

从图9可以看出，当约束层厚度增加时，系统前三阶损耗因子均是先增加后减小。但是前三阶损耗因子最大值对应的约束层厚度不同，当约束层厚度与基梁层厚度之比约为1.2时，一阶损耗因子有最大值，当约束层厚度与基梁层厚度之比约为0.8时，二阶和三阶损耗因子有最大值。

图7 粘弹材料层厚度变化对PCLD梁损耗因子影响Fig.7TheeffectoftheviscoelasticlayerthicknesshvonthefirstthreeorderlossfactorsofthePCLDbeam图8 约束层厚度变化对PCLD梁固有频率影响Fig.8TheeffectoftheconstraininglayerthicknesshconthefirstthreeordernaturalfrequenciesofthePCLDbeam图9 约束层厚度变化对PCLD梁损耗因子影响Fig.9TheeffectoftheconstraininglayerthicknesshconthefirstthreeorderlossfactorsofthePCLDbeam

4.4基梁层厚度对PCLD梁固有频率和损耗因子的影响

基梁层厚度对PCLD梁前三阶固有频率和损耗因子的影响可分别从图10和图11看出。

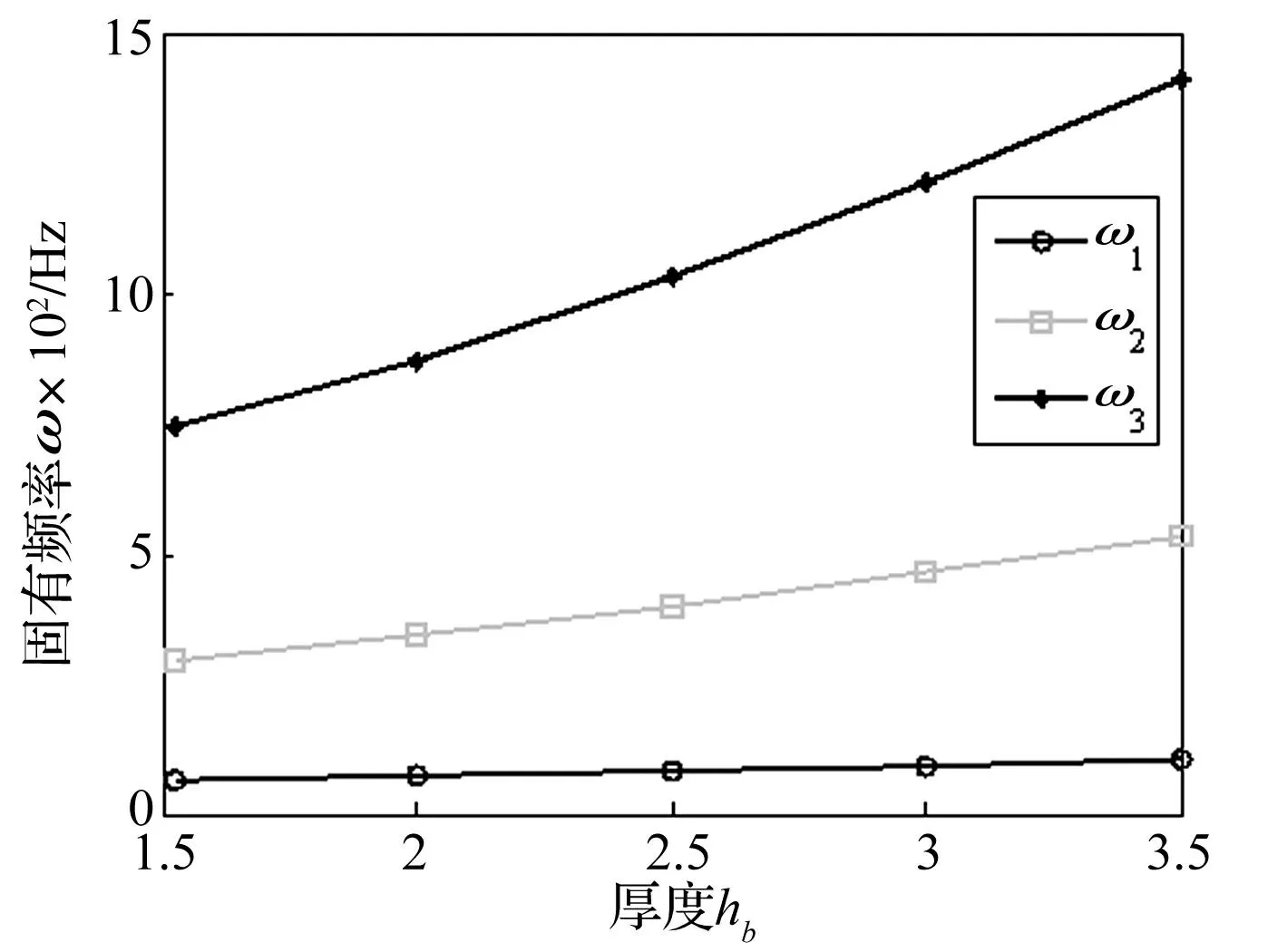
图10　基梁厚度变化对PCLD梁固有频率的影响 Fig.10 The effect of the base beam thickness h bon the first three order natural frequencies of the PCLD beam

图11　基梁厚度变化对PCLD梁损耗因子的影响 Fig.11 The effect of the base beam thickness h bon the first three order loss factors of the PCLD beam

从图10可以看出，当基梁层厚度增加时，系统前三阶固有频率均增加。这是因为当基梁层厚度增加时，系统刚度和质量均增加，但刚度增加速度超过质量增加速度。但各阶固有频率增加的速度不一样，第三阶固有频率增加最快，其次是第二阶和第一阶。

从图11可以看出，随着基梁层厚度的增加，系统损耗因子快速降低。这是因为基梁越厚，相同条件下其振动能量越大，则衰减越困难，也就是其振动越难以抑制，所以系统损耗因子下降。

5结论

基于一阶剪切变形理论和哈密顿原理建立了PCLD梁的有限元模型并研究了其振动和阻尼特性。建模所用的单元为两节点八自由度梁单元。黏弹性材料的本构关系用的是常复数模量模型且黏弹性层被假定为不可压缩的。

通过一个具体的算例验证了本文有限元法的有效性。以解析法作标准，将本文有限元法和另外四种常用数值方法RM，ACM，DA，ANM法的计算精度做了对比分析，结果表明本文方法在预测PCLD梁系统的固有频率和损耗因子方面具有良好的精度和效率，综合效果优于其他方法。特别需要指出的是常用于模态应变能方法的RM法只适用于阻尼非常小或者黏弹性成分非常小的场合，在较大阻尼状态下不适用。

最后，研究了黏弹性层损耗因子、黏弹性层厚度、约束层厚度和基梁层厚度的变化对PCLD梁系统前三阶固有频率和损耗因子的影响，得到以下结论：

(1)黏弹性层损耗因子对系统固有频率影响不大，但对系统损耗因子有显著影响。

(2)黏弹性层厚度的增加会导致系统固有频率减小，其对系统的损耗因子的影响和模态有关，会导致一阶损耗因子增大，但第二阶和第三阶损耗因子是先下降后缓慢增大的。

(3)当约束层厚度增加时，系统一阶固有频率相应增加，二阶固有频率先有一个短暂和微小的下降过程然后持续增加，三阶固有频率先明显减小然后明显上升，系统前三阶损耗因子均是先增加后减小。

(4)基梁层厚度增加会导致系统固有频率增大和损耗因子的明显减小。

验证结果表明本文建立的有限元模型在预测PCLD梁系统的固有频率和损耗因子方面具有良好的精度和效率，综合效果优于其他常用方法。是能够应用于工程实际的。另外本文开展的参数影响分析结果对工程中PCLD梁各层厚度的配置及粘弹材料的选取均有比较好的指导意义。

本文研究的PCLD梁的黏弹性层比较薄，而且考察的也是自由振动。在这种条件下，复剪切模量本构关系完全能满足工程应用需要。但是如果PCLD梁在黏弹性层较厚或者是在复杂载荷的条件下的振动，复剪切模量本构关系可能不能很好地反映粘弹夹芯梁的动力响应，这时就要寻找能更好地模拟粘弹材料频变特性的本构关系表达式并将其结合到有限元模型中，笔者会在后续工作中关注这一问题。

参考文献

[1]Grootenhuis P. The control of vibrations with viscoelastic materials[J]. Journal of Sound and Vibration, 1970，11(4): 421-433.

[2]Trindade A T. Hybrid active-passive damping treatments using viscoelastic and piezoelectric materials: review and assessment[J]. Journal of Vibration and Control, 2002, 8:699-745.

[3]Trindade M A. Experimental analysis of active-passive vibration control using viscoelastic materials and extension and shear piezoelectric actuators[J]. Journal of Vibration and Control, 2011, 17(6) 917-929.

[4]Nakra B C. Vibration control in machines and structures using viscoelastic damping[J]. Journal of Sound and Vibration, 1998, 211(3):449-465.

[5]Kerwin E M. Damping of flexural waves by a constrained viscoelastic layer[J]. Journal of the Acoustical Society of America, 1959, 31(7):952-962.

[6]Ditaranto R A. Theory of vibratory bending for elastic and viscoelastic layered finite length beams[J]. Journal of Applied Mechanics, 1965, 87:881-886.

[7]Mead D J, Markus S. The forced vibration of a three-layer damped sandwich beam with arbitrary soundary conditions[J]. Journal Sound and Vibration 1969, 10(2):163-175.

[8]Rao D K. Frequency and loss factors of sandwich beams under various boundary conditions[J].Journal of Mechanical Engineering Science, 1978, 20(5): 271-282.

[9]李恩奇, 唐国金, 李道奎,等. 局部覆盖约束层阻尼梁动力学问题的解析解[J]. 振动与冲击，2007，26(5)：85-89.

LI En-qi, TANG Gao-jin, LI Dao-kui, et al. Analytical solution for a beam with partially covered constrained layer dampling[J]. Journal of Vibration and Shock, 2007，26(5)：85-89.

[10]Johnson C D, Kienholz D A. Finite element prediction of damping in structures with constrained layers[J].AIAA J, 1982,120(9):1284-129.

[11]Galucio A C, Deü J F, Ohayon R. Finite element formulation of viscoelastic sandwich beams using fractional derivative operators[J]. Computational Mechanics, 2004, 33: 282-291.

[12]Kumar N, Singh S P. Vibration and damping characteristics of beams with active constrained layer treatments under parametric variations[J]. Materials and Design, 2009, 30: 4162-4170.

[13]石银明,华宏星,傅志方. 约束层阻尼梁的有限元分析[J]. 上海交通大学学报, 2000, 34(9):1289-1290.

SHI Yin-ming, HUA Hong-xing, FU Zhi-fang. Finite element analysis of constrained layer damping beams[J]. Journal of Shanghai Jiaotong University, 2000, 34(9):1289-1290.

[14]高淑华,赵阳,李淑娟，等.黏弹性结构动力学分析的等效粘性阻尼算法[J]. 振动与冲击，2005，24(1)：18-27.

GAO Shu-hua, ZHAO Yang, LI Shu-juan, et al. Equivalent visco-damping method for the dynamic response analysis of visco-elastic structure[J]. Journal of Vibration and Shock, 2005, 24 (1): 18-27.

[15]Baber T T, Maddox V R, Orazco C E. Finite element model for harmonically excited viscoelastic sandwich beams[J]. Computers & Structures, 1998, 66(1): 105-113.

[16]Daya E M, Potier-Ferry M. A numerical method for nonlinear eigenvalue problems application to vibrations of viscoelastic structures[J]. Computer and Structure, 2001,79(5):533-541.

[17]Kumar S, Kumar R, Sehgal R. Enhanced ACLD treatment using stand-off-layer: FEM based design and experimental vibration analysis[J]. Applied Acoustics, 2011, 72: 856-872.

[18]Bilasse M, Daya E M, Azrar L. Linear and nonlinear vibrations analysis of viscoelastic sandwich beams[J]. Journal of Sound and Vibration, 2010, 329(23): 4950-4969.

[19]Bilasse M, Charpentier I, Daya E M, et al, A generic approach for the solution of nonlinear residual equations. Part II: homotopy and complex nonlinear eigenvalue method[J]. Computer Methods in Applied Mechanics and Engineering, 2009, 198: 3999-4004.

[20]Abdoun F, Azrar L, Daya E M，et al. Forced harmonic response of viscoelastic structures by an asymptotic numerical method[J]. Computers and Structures, 2009, 87:91-100.

[21]Soni M L. Finite element analysis of viscoelastically damped sandwich structures[J]. Shock Vibrat. Bull, 1981, 55 (1):97-109.