某转管机枪机心部件动力学特性分析与改进研究

第一作者化斌斌男，博士生，1987年生

通信作者王瑞林男，教授，博士生导师，1963年生

某转管机枪机心部件动力学特性分析与改进研究

化斌斌1，王瑞林1，李涛2，范智滕1，李永建1

(1.军械工程学院火炮工程系，石家庄050003； 2.防空兵学院高炮系， 郑州450052)

摘要：以某型转管机枪为研究对象，为了分析解决该型机枪在样机试验中出现的机心头断裂、机心卡死以及闭锁开锁时接触面强度不足等故障现象，首先对机心部件开闭锁过程进行了受力分析；其次利用多体动力学分析软件建立了机枪系统的动力学模型，重点对机心运动过程进行了动力学计算；然后利用有限元分析软件建立了机心部件运动过程中的动态应力与位移分析模型，在满足机枪射频要求的前提下，得出开闭锁过程中接触面关键位置的应力与位移的变化曲线；最后综合研究分析得到的动力学响应特性和应力、位移云图，分析找出引发故障的根本原因，对机心头进行了结构改进，有效提高了机枪的射击可靠性，为机心部件的优化改进提供了理论依据与试验指导。

关键词：转管机枪；机心部件；动力学仿真；有限元

收稿日期：2014-09-16修改稿收到日期：2014-11-19

中图分类号:TJ21

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.07.028

Abstract:To analyze and solve the breakdown of a certain Gatling gun in prototype experiments such as bolt fracture, core seizing and insufficient strength of interface while locking and unlocking, the bolt forces in the lock-unlock process were analyzed, the dynamic model of a Gatling gun system was established by means of multi-body dynamics software and the bolt movement process was calculated, the dynamic stress and displacement analysis model was built using the finite element software, and then the stress and displacement curves at the key interface positions in the bolt lock-unlock process were obtained under the condition of fire frequency demand, the fault causes were found out by synthesizing the response characters, stress and displacement nephograms, and the bolt structure was improved which effectively increases shooting reliability and provides the theory basis and test direction for optimizing the bolt assembly.

Dynamic characteristics and improvement of the bolt assembly of Gatling gun

HUABin-bin1,WANGRui-lin1,LITao2,FANZhi-teng1,LIYong-jian1(1.Department of guns engineering, Ordnance Engineering College, 050003, Shijiazhuang;2. Department of Antiaircraft Gun, Air Defense Forces Academy, 450052, Zhengzhou)

Key words:Gatling gun; bolt assembly; dynamic simulation; finite element

转管机枪采用导气式自动机的基本原理，利用发射时气室内高温、高压火药燃气压力作用于活塞滑板机构并驱动机心体和身管旋转，从而完成自动机循环动作以实现连续射击[1]。由于转管机枪主要依靠高射速来完成对目标的有效打击和毁伤，其发射原理和结构与一般枪械有很大的不同[2-3]，开闭锁动作中的机心运动情况和受力状态非常复杂，所以对其可靠性就需要特别关注[4]。转管机枪在研制阶段曾出现过开闭锁凸轮变形、机心卡死、机心体接触面强度不足等故障现象，机心部件作为机枪的重要部件，其结构是否合理、强度能否满足要求，关系到该机枪系统工作的可靠性和射击过程的安全性。

为了研究分析机心部件在样机试验中出现的故障问题，本文从多体系统动力学出发，考虑武器在实际射击过程中的受力情况和边界条件，利用多体动力学软件建立了机枪系统的仿真模型，重点对机心部件运动过程进行了动力学计算；然后从应力角度出发，利用有限元分析软件建立了机心部件的有限元动态仿真模型，通过观察仿真结果，分析产生故障的原因，对机心部件进行改进设计，靶场试验验证了改进后的结构可有效提高机枪的射击可靠性，为样机的改进与优化提供了依据。

1机心部件受力分析

1.1闭锁过程受力分析

机心部件主要包括机心体、机心头和击针等构件。以枪管轴线指向枪口方向为X轴正向，在射击过程中，机心驱动滚轮在行星体外周的曲线槽内沿逆时针方向强迫运动，带动机心部件随机心匣在YZ面内旋转，当机心头上的闭锁面与机心匣上的闭锁凸轮碰撞时运动受阻，迫使其绕机心轴线O点自转，并回转一定角度实现闭锁。以机心匣为基础构件，添加驱动力矩为Mr，在机心头自转的反方向添加达朗伯尔力矩，标记为MR，以机心匣为受力体，使机构处于平衡状态，如图1(a)所示。

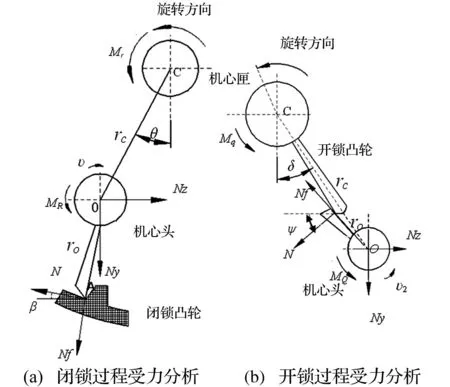
图1　开闭锁时受力分析 Fig.1 Force analysis in the lock-unlock process

对机心匣中心线上C点求解平衡力矩，则

Mr=Nzrccosθ+Nyrcsinθ

(1)

以机心头为受力体，不考虑机心体与机心头的摩擦阻力，对O点力矩平衡，可以得出

MR=Nro

(2)

对Z方向受力平衡，则

Nz=Ncosβ+Nfsinβ

(3)

对Y方向受力平衡，则

Ny=Nsinβ-Nfcosβ

(4)

综合以上各公式，可以得出

(5)

式中，rc机心旋转中心到机心匣旋转中心的距离；ro机心中心到闭锁点的高度；f为机心头与闭锁凸轮之间的摩擦系数。

1.2开锁过程受力分析

机心部件随机心匣旋转过程中，当机心头上的开锁面与机心匣上的开锁凸轮碰撞时，机心头运动受阻并绕机心轴线O点自转，并沿闭锁反方向(图中箭头v2所示方向)回转一角度实现开锁，开锁过程受力分析如图1(b)所示。

对机心匣中心线上C点求解平衡力矩，则

Mq=Nzrccosδ-Nyrcsinδ

(6)

以机心头为受力体，不考虑机心体与机心头的摩擦阻力，对O点力矩平衡，可以得出

MQ=Nro

(7)

对Z方向受力平衡，则

Nz=Ncosψ+Nfsinψ

(8)

对Y方向受力平衡，则

Ny=Nfcosψ-Nsinψ

(9)

综合以上各公式，可以得出

(10)

式中，rc机心旋转中心到机心匣旋转中心的距离；ro机心中心到开锁点的高度；f为机心头与开锁凸轮之间的摩擦系数。

2虚拟样机模型建立

为了更加真实的仿真机心部件在机枪射击过程中的运动状态与受力情况，首先利用实体造型软件建立了该枪完整的三维实体模型，然后通过Mechanism/Pro模块导入到动力学软件中。建模过程中，考虑射手边界条件与驻锄-土壤参数关系模型对机枪的动力学特性产生影响，并且利用刚柔耦合多体系统动力学理论，将刚度小、易发生大变形的零部件按柔性体进行计算，建立了该转管机枪整枪的仿真模型，如图2所示。

图2　转管机枪的虚拟仿真模型 Fig.2 Virtual simulation model of gatling gun

2.1载荷的确定与约束添加

机枪在射击的状态下承受的外力主要有枪膛合力、气室压力、气室压力反力、脱弹阻力、弹带阻力、抽壳阻力以及自身产生的摩擦阻力和各种弹簧的作用力[5,6]。各种弹簧的作用在建立运动副的过程中已经加入，只需改变其刚度系数和预压力至实际情况即可；枪膛合力、气室压力和各种阻力的大小可以通过相应的计算公式作为外力添加进去，其中气室压力曲线如图3所示。

图3　气室压力曲线 Fig.3 Gas chamber pressure graph

选择机枪储能装置内齿轮为参照系。如前文所述，以枪管轴线指向枪口方向为X轴正向，以竖直向上为Y轴正向，以右手准则确定Z轴正向。根据该机枪的物理样机约束关系，添加约束副，整个机枪模型中共包含172个运动构件，142个固定副、27个旋转副、9个平移副、1个圆柱副、1个齿轮副和54个实体碰撞，99个自由度。机心部件的约束关系模型如图4所示。

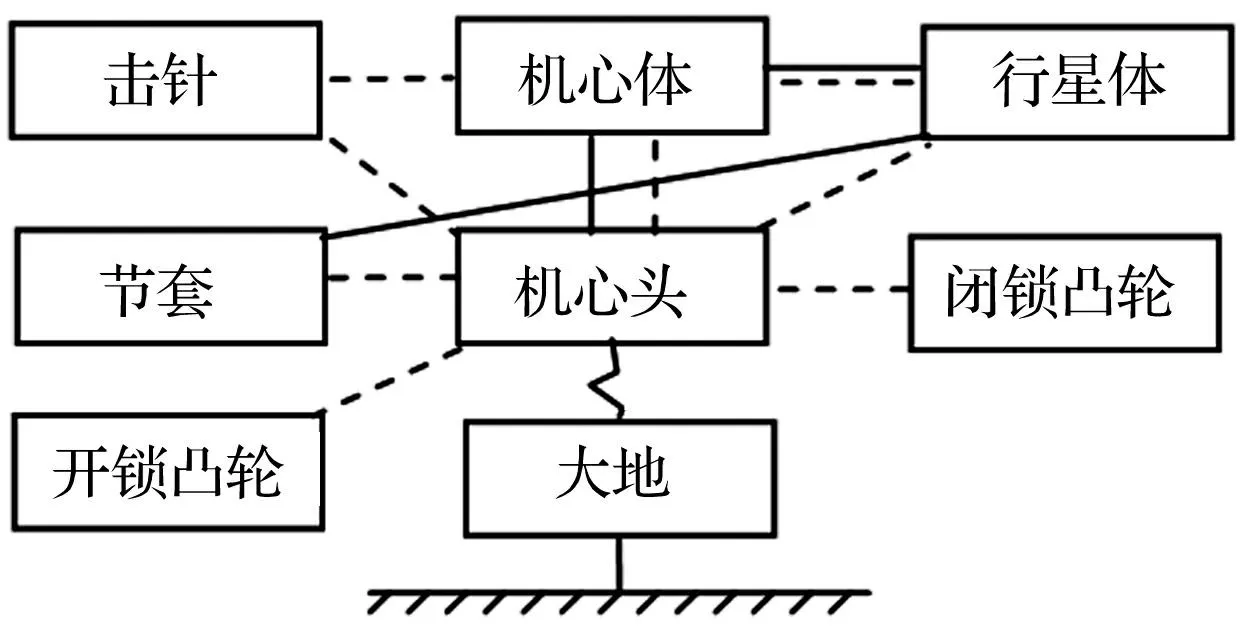
图4　机心部件约束关系模型 Fig.4 The constraint relational model of bolt assembly

其中，机心头与机心体之间以圆柱副和碰撞副连接；机心头与大地之间添加枪膛合力作用，方向为X轴负向(即后坐方向)；机心头与节套、行星体、开锁凸轮、闭锁凸轮、击针之间均以碰撞副连接；机心体与行星体之间主要以滑移副和碰撞副连接；机心体与击针之间以碰撞副连接；节套与行星体之间通过固定副连接。

2.2机心部件运动计算

考虑了机心部件运动过程中接触面间的摩擦，取动摩擦系数为0.1。利用所建立的虚拟样机，在气室压力的驱动和枪膛合力的作用下，可以得到机心部件在射击过程的运动和受力情况，取0.3 s内仿真结果如图5～7所示。

图5　开闭锁过程中机心头在Z方向受力情况 Fig.5 Z direction force of the bolt in the lock-unlock process

图6　开闭锁过程中机心头在Y方向受力情况 Fig.6 Y direction force of the bolt in the lock-unlock process

图7　机心头在运动过程中受到的枪膛合力 Fig.7 Join force of the chamber in the bolt movement process

为了更好地观察机心头在一次开闭锁过程中的瞬间受力曲线特征，对图5中0.255 s～0.29 s时间段进行放大处理，如图8所示。

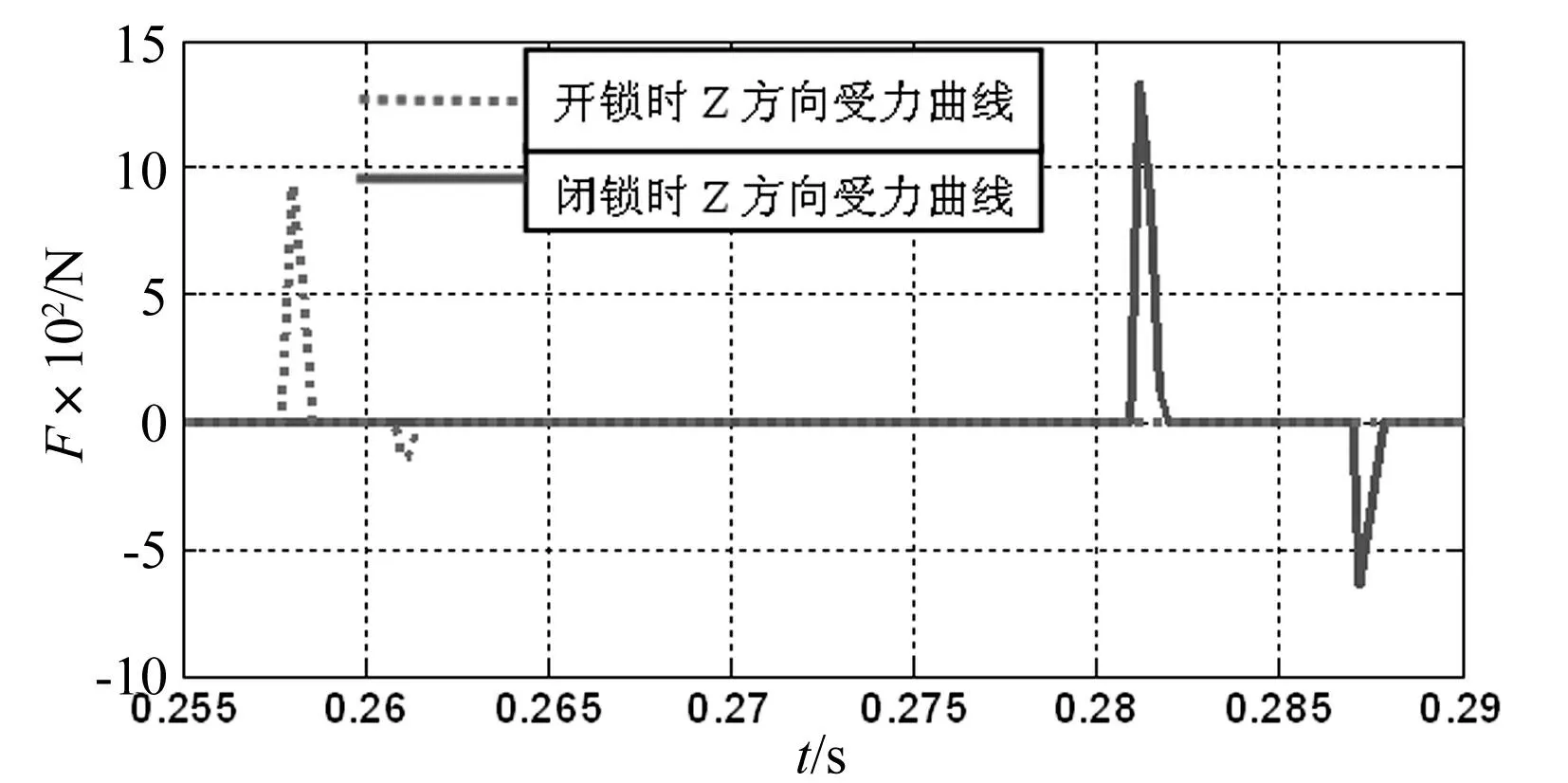
图8　对图5中机心头受力情况局部放大 Fig.8 Partial enlargement of force situation of Fig.5

由图5～8可以看出：机心部件在一个开闭锁运动过程中，机心头首先与闭锁凸轮支撑面碰撞，受到Z轴正向和Y轴正向的瞬时作用力，迫使机头体在节套槽内逆时针旋转，完成闭锁击发动作；当击发动作完成后，经过约0.011 2 s，机心头与开锁凸轮开锁面发生碰撞，产生一个Z轴正向、Y轴负向的瞬时作用力，迫使机头体在节套槽内顺时针旋转，完成开锁动作。同时，从受力曲线可以看出：当机心头与闭锁凸轮发生碰撞后，经过约0.007 s时间后，机心头回转过程中再次与闭锁凸轮碰撞，在Z轴负向和Y轴正向产生瞬时作用力；机心头与开锁凸轮发生碰撞后，经过约0.005 s后，机心头开锁过程中再次与开锁凸轮接触产生Z轴负向和Y轴负向的瞬时作用力。这两个作用力都会造成机心头发生变形并在枪管高速旋转时导致机心头在节套内回转时在轴线方向出现偏转，发生机心卡死故障。

3机心部件有限元模型的建立与仿真

运用有限元分析软件对机心部件运动过程进行了非线性动力学分析，以接触碰撞理论为基础，模拟机心头、机心体随着节套与行星体旋转并同时与开闭锁凸轮、节套等产生碰撞的整个过程，机枪稳定射频为每分钟3000发子弹，节套与行星体旋转速度设定为机枪达到稳定射频时的角速度，通过输入测量数据曲线确定。根据在前文中得出的机心部件的受力情况，主要分析了机心头的应力和变形状态，从而为该机构的改进设计提供依据，同时验证了该设计的可行性。

3.1有限元模型的建立

鉴于节套、行星体、驱动轮曲线槽、开闭锁凸轮等几何形状的复杂性，为了有效地进行有限元建模并减小计算任务量，对一些圆角、倒角、凹槽、凸台等细部特征进行了删除或抑制工作；而对远离主要受力部位的几何特征，在保留整体刚度基本不变的条件下，对结构进行了简化。对于机心部件以及与其相接触的零件部位，尤其是严重影响受力状态的部位，不改变结构上的倒角、圆角、切面等特征，以保证分析结果的真实性与准确性。最后将简化后的三维实体模型导入到有限元软件中，添加材料属性，其中弹性模量为206 GPa，泊松比为0.28，密度为7 800 kg/m3。节套、行星体、曲线槽等零件与机心部件相互接触，对模型起作用的仅是结构的外表面，因此将其均作为壳体进行处理。

图9　机心部件的有限元模型 Fig.9 The finite element model of bolt assembly

在本问题中，为了保证网格的质量避免求解过程中的网格畸变并考虑到机心头几何模型的复杂性，机心头采用了四节点四面体单元[7-8]。在划分的过程中，对预计将产生应力集中的部位或者有可能产生破坏的部位，进行网格细化；利用8节点的六面体单元对节套、行星体等进行网格划分，整个模型共生成97 846个单元。边界条件为：节套与行星体之间为固定约束，沿X轴线逆时针方向旋转。为反映在枪膛合力作用下机心的受力状态，将膛内火药燃气的压力等效为机心头受力面单元上的平均压力，并根据最大膛压和弹壳的有关尺寸，确定压力载荷值，其他零件的边界条件按照上文图4中描述进行设置，定义相关的分布耦合约束和分析步。所建立的有限元模型如图9所示。

3.2仿真结果与分析

对于上面建立的机心部件的有限元仿真模型，经过分析求解，设定仿真时长为0.06 s，可以得到机心头等零件在行星体外周曲线槽内旋转一周过程中不同时刻的应力和位移云图。机心头不同时刻应力与位移云图分别如图10(a-d)所示。

图10　机心头运动过程中应力和位移云图 Fig.10 Stress and displacement nephograms in the bolt movement process

从仿真得到的应力与位移云图可以看出，机心头与闭锁凸轮发生碰撞出现在23.4 ms时刻，此刻碰撞面等效应力的最大值出现在图10(a)的椭圆线位置(标记为A)，同时在机心头抽壳部位出现了高应力区，而最大变形值出现在碰撞面与弹底抽壳的位置，这也与样机试验中出现的机头拉壳钩断裂，导致推弹阻力增大的情况吻合；机心头与开锁凸轮发生碰撞出现在32.6 ms时刻，此刻碰撞面等效应力的最大值出现在图10(b)的椭圆线位置(标记为B)，同时在机心头与节套接触的过度部位出现较大的应力值，而最大位移值出现在机心头与开锁凸轮碰触的位置，并沿着机头体圆周方向规律的减小。根据机心头运动过程中接触面标记位置A与B的应力随时间变化的历程曲线，如图11(a-b)所示。

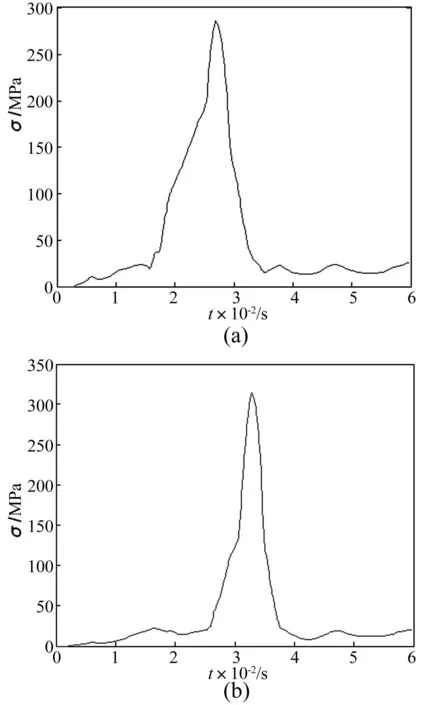
图11　机心头运动过程中A、B标记点应力时间曲线 Fig.11 Stress curves of A and B marks in the bolt movement process

从图11中A与B的应力时间曲线可以看出：①在26.9 ms时，A附近所选择单元的等效应力出现最大值，为285.3 MPa；②在33.8 ms时，B附近所选择单元的等效应力出现最大值，为314.4 MPa。

通过机心部件的动力学计算与有限元分析发现：机心头在开闭锁动作完成后，经过一定时间仍然与开闭锁凸轮产生二次碰撞，出现了比较明显的应力集中现象，并且在多次射击的碰撞冲击作用下容易发生疲劳破坏，可以通过改进机心头与开闭锁凸轮接触面的结构来减小二次碰撞。同时，通过观察机心头运动过程的应力位移云图发现，在机心头闭锁回转完成后与节套接触时，在其过渡部位有应力集中现象出现，可以通过改进过渡角来消除应力集中现象，对于提高机心头的强度是有利的。结合仿真与试验中出现的故障问题，对机心头结构进行了改进，改进前与改进后方案如图12所示。

图12　机心头结构改进前方案与改进后方案 Fig.12 Unimproved structure and improved structure of the bolt

图12中对机心头改进的部位进行了标注，1-6分别对机心头过渡部位和接触面进行了局部倒角和切除操作。通过样机靶场试验发现，机心头结构改进后能够有效消除开闭锁凸轮产生的二次碰撞并减小应力集中，机心头运动过程中出现的机头断裂、机心卡死现象得到了有效的抑制，提高了机枪射击的可靠性。

4结论

本文通过多体动力学和有限元分析软件建立了某型转管机枪完整的仿真模型和机心部件的有限元模型，通过动力学模型和有限元模型的有效结合，能够更加真实地反映机心部件的运动过程和受力情况，并通过分析观察仿真结果，找出了机心部件在试验中出现故障的根本原因，对机心头的结构进行了改进设计，提高了机枪系统工作的可靠性和安全性，同时也为机心部件结构的进一步优化提供了参考。

参考文献

[1]戴成勋, 靳天佑, 朵英贤. 自动武器设计新编[M]. 北京： 国防工业出版社, 1990:220-227.

[2]葛藤, 赵军, 周克栋. 某新型自动步枪闭锁机构动应力分析[J]. 弹道学报,2006,18(2):36-39.

GE Teng, ZHAO Jun, ZHOU Ke-dong. Analysis of dynamic stress of a new rifle locking mechanism[J]. Journal of Ballistics, 2006, 18(2): 36-39.

[3]胥勇清, 杨臻, 王自勇. 某外能源转管机枪机心组动力学仿真分析[J]. 火炮发射与控制学报,2006,(1):45-49.

XU Yong-qing, YANG Zhen, WAQNG Zi-yong. Dynamic simulation and analysis on bolt system of prototype of an external energy gatling machine gun[J]. Journal of Gun Launch and Control, 2006, (1): 45-49.

[4]郝秀平, 薄玉成, 徐建.某转管武器机芯应力有限元分析[J].中北大学学报,2010,31(2):147-151.

HAO Xiu-ping, BO Yu-cheng, XU Jian. Finite element stress analysis for gatling gun bolt[J].Journal of North University of China, 2010, 31(2): 147-151.

[5]徐诚，王亚平.火炮与自动武器动力学[M].北京：北京理工大学出版社,2006.

[6]陈明,马吉胜,贾长治,等. 基于ADAMS 的某型通用机枪动力学建摸与仿真[J]. 系统仿真学报, 2006, 18(7): 2046-2048.

CHEN Ming, MA Ji-sheng, JIA Chang-zhi, et al. High virtual prototyping of dualpurpose machine gun based on ADAMS and Simulation[J]. Journal of System Simulation,2006, 18(7): 2046-2048.

[7]王勖成. 有限单元法[M]. 北京：清华大学出版社, 2003, 666-700.

[8]冯伟, 周新聪, 严新平,等. 接触问题实体建模及有限元法仿真实现[J]. 武汉理工大学学报, 2004, 26(6): 52-55.

FENG Wei, ZHOU Xin-cong, YAN Xin-ping, et al. The entity modeling of contact problem and its simulation realization by finite element method[J]. Journal of Wuhan University of Technology, 2004, 26(6): 52-55.