自立式高耸结构风振控制方法研究

第一作者陈鑫男，博士，讲师，1983年生

通信作者李爱群男，博士，教授，博士生导师，1962年生

自立式高耸结构风振控制方法研究

陈鑫1,李爱群2,王泳3,张志强2

(1. 苏州科技学院江苏省结构工程重点实验室，江苏苏州215011； 2. 东南大学混凝土及预应力混凝土结构教育部重点实验室，南京210096； 3. 苏州云白华鼎烟囱制造有限公司，江苏苏州215003)

摘要：针对自立式高耸结构的风振控制装置及其设计方法开展研究。首先，根据自立式高耸结构的特点，设计了环形TMD、TLD和TLCD三种调频减振装置，并推导了其力学模型；随后，基于等效阻尼比的概念和我国规范的抗风设计方法，建立了自立式高耸结构风振控制的统一设计方法；最后，针对数值算例，进行了风振控制装置设计，并通过时程分析方法验证了该方法的有效性。研究结果表明，所设计的三种环形调频减振装置适用于自立式高耸结构的风振控制，建立的简化设计方法与时程分析的结果平均误差仅为5.37%，具有较高的精度，可用于自立式高耸结构的风振控制设计。

关键词：自立式高耸结构；风振控制；TMD；TLD；TLCD

基金项目：江苏省高校自然科学研究项目(13KJB560012)

收稿日期：2013-10-21修改稿收到日期：2014-04-16

中图分类号:TU318; TU312; TU973+.2

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.07.024

Abstract:Damping devices and their design methods used in self-standing high-rise structures under wind loads were studied. According to the characteristics of self-standing high-rise structures, three tuned frequency damping devices (ring shape tuned mass damper, ring shape tuned liquid damper and ring shape tuned liquid column damper) were designed, and their mechanical models were deduced. On the basis of the equivalent damping concept and the wind resistance design methods in China codes, unified design methods of these damping devices used in self-standing high-rise structures were proposed. The wind-induced vibration control devices of two numerical expamples were presented using the proposed design method, whose effectiveness was confirmed by time history analysis. The study shows that the three ring shape damping devices designed in the paper are applicable to the vibration control of self-standing high-rise structures, and the analysis results show that the mean relative error between the results using equivalent damping method and time history analysis method is only 5.37%, so the proposed design method has a high precision, and can be used for the vibration control of self-standing high-rise structures under wind loads.

Investigation on techniques for wind-induced vibration control of self-standing high-rise structures

CHENXin1,LIAi-qun2,WANGYong3,ZHANGZhi-qiang2(1. Jiangsu Key Laboratory of Structure Engineering, Suzhou University of Science and Technology, Suzhou 215011, China2. Key Laboratory of Concrete and Prestressed Concrete Structure of Ministry of Education, Southeast University, Nanjing 210096, China3. Suzhou Rainbow Huading Chimney Manufacturing Co.Ltd., Suzhou 215003, China)

Key words:self-standing high-rise structure; wind-induced vibration control; TMD; TLD; TLCD

近年来，随着国民经济的发展和城镇化的推进，基础设施的建设过程中对各种自立式高耸结构(风力发电机、输电塔、通信塔、烟囱、高杆灯等)的需求日益增加。与普通高耸结构相比，自立式高耸结构，特别是那些超高、大长细比的结构，往往具有结构柔、质量轻、阻尼小等独特性能。这些都造成了这类结构通常对风荷载极其敏感[1]，风荷载导致的持续剧烈振动不仅无法维持结构的正常使用，还将使结构应力过大，形成疲劳裂纹，最终在强风作用下导致结构的破坏，造成巨大的经济损失[2-3]。因此，采取措施减轻风振响应的影响成为这类结构设计的关键之一。

调频减振装置主要利用减振装置的自振频率与结构的受控频率相调频时，将结构本身的振动能量转换到调频减振装置上，达到耗散能量、控制结构动力反应的目的[4]。近年来，这类装置已广泛应用于各类高层结构[5-6]和高耸结构[7-8]的风振控制中。对于自立式高耸结构，无论是理论分析[9]还是实测结果[10]均表明，调频减振装置发挥了一定的作用，能够有效抑制自立式高耸结构的风振响应，从而延长结构疲劳寿命。

然而，目前调频减振装置的设计多采用频域或时域内的动力分析方法[11]，与常规自立式高耸结构抗风设计方法不一致。这使得结构工程师无法采用简单的设计软件来进行结构风振控制的计算与分析，这大大限制了调频减振装置在建筑结构中的推广和应用[12]。基于此，许多学者开展了风振控制实用设计方法的研究，提出了一些统一计算理论[11-13]和解析求解方法[14]。但是，这些方法多是针对高层建筑，所涉及的调频减振装置多是圆形或矩形平面，而自立式高耸结构限于自身的几何特点，所用减振装置多为环形，因此设计相应的调频减振装置，并建立其风振控制设计方法具有重要的现实意义。

本文将首先根据自立式高耸结构的几何特点，设计三种调频减振装置，即环形调频质量阻尼器(Ring Shape Tuned Mass Damper, RS-TMD)、环形调谐液体阻尼器(Ring Shape Tuned Liquid Damper, RS-TLD)和环形调谐液柱阻尼器(Ring Shape Tuned Liquid Column Damper, RS-TLCD)，并建立其力学模型，进行RS-TLD的参数分析；随后，基于等效阻尼比和我国规范的抗风设计方法，建立自立式高耸结构风振控制的统一设计方法；最后，通过数值算例，进行风振控制设计，进而编制程序开展非线性时程分析，从而验证所建立方法的实用性和有效性。

1减振装置与计算模型

1.1环形TMD

1.结构；2. TMD外壳；3. 主质量块；4. 橡胶支座； 5. 加劲板；6.阻尼器；21. 上盖板；22. 下盖板； 23. 外挡板；24. 内挡板；31.调节质量块；32. 滑动支点。 图1　一种环形TMD Fig.1 A ring shape tuned mass damper

从TMD调谐的原理可以将TMD分为底部支承型和悬吊摆动型，目前自立式高耸结构中悬吊摆动型的应用较多[15]，本文根据自立式高耸结构的特点，设计一种橡胶支承的环形TMD，如图1所示，该装置主要由外壳、质量块、橡胶支座、加劲板和阻尼器组成。其主要原理是：质量块提供质量，橡胶支座提供TMD的水平刚度，阻尼器提供TMD所需的阻尼，由外壳与加劲板将反力传递给主结构。此处，橡胶支座采用无阻尼的一般支座，阻尼器采用课题组开发的系列粘滞流体阻尼器[16-17]，根据具体设计要求选用。可见，该装置提供质量、刚度与阻尼的部件分离，相互影响较小，受力清晰；通过滑动支点避免了质量块过大的晃动，剔除了该因素对减振效果的影响；通过调节质量块可在安装后根据实际结构的振动特点，调节装置的调谐频率以提高真实减振效果；装置构造简单、制作方便、具有一定实用价值。

假定质量块内径为Rm,1，外径为Rm,2，高度为hm；橡胶隔震支座沿环形质量块均匀对称布置，且各支座水平刚度相等为krub；综合考虑布置空间及对称性进行安装，且各阻尼器性能参数相同，阻尼系数为Cd，阻尼指数为αd。则RS-TMD的各性能参数表示如下：

(1)

kTMD=nkrub

(2)

(3)

α=αd

(4)

式中，ρm为质量块的密度；n,m分别为橡胶支座和阻尼器的数量；βj为第j根阻尼器与运动方向在(-π/2, π/2)之间的夹角；mTMD为TMD质量块的质量；kTMD为TMD运动方向的刚度；CTMD、α分别为运动方向的阻尼系数和阻尼指数。由上式可见，RS-TMD的质量取决于质量块的几何尺寸和材料密度；刚度取决于橡胶支座的数量和刚度；由于阻尼器通常是对称均匀布置的，因此TMD的阻尼系数取决于粘滞阻尼器的数量、阻尼系数和阻尼指数，TMD的阻尼指数由粘滞阻尼器的阻尼指数决定。

1.2环形TLD

考虑自立式高耸结构的特点，TLD的水箱必须为环形截面水箱(图2)，即为环形TLD。其中，调谐液体可采用水、甘油溶液、ZnSO4溶液等液体，同时为提高阻尼可采用增加格栅、分隔板、漂浮物等措施。考虑水箱体型和调谐频率的要求，可以根据计算将多组水箱进行进行组合，以在满足频率要求的同时尽可能地减小外形的不利影响。

1.结构；2. 水箱；3. 调谐液体 图2　环形TLD Fig.2 A Ring shape tuned liquid damper

假设圆环形深水TLD中水的运动是小振幅的，水是不可压缩的理想势流，且不考虑容器侧壁的弹性变形，通过假设水运动的速度势函数使其满足极坐标下的拉普拉斯方程及相应的边界条件，采用半逆解法即可求出相应的速度势函数，同时考虑结构的振动控制中仅用水箱一阶模态，可以得到水箱的晃动频率[15]：

(5)

(6)

(7)

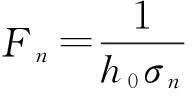
由上述公式可见，RS-TLD的晃动频率主要与水箱截面和水深有关，图3给出了各参数对水箱晃动频率的影响：①图3(a)中令水箱内径为1.24 m，k′在0.5~0.9之间变化，水深在0.3~1.5 m之间变化，由图可见，水箱晃动频率随着k′和水深的增加而升高；②图3(b)中令k′为0.85，水箱内径在0.5~2.5 m之间变化，水深在0.3~1.5 m之间变化，可见随着内径的增加频率降低；③图3(c)中令水深为1 m，k′在0.5~0.9之间变化，水箱内径在0.5~2.5 m之间变化。综上对比可见，在一定参数变化范围内，内径变化对频率的影响程度最大，水深次之，k′影响最小。

图3　各参数对RS-TLD晃动频率的影响 Fig.3 Frequency of RS-TLD changing with variables

1.3环形TLCD

常用的TLCD为U型，由于其底部贯通，对于自立式高耸结构难以适用，本文将两个小型TLCD设置于结构运动方向，两个设置于垂直结构运动方向，如图4所示，管道形状亦可采用矩形截面，通过外壳使它们产生的控制力传递到主结构，称为RS-TLCD。其中，调谐液体可采用水、甘油溶液、ZnSO4溶液等液体，同时为提高阻尼可采用在管道内增加阻尼环等措施。

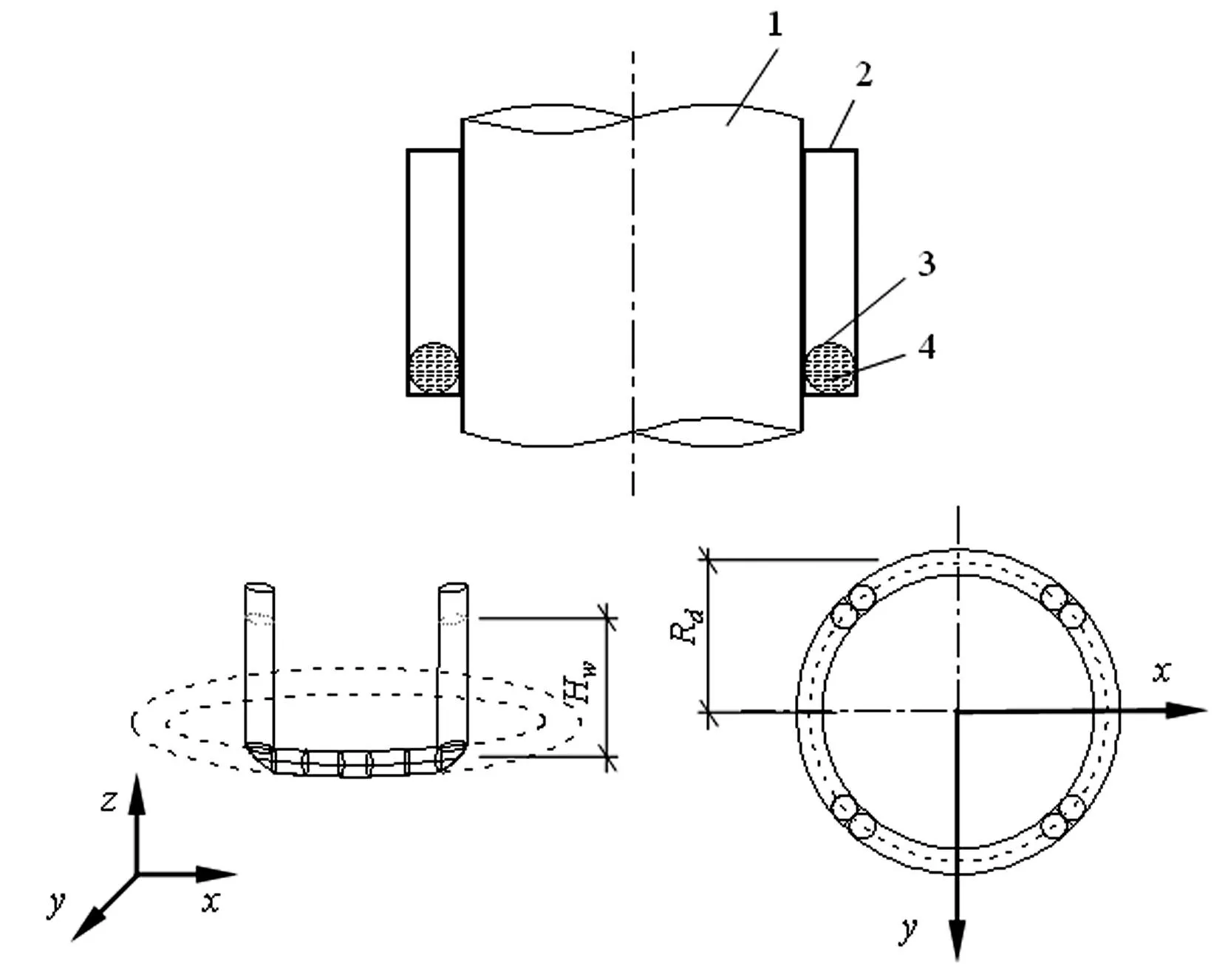
1.结构；2. 外壳；3. 储液管；4. 调谐液体。 图4　一种环形调频液柱阻尼器 Fig.4 A Ring shape tuned liquid column damper

由液柱的动力平衡，可得单个TLCD动力方程[15]：

(8)

(9)

由于整个装置在运动方向上有两个水箱，因此

(10)

式中，ρ为水的密度；A为管状水箱的横截面积；B为水箱竖管的中心距，近似取为(πRd/2-2r)；L为水箱中水中心线的总长度，对于本文的水箱取πRd/2-2r+2Hw；r为水管半径。由上述分析可见，RS-TLCD的调谐频率与其中管道内液体的轴线长度的平方根成反比，而晃动的阻尼比与小孔面积与管道截面积的比值有关。

2风振控制设计方法

2.1结构风振控制的统一方程

分析自立式高耸结构的振动特点[18]，其前四阶归一化振型的最大值均出现在结构顶点，故通常在其顶部设置一个调频减振装置。在动力荷载作用下，设置调频减振装置的自立式高耸结构风振响应可由以下动力方程统一描述[15]：

(11)

(12)

(13)

2.2等效阻尼比的计算

应用振型叠加法对动力方程进行坐标变换可得：

(14)

(15)

式中，fj=ΦjT{P(t)}/Mj，为结构第j振型广义荷载；qj为结构广义位移；fD,j(t)=ΦjT[H]FD/Mj为第j振型的减振装置广义控制力；Mj=ΦTj[M]Φj，为结构第j振型广义质量；ωj为结构第j振型的圆频率；Φji为第j振型第i点的振型值；ζD和ωD分别为减振装置的阻尼比和调谐频率(表1)。将式(13)代入式(14)有：

(16)

表1　调谐减振装置参数表达式

进一步令yD=Φjig，代入式(16)有：

(17)

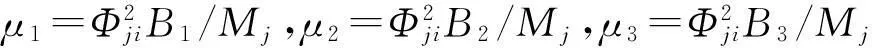
令fj为简谐输入，即fj(t)=eiωt，代入式(17)可得减振结构体系的频响函数为：

(18)

(19)

如此，可应用随机振动的方法，比对未减振结构表达式，得到减振装置对结构的等效阻尼比为：

(20)

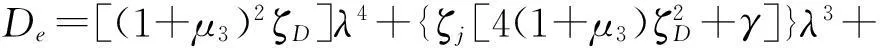
4ζjζDλ+ζD

2.3减振设计流程

在使减振装置的控制效果达到最佳的同时，需考虑减振装置自身行程的限制，因此，寻找其最优参数是十分有必要的。针对自立式高耸结构，其阻尼比远小于一般结构，因此可以忽略结构阻尼比的影响，以简化该问题。尽管如此，寻找减振装置的最优参数仍是一个复杂的有约束优化，为便于设计应用，提出自立式高耸结构调谐减振的实用优化方法，具体流程如图5所示。

图5　自立式高耸结构调谐减振体系设计流程 Fig.5 Design flow chart of tuned absorbers attached to self-standing high-rise structures

(1)分析原结构动力特性与风振响应，根据工程要求选定调谐减振装置种类，并确定模态质量比，通常在0.03~0.08之间。

(2)假定对减振装置的位移没有限制，则仅需令ζj=0，并对减振装置的频率比和阻尼比求偏导，进而联立方程求解，即可求得在无约束条件的情况下，最优减振装置的参数[12]：

ζopt=0.5{γ(1+μ3-0.25γ)/

[(1+μ3)(1+μ3-0.5γ)]}0.5

(21)

λopt=(ωD/ωj)=(1+μ3-0.5γ)0.5/(1+μ3)(22)

(3)将上式算得的结果代入式(20)计算等效阻尼比，并与结构阻尼比相加，采用现行荷载规范方法计算结构荷载，进而由力学分析获得结构和减振装置的风致响应。

(4)比较结构响应和减振装置响应与其限值的大小，若满足限值要求，则设计完成，若不满足，则进行参数更新。更新的原则可根据参数与结果的变化趋势选择，或采用遗传算法等优化设计的方法[15]。得到新参数后，返回第(2)步，如此循环往复直至满足约束条件要求。

(5)得到最终减振参数后，按照第2节的计算模型，结合结构的几何特点，设计减振装置的构造参数。

3风振控制设计算例

3.1工程概况

分别选用高度为50 m和90 m的典型自立式高耸结构进行风振响应分析，结构基本信息见表2。结构1(高度50 m)为建造于我国的一个自立式钢烟囱，高径比为21.7；结构2(高度90 m)为建造于欧洲的一个自立式钢烟囱，高径比达到了39.1。计算时，对于50 m的结构，阻尼比取0.01；90 m的结构，阻尼比取0.003[19]。

表2　结构基本信息

3.2减振装置设计

基于我国规范的相关内容，针对两个算例进行抗风分析和减振设计，根据实际情况分别取模态质量比为0.05和0.08左右，具体数值需根据减振装置特点进行调整，其余参数按照第2节中的设计方法进行设计。设计时，先选择顺风向风振进行设计，而后在横风向进行校核。表3给出了两个算例减振设计的结果，其中RS-TLD中的n为阻尼器个数；RS-TLCD中的n为每层设置n个TLCD，N为设置N组(即N层)，均设置在顶部，阻尼比括号内的数值表示开洞率。分析可见：①对于算例结构，采用RS-TMD、RS-TLD均能取得较好的减振效果，而采用RS-TLCD减振效果较差；②由于需要控制减振装置的行程，因此装置的阻尼比取值相对较大；③对于结构1，RS-TLD的内径仅有0.3 m，几何上无法满足该结构外径的尺寸要求，而结构2的几何设计显然能满足结构尺寸要求，因此， RS-TLD并不是所有自立式高耸结构均适用。

表3　减振装置设计参数

为进一步讨论等效阻尼比方法的有效性，借助自行编制的分析程序[15]，针对结构1顺风向风振响应，分别采用等效阻尼比进行线性时程分析(Equivalent Damping Method, EDM)和直接时程分析方法(Time History Methods, THM)进行分析，并对结果进行对比。由图6可见： ①两种方法得到的计算结果相差不大，因此，可以采用EDM对自立式高耸结构进行减振分析；②功率谱密度曲线中，EDM的曲线仅存在一个极值，而THM的曲线在小阻尼(RS-TLD的情况)时存在两个明显的极值。图7给出了两种方法得到的各减振体系的位移根方差，对比可见：①通过附加减振装置能够较好地衰减结构的动力响应，各类减振体系顶点根方差位移的平均衰减率达25%；②采用RS-TMD、RS-TLD的减振效果相对较好，RS-TLCD的减振效果相对较差，这与通过等效阻尼比得到的结论相一致；③采用EDM与THM得到的结果误差平均为5.37%，满足工程分析的需要，因此可以采用等效阻尼比的方法进行减振设计。

将表3中得到的结构等效阻尼比直接代入规范方法中，即可得到按中国规范设计的结构顶点位移响应峰值(见图8和图9，其中NoD表示未设置任何减振装置的结构)，分析可见：①对于顺风向响应，总的响应在安装阻尼装置后有一定的衰减，结构1平均达到15%以上，最高可达22%，结构2平均超过了40%，最高可达50%，其中由脉动风引起的响应衰减较多，由静力风引起的响应则不会发生改变，减振装置主要控制由脉动风引起的位移；②对于由横风引起的响应，安装减振装置后，结构1平均衰减达60%，最大衰减值达到85%左右，结构2平均衰减达80%，最大衰减值超过了90%；③对比顺风向与横风向的结果可知，由于横风共振主要由固定模态引起，且调谐减振装置主要控制结构的某一模态的振动，调谐减振技术对自立式高耸结构由横风引起的响应具有更好的控制效果；④对比结构1和结构2的结果可知，减振技术对于大长细比、小阻尼的自立式高耸结构具有更好的控制效果。

图6　不同方法顶点位移时程分析结果对比 Fig.6 Comparison between the top displacements by EDM and THM

图7 结构1顶点根方差位移Fig.7VarianceoftheStructure1’stopdisplacements图8 结构1顶点位移响应Fig.8TopdisplacementsoftheStructure1

图9　结构2顶点位移响应 Fig.9 Top displacements of the Structure 2

4结论

针对自立式高耸结构的特点，设计了三种调频阻尼器(RS-TMD、RS-TLD和RS-TLCD)，建立了自立式高耸结构风振控制设计方法，最后，通过数值算例对该方法的实用性和有效性进行了研究，得出以下结论：

(1)所设计的三种调谐减振装置适应于自立式高耸结构的特点，能够有效降低结构的风振响应。进一步的参数分析表明，一定参数变化范围内，RS-TLD内径变化对频率的影响程度最大，水深次之，k′影响最小。

(2)对比了借助等效阻尼比的时程分析和直接通过动力方程的时程分析结果的差异，各减振体系在两种方法下的顶点根方差位移响应相差在5%左右，因此基于等效阻尼比概念的高耸结构风振控制设计方法能够用于自立式高耸结构的风振控制。

(3)对比各减振装置的设计过程和减振效果可知，采用RS-TMD和RS-TLD均能取得较好的减振效果，而采用RS-TLCD减振效果较差；由于尺寸的限制，RS-TLD并不是所有自立式高耸结构均适用，而是更适用于大长细比的自立式高耸结构；减振装置主要用于控制结构的动力响应，且各装置对横风向风振的控制效果均好于对顺风向响应的控制，这对于可能由涡激振动导致破坏的自立式高耸钢结构尤为重要。

参考文献

[1]Roy S, Park Y C, Sause R,et al. Fatigue performance of stiffened pole-to-base plate socket connections in high-mast structures[J]. Journal of Structural Engineering-ASCE, 2012, 138(10): 1203-1213.

[2]Repetto M P, Solari G. Wind-induced fatigue collapse of real slender structures[J]. Engineering Structures, 2010, 32(12): 3888-3898.

[3]CHOU Jui-Sheng, TU Wan-Ting. Failure analysis and risk management of a collapsed large wind turbine tower[J]. Engineering Failure Analysis, 2011, 18(1): 295-313.

[4]李爱群. 工程结构减振控制[M]. 北京: 机械工业出版社, 2007.

[5]唐意, 顾明. 某超高层建筑TMD风振控制分析[J]. 振动与冲击, 2006, 25(2): 16-19.

TANG Yi, GU Ming. Analysis on control of wind induced vibration of a super-tall building with tmd[J]. Journal of Vibration and Shock, 2006, 25(2): 16-19.

[6]李春祥, 熊学玉. 高层钢结构TMDs风振舒适度控制最优参数与简化设计[J]. 振动与冲击, 2002, 21(2): 86-90.

LI Chun-xiang, XIONG Xue-yu.Optimum parameters and simplified design for wind_induced vibration comfort control on tall steel structure with TMDs system[J]. Journal of Vibration and Shock, 21(2): 86-90.

[7]Lu X L, Chen J R. Mitigation of wind-induced response of Shanghai Center Tower by tuned mass damper[J]. Structural Design of Tall and Special Buildings, 2011, 20(4): 435-452.

[8]Lu X L, Chen J R. Parameter optimization and structural design of tuned mass damper for Shanghai centre tower[J]. Structural Design of Tall and Special Buildings, 2011, 20(4): 453-471.

[9]Colwell B, Basu B. Tuned liquid column dampers in offshore wind turbines for structural control[J]. Engineering Structures, 2009, 31(2): 358-368.

[10]Brownjohn J M W, Carden E P, Goddard C R,et al. Real-time performance monitoring of tuned mass damper system for a 183 m reinforced concrete chimney[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010, 98(3): 169-179.

[11]项海帆, 瞿伟廉. 高层建筑风振控制基于规范的实用设计方法[J]. 振动工程学报, 1999, 12(2): 151-156.

XIANG Hai-fan, QU Wei-lian.Practical design method based on design code for controlling wind-induced vibration of tall buildings[J]. Journal of Vibration Engineering, 1999, 12(2): 151-156.

[12]瞿伟廉, 陶牟华, Chang C C. 五种被动动力减振器对高层建筑脉动风振反应控制的实用设计方法[J]. 建筑结构学报, 2001(02): 29-34.

QU Wei-lian, TAO Mu-hua, Chang C C. Practical design method for effect of five kinds of passive dynamic absorbers on fluctuation wind-induced vibration response control of tall buildings[J]. Journal of Building Structures, 2001,22(2): 29-34.

[13]吕明云, 瞿伟廉. 非线性被动动力减振器对高耸结构风振控制的实用设计方法[J]. 振动与冲击, 2004, 23(1): 27-29.

LÜ Ming-yun, QU Wei-lian.Practical method of designing nonlinear passive dynamic absorbers for wind-induced vibration control of highrise structure based on chinese code[J]. Journal of Vibration and Shock, 2004, 23(1): 27-29.

[14]李创第, 葛新广, 朱倍权. 带五种被动减振器的高层建筑基于Davenport谱随机风振响应的解析解法[J]. 工程力学, 2009(4): 144-152.

LI Chuang-di, GE Xin-guang, ZHU, Bei-quan. Exact analytic method for random wind-induced response of tall building structures with five sorts of passive dampers on the basis of davenport spectrum[J]. Engineering Mechanics, 2009(4): 144-152.

[15]陈鑫. 高耸钢烟囱风振控制理论与试验研究[D]. 南京: 东南大学, 2012.

[16]黄镇, 李爱群, 刘康安,等. 螺旋孔式粘滞阻尼器： 中国， CN101555922[P] 2009年10月14日.

[17]李爱群, 黄镇, 刘康安,等. 可控式粘滞阻尼器： 中国， CN101576139[P] 2009年11月11日.

[18]陈鑫, 李爱群, 程文瀼,等. 高耸结构动力特性分析的Adomian分解法[J]. 振动工程学报, 2013, 26(4): 493-499.

CHEN Xin, LI Ai-qun, CHENG Wen-rang, et al.Study on dynamic characteristics of high-rise buildings based on Adomian decomposition method[J]. Journal of Vibration Engineering, 2013, 26(4): 493-499.

[19]陈鑫，李爱群，王泳,等. 国内外规范自立式高耸结构等效风荷载及响应比较[J]. 建筑结构学报, 2014, 35(4): 304-311.

CHEN Xin，LI Ai-qun，WANG Yong, et al. Comparative study on equivelent wind loads and dynamic responses of self-standing high-rise structures in different codes[J]. Journal of Building Structures, 2014, 35(4): 304-311.