结构减震的稳定时滞LSSVM-LQR智能控制算法

第一作者李春祥男，教授，博士生导师，1964年12月生

结构减震的稳定时滞LSSVM-LQR智能控制算法

李春祥1,赵德奇2,蓝声宁1

(1.上海大学土木工程系，上海200072; 2.上海工程勘察设计有限公司，上海200050)

摘要：针对时滞LSSVM-LQR智能控制算法存在的稳定性问题，提出相关的稳定性控制算法，以确保时滞LSSVM-LQR智能控制算法的鲁棒性。该算法的主要思路为：在时滞LSSVM-LQR控制算法中，加入控制力限制条件。当满足控制力限制条件时，控制程序继续运行；当不满足控制力限制条件时，控制程序自动跳出，便执行稳定性控制算法(或称为稳定/鲁棒的时滞LSSVM-LQR智能控制算法)。稳定性控制算法主要是通过调整反馈来控制作动器运行，从而确保控制系统的稳定性。数值结果表明，稳定性控制算法能够有效地保证时滞LSSVM-LQR智能控制算法的稳定性/鲁棒性；与时滞LSSVM-LQR智能控制算法相辅相成。

关键词：智能控制算法；时滞；LSSVM-LQR；稳定性；地震

基金项目：湖南省教育厅资助项目(11C0549)

收稿日期：2013-04-09修改稿收到日期：2013-11-06

中图分类号:TU311

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.07.018

Abstract:Aiming at the stability problem of the LSSVM-LQR intelligent control algorithm for reducing seismic responses of structures, a stability controlling algorithm was proposed to ensure good robustness of the LSSVM-LQR intelligent control algorithm. The main idea of this algorithm is that the limition of control forces is imposed on the control algorithm. If the limition condition of control forces is fulfilled, the control procedure continues to run. However, if the limitation condition of control forces is not fulfilled, the control procedure automatically jumps out and then, instead, the stability controlling algorithm starts to be applied. The whole procedure was referred to as the stable/robust LSSVM-LQR intelligent control algorithm, which ensures the stability of the system mainly through controlling actuator operation with resorting to adjusting feedback. The numerical results show that the developed stability controlling algorithm can effectively guarantee the stability/robustness of LSSVM-LQR intelligent control algorithm. The time-delay LSSVM-LQR intelligent control algorithm and the stability/robust time-delay LSSVM-LQR intelligent control algorithm can complement each other in application.

Robust LSSVM-LQR based time-delay intelligent control algorithm for reducing seismic responses of structures

LIChun-xiang1,ZHAODe-qi2,LANSheng-ning1(1.Department of Civil Engineering，Shanghai University，Shanghai 200072,China;2.Shanghai Architectural and Engineering Consultants Co., Ltd., Shanghai 200050, China)

Key words:intelligent control algorithms; time-delay; LSSVM-LQR; stability; earthquakes

时滞往往使主动控制系统的控制效果大大减弱；甚至系统存在不稳定的可能。解决时滞问题的主要方法为时滞补偿方法。到目前为止，国内外学者通过对时滞研究，提出了众多的时滞补偿方法，归纳起来大致可以分为三种类型：理论性补偿[1-4]、相空间补偿[5-7]、时域补偿[8]。尽管如此，时滞补偿主动控制系统仍然存在稳定性问题，即在外界干扰后，原处于平衡状态的时滞补偿主动控制系统出现振荡发散现象。因此，稳定性分析仍然是时滞补偿主动控制器设计的重要内容。因此，虽然文献[9]提出的时滞LSSVM-LQR智能控制算法能够有效地降低时滞对结构主动控制系统的不利影响，但有必要检验该算法的稳定性。鉴于此，本文将研究基于LSSVM-LQR结构地震响应时滞智能控制算法的稳定性，并给出相应的解决方法，建立稳定/鲁棒的时滞LSSVM-LQR智能控制算法。

1时滞LSSVM-LQR智能控制算法存在的稳定性问题

时滞LSSVM-LQR智能控制算法为一种时域补偿算法，是通过预估位移和速度来进行时滞补偿。当时滞时间较长时，因预测状态与无时滞状态有较大的出入，导致补偿效果较差，甚至出现负效应。一旦这种负效应出现积累，则结构振动将出现发散现象，即出现不稳定情况。

图1　时滞为0.3 s的三种控制算法，在El Centro波作用下结构响应和控制力 Fig.1 Employing three control algorithms with time delay 0.3 s, responses of the structure and control forces under El Centro wave

图2　时滞为0.3 s的三种控制算法，在Loma prieta波作用下结构响应和控制力 Fig.2 Employing three control algorithms with time delay 0.3 s, responses of the structure and control forces under Loma prieta wave

图1~4给出了对于时滞为0.3 s的三种控制算法，在四种地震波作用下结构位移、加速度以及控制力时程曲线。从图1~4可以看出，对于时滞LSSVM-LQR智能控制算法，当时滞为0.3 s时，在El Centro波、Loma prieta波、Taft波三条波作用下，结构响应和控制力时程开始产生发散现象,在上海人工波1作用下，结构响应和控制力时程尚未产生发散现象，还具有一定的控制效果,然而，若时滞时间继续加长，上海人工波1终究也会导致结构响应和控制力时程的发散。因此，如何对时滞LSSVM-LQR智能控制算法进行稳定性控制直接关系到时滞LSSVM-LQR智能控制算法实现的成败。

图3　时滞为0.3 s的三种控制算法，在Taft波作用下结构响应和控制力 Fig.3 Employing three control algorithms with time delay 0.3 s, responses of the structure and control forces under Taft wave

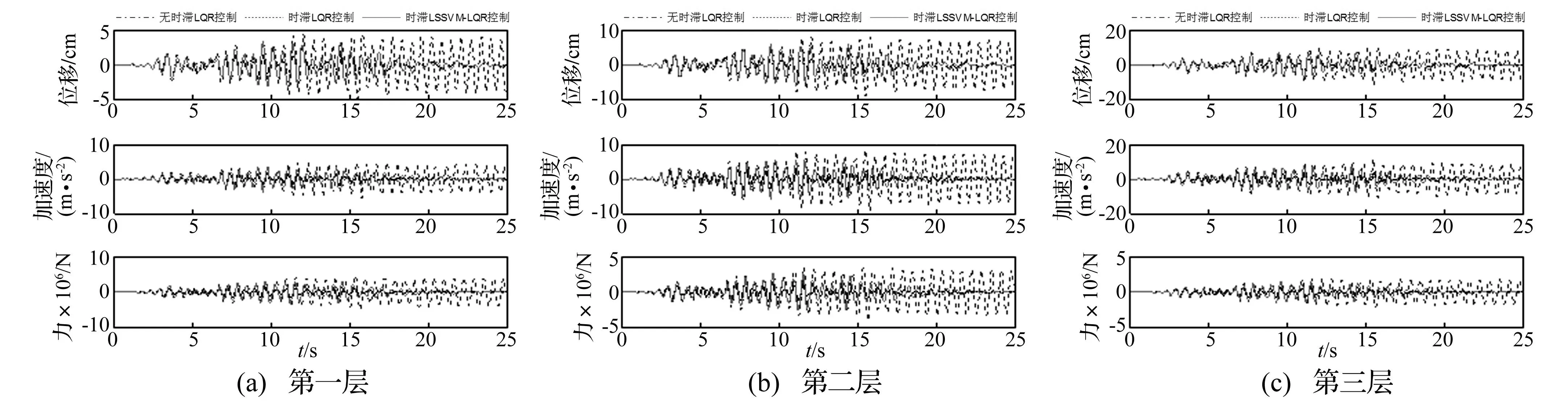
图4　时滞为0.3 s的三种控制算法，在上海人工波1作用下结构响应和控制力 Fig.4 Employing three control algorithms with time delay 0.3 s, responses of the structure and control forces under Shanghai artificial wave1

2时滞LSSVM-LQR智能控制算法的稳定性算法

2.1稳定性算法流程

稳定性控制算法的思路为：在时滞LSSVM-LQR智能控制算法中，加入控制力限制条件。当满足控制力限制条件时，程序继续运行；当不满足控制力限制条件时，控制程序自动跳出，便执行以下的稳定性控制算法(或称为稳定/鲁棒的时滞LSSVM-LQR智能控制算法)。

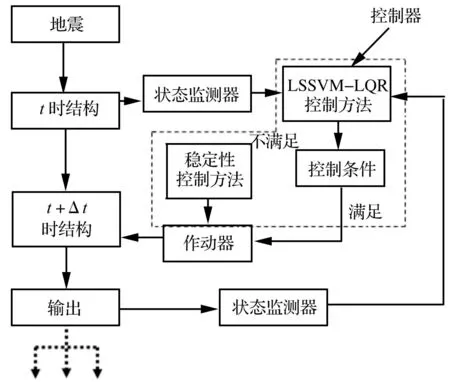
图5　时滞LSSVM-LQR智能控制算法的稳定性算法流程 Fig.5 Stable algorithm flowchart of the time-delay LSSVM-LQR intelligent control algorithm

2.2稳定性算法

LSSVM-LQR控制系统的离散状态方程可表示为：

(1)

设Y(k)=BdGZ′(k)，并将Z(k+1)和Y(k)按位移和速度展开：

(2)

图6　时滞LSSVM-LQR智能控制 算法的稳定性算法程序 Fig.6 Block flow diagram of stable algorithm in the LSSVM-LQR intelligent control algorithm

并设

X=X1(k+1)+

X2(k+1)+

X3(k+1)

(3)

Y=Y1(k)+

Y2(k)+Y3(k)

(4)

于是，稳定性控制算法的思路为：当X与Y同号时，按时滞LSSVM-LQR智能控制算法算得的最优控制力进行直接反馈；若为异号，则将算得的最优控制力加上负号替代按时滞LSSVM-LQR算法算得的最优控制力进行反馈。稳定性控制算法程序框图如图6所示。

由图5~6知，本文所提出的“控制力反向替代最优控制力进行反馈”准则，对所有控制形式均满足，即只要不满足控制力条件：U′<αUmax，都需要按“控制力反向替代最优控制力进行反馈”的准则进行反馈。

3稳定/鲁棒的时滞LSSVM-LQR智能控制算法数值验证

继续采用文献[9]的三层剪切型框架结构为例，来进行稳定/鲁棒的时滞LSSVM-LQR智能控制算法数值验证。由于相应于ElCentro波、Lomaprieta波、Taft波、上海人工波1的控制力大小不同，所以在采用稳定性控制程序时对控制条件进行了差别处理，具体确定的控制条件如表1所示。根据图5~6和表1的控制条件，分别对四条波作用下的结构进行了稳定性控制，以数值验证本文稳定性算法的可行性。为了比较，依然选择时滞为0.3s的无时滞LQR控制、时滞LQR控制和稳定/鲁棒的时滞LSSVM-LQR智能控制算法，结构响应和控制力时程曲线如图7~10所示。

表1　稳定/鲁棒的时滞LSSVM-LQR智能

控制算法的控制力限制条件

Tab.1 Control forcerestrictions in the stable/robust

LSSVM-LQR intelligent control algorithm

图8　时滞为0.3 s稳定时滞LSSVM-LQR智能控制算法，在Loma prieta波作用下结构响应和控制力 Fig.8 Employing robust time delay LSSVM-LQR control algorithm with time delay 0.3 s, responses of the structure and control forces under Loma prieta wave

对比分析图1~4和图7~10，得主要结论：

(1)当采用稳定/鲁棒的时滞LSSVM-LQR智能控制算法后，结构位移、加速度以及控制力时程的发散现象消失。因此，稳定/鲁棒的时滞LSSVM-LQR智能控制算法可以确保结构响应和控制力的稳定。

(2)当采用稳定/鲁棒的时滞LSSVM-LQR智能控制算法后，原先收敛的结构响应和控制力继续保持收敛，能保证较好控制性能的延续。然而，我们不能因此而否决时滞LSSVM-LQR智能控制算法的有效性。经数值比较，平均上，图10的第二层峰值位移较单独采用时滞LSSVM-LQR智能控制算法的图4第二层峰值位移大9.5%，峰值加速度大13.2%，最大控制力大12.4%。因此，稳定/鲁棒的时滞LSSVM-LQR智能控制算法与时滞LSSVM-LQR智能控制算法并不冲突，而是相互发挥各自优势。

图9　时滞为0.3 s稳定时滞LSSVM-LQR智能控制算法，在Taft波作用下结构响应和控制力 Fig.9 Employing robust time delay LSSVM-LQR control algorithm with time delay 0.3 s, responses of the structure and control forces under Taft wave

图10　时滞为0.3 s稳定时滞LSSVM-LQR智能控制算法，在上海人工波1作用下结构响应和控制力 Fig.10 Employing robust time delay LSSVM-LQR control algorithm with time delay 0.3 s, responses of the structure and control forces under Shanghai artificial wave1

表2　当时滞LSSVM-LQR智能控制算法跳出时的

(3)从图7~图10，虽然稳定/鲁棒的时滞LSSVM-LQR智能控制算法可以保证结构的稳定性，但其整体控制效果较无时滞控制差很多，已不具备时滞LSSVM-LQR智能控制算法的优越性。

(4)表2给出在不满足控制力限制条件时，跳出时滞LSSVM-LQR智能控制算法所对应的循环步及对应走过的时长。从图7~图10看出，在跳出时滞LSSVM-LQR智能控制算法之前时间段，时滞LQR控制算法下结构响应尚未发散，三种控制算法下的曲线较为重叠；而在跳出时滞LSSVM-LQR智能控制算法之后时间段，时滞LQR控制算法控制下结构响应逐渐发散，三种控制下的曲线重合度较差，说明跳出点较为恰当，稳定性控制算法较为符合实际控制情况。

(5)为数值验证稳定性控制算法的有效性，选取了不同的控制力限值。程序验证表明，当选取的控制力限值较小时，控制较早地由时滞LSSVM-LQR智能控制算法跳入到稳定/鲁棒的时滞LSSVM-LQR智能控制算法中；当选取的控制力限值较大时，控制较晚地由时滞LSSVM-LQR智能控制算法跳入到稳定/鲁棒的时滞LSSVM-LQR智能控制算法中。显然，控制力限值的选取很重要，当时滞影响较小时，控制力数值尚未达到控制力限值，程序将不会跳出时滞LSSVM-LQR智能控制算法；反之，则跳出。因此，这种控制实现可以使得两种控制模式相得益彰、相辅相成。

4结论

针对时滞较长时，时滞LSSVM-LQR智能控制算法出现控制发散现象，提出了稳定/鲁棒的时滞LSSVM-LQR智能控制算法。核心技术为：在时滞LSSVM-LQR智能控制算法中，植入控制力限制条件,当满足控制力限制条件时，程序继续运行；当不满足控制力限制条件时，程序自动跳出，执行稳定/鲁棒的时滞LSSVM-LQR智能控制算法。数值结果表明，稳定/鲁棒的时滞LSSVM-LQR智能控制算法与时滞LSSVM-LQR智能控制算法相辅相成。

本文修正算法仅仅是对文献[9]算法的一种修正，是基于作动器控制力大小给出的修正，目标是提高系统的鲁棒性。因此, 该修正算法的适用性不受时滞大小而限制。从结论的第二条可知，修正算法并不优于文献[9]算法。修正算法的核心思想: 对文献[9]算法施加一种约束，以最大程度地发挥其核心算法。也可以说，修正算法的优越性体现在文献[9]算法上，是其算法的一种补充。具体地，综合本文计算和文献[9]可知，在时滞0.2s内时即10个反馈步以内时，实际运用价值很高；在时滞大于0.2s时即大于10个反馈步时，修正算法可保证系统的稳定性。

参考文献

[1]Hammarstrom L G, Gros K S. Adaptation of optimal control theory to systems with time delay [J]. International Journal of Control, 1980, 32(2): 329-357.

[2]Lin Chi-chang, Chang Chang-ching, Chen Huang-lin. OptimalH∞output feedback control systems with time delay [J]. Journal of Engineering Mechanics, 2006,132 (10): 1096-1105.

[3]蔡国平，黄金枝. 控制存在时滞的线性系统主动控制的滑移模态方法[J]. 力学季刊，2002，23(2): 164-172.

CAI Guo-ping, HUANG Jin-zhi. Sliding-mode control method for linear systems with time-delay in control[J]. Chinese Quarterly of Mechanics, 2002，23(2): 164-172.

[4]潘颖，王超，蔡国平. 线性时滞系统的离散最优控制[J]. 计算力学学报，2004，21(2): 177-184.

PAN Ying, WANG Chao,CAI Guo-ping. Discrete-time optimal control method for linear time-delay systems. Chinese Journal of Computational Mechanics，2004，21(2): 177-184.

[5]Chung L L, Lin R C, Soong T T, et al. Experimental study of active control for MDOF seismic structures [J]. Journal of Engineering Mechanics, 1989, 115(8): 1609-1627.

[6]代晶辉，刘军龙，张春巍，等. 部分状态反馈的主动利用时滞补偿方法[J] 振动工程学报,2011，24(3)：246-252.

DAI Jing-hui, LIU Jun-long, ZHANG Chun-wei, et al. Time delay compensation method based on partial state feedback and active increasing time delays[J]. Journal of Vibration Engineering, 2011，24(3)：246-252.

[7]刘军龙，代晶辉，张春巍，等. 基于位移反馈控制的主动增加时滞补偿方法及其试验验证[J]. 振动与冲击, 2011，30(6)：185-191.

LIU Jun-long, DAI Jing-hui, ZHANG Chun-wei, et al. Time delay compensation method based on displacement feedback and active increasing of time delay and its experiment verification[J]. Journal of Vibration and Shock, 2011, 30(6): 185-191.

[8]Abdel-Rohman M. Time-delay effects on active damped structures[J]. Journal of Engineering Mechanics, 1987, 113(11): 1709-1719.

[9]赵德奇，李春祥，蓝声宁. 基于最小二乘支持向量机的结构地震响应时滞控制算法[J]. 振动与冲击，2013, 32(9): 165-172.

ZHAO De-qi, LI Chun-xiang, LAN Sheng-ning. Least squares support vector machine based time-delay control algorithm for reducing seismic responses of structures[J]. Journal of Vibration and Shock, 2013, 32(9): 165-172.