电动车减/差速器振动特性分析及改进

第一作者于蓬男，博士生，1986年生

通信作者章桐男，教授,博士生导师，1960年生

电动车减/差速器振动特性分析及改进

于蓬1,2,章桐1,2,3,冷毅1,2,郭荣1,2

(1.同济大学新能源汽车工程中心，2.同济大学汽车学院，3.同济大学中德学院，上海201804)

摘要：以某纯电动车的减/差速器为研究对象，首先考虑齿轮啮合刚度、传动误差、齿侧间隙和轴承因素，建立了齿轮传动系模型；然后考虑传动轴、差速器壳体以及减速器壳体的柔性，建立了减/差速器系统综合耦合模型，对其进行动态响应仿真分析及试验验证；最后通过轮齿微观修形减小齿轮传递误差波动的幅值，降低壳体表面阶次振动的峰值。结果表明，所建立的综合耦合模型能较好的预测减/差速器系统的振动特性，揭示各个振动阶次产生的原因，轮齿修形可使齿轮副传递误差波动幅值和壳体表面阶次振动峰值分别降低40%和57%，对减/差速器啸叫问题的解决起到一定的积极作用。

关键词：电动车；减/差速器；有限元；转鼓试验；轮齿修形

基金项目：国家863计划项目(2011AA11A265);国家自然科学基金(51205290);中央高校基本科研业务费专项资金项目(1700219118)

收稿日期：2014-09-24修改稿收到日期：2014-12-03

中图分类号:U469.72+2

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.07.014

Abstract:Targeting the improvement of the differential/reducer of electric vehicle, a bending-torsion-axial motion-swinging coupled gear train analysis model was built, in consideration of the effects of gear meshing stiffness, transmission errors, backlash and bearing factors. Then, an integrated coupled model of differential/reducer system considering the flexibility of shaft, differential housing and gearbox housing was established, and the dynamic response simulation analysis and experimental verification were conducted. Gear teeth modifications were carried out to reduce the amplitude of transmission error，as well as the order vibration of power train shell surface. The results show that the integrated coupled model can predict the vibration characteristics of the differential/reducer system effectively and reveal the resource of each vibration order. The teeth modification can reduce the amplitude of transmission error and the order vibration peak of shell surface by 40% and 57%, respectively, which provides a positive effect to resolve the problem of differential/reducer whine.

Vibration characteristics analysisand improvement of differential/reducer of electric vehicle

YUPeng1,2,ZHANGTong1,2,3,LENGYi1,2,GUORong1,2(1. New Clean Energy Automotive Engineering Center, Tongji University, Shanghai 201804, China;2. School of Automotive Studies, Tongji University, Shanghai 201804, China;3. Sino-German College of Applied Sciences，Tongji University，Shanghai 201804,China)

Key words:electric vehicle; differential/reducer; finite element; dynamometer test; gear teeth modification

集中式驱动电动车存在两类明显的高阶次噪声，电机啸叫噪声和减/差速器啸叫噪声，着眼于后者进行研究。电动车用减/差速器往往采用固定速比传动，造成多数齿轮在重载荷条件下工作，其转速范围也远高于传统内燃机车辆的变速箱，在几种车型的消声室噪声试验中发现，电动车减/差速器的敲击噪声较小而啸叫噪声明显；齿轮系统在传动过程中受到各种动态激励的影响产生啮合振动，这些振动依次传递至传动轴、轴承和壳体，引发壳体共振，对外辐射噪声；因此有必要对减/差速器的振动特性进行深入研究，为电动车的NVH性能评估及改进提供指导。文献[1-7]以各类船用、内燃机车用、特种用变速器为研究对象，考虑齿轮传动系各激励，包括误差激励[1-7]、刚度激励[1-7]、冲击激励[4,7]、轴承时变刚度和阻尼[5,7]，搭建齿轮箱有限元模型,进行振动特性分析[1-7]；文献[8-10]以电动车用减/差速器为研究对象，进行了传动系统振动特性仿真、变速器箱体模态仿真及模态试验研究；但目前已有研究中，以电动车用减/差速器为研究对象，添加各种动态啮合激励，全面考虑必要部件柔性的影响，搭建综合耦合模型，并将动响应仿真和整车转鼓试验相结合的方法进行系统研究的文献较少。

本文结合工程实际，在前期研究的基础上，对某款集中式驱动纯电动车用减/差速器的振动特性进行系统分析及改进。针对减/差速器的啸叫现象，在齿轮传动系统刚性模型的基础上，搭建能准确预测振动阶次特性的多柔性综合耦合模型，全面把握其振动的阶次、频率范围及幅值特性，并用试验验证综合模型正确性，最后通过轮齿微观修形对传递误差和系统振动响应进行优化，为该款电动车用减/差速器的减振降噪提供理论依据。

1齿轮啮合理论模型

所研究的减/差速器为斜齿圆柱齿轮传动，考虑传动轴、支承等的弹性变形，齿轮系统将具有弯曲振动、扭转振动、轴向振动以及因轴向动态啮合分力产生的扭摆振动。为简化计，用相对于齿轮对称布置的支承弹簧模拟传动轴及支承的横向弯曲弹性，得到齿轮副啮合振动理论模型如图1示。

图1　齿轮副弯-扭-轴-摆分析模型 Fig.1 Bending-torsion-axle-swing analysis model

图1所示为三维空间的8自由度振动系统，其广义位移列阵{δ}可表示为：

{δ}={ypzpθpzθpxygzgθgzθgx}T

(1)

式中，yi，zi(i=p,g)为主、被动齿轮中心点Op和Og在y向和z向的平移振动位移；θix(i=p,g)为主、被动齿轮中心点通过该中心并平行于x轴的轴线的扭摆振动位移；θiz(i=p,g)为主、被动齿轮绕传动轴轴线的扭转振动位移，可推得系统的分析模型为：

(2)

式中，Rpp，Rgp分别为主、被动齿轮的节圆半径；cθix、kθix(i=p,g)分别为主、被动齿轮相应于扭摆自由度的阻尼系数、刚度系数；Ti(i=p,g)为作用在主、被动齿轮上的外载荷力矩。将动态啮合力的切向分力和轴向分力代入上述各式，分析模型可写成如下矩阵形式：

(3)

式中，[m]为质量矩阵，[c]为阻尼矩阵，[k]为刚度矩阵，{P0}为未考虑齿轮啮合刚度及啮合传递误差影响的载荷列阵。

2减/差速器刚性轴齿轮系仿真模型

2.1齿轮系结构组成

电动车减/差速器有别于内燃机变速箱：无离合器、扭转减振器、与驱动电机直接耦合；同时由于电机优越的转矩性能，往往采用单一速比，但这种集成方式对电动车用减/差速器的性能提出了更高的要求[11-12]。图2为所研究电动车减/差速器齿轮传动系的结构简图。齿轮1-4 为渐开线斜齿圆柱齿轮，齿轮5-8为直齿锥齿轮，动力传递路径为：电动机输出-小齿轮1-大齿轮2-中间轴小齿轮3-齿圈4-差速器壳体11-行星齿轮5/6-左右半轴齿轮7/8，再通过半轴传递动力到车轮。

图2　减/差速器齿轮传动系结构简图 Fig.2 Structure diagram of differential/reducer

2.2刚性轴齿轮系Romax仿真模型

使用专业的齿轮系统分析软件Romax进行传动系统建模。首先根据模型实际参数，依次完成轴系建模、齿轮建模、行星齿轮系建模以及定义功率流等步骤；然后为齿轮定义加工精度、表面粗糙度、变位系数和质量等级等参数；从轴承数据库中选择轴承，并设置系统材料和润滑条件等。最终建立包括两级齿轮减速和差速器在内的减/差速器齿轮传动系仿真模型[13]，如图3所示。

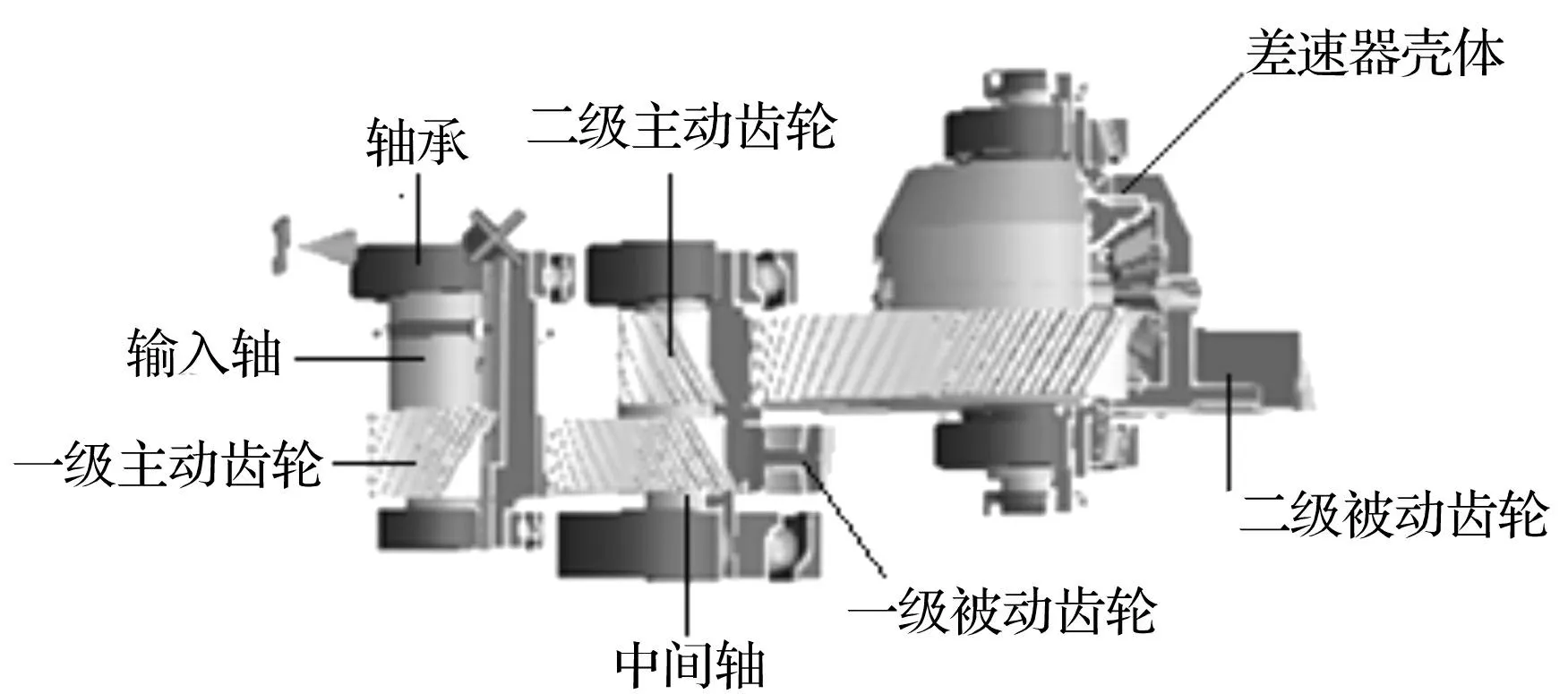
图3　减/速器齿轮传动系模型(刚性轴系) Fig.3 3D model of gear train(rigid shafts)

3减/差速器多柔性综合仿真模型

3.1轴系及差速器壳体的柔性化

图3所示的齿轮系模型有助于研究齿轮啮合、传动误差、齿侧间隙和轴承对齿轮系统的影响，而进一步考虑齿轮系的各传动轴、差速器壳体的柔性特征可以更加准确的预测齿轮系统的振动特性。在前述模型的基础上，考虑必要部件的柔性，将传动轴及差速器壳体进行柔性化。在齿轮系模型界面下，在各部件的工作表属性中选择将轴转化为有限元轴，然后依次完成划分网格、连接节点、缩聚有限元等步骤，实现轴/壳的柔性化。传动轴和差速器壳体柔性化完毕的齿轮系模型如图4所示。

图4　减/速器齿轮传动系模型(柔性轴系) Fig.4 3D model of gear train(flexible shafts)

3.2减速器壳体有限元模型的添加

图5　减/差速器综合耦合模型 Fig.5 Flexible coupling model of differential/reducer

对减/差速器进行故障诊断时，用于测量的加速度传感器往往加装在减速器外壳体上，其柔性特征对整个系统的结构振动和声辐射将产生重要影响[2,4,5,7-9]。将减速器壳体柔性化，可以将仿真与试验结果进行对比，验证模型的正确性。故将经过前处理的壳体有限元模型导入Romax中，通过装配、连接节点和缩聚刚度和质量矩阵等，建立同时考虑轴系柔性、差速器壳体柔性和减速器壳体柔性的多柔性综合耦合模型，如图5所示。减/速器壳体有限元模型实体网格采用四面体划分，厚度较小的部分采用壳单元，刚柔节点用RBE2连接。边界条件设置方面，因悬置系统的频率范围较低(远低于100 Hz)，对减/差速器壳体振动特性的影响较小，将壳体与悬置连接处表面上的节点进行全约束。

4减/差速器振动特性仿真

4.1齿轮系统内部激励

齿轮系统在工作时，会受到外部激励和内部激励的综合作用。外部激励是由于原动机/负载波动、装配偏心等外部因素产生的动态激励；内部激励是由于时变啮合刚度、齿轮误差、轮齿弹性变形等引起的轮齿动态激励。其中，内部激励是所研究齿轮系统动态激励的主要部分，即使不存在外部激励或外部激励为常值，齿轮系统也会在内部激励的作用下产生振动。本文着重分析齿轮传动系统本身结构特性引发的内部激励对动态响应的影响。

使用Romax进行振动特性分析，可以考虑齿轮啮合综合刚度k′和传动误差e等内部激励的综合影响。齿轮副啮合动力学方程(3)右侧的激励项{P0}变为{p}，{p}为考虑齿轮啮合刚度及啮合传递误差影响的载荷列阵。

{p}={P0}+[k′]{e}

(4)

式中，[k′]为啮合综合刚度矩阵，{e}为传动误差载荷列阵。

齿轮啮合刚度k′和传递误差e可在Romax中直接算出，联立(3)、(4)，即得到一对啮合齿轮副的动响应结果。Romax基于齿轮副啮合理论，综合考虑每对齿轮副啮合的结果，可以最终综合得到整个齿轮传动系统的动态响应结果。

在进行动态分析前应先做静态分析，对齿轮、轴、轴承进行强度和可靠性校核，保证系统安全可靠。经验证，所搭建模型的各部件安全可靠。仿真中取电机额定转速2 800 r/min为输入轴转速，输入扭矩12 Nm，持续时间5 h，在Dynamics模块下分别对齿轮系模型和考虑多柔性的综合耦合模型进行动力学求解，并对其振动特性进行对比与分析。

4.2固有特性对比分析

对图3所示齿轮系仿真模型、图5所示减/差速器综合耦合模型进行模态分析，获得6 500 Hz以内的固有频率如表1所示。为便于结果分析和诊断，同时对减速器组件进行模态试验，如图6所示。

表1　齿轮传动系与综合耦合模型固有频率值

图6　减速器模态试验 Fig.6 Modal test of reducer

分析表1(齿轮传动系模态信息用浅灰色标出，减速器壳体模态信息用深灰色标出，轴系柔性引起的模态用斜体标出，耦合作用引起的高频模态信息用加粗数字标出)可知：

(1)齿轮系固有频率(对应图3所示的刚性传动系统)模态分析得到的前21阶齿轮系固有频率普遍高于耦合模型固有频率(对应图5所示的多柔性模型)的结果，原因是前者是将轴承固定于空间点，而后者是将轴承固定于柔性减速器壳体。约束刚度减小使模态值普遍下降，很显然，考虑柔性壳体的约束方式更贴近实际，否则将夸大实际约束情况。

(2)耦合模型固有频率结果中包含了柔性减速器壳体的模态信息，与减速器壳体固有频率结果吻合的较好，若只进行壳体仿真而忽略传动系统及轴承的支撑作用，则无法获得与试验值接近的壳体模态信息。与文献[7]的描述一致，体现了综合耦合模型的有效性。

(3)耦合模型由于考虑了输入轴、中间轴及差速器壳体的柔性，可以获得更丰富的模态信息(斜体数字所示)，而单纯考虑刚性传动系统无法获得全面的仿真结果，不利于减/差速器的测试分析和故障诊断。

(4)5 760 Hz、6 200 Hz两个频率值既与齿轮系的20、21阶结果贴合，又与壳体试验的14、16阶结果接近。可能是由于齿轮传动系、减速器壳体以及相关部件的耦合作用共同引起，应引起足够重视。

4.3齿轮传递误差分析

齿轮啮合力的变化主要取决于内部激励，而传递误差是齿轮啮合过程中重要的内部激励。通过获取和分析传递误差可以预测齿轮系的振动情况。通过动力学求解获得两级齿轮啮合的传递误差。图6、图7分别为一级、二级齿轮啮合传递误差曲线。

由图6可知，齿轮传动系模型一级齿轮传动误差围绕均值1.21 μm上下均匀波动，波动幅度为0.34 μm；而多柔性耦合模型一级齿轮传递误差围绕均值1.14 μm上下均匀波动，波动幅度为0.39 μm。相比而言，耦合模型的一级齿轮传动误差虽然均值减小，但是振幅较大。这是由于考虑了柔性部件的减差速器耦合模型可看作是一个约束变化的斜齿轮副弯-扭-轴-摆耦合模型。壳体和支承系统的弹性，使系统的弯曲、扭转、轴向和扭摆振动形态发生变化，对齿轮副的传递误差和正确啮合产生了一定的影响，表现为齿轮传递误差波动幅值和啮合动态激励有一定程度的加大。从图7看，二级传递误差与齿轮系模型相比变化不大。因此在进行减/差速器系统的仿真、测试及分析时应该更加关注一级齿轮啮合处的振动情况，这为后续优化中的修行齿轮选择提供了依据。

图6 一级齿轮啮合的传递误差Fig.6Transmissionerrorof1stgearmeshing图7 二级齿轮啮合传递误差Fig.7Transmissionerrorof2thgearmeshing图8 轴承6频响曲线Fig.8Frequencyresonanceofbearing6

4.4轴承频响特性分析

求解在齿轮副单位位移激励下的各轴承振动响应曲线，以输出端轴承6为例，其频响特性曲线如图8所示。

由图8可以看出，对于齿轮系模型来说，轴承6的频率响应分别在1 131 Hz、4 202 Hz、6 222 Hz处出现峰值，在频率6 222 Hz处出现最大峰值；对于多柔性耦合模型而言，轴承6频率响应的极值频率有所增加，4 000 Hz和6 000 Hz左右的双峰值则体现了更丰富的振动现象。原因是耦合模型的模态密度大于齿轮系模型，发生共振的频率也有所增多，能更全面的预测系统的振动现象。

4.5壳体节点动态响应仿真

以计算出的一级、二级齿轮副传递误差为激励，可得到各轴承以及各个感兴趣测点随输入轴转速变化的动载荷或动位移响应瀑布图。以壳体上两个仿真测点为例进行说明，如图9所示。

两个测点分别为输入轴1端部对应的测点1、轴承6附近的测点2。仿真完成后，提取测点的振动响应结果如图10、图11所示。

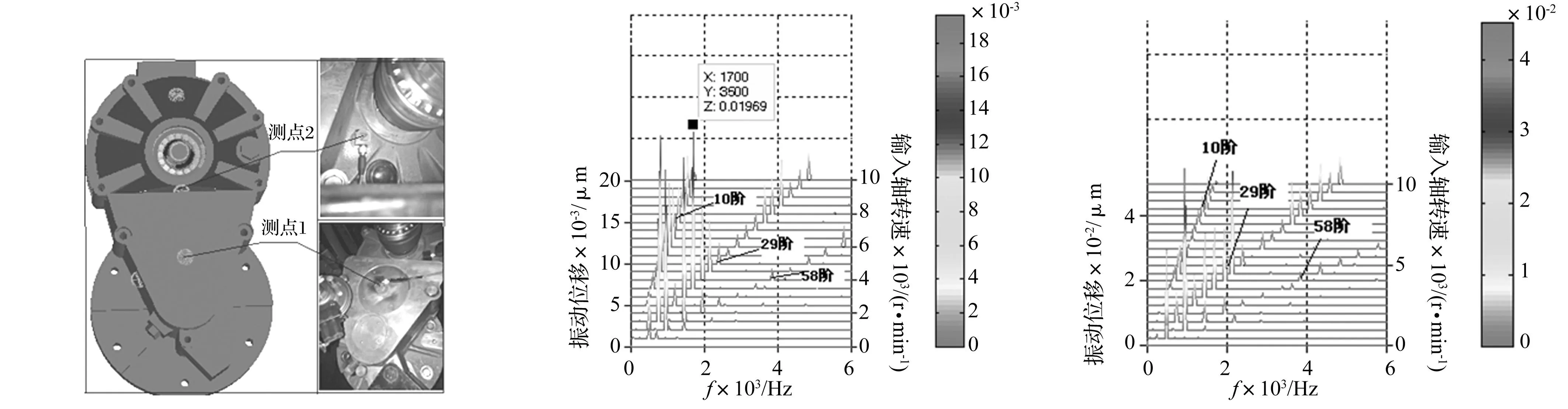
图9 仿真及试验测点分布Fig.9Measurementpointsinsimulationandtest图10 测点1振动阶次瀑布图Fig.10Vibrationwaterfallchartofpoint1图11 测点2振动阶次瀑布图Fig.11Vibrationwaterfallchartofpoint2

由图10、11知，测点1、2处的振动主要体现在10阶和29阶两个阶次，幅值最显著的29阶次对应输入轴小齿轮的齿数，幅值较小的10阶次由中间轴齿数和两级速比的分配共同决定[10]。另外的20阶(很小为标出)、58阶均为10阶、29阶的二倍频，体现了综合耦合模型的有效性，若只考虑齿轮系统振动而不考虑必要部件的柔性，则在仿真中无法获得这两个阶次。测点1处动位移在1 700 Hz(转速3 500 r/min)处出现峰值，结合表1可知该频率与齿轮系耦合模型的第14阶固有频率接近，引起该频率振动的主要原因是齿轮系统第9阶次共振；测点2处的振动位移在950 Hz(转速2 000 r/min)处出现峰值，结合表1可知该频率与齿轮系耦合模型的第6阶固有频率961.2 Hz接近，引起该频率振动的主要原因为减速器壳体1阶共振；其余各峰值的产生原因也可以结合表1依次进行甄别。

5减/差速器壳体动态响应试验

在半消声室内，转鼓试验台上进行整车状态下的振动噪声试验。试验车辆为所研究的集中式驱动纯电动车，在举升机上贴好加速度传感器，将车辆固定在转鼓试验台上，然后对应仿真点布置三向加速度传感器。由驾驶员操作车辆，使用LMS数采系统和CANCASE软硬件记录各工况下的振动信号，用于后续处理分析。试验主要测量减速器箱体表面的振动加速度(测点如图9右所示)、电机转速、转矩以及车速等信号，试验现场如图12所示。

试验工况分为两类，瞬态加速工况(以0-80 km/h为例)和稳态匀速工况(以40 km/h为例)。

首先给出输入轴转速为2 800 r/min，对应试验车速为40 km/h时的测试结果，以轴承6附近测点2的法向振动加速度为例，如图13所示为将该点加速度时域响应进行FFT频域分析的结果，较为显著的频率值有1 433Hz、1 991 Hz、2 540 Hz以及4 041 Hz，与图8仿真得到的轴承6频响曲线中的各个峰值吻合的较好，趋势也具有较好的一致性。尤其是4 000 Hz左右的双峰值体现了多柔性耦合模型预测的准确性。应该指出的是，接触式的方法很难直接测量轴承的振动情况，用接近轴承6的壳体表面测点2的振动情况对比仿真中轴承6的振动情况满足工程实际。

图12 转鼓振动试验Fig.12Vibrationtestondynamometer图13 测点2频域响应Fig.13Frequencyresonanceofpoint2图14 测点1加速度阶次图Fig.14Accelerationorderofpoint1

为进一步验证仿真结果，进行0~80 km/h瞬态加速工况下的加速度时域响应试验，并对测点的信号进行阶次分析。以测点1的数据处理结果为例，图14所示为该测点的加速度阶次分析结果。

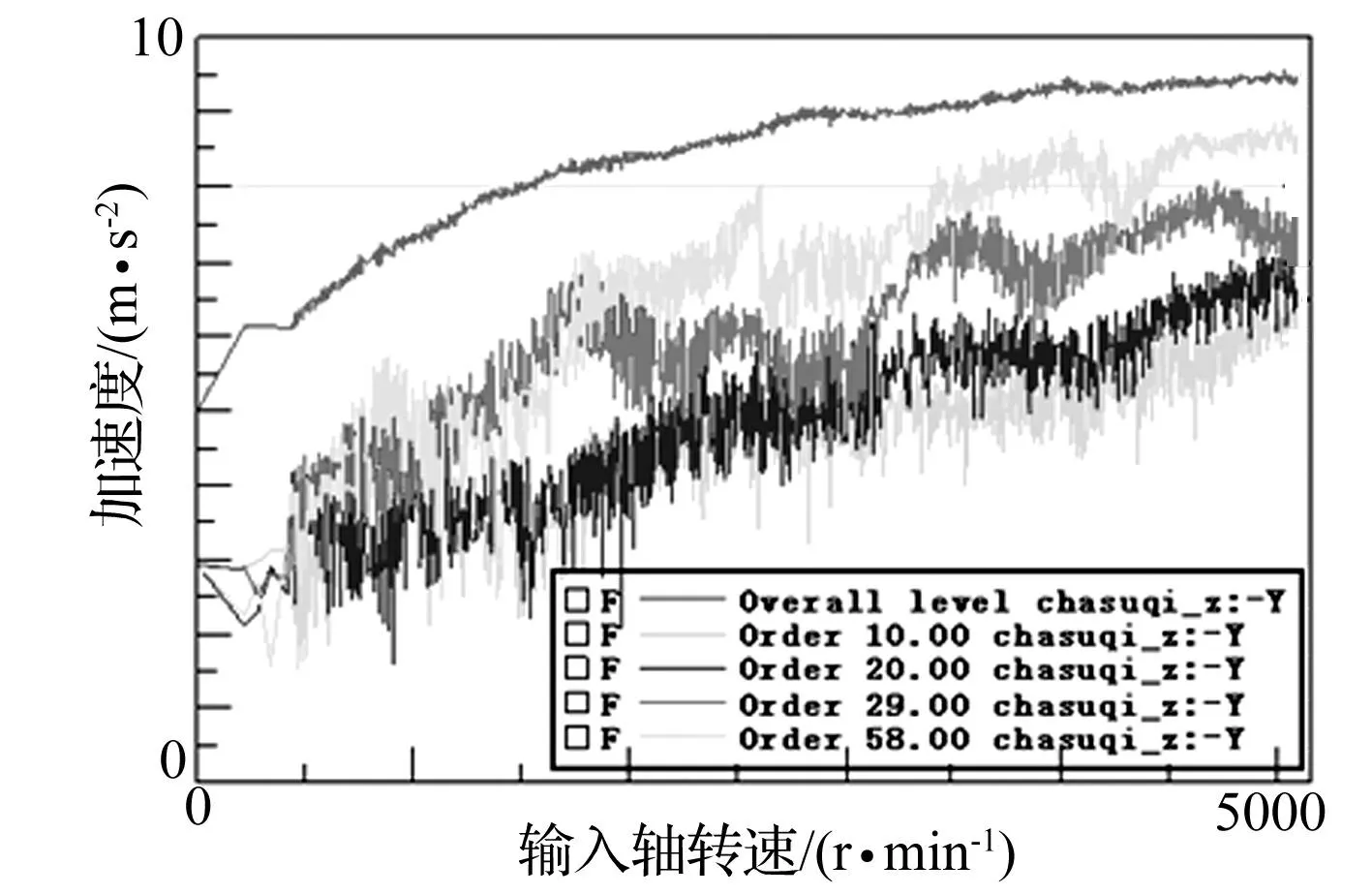
图15　测点1加速度前四阶切片 Fig.15 1 st-4 th slices of point 1

从图14中可以看出10、20、29、58四个阶次的振动幅值较大，与图10中仿真得到的测点1振动阶次图一致，说明仿真模型可以准确地反映和预测减/差速器的振动阶次特性。图14较好反映了振动的主要阶次，进一步对测点1振动阶次进行切片分析，可得到每个阶次下振动加速度幅值随转速的变化情况，如图15所示。图15中第10阶、29阶的振动幅值走势与图10中的仿真结果吻合的虽然不是特别理想，但1 000 Hz、2 000 Hz和4 000 Hz处的特征峰值都得到了很好的体现，仿真模型可用于后续优化设计。

6基于轮齿修形的振动性能优化

6.1齿轮噪声发生机理及控制方法

通过前述研究发现，电动车和传统车类似，其齿轮啮合噪声往往表现为一种哀鸣声(啸叫声)，其产生机理为啮合刚度激励和误差激励引起的齿轮轴的弯曲振动、扭转振动、轴向(横向)振动与摆动及系统的共振，而这又增大了动力啮合及轴承力，从而引起轴承与减/差速器壳体的相互作用，最后导致壳体及有关部件的振动和辐射噪声。所以要减小啸叫噪声的幅值，首先要减小振动的幅值。

啮合刚度及传递误差的幅值和特性取决于齿轮刚度及相互间的啮合情况，并直接影响动力总成的振动与噪声的幅值和特征。控制减/差速器内部齿轮啮合的好坏非常重要，通常有三类控制方法：①对齿轮及啮合进行最优设计，减少传递误差，包括优化齿形和提高制造精度；②尽可能增加齿轮的刚度，减小啮合时的齿轮变形；③对整个动力系统进行优化设计。选择第一类方法(优化齿形)进行振动性能的优化。

轮齿修形旨在减少由齿轮啮合过程中的啮合错位引起的偏载和齿侧间隙，减小齿轮在啮入和啮出过程中的冲击，改善齿面啮合，从而减小传递误差的幅值和波动，提高齿轮的动态振动性能，从源头上减小齿轮啸叫现象的产生。常用的轮齿修形方式主要有齿形修形和齿向修形两种。

6.2修形齿轮的选择

修形在Romax软件中进行，利用Romax自带的遗传算法，选择齿形(倾斜、鼓形)修形和齿向(倾斜、鼓形)修形相结合的修形方式，选取使传递误差波动幅值、齿面载荷、齿顶载荷比与齿根载荷比较小作为确定修形方案的评价指标，对相应的齿轮进行轮齿修形。结合第4.3小节“齿轮传递误差分析”的分析结果可知，与一级齿轮啮合相关的传递误差波动幅值，以及振动阶次响应相对于二级齿轮啮合要更为明显，因此选择一级齿轮副中的主动小齿轮作为修形齿轮进行优化，是较为经济和有效的选择。

6.3修形方法及修形量

针对一级齿轮副进行微观参数优化，选择优化方法为遗传算法，优化变量为齿形倾斜量、齿形鼓形量、齿向倾斜量和齿向鼓形量四个变量，在Romax的微观参数优化器中进行相关设置和优化求解。求解完成后，Romax给出推荐的修形方案，选择其中最优方案的修形量，如表2所示。一级小齿轮修形量的三维拓扑图，如图16所示。

表2　一级小齿轮修形方案

6.4优化仿真结果

评价修形效果的方式有很多，以一级齿轮传递误差波动幅值和减速器壳体上测点1处的振动位移阶次响应结果来评价修形效果。图17所示为修形前、后一级齿轮传递误差波动幅值的对比图。图18所示为修形后，减速器壳体测点1处的振动位移阶次图。

图16 一级小齿轮修形量三维拓扑Fig.163Dtopologyofpinion1modification图17 修形前、后传递误差波动幅值Fig.17Transmissionerrorbeforeandaftermodification图18 修形后测点1动位移Fig.18Vibrationwaterfallchartofpoint1aftermodification

从图17可以看出，一级齿轮副小齿轮经过轮齿修形后，一级齿轮传递误差波动幅值得以减小，与修形前(图6所示)的0.39 μm相比，修形后传递误差减小到0.23μm，减小幅度为40%；由图18可知，减速器壳体测点1处的振动位移得到了明显的衰减，与一级齿轮啮合相关的第10、29阶次动位移幅值明显减小，1 000 Hz、2 000 Hz及4 000 Hz等特征频率处的幅值也都得到明显的衰减。优化仿真结果表明，通过轮齿修形，可以有效地减小齿轮传递误差的波动，进一步使系统的振动响应的幅值得到减小，使齿轮系的阶次振动得到有效改善。进行轮齿微观修形是改善双级、单速比齿轮传动系统振动特性的有效途径。

7结论

(1)固有特性分析结果表明，减/差速器系统多柔性耦合模型，可以获得丰富的模态信息，将这些模态信息与单独考虑齿轮传动系的模态仿真结果、壳体模态试验结果比对，可以对振动源进行识别，并为后期的改进提供依据。

(2)从传递误差分析和轴承频响特性分析结果中发现，引发减/速器啸叫的结构因素可能有：一级齿轮传动系统的传递误差激励幅值较大、齿轮传动系和柔性壳体在高频段的模态耦合共振。

(3)壳体节点动态响应仿真得到的10阶次、29阶次振动由输入轴齿轮的齿数和两级减速比引发，该二阶次的幅值走势与对应测点的试验结果吻合较好，体现了多柔性仿真预测模型的准确性。

(4)通过轮齿微观修形，一级齿轮副传递误差波动幅值由0.39 μm减小到0.23 μm，使减/差速器壳体表面阶次振动幅值明显减小，其最大峰值由0.019 7 μm减小为0.008 5 μm。

啮合刚度及传递误差是引发齿轮系阶次振动及啸叫的主要激励，多柔性综合仿真预测模型可以较好的反映系统在激励作用下的响应情况，轮齿微观修形能有效减小齿轮副的传递误差，进而减小减/差速器表面的阶次振动，对啸叫问题的解决起到一定的积极作用。

参考文献

[1]陆波,朱才朝,宋朝省,等.大功率船用齿轮箱耦合非线性动态特性分析及噪声预估[J].振动与冲击,2009，28(4):76-80.

LU Bo, ZHU Cai-chao, SONG Chao-sheng, et al. Coupled nonlinear dynamic characteristics analysis and noise preestimation of a large burden marine gearbox[J]. Journal of Vibration and Shock, 2009,28 (4):76-80.

[2]周建星,刘更,马尚君.齿轮箱声固耦合系统噪声辐射研究[J].噪声与振动控制,2010:38-42.

ZHOU Jian-xing, LIU Geng, MA Shang-jun. Radiation noise analysis for structural-acousitc coupling system of gear-box [J]. Noise and Vibration Control, 2010:38-42.

[3]李瑰贤,马亮,陶建国,等.舰船用齿轮传动啮合刚度及动态性能研究[J].船舶工程,2000:41-43.

LI Gui-xian, MA Liang, TAO Jian-guo, et al. Mesh stiffness and dynamic properties of ship used gear[J]. Ship Engineering, 2000:41-43.

[4]魏静，孙清超，孙伟，等.大型风电齿轮箱系统耦合动态特性研究[J].振动与冲击,2012，31(8)：16-23.

WEI Jing, SUN Qing-chao, SUN Wei, et al. Dynamical coupling characteristics of a large wind turbine gearbox transmission system[J]. Vibration and Shock, 2012, 31 (8):16-23.

[5]刘辉，张喜清，项昌乐. 多源动态激励下变速箱箱体结构的动态响应分析 [J].兵工学报,2011，32(2)：129-135.

LIU Hui, ZHANG Xi-qing, XIANG Chang-le. Dynamic response analysis of gearbox housing under multi-source dynamic excitation[J]. Acta Armamentarii, 2011, 32 (2): 129-135.

[6]王立华，李润方，林腾蛟，等.齿轮系统时变刚度和间隙非线性振动特性研究[J].中国机械工程,2003,14(13): 1143-1146.

WANG Li-hua, LI Run-fang, LIN Teng-jiao, et al. Research on nonlinear vibration characteristics due to time-varying mesh stiffness and gear backlash in gear system[J]. China Mechanical Engineering, 2003,14 (13): 1143-1146.

[7]石珍，王家序，肖科，等.少齿差行星减速器振动特性仿真与实验研究[J].振动与冲击,2014,33(20):133-139.

SHI Zhen,WANG Jia-xu,XIAO Ke,et al.Vibration characteristics simulation and experimental research on a planetary reducer with small tooth number different[J].Journal of Vibration and Shock,2014,33(20):133-139.

[8]方源，于蓬，章桐.电动车动力总成模态试验与仿真分析[J].机械传动，2013,37(4)： 110-113.

FANG Yuan, YU Peng, ZHANG Tong. Test and simulation analysis of modal parameter of an Electric automotive powertrain[J]. Journal of Mechanical Transmission, 2013,37 (4):110-113.

[9]Yu P, Zhang T, Liu P H. NVH characteristic prediction of an electric vehicle reducer [J]. Advanced Materials Research, 2013, 608: 1656-1659.

[10]Chen F F, Yu P, Zhang T. Modal analysis for the powertrain of electric vehicle by finite flement method[J]. Applied Mechanics and Materials, 2013, 437: 140-145.

[11]陈锴.集中驱动式纯电动车减/差速器速比设计[D].上海：上海同济大学，2013.

[12]Welbourn D B. Fundamental knowledge of gear noise-a survey. Proe. Noise & Vib. Of Eng. and Trans., I Mech E., Cranfield, UK, July 1979:9-14.

[13]全源源.基于Romax的电动汽车变速箱的NVH分析[D].上海：上海同济大学，2012.