地震模拟振动台扩展系统理论分析及试验研究

第一作者李青宁男，硕士，教授，1952年4月生

通信作者程麦理男，博士生，1987年6月生

邮箱：cml3635@163.com

地震模拟振动台扩展系统理论分析及试验研究

李青宁，程麦理，尹俊红，闫磊，韩春，周春娟

(西安建筑科技大学土木工程学院，西安710055)

摘要：为利用单振动台进行空间大跨度结构动力试验，提出地震模拟振动台扩展系统概念。根据达朗贝尔原理对系统子台进行动力平衡分析，建立振动台扩展系统理论分析模型，通过考虑振动过程中上部结构对子台的动力影响，合理确定动力方程关键参数，改变系统参量可实现结构多点激励研究。设计并制作振动台扩展系统,试验结果表明，系统子台反应有明显时滞、增幅效应。试验及算例表明，该理论正确，方法可行，对地震模拟振动台试验系统的发展有实际意义。

关键词：振动台；扩展系统；子母台；理论分析；试验研究

收稿日期：2014-06-30修改稿收到日期：2014-10-23

中图分类号:TU311.3;TU317+.1

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.07.013

Abstract:In order to conduct the spatial large span structural dynamic tests by using a single vibration table，the concept of seismic simulation shaking table extended system was introduced. The dynamic balance analysis on the sub-station of the system was carried out according to the d’Alembert’s principle, and a theoretical analysis model of the shaking table extended system was established. The key parameters of dynamic equations were determined reasonably by considering the dynamic effect of upper structure on sub-station in the process of vibration analysis. The multi-point incentive study was achieved by varying system parameters. The shaking table extended system was designed and produced. The test results show that, the time lag effect and growth effect of the system sub-station response are significant. The test and numerical examples show that the theory is correct and the method is feasible. The results are of practical significance for the improvement of earthquake simulation shaking table test devices and the development of extended systems.

Theoretical and experimental analysis on shaking table extended system for seismic simulation

LIQing-ning,CHENGMai-li,YINJun-hong,YANLei,HANChun,ZHOUChun-juan(School of civil engineering，Xi’an University Of Architecture And Technology，Xi’an 710055,China)

Key words:vibration table; extended system; sub-and-master station; theoretical analysis; experimental study

人类在认识地震活动过程中，付出了惨重代价。为研究结构在地震动作用下，各构件的工作机理和破坏灾变过程，振动台试验显得必不可少。1970年美国加利福尼亚大学伯克利分校建成世界第一台地震模拟振动台[1]，使结构抗震研究进入新纪元。此后我国也在1983年8月自行研制3 m×3 m的振动台，填补我国地震模拟振动台的空白[2]。世界经济的飞速发展，大跨度空间结构建设日益频繁，为保证该类结构有良好的抗震性能，研究地震波空间差异对大跨度结构动力性能的影响，日本在1979年建成4个3 m×2 m水平单向振动台台阵系统[3]，开启世界利用台阵系统研究结构动力性能的历史。但由于台阵系统造价昂贵，试验、维护费用高，所以在国内外台阵系统数量仍然较少。对于平面展布尺寸较大的试验模型，可以尝试通过对单振动台进行改造设计，实现大跨度结构模型的振动台试验。

本文提出振动台扩展系统概念，对其进行合理扩展，实现单振动台的大跨度结构振动台试验研究。振动台扩展系统包括母台(原单振动台)、连接部件、子台(子振动台)，母台接收地震波信号，通过连接部件传递给子台，子台由于受到外载激励，将带动子台及上部结构发生振动。根据达朗贝尔原理，对子台进行动力平衡分析，建立振动台扩展系统动力平衡方程。为考虑大跨连体结构在振动过程中上部结构对子台的动力影响，引入拟静力模态矩阵概念，合理确定子台的等效质量。推导求解了振动台扩展系统在谐振荷载作用下的动力方程，根据解的形式分析了时滞、增幅效应的控制参数。试验和算例表明，本文理论正确，推导严密，方法可靠。

1振动台扩展系统理论

图1　振动台扩展系统 Fig.1 Shaker table extended system

通过分析地震模拟振动台扩展系统各构件工作机理，系统简化模型如下。

在进行扩展系统试验分析时假定：扩展系统的刚度、阻尼仅由连接部件提供，上部支座对子台刚度的影响较小，可忽略不计。实际振动台扩展系统工作过程中，子母台间地震波激励荷载的差异多表现在幅值、时差等方面，因而连接部件的刚度通常较大，即扩展系统刚度以连接部件刚度为主，忽略其它部分对扩展系统刚度的贡献。

图2　子台动平衡 Fig.2 Dynamic balance of sub-station

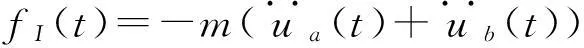
子台动力平衡方程有

(1)

式(1)即为地震模拟振动台扩展系统的振动方程。

分析式(1)可知，扩展系统子台动力平衡方程中未包含关于母台质量、刚度和阻尼等参量，因而子台动力响应与母台各动力参量无关；在实际振动台试验过程中，由于子台系统受结构模型振动的影响，使得在该子台的动力反应更加复杂。根据等效作用机理，分析认为：模型结构对子台的动力作用主要表现为结构惯性力对子台动力的作用，据此可考虑试验结构模型对子台动力响应的影响。取子台的等效质量为mB，根据下述三种情况确定子台等效质量。

(1)振动台系统空载工作时

根据地震模拟振动台扩展系统的动力运动分析可知，子台的等效质量为

mB=mb

(2)

(2)子台上设置独立结构模型

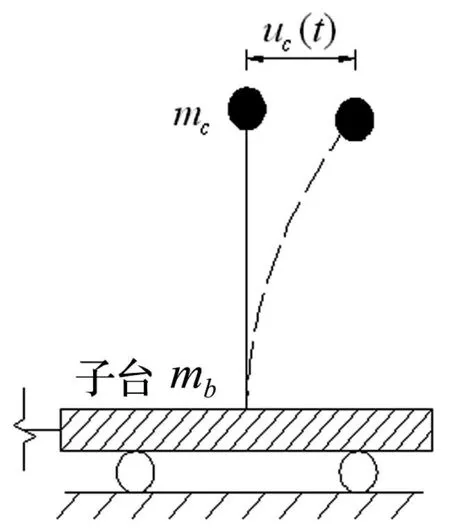
图3　子台设置独立结构模型 Fig.3 Setting independent structural model

当子台上放置独立结构模型时，模型底部与子台固结，分析简图如图3所示。

上部结构惯性力通过模型底部固结点完全传递给子台，则其等效质量为

mB=mb+mc

(3)

(3)子母台上设置连体结构

当子台与母台上放置有连体结构时，将上部结构考虑为质量集中模型，地震动模拟振动台分析模型可简化为图4所示。

由于子母台在振动工作过程有非一致激励效应，根据多点激励理论，地震模拟振动台扩展系统上设置连体结构的振动方程为

(4)

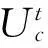
(5)

将式(5)代入式(4)的第一项，忽略所有动力项，结构动力运动方程式(4)退化为静力平衡方程

(6)

则非支座节点的拟静力位移可表示为

(7)

展开式(4)第二项，并忽略所有动力项

(8)

将式(7)变换后代入式(8)可知

(9)

Fb=λFc

(10)

(11)

式中：n为上部结构集中质量点数。

2振动台扩展系统求解

通过对地震模拟振动台振动方程式(1)分析可知，式中ub(t)为子台的动力输出位移。对于粘滞阻尼体系，一般动力荷载可通过傅里叶变换将其展开为多个谐振荷载分量，只要计算各谐振荷载作用下的反应并求和，即可得到结构的总反应[6]。因而对系统在谐振荷载作用下的动力响应求解很有实际意义。

ub(t)=(AcosωDt+BsinωDt)exp(-ξωt)+

(12)

式(12)中第一项为按照exp(-ξωt)衰减的瞬态反应，根据体系初始运动状态求解上式中的A、B。第二项为无限持续的稳态谐振反应。在地震模拟振动台扩展系统中，由于第一项的瞬态反应衰减较快，因而在分析研究中较常关注第二项的稳态谐振反应

(13)

则式(13)可表达为

(14)

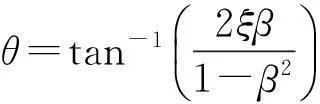
用动力扩大系数D表征子台动力响应的放大程度

(15)

该式表示子台动力输出相对母台的动力放大程度。结合大跨度结构抗震分析时，需考虑地震动的局部场地效应[9-10]，利用该动力放大系数实现大跨度结构局部场地影响研究。

3地震模拟振动台扩展系统设计

根据本文对振动台扩展系统的理论分析可知，在实际应用中，可根据实际试验模型的试验需求，对连接部件和子台各参量进行拟定，通过拟定的数值参量进行实际扩展系统的设计和制作。

依据某国家自然科学基金项目对某2 m×2 m地震动模拟振动台进行设计改造，制作振动台扩展系统，系统设计及实物如图5。

图5　扩展系统设计及制作 Fig.5 Extended system design and production

通过对地震模拟振动台扩展系统进行试验测试。限于篇幅，本文仅就扩展系统在Taft波120 gal、兰州波720 gal地震动荷载作用下，子母台动力反应时程如图6所示。通过分析可知，子母台的位移反应在各主要峰值处有明显增幅效应，地震波位移时程有显著时滞效应，即验证了该振动台扩展系统对母台主要动力参量的改变和调整，达到振动台扩展系统的目的。

图6 子母台动力反应对比Fig.6Comparethedynamicresponse图7 子母台动力响应时程Fig.7Dynamicresponsetimehistory

4算例

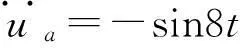
分析图7可知，振动台扩展系统子台动力反应相对母台有明显时滞、增幅效应。瞬态反应在2 ~ 3周后衰减消失，总反应趋于稳态反应。此外，系统子台动力反应稳定，易于控制。因而地震模拟振动台扩展系统方法可行，可应用于结构试验实践。

5结论

本文根据结构动力学原理，建立了地震模拟振动台扩展系统的计算模型。得到如下结论：

(1)根据结构多点激励公式的拟静力分析，提出拟静力模态矩阵概念，合理考虑大跨连体结构在振动时上部结构惯性力对子台的动力反应的影响。

(2)合理有效利用扩展系统子母台间动力输出差异，对地震波的空间变化进行研究模拟，可实现空间大跨结构的多点激励试验研究。

(3)通过试验模型分析和算例求解，验证本文理论正确、方法可行，可利用单振动台完成平面大跨度结构模型的振动台试验研究。

参考文献

[1]周颖,吕西林.建筑结构振动台模型试验方法与技术[M].北京:科学出版社,2012.

[2]黄浩华.3×3 m模拟地震振动台[J].地震学报,1986,8(1):72-78.

HUANG Hao-hua. 3 m×3 m earthquake simulation shaking table [J]. Journal of Earthquake,1986,8(1):72-78.

[3]纪金豹，李晓亮，闫维明，等.九子台模拟地震振动台台阵系统及应用[J].结构工程师,2011,27:31-36.

JI Jin-bao, LI Xiao-liang, YAN Wei-ming,et al. Research on the shaking table array and dynamic model test [J]. Structural Engineers,2011,27:31-36.

[4]屈铁军,王前信.多点输入地震反应分析研究的进展[J].世界地震工程,1993(1):30-36.

QU Tie-jun, WANG Qian-xin. Progress in the research of multi input seismic response analysis [J] World Earthquake Engineering,1993(1):30-36.

[5]李忠献,史志利.行波激励下大跨度连续刚构桥的地震反应分析[J].地震工程与工程振动,2003,23(2):68-76.

LI Zhong-xian,SHI Zhi-li. Seismic response analysis for long-span continuous rigid-framedbridges under excitation of traveling waves [J]. Earthquake Engineering and Engineering Vibration,2003,23(2):68-76.

[6]R.克拉夫,J.彭津,王光远等译校.结构动力学[M].北京:高等教育出版社,2011.

[7]闫晓宇,李忠献,韩强,等.多点激励下大跨度连续刚构桥地震响应振动台阵试验研究[J].土木工程学报,2013,46(7):81-89.

YAN Xiao-yu,LI Zhong-xian,HAN Qiang,et al. Shaking tables test study on seismic responses of a long-span rigid-framed bridge under multi-support excitations[J].China Civil Engineering Journal,2013,46(7):81-89.

[8]亓兴军,李小军,申永刚.地震行波输入下大跨连续刚构桥梁半主动控制效应分析[J].振动与冲击,2007,26(2):117-120.

QI Xing-jun, LI Xiao-jun, SHEN Yong-gang. Semiactive control effect analysis for long-span continuous rigid-framed bridge under seismic travelling wave input [J]. Journal of Vibration and Shock,2007,26(2):117-120.

[9]刘晶波.局部不规则地形对地震地面运动的影响[J].地震学报,1996,18(2):239-245.

LIU Jing-bo. Local effects of irregular topography on earthquake ground motion[J]. Journal of Earthquake, 1996,18(2):239-245.

[10]陈彦江,张德义,李晰.空间变化地震作用下钢管混凝土拱桥的抗震分析[J].工程力学,2013,30(12):99-106.

CHEN Yan-jiang, ZHANG De-yi, LI Xi, et al. Stochastic seismic analysis of a cfst arch bridge under spatially varying ground motions [J]. Engineering Mechanics, 2013,30(12):99-106.