协方差驱动随机子空间的Toeplitz矩阵行数选择方法

第一作者王燕女，硕士生，1990年生

通信作者韩晓林男，教授，1958年生

邮箱：xlhan@seu.edu.cn

协方差驱动随机子空间的Toeplitz矩阵行数选择方法

王燕1,2，杭晓晨1,2，姜东1,2，韩晓林1,2，费庆国1,2

(1.江苏省工程力学分析重点实验室,南京210096;2.东南大学土木工程学院,南京 210096)

摘要：随机子空间识别算法是一种基于环境激励的模态参数识别方法，仅需要响应时程便可识别模态参数。其中，协方差驱动随机子空间方法中Toeplitz矩阵行数的选取直接影响识别精度。通过构造相关矩阵，研究了Toeplitz矩阵行数i对协方差驱动随机子空间方法中奇异值分解去噪能力的影响。引入Toeplitz矩阵条件数，根据i与Toeplitz矩阵条件数的关系再次证明了i对识别精度的影响。研究了Toeplitz矩阵行数i的选择方法。采用两自由度弹簧振子系统和切尖三角翼模型两个仿真算例研究了Toeplitz矩阵行数i的选择方法。结果表明：在确定合适的系统阶数的前提下，Toeplitz矩阵的条件数越小识别精度越高。

关键词：随机子空间方法；阻尼识别；Toeplitz矩阵；条件数

收稿日期：2014-01-28修改稿收到日期：2014-04-03

中图分类号:TU317

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.07.011

Abstract:Stochastic Subspace Identification is a parameter identification method, which can effectively obtain modal parameters from the structural signal under ambient excitation. The choice of Toeplitz matrix row number directly influences the accuracy of identification. By constructing a correlation matrix, the influence of the dimension of Toeplitz matrix i on the denoising ability via SVD was derived. The concept of condition number was introduced in solving the system matrix. According to the relationship between i and condition number of Toeplitz matrix, it is proved once again that i has influence on identification accuracy. Then the selection method of Toeplitz matrix row number i was studied. Two examplic simulations in regard to a two-degree spring mass vibration system and a cropped delta wing model were presented to show the method in the selection of i. The results show that on the premise of determining a suitable system order, the smaller the Toeplitz matrix condition number is, the higher the identification accuracy is.

Selection method of Toeplitz matrix row number based on covariance driven stochastic subspace identification

WANGYan1, 2,HANGXiao-chen1, 2,JIANGDong1, 2,HANXiao-lin1, 2,FEIQing-guo1, 2(1. Jiangsu Key Laboratory of Engineering Mechanics, Nanjing 210096,China;2. Department of Engineering Mechanics, Southeast University, Nanjing 210096, China)

Key words:stochastic subspace identification; damping identification; Toeplitz matrix; condition number

随机子空间方法可以在激励未知、仅有响应数据的情况下识别系统的模态参数。根据识别过程中具体算法的不同，随机子空间可以分为数据驱动随机子空间和协方差驱动随机子空间[1-2]。协方差驱动随机子空间通过分解结构振动响应输出数据协方差矩阵(Toeplitz矩阵)的奇异值得到系统矩阵，进而识别系统的模态参数[3]。

协方差驱动随机子空间方法中Toeplitz矩阵行数i与数据驱动随机子空间方法中的Hankel矩阵行数i概念相同，都是人为选择的参数。一般认为，i的选取只会对计算速度产生影响。Overschee[4-6]最先提出了数据驱动随机子空间方法，并对Hankel矩阵行数的取值范围做了简要介绍，他提出Hankel矩阵的行数需大于系统阶数。陈爱林等[7]通过统计分析得到了识别精度最佳时Hankel矩阵行数与系统阶数的关系，总结出实际应用中随机子空间方法关于i的选取方法。刘东霞[8]研究了协方差驱动随机子空间算法在桥梁中的模态参数识别，分析了Hankel矩阵行和列的关系。辛峻峰等[9]推导了Hankel矩阵维数与数据驱动随机子空间方法去噪能力的理论关系，研究了数据驱动随机子空间方法Hankel矩阵维数对识别精度带来的影响。

本文推导了Toeplitz矩阵行数i与协方差驱动随机子空间方法奇异值分解的理论关系，并且从条件数着手，分析了i对求解系统矩阵的影响。证明了Toeplitz矩阵行数i不仅对计算速度产生影响，对协方差驱动随机子空间方法的识别精度也有着不可忽视的影响，继而提出了协方差驱动随机子空间方法的Toeplitz矩阵行数i选择方法。

1协方差驱动随机子空间的理论基础

在协方差驱动随机子空间方法中，首先将响应数据表达为Hankel矩阵，然后计算协方差序列组成Toeplitz矩阵，主要作用在保持信号原有信息的情况下缩减数据量，从而减少计算时间。再通过矩阵的奇异值分解和特征值分解求出系统矩阵，进而识别结构的模态参数。

Hankel矩阵定义为：

Hankel矩阵Y0/2i-1是包括“2i行块”、j列块的矩阵。每一块行由l行组成，l是输出通道数。理论上假设j→∞，但实际上j不可能是无穷大的。Hankel矩阵分块为“过去”和“将来”两部分，下标0/2i-1表示Hankel矩阵的第一列的第一块行和最后一块行的下标，下标p和f分别表示“过去”和“将来”。矩阵分成Yp和Yf将Y0/2i-1分成相等的两部分，每一部分都有i块行。

(2)

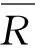
(3)

计算所得协方差序列组成Toeplitz矩阵，表示如下：

(4)

由状态空间方程的定义可以推导：

T=ΓΘ

(5)

如果系统是可观和可控的，则Toeplitz矩阵的秩为系统阶次n。对Toeplitz矩阵进行奇异值分解，秩反映在不为零的奇异值数量上：

T=USVT=

(6)

式中，U，V都是正交矩阵，S是由正奇异矩阵组成的对角阵，U1∈Rli×n,S1∈Rn×n,V1∈Rli×n，奇异值按降序排列：

σ1≥σ2≥…≥σn≥0

(7)

比较式(4)和式(5)，可观矩阵和可控矩阵可以表示如下：

(8)

式中，F为n阶非奇异矩阵，为简单起见，可取F为单位矩阵I，上式可以变为：

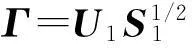
(9)

同样定义T2如下：

T2=ΓAΘ

(10)

T2和T具有相同的结构，T2包含的协方差从2到i+1。根据式(9)和式(10)可以解得A:

(11)

根据Γ和Θ的定义可知，C等于Γ的前l行，其中l为通道数。

对于离散系统，对状态矩阵进行特征值分解：

A=ΨΛΨ-1

(12)

最后，根据系统矩阵的特征值及特征向量识别出系统的模态参数频率和阻尼。

2矩阵行数与奇异值分解的关系

由式(3)和(4)可知Toeplitz矩阵由以下两部分组成：

(13)

式中S表示真实信号，C表示噪声。

根据系统的阶次n设定阀值，n的确定可以参见文献[10-12]。对所计算的Toeplitz矩阵进行奇异值分解得到：

(14)

式中，正交矩阵U∈Ri×i、U1∈Ri×n、U2∈Ri×(i-n)，且V∈Ri×i、V1∈Ri×n、V2∈Ri×(i-n)也为正交矩阵。S∈Ri×i、S1∈Rn×n、S2∈R(i-n)×(i-n)为对角矩阵。n≤i为系统的阶数。

构造矩阵：

(15)

由于信号与噪声不相关，所以上式可以写成：

(16)

由上式可知，HC为噪声C的协方差矩阵，设已知噪声的方差为η2，则噪声C的协方差矩阵为[13]

HC=η2Ii

(17)

式中，Ii为i阶单位阵。根据式(6)有

(18)

(19)

(20)

由式(17)和式(20)可以得到：

(21)

则结合式(18)~(21)知：

(22)

为了便于分析，将S2表示为如下形式：

(23)

即:

S1=(S2n-iη2In)1/2

(24)

式(24)表明，在数据总量不变时，S1取决于Sn，Toeplitz矩阵行数i和系统的阶数。而Sn取决于系统的阶数n。所以，在数据总量固定时Toeplitz矩阵行数i和噪声方差η都会影响SVD的去噪能力，从而影响算法的识别精度。

3矩阵行数对Toeplitz矩阵条件数的影响

由式(10)对T2的定义可知：

T2=TA

(25)

为求系统矩阵A则需求解式(25)所示的线性方程组，根据系统矩阵A可以解得系统的模态参数。因此，系统矩阵A的精度决定了模态参数识别结果的识别精度。式(25)可能是病态的，此时T和T2的微小扰动将引起系统矩阵A较大的改变。由此可以根据Toeplitz矩阵即T矩阵的条件数来判断该线性方程组是否是病态方程组。

由式(4)可知，Toeplitz矩阵为i×i的方阵(通道数为l时)，i为人为选择的参数。当i取不同值时，Toeplitz矩阵的条件数也会发生变化，从而导致输出数据的扰动对系统矩阵的求解产生不同的影响。当Toeplitz矩阵条件数越小，响应数据的扰动对系统矩阵的扰动越小，从而导致根据系统矩阵求解的模态参数误差更小。所以，Toeplitz矩阵条件数越小，系统的识别精度越高。

4Toeplitz矩阵行数i的选择方法

设响应数据总长度为s，Hankel矩阵行数和列数满足关系：

s=2i+j-1

(26)

式中i表示Hankel矩阵有2i个行块，同时i与Toeplitz矩阵的行块或列块相等。j表示Hankel矩阵有j个列块。

理论上j→∞，根据经验值j>20i，所以i需满足

(27)

另一方面，Toeplitz矩阵的行数i需满足[4]：

i>n

(28)

式中n为系统的阶数。

综上所述，提出一种通用的Toeplitz矩阵行数i取值方法：在满足(27)和(28)的前提条件下，确定合适的系统阶数，计算不同i值对应的Toeplitz矩阵的条件数，选取条件数较小时对应的i值，进行识别计算。

5仿真算例

5.1两自由度弹簧振子系统

图1　弹簧振子系统 Fig.1 Spring mass system

如图1所示，k1=10 000N/m，m1=0.5 kg，k2=5 000 N/m，m2=0.2 kg。设模态阻尼比为3%，该系统的第一阶和第二阶频率分别为17.062 Hz和33.135 Hz。在质量块m2施加白噪声激励，响应数据采样频率为160 Hz (截止频率为50 Hz)，采样时间为100 s，数据总长为16 000。

图2为该系统的稳定图，根据稳定图确定系统阶数为4。由于频率的识别结果精度比较高，这里不做比较。表1为Toeplitz矩阵行数i按公差为2的等差数列选取的阻尼识别结果以及相应的Toeplitz矩阵谱条件数。

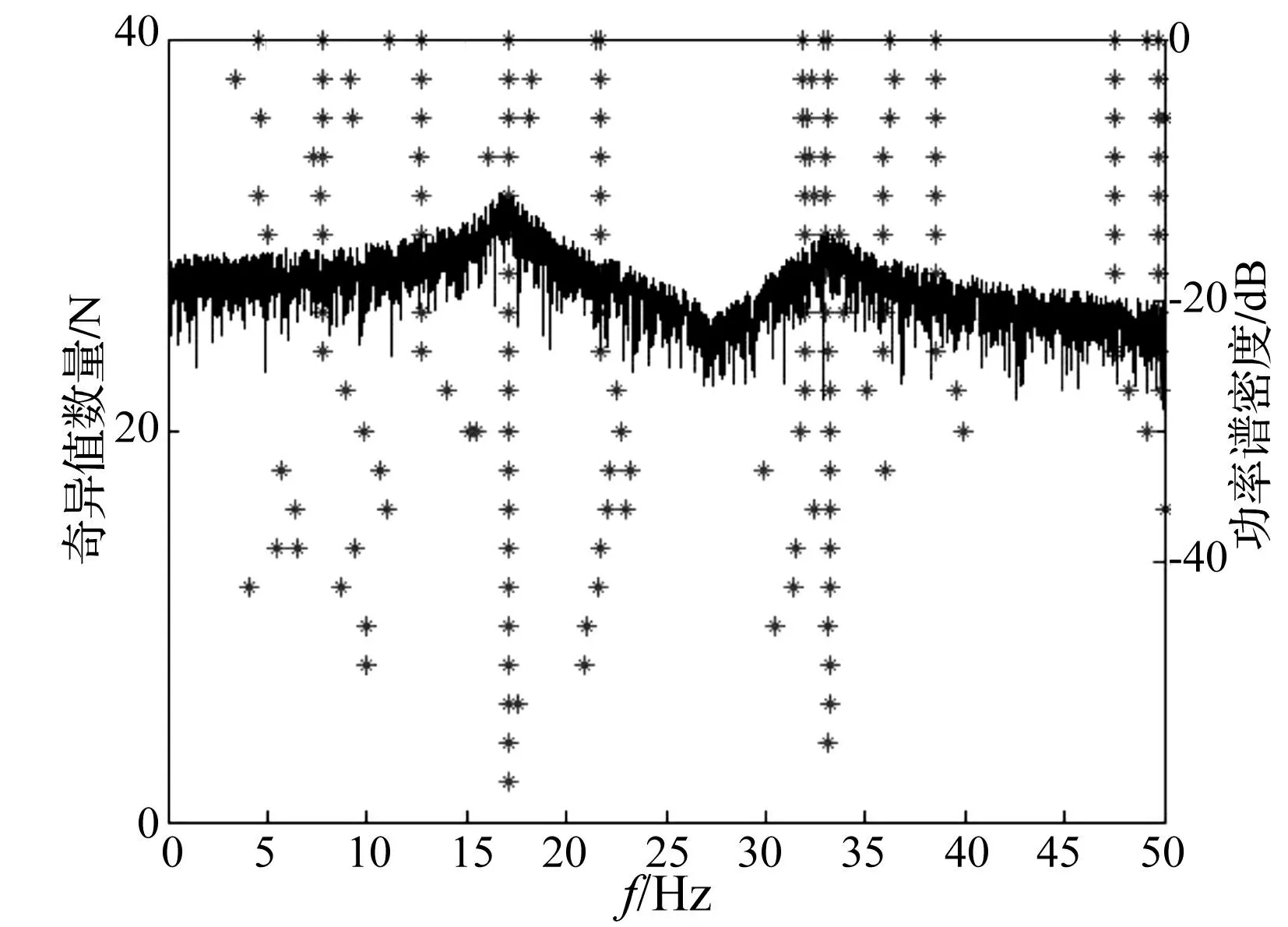
图2　弹簧振子系统的稳定图 Fig.2 Stabilization diagram of spring mass system

观察表1可以发现：

(1)协方差驱动随机子空间算法能比较精确的识别出该弹簧振子系统的阻尼参数；

(2)当i=12时，第一阶模态的识别误差最小，达到-0.19%。当i=6时，第二阶模态的识别误差最小。

(3)当i=10时，Toeplitz矩阵的谱条件数最小，为7.22e15，此时两阶识别结果的平均绝对误差最小，为1.07%，说明在条件数最小时获得最优的识别结果。

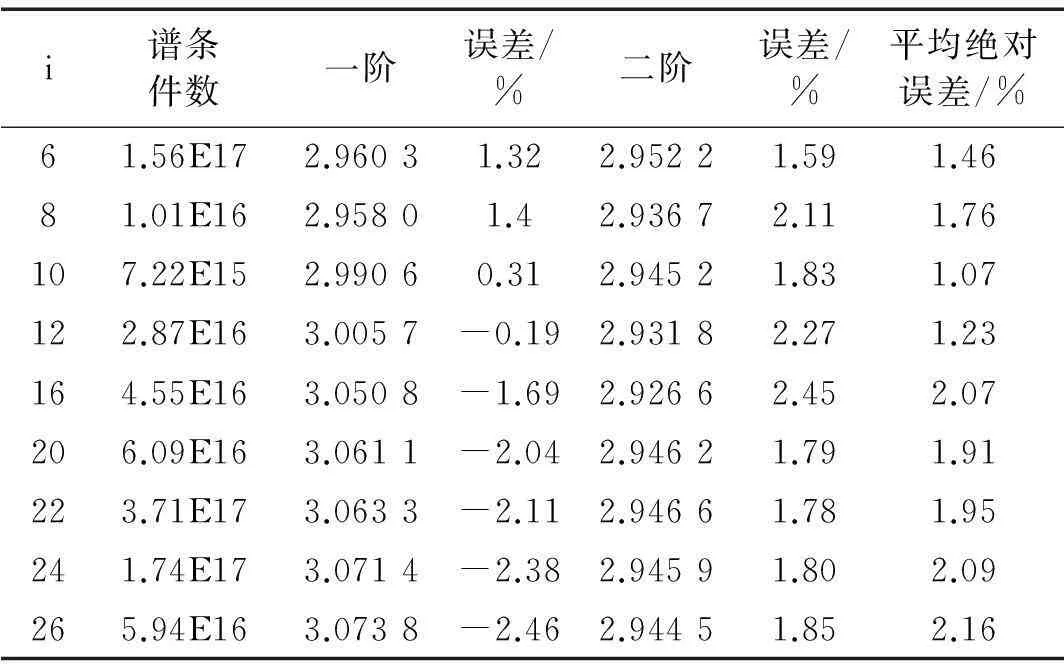
表1　弹簧振子系统的阻尼识别结果

5.2切尖三角翼的阻尼识别

图三为切尖三角翼的几何尺寸，翼板厚度为0.016 m。弹性模量为71.161 2 GPa，剪切模量为27.100 4 GPa，泊松比为0.324 8。选取翼板翼根为固定端，建立有限元模型。在翼板的上表面施加白噪声面压。响应数据采样频率为1 800 Hz，采样时间为10 s，数据总长度为18 000。设阻尼为3%的模态阻尼，对应各阶频率均为3%，提取如图4所示的六个点的位移响应。

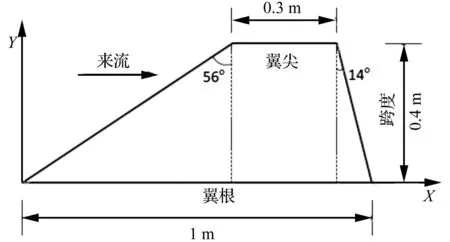
图3　切尖三角翼的几何尺寸 Fig.3 The geometric size of the cropped delta wing

图4　切尖三角翼的有限元模型 Fig.4 The finite element model of the cropped delta wing

同样地，由于频率的识别结果精度比较高，这里只比较阻尼的识别结果。采用仿真一的方案选取i进行识别计算。根据如图四所示的稳定图，确定系统的阶数为10阶。阻尼识别结果和相应的谱条件数如表2所示。

由表2可以观察到：

(1)协方差驱动随机子空间算法能够比较精确地识别出系统的前四阶模态参数。但当i取值较大时，识别结果出现遗漏模态。

(2)当i=12~28时，各阶模态的阻尼识别的最小误差不尽相同。当i=12时，Toeplitz矩阵的谱条件数最小，为1.73e17，此时前四阶模态阻尼的平均绝对误差最小，为1.23%。可以得到与两自由度算例相同的结论，即：条件数最小时获得最优的识别结果。

表2　切尖三角翼的阻尼识别结果及Toeplitz矩阵的谱条件数

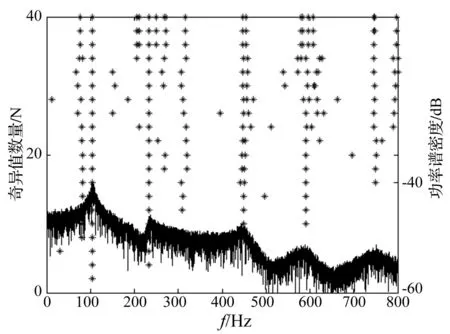
图5　切尖三角翼模型的稳定图 Fig.5 Stabilization diagram of the cropped delta wing

6结论

本文利用奇异值分解的理论推导和线性方程组中条件数这一数学工具，分析了协方差驱动随机子空间中Toeplitz矩阵行数i的选择对识别精度的影响。提出了一种协方差驱动随机子空间算法Toeplitz矩阵行数i的选择方法：在确定合适的系统阶数后，选取不同的i值，分别计算不同i值对应的Toeplitz矩阵的条件数，选取条件数较小时对应的i值，进行识别计算。通过两个算例仿真表明：i越大，求解系统矩阵A的线性方程组病态越严重；Toeplitz矩阵行数i对识别精度的影响至关重要，不同系统为达到最好识别精度，i的取值不是固定的；当条件数较小时，识别精度比较理想，由此证明了本文提出的Toeplitz矩阵行数i选择方法的可行性。根据本文的结论，更加方便地得到i的选取方法，并且该方法确定的i能更加精确的识别出系统的模态参数。

参考文献

[1]辛峻峰, 王树青, 刘福顺. 数据驱动与协方差驱动随机子空间法差异化分析[J]. 振动与冲击, 2013,32(9):1-5.

XIN Jun-feng, WANG Shu-qing, LIU Fu-shun. Performance comparison for data-driven and covariance-driven stochastic subspace identification method[J]. Journal of Vibration and Shock, 2013,32(9):1-5.

[2]Boonyapinyo V, Janesupasaeree T. Data-driven stochastic subspace identification of flutter derivatives of bridge decks[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010, 98(12): 784-799.

[3]李永军, 马立元, 王天辉, 等. 协方差驱动子空间模态参数辨识方法改进分析[J]. 中国机械工程, 2012, 23(13): 1533-1536.

LI Yong-jun, MA Li-yuan, WANG Tian-hui, et al. An improvement on subspace modal parameter identification algorithm driven by covariance[J]. China Mechanical Engineering, 2012, 23(13):1533-1536.

[4]Van Overschee P, De Moor B. Subspace identification for linear systems: theory, implementation, applications. dordrecht, Netherlands: Kluwer Academic Publishers, 1996.

[5]Van Overschee P, De Moor B. Subspace algorithms for the stochastic identification problem[J]. Proceedings of the 30thIEEE Conference on Decision and Control, pages 1321-1326,Brighton,UK,1991.

[6]Van Overschee P, De Moor B. Subspace algorithms for the stochastic identification problem[J]. Automatica, 1993, 29(3): 649-660.

[7]陈爱林,张令弥.基于随机子空间方法的模态参数识别研究[J].中国航空学报，2001(4):222-228.

CHEN Ai-lin, ZHANG Ling-mi. Study of stochastic subspace system identification method[J].Chinese Journal of Aeronautics,2001(4):222-228.

[8]刘东霞. 基于随机子空间法的梁桥模态参数识别 [D]. 成都: 西南交通大学, 2008.

[9]辛峻峰, 盛进路, 张永波. 数据驱动随机子空间法矩阵维数选择与噪声问题研究[J]. 振动与冲击, 2013, 32(16): 152-157.

XIN Jun-feng, SHENG Jin-lu, ZHANG Yong-bo. Relation between noise and matrix dimension of data-driven stochastic subspace identification method[J]. Journal of Vibration and Shock, 2013, 32(16):152-157.

[10]樊江玲. 基于输出响应的模态参数辨识方法研究 [D]. 上海：上海交通大学, 2007.

[11]Hong A L, Ubertini F, Betti R. New stochastic subspace approach for system identification and its application to long-span bridges[J]. Journal of Engineering Mechanics, 2012, 139(6): 724-736.

[12]Loh C H, Liu Y C, Ni Y Q. SSA-based stochastic subspace identification of structures from output-only vibration measurements[J]. Smart Structures and Systems, 2012, 10(4-5): 331-351.

[13]张波, 李健君. 基于 Hankel 矩阵与奇异值分解 (SVD) 的滤波方法以及在飞机颤振试验数据预处理中的应用[J]. 振动与冲击, 2009, 28(2): 162-166.

ZHANG Bo, LI Jian-jun. Denoising method based on Hankel matrix and SVD and its application in flight flutter testing data preprocessing[J]. Journal of Vibration and Shock, 2009, 28(2):162-166.

[14]易大义, 陈道琦. 数值分析引论[M]. 杭州：浙江大学出版社, 1998, 9.