一种多轴向随机激励下结构疲劳寿命分析方法

第一作者贺光宗男，博士生，讲师，1980年生

一种多轴向随机激励下结构疲劳寿命分析方法

贺光宗1,2，陈怀海1，贺旭东1

(1.南京航空航天大学航空宇航学院，南京210016； 2. 山东理工大学交通与车辆工程学院，山东淄博255049)

摘要：提出了一种多轴向随机激励下结构疲劳寿命估计的频域分析方法。首先，对结构进行频响分析，得到在基础加速度激励下的应力频响函数矩阵，通过随机振动分析，得到结构应力的功率谱密度矩阵；其次，采用等效的Von Mises应力功率谱密度将多轴应力问题转化为单轴应力问题；最后，利用单轴应力疲劳寿命估计的频域分析方法对结构疲劳寿命进行估计。对一典型构件在多轴向随机激励下的疲劳寿命进行了计算,并与实验结果进行了对比。另外，对构件在多轴向同时激励与单轴分别激励的疲劳损伤结果进行了对比分析，表明多轴向同时振动具有明显的多轴效应，因此进行多轴向振动疲劳研究十分必要。

关键词：多轴向随机激励；振动疲劳；寿命估计；多轴效应

基金项目：国家自然科学基金(11102083)

收稿日期：2014-01-27修改稿收到日期：2014-06-08

中图分类号:O346.2；TH114

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.07.009

Abstract:A frequency domain method for fatigue life prediction of structures under multi-axial random excitations was presented. The transfer function matrix from the excitation accelerations to the response stresses was obtained through frequency response analysis. According to the random vibration theory, the PSD matrix of stress response was calculated. Then, the multi-axial stress problem was translated to a uniaxial stress problem via equivalent PSD of Von Mises stress and the uniaxial frequency domain fatigue analysis was used for the fatigue life prediction. The fatigue life of a typical component under the multi-axial random excitations was calculated and compared with the test results. In addition, the fatigue damages of the component caused by the simultaneous multi-axial and uniaxial excitation were analyzed and compared and the multi-axial effect was also analyzed. The result shows the necessity of the application of multi-axial excitations in fatigue life prediction.

Vibration fatigue life prediction method for structures under multi-axial random excitations

HEGuang-zong1,2,CHENHuai-hai1,HEXu-dong1(1. Aerospace College, Nanjing University of Aeronautics and Astronautics,Nanjing 210016 China；2. School of Transportation and Vehicle Engineering, Shandong University of Technology, Zibo 255049,China)

Key words:multi-axial random excitation; vibration fatigue; fatigue life prediction; multi-axial effect

工程构件或产品在实际工作中所受的载荷一般是多轴向的，但是由于技术和试验条件的限制，目前对工程构件或产品进行的耐久性试验和应力筛选试验，大多数采用单轴向依次振动的等效试验方法[1]。对试验对象在三个正交方向上分别依次进行单轴向振动试验，以近似等效其所处的多轴向振动环境。两者之间的差异通过增加振动时间或提高振动量级的方法给予补偿。现行的标准GJB150.16A和MIL-STD-810F均采用此类方法。但是，单轴向振动试验中增加的时间和提高的量级一般通过工程经验确定，没有相关的标准。另外，单轴向试验振动方的向与结构疲劳失效的敏感方向可能不重合，导致产品通过了单轴等效耐久性试验，却在实际的振动环境中却发生了疲劳失效[2]。

对于多轴向振动技术及其与单轴振动的差别越来越引起人们的重视。夏益霖等[3-4]总结了多轴振动环境试验的发展现状,并对多轴振动环境试验的定义、基本原理、关键技术和解决途径进行了讨论。陈颖等[5]对典型试件进行了单、多轴随机振动试验。指出了单轴向振动和多轴向同时振动能引起结构的不同模态，产生不同的激发效果。对于单轴向依次振动与多轴向同时振动的疲劳问题，French等[6-7]对典型试件进行了试验研究。试件结果表明：多轴向同时振动与单轴向依次振动疲劳试验相比较具有明显的多轴效应。两种工况下试件的疲劳失效时间和失效位置均存在差异，多轴向同时振动更能导致结构疲劳失效。目前对多轴向振动引起的结构疲劳问题的研究主要集中在定性分析和试验方面，对多轴效应的量化和理论研究较少。本文对多轴向激励下的振动疲劳问题进行了理论分析，计算了不同激励工况下构件的疲劳损伤，并对构件在多轴向振动激励下的多轴效应进行了研究。

对于实际的工程构件，在多轴随机振动环境下其应力响应一般也是多轴的，各应力分量均为随机过程，而且是一般非比例的。目前对于多轴疲劳寿命估计的主要方法有等效应力应变法、能量法和临界损伤平面法[8]。临界平面法从疲劳失效机理出发建立了多轴疲劳失效模型，但是往往只适用于特定材料或载荷。等效应力应变方法将复杂的应力、应变转化为等效应力和等效应变,利用单轴疲劳分析理论对多轴疲劳寿命进行估计。该方法计算量小，适合工程应用。本文将等效应力方法应用于多轴向激励引起的多轴疲劳问题。利用有限元分析软件NASTRAN对结构进行频响分析，得到结构应力分量的频响函数矩阵，并通过随机振动分析得到结构的应力响应的功率谱密度矩阵；采用等效的Von Mises应力功率谱密度将多轴应力问题转化为单轴应力问题，进而利用单轴频域方法对结构寿命进行估计。通过对多轴向随机激励下的典型构件进行疲劳寿命估计,验证了方法的可行性。

1Von Mises应力等效应力寿命估计频域法

1.1多轴向激励载荷谱

为了模拟实际工况的振动环境，在随机振动试验中一般采用基础激励的方式对结构进行激励，激励载荷谱为加速的功率谱密度。对于多轴向随机振动试验，其载荷谱形式为：

(1)

式中，矩阵对角线上元素为各振动方向加速度的自功率谱密度，非对角线元素为各方向互功率谱密度，并且满足：

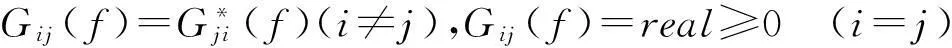
1.2动力学响应分析

由随机振动理论，结构的应力响应可以由激励和结构频响函数得到

(2)

当系统的输入为多轴向激励时，结构某点的应力响应的功率谱密度矩阵可以表示为：

(3)

式(3)中的频响函数矩阵为：

Hσ(f)=

(4)

式中，Hσy,x 表示结构在x向单位加速度激励下该点应力σy的频响函数。

将式(1)和式(4)代入式(3)即可的到应力的功率谱密度矩阵，Gσσ(f)为6×6×n矩阵，n为分析频率点数。其中对角线元素为各应力分量的自功率谱密度，为实数；非对角线元素为各应力分量间的互功率谱密度，为复数，且关于对角线对称的互功率谱密度间互为共轭复数。

1.3Von Mises等效应力功率谱密度的确定

Von Mises应力在三向应力状态下定义为：

(5)

应力向量为σ=(σx,σy,σz,τxy,τxz,τyz)T，则式(5)可以表示为：

(6)

式中，A为对称矩阵，且

对式(6)两边求数学期望可得应力均方值

(7)

式中，E[σσT]为应力向量的协方差矩阵，它与功率谱密度矩阵应力分量的关系为

(8)

等效Von Mises 应力过程的均方根值与其功率谱密度函数Gσeq(f)存在关系式

(9)

由式(6)~(9)可以定义等效Von Mises应力功率谱密度函数

Gσeq(f)=Trace[AGσσ(f)]

(10)

式中，等效Von Mises应力为高斯随机过程，可以由各应力分量的功率谱密度计算得到。

1.4频域内的疲劳寿命估计

通过式(10)得到了等效Von Mises应力功率谱密度，可以直接用于单轴疲劳寿命估计的频域分析。其基本过程为：

由式(11)计算等效Von Mises应力功率谱密度的各阶谱矩

(11)

根据Miner线性疲劳累积损伤理论，结构的疲劳

损伤为

(12)

式中，ni表示第i级应力水平下的应力循环次数；Ni表示应力水平为Si时的疲劳寿命。

对于连续应力状态，在时间T内应力值落区间(Si-dS/2,Si+dS/2)的次数为ni=E[P]Tp(Si)dS

采用S-N曲线三参数式N(S)=Sf(S-Sae)b,因此在应力为Si时的循环次数Ni=Sf(Si-Sae)b。

则连续分布的应力状态下时间T内的疲劳损伤为

(13)

按照Miner 线性累积损伤理论，当损伤值E[D]等于1时结构发生破坏，此时疲劳寿命为:

(14)

由式(14)可知频域疲劳寿命损伤估计关键是确定应力幅值概率密度函数p(S)，目前有很多计算模型，如Tunna、Wirsching、Hancok及Chaudhury模型[9]，通过实际工程应用证明：在处理窄带随机过程时采用Bendat模型，处理宽带随机过程是采用Dirlik模型能取得更高的计算精度。其表达式为：

Bendat模型：

(15)

Dirlik模型：

(16)

式中，参数m0,D1,D1,Q,Z,R均可由式(11)确定的零阶、二阶和四阶谱矩计算得到[10]。

2方法的应用

多轴向激励下结构的振动疲劳分析过程如图1所示。该方法的实现需要借助有限元分析软件NASTRAN和计算软件MATLAB。NASTRAN仅用于结构频响函数的获取，通过对结构进行单位加速度的基础激励，然后进行频响分析实现。通过工程实测和数据处理得到激励的功率谱密度矩阵Ga(f)，结合NASTRAN分析得到的频响函数矩阵Hσ(f)数据，通过MATLAB编制程序计算结构疲劳损伤和疲劳寿命。

图1　疲劳损伤计算流程图 Fig.1 Flow Diagram of damage calculation

3算例分析

以文献[7]中试验件为分析模型，进行多轴激励下的疲劳寿命分析。试件尺寸参数如图2(a)所示，材料为铝合金2024-T4。文献[7]中将其固定于三轴向振动台面上，进行了单轴向激励与多轴向同时激励下的振动疲劳实验研究。

图2　疲劳分析模型和计算点分布图 Fig.2 Model and analysis point of damage calculation

在NASTRAN中对模型进行了数值建模，采用大质量法分别在固定端施加单位加速度基础激励，得到结构在不同激振方向上各点上应力分量与单位加速度的频响函数。在危险面(缺口处半径最小截面)上选取具有代表性的三点(计算点位置如图2(b)所示)，进行了单轴或多轴同时激励下的振动疲劳分析计算。

三轴向同时振动和单轴向振动计算中的加速度载荷谱采用相同的谱形，如图3所示。文献[7]中载荷谱截止频率为85 Hz，结构一阶固有频率为86.1 Hz。在实际振动过程中随着结构损伤的出现，其固有频率会降低，使结构产生持续共振，加速结构的疲劳失效[9]。考虑到仿真与实际问题的区别，本文计算载荷谱截止频率提高到90 Hz，为保证振动输入能量不变，频带宽度和加速功率谱密度值均与文献[7]相同。

图3　激励加速度功率谱密度 Fig.3 The input accelerations PSD

计算了不同工况下等效Von Mises应力的功率谱密度，图4为计算点2在三轴同时振动时的Von Mises 等效应力的功率谱密度。

图4　等效Von Mises 应力功率谱密度 Fig.4 Theequivalent Von Mises stress PSD

分别计算了各点在三轴向同时激励和单轴向激励下的疲劳寿命，计算分析中不考虑各方向间载荷的相关性。由于Z向振动引起的应力响应很小，对结构疲劳损伤的影响可以忽略不计。计算结果如表1所示，计算分析中根据加速激励谱的谱形特点，应力幅值概率密度函数采用Bendant窄带模型进行疲劳寿命分析。材料的S-N曲线采用幂函数公式，在对数坐标下的表达式为lgN=14.064 0-3.774 5lg(S-173.2)[12]。

由表1可知，当试件处于三轴向同时激励下，危险面边缘各点的疲劳寿命基本相同，约为1 492 s。文献[7]中三轴同时振动时的平均试验寿命约为620 s，计算结果与试验结果比较在2.5倍误差以内，产生误差的原因主要有以下几点：首先，试验试件在加工时可能对试件造成试验前损伤或应力集中；其次，试件的材料与理论的连续性、均匀性和各项同性存在差别；另外，在试验过程中振动台的振动控制谱与参考谱不可能保持完全一致，在控制工程中会存在瞬时的冲击。以上原因都会造成试件裂纹的加速扩展，缩短试件的疲劳失效时间。

表1　疲劳寿命与等效Von Mises应力RMS

由于Z轴振动影响可以忽略不计，由表1通过比较三轴同时激励与 x、y轴分别激励的等效应力的RMS值发现，当结构受到各轴同时激励时各点等效应力的均方等于单轴分别激励时各等效应力的均方和。即多轴向同时激励时结构上各点的应力为单轴向分别激励时应力的叠加。对于结构上一般位置，当结构受到各轴向同时激励时其叠加应力大于单轴依次激励时的应力。因此相对于单轴向激励，多轴向同时激励更容易引起结构疲劳失效。对于特殊位置，如算例中计算点1(y向振动引起的弯曲中性轴上点)，三轴同时激励与x向单独激励具有相同的疲劳寿命。

表2　各计算点单位时间的疲劳损伤

另外，危险截面边缘上的点由于处于同一圆周上，三轴向分别激励引起的应力在叠加后具有相同的等效应力均方根值，因此在三轴同时激励的工况下,危险截面边缘各点有相同的疲劳寿命，均为构件的危险点。但是，在单轴向激励时，结构的危险点仅为截面圆周与振动轴的交点(如x方向振动时计算点1)，因此结构在多轴向同时激励与单轴向激励下的失效位置是不同的。

由表2数据可知，多轴同时激励时对结构造成的损伤大于各个方向分别激励时的损伤之和。因此，不能简单的以单轴分别激励下的损伤的叠加来等效各轴向同时激励时结构的实际损伤。另外，由各计算点在各轴向同时激励损伤与单轴向分别激励损伤的损伤比可知：结构不同位置在多轴向激励下的多轴效应也是各不相同的。

4结论

(1)提出了结构在多轴向激励下疲劳寿命分析的频域分析方法，给出了该方法的计算流程。算例与实验结果比较表明，该方法满足工程需要。并且计算量小，具有一定工程应用价值。

(2)通过计算分析的可知，在各向激励载荷互不相关的加载工况下，多轴同时激励时结构上各点的应力等于单轴分别激励时应力的叠加。因此多轴同时激励时结构更容易引发疲劳失效。另外，在多轴同时激励与单轴激励下结构的失效位置一般是不同的。

(3)通过计算各点单位时间内的损伤，研究了构件受到各轴向同时激励时的多轴效应，结果显示，多轴同时激励对结构上大多数的点造成的疲劳损伤大于单轴依次振动时对该点造成的疲劳损伤之和。而且对于结构上不同位置二者之间的损伤比也是不同的，即多轴向激励下结构上各点有不同的多轴效应。因此，不能简单的采用三轴向依次激励的损伤叠加来等效多轴同时激励时产生的损伤。

(4)本文计算中没有考虑载荷谱的相关，关于载荷相关性对结构的动力响应和疲劳损伤的影响，将在今后工作中进一步研究。

参考文献

[1]Chang K Y, Frydman A M, Three-dimensional random vibration testing definition and simulation[C]// Proceedings of the Institute of Environmental Sciences,1990:129-139.

[2]Whiteman W E. Inadequacies in uniaxial stress screen vibration testing[J]. Journal of the IEST,2001,44:20-23.

[3]夏益霖.多轴振动环境试验的技术、设备和应用[J].导弹与航天载运技术，1996，6:52-59.

XIA Yi-lin. The technology, equipment and application of multi-axis vibration environment testing[J]. Missiles andSpace Vehicles,1966,6:52-59.

[4]崔旭利，陈怀海，贺旭东，等. MIMO 随机振动试验频响估计中激励和响应的同步方法[J].振动与冲击，2012,31(3)：92-96.

CUI Xu-li, CHEN Huai-hai, HE Xu-dong, et al.Synchronization between excitation and response signals in frequency response function estimation for MIMO ranom vibration test.[J]. Journal of Vibration and Shock,2012,31(3):92-96.

[5]陈颖，朱长春，李春枝，等. 典型结构在单、多轴随机振动下的动力学特性对比研究[J]. 振动工程学报，2009，22(4)：386-390.

CHEN Ying, ZHU Chang-chun, LI Chun-zhi,et al. Comparison of dynamic characteristics of a typical structure under single-axial and multi-axial random vibration loads[J]. Journal of vibration and shock, 2009, 22(4):386-390.

[6]French R M, Handy R, Cooper H L. Comparison of simultaneous and sequential single axis durability testing[J]. Experimental Techniques, 2006,30(5):32-35.

[7]Whiteman W E, Berman M S. Fatigue failure results for multi-axial versus uniaxial stress screen vibration testing[J].Shock and Vibration,2002,9:319-328.

[8]金丹，陈旭.多轴随机载荷下的疲劳寿命估算方法[J].力学进展，2006，36(1):65-74.

JIN Dan, CHEN Xu. Fatigue life evaluation under multiaxial random loadings[J]. Advances in Mechanics, 2006，36(1):65-74.

[9]Benasciutti D, Tovo R. Comparison of spectral methods for fatigue analysis of broad-band Gaussian random processes [J]. Probabilistic Engineering Mechanics, 2006,21:287-299.

[10]Dirlik T. Application of computers in fatigue analysis[D]. University of Warwick, UK,1985.

[11]Paulus M, Doughty K. Effect of resonant frequency shifting on time to failure of a cantilevered beam under vibration [J]. Journal of the IEST,2010,53(1):59-68.

[12]中国航空材料手册，第三卷：铝合金，镁合金[M].北京：中国标准出版社，2002.