基于同源数据的序列比例尺地图综合缩编平台建设

刘　洋,兰泽英

(1.广州市城市规划勘测设计研究院，广东广州510060；2.广东工业大学管理学院，广东广州510060)



基于同源数据的序列比例尺地图综合缩编平台建设

刘洋1,兰泽英2

(1.广州市城市规划勘测设计研究院，广东广州510060；2.广东工业大学管理学院，广东广州510060)

摘要：如何维护更新数据是“数字城市”建设中面临的重要问题，而构建基于同源基本大比例尺数据连续化生产序列小比例尺数据，对多尺度城市空间数据进行纵向一体化管理的软件平台成为数据更新维护的关键。研究以基于同源数据的序列比例尺地图综合缩编平台建设为对象，主要从地图综合知识库形式化表达、地图综合流程决策控制机制、构建开放式地图综合软件系统构架体系、高效地图综合算子设计等方面进行重点阐述。此研究建设的软件平台已在广州市大型多尺度空间数据库快速构建中得到成功应用。

关键词：多尺度空间数据库；同源数据；序列比例尺；地图综合；数据更新

在“数字城市”建设中，完成基本比例尺地图数据建库后，面临的重要问题就是如何维护更新数据，以及建立跨比例尺数据间的联系，使得不同比例尺数据库形成一个整体化、一致性、鲜活性的数据资源[1]。数字技术环境下的自动化地图综合技术成为必须解决的关键技术问题[1]。

广州市经过数年的信息化建设，面向城市规划建设管理的基础信息设施已初具规模,目前面临的重要问题是：数据库的尺度难于协调，难于形成跨比例尺间的数据转换。究其原因有二：一是在于目前的空间数据基础设施建设缺乏多尺度数据库处理工具，缺乏一种技术平台将不同尺度的数据统一起来；二是目前地图综合技术的研究成果大多集中在中、小比例尺地图综合或两个特定尺度的地图综合，而在大比例尺的城市地图综合技术方面研究较少，且大比例尺地图综合存在着数据模型对实体世界的抽象概括程度不够、地图意义识别困难、人造地物结构及分布特征复杂等诸多难点[2]，需要开发一些适用性很强的综合算子。

在此背景下，本文旨在研发基于同源基本大比例尺数据连续化生产序列小比例尺数据，对多尺度城市空间数据进行纵向立体式管理的统一软件平台。本文从3个层面进行重点阐述，首先建立地图综合规则的六元组形式化表达机制和五因素综合流程控制机制，然后构建开放式地图综合软件系统构架体系，最后针对广州地区序列比例尺地图综合特征开发一些适用性强、高效率的综合算子。

1建立地图综合规则库及决策推理机制

1.1　构建六元组形式化表达的地图综合规则库

采用计算机实现综合过程，首先要对地图综合规则知识的研究建立形式化描述机制，本文对综合规则通过形式化处理表达为六元组[3]，其元素包括数据处理对象的要素类别、属性标识、几何算法、控制指标、指标的适用上限、适用下限。

(〈层代码〉，〈操作算子〉，〈属性码〉，〈指标项〉，〈下限〉，〈上限〉)

该六元组的通用意义可表达为：当〈层代码〉内的目标具有〈属性码〉，且其〈指标项〉小于〈上限〉且大于〈下限〉时，执行〈操作算子〉。

1.2　建立多因素的综合流程决策推理机制

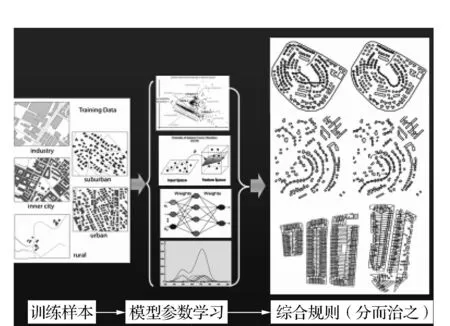
图1　综合知识规则库建立图

在决策推理中，本文建立5因素的综合流程控制机制[3]，包括激活数据层、要素类型、比例尺变化范围、用户操作消息、几何控制指标。在系统实现中针对不同比例尺、不同专题、不同用途的数据综合工程任务，由机器学习、地图综合缩编的图式规范及综合经验的总结等多种途径建立综合知识规则库(见图1)、设定规则参量，完成综合工作环境的建立。软件系统实现中，为地图综合过程的决策推理建立一定的约束条件，具体参见文献[3]。

2构建开放式地图综合软件系统构架体系

本文建立开放的、可扩充的系统构架，系统结构设计为三层圈层式结构[3]，由内而外分别为数据库管理平台、综合算子综合环境以及缩编工程应用扩展(见图2)。

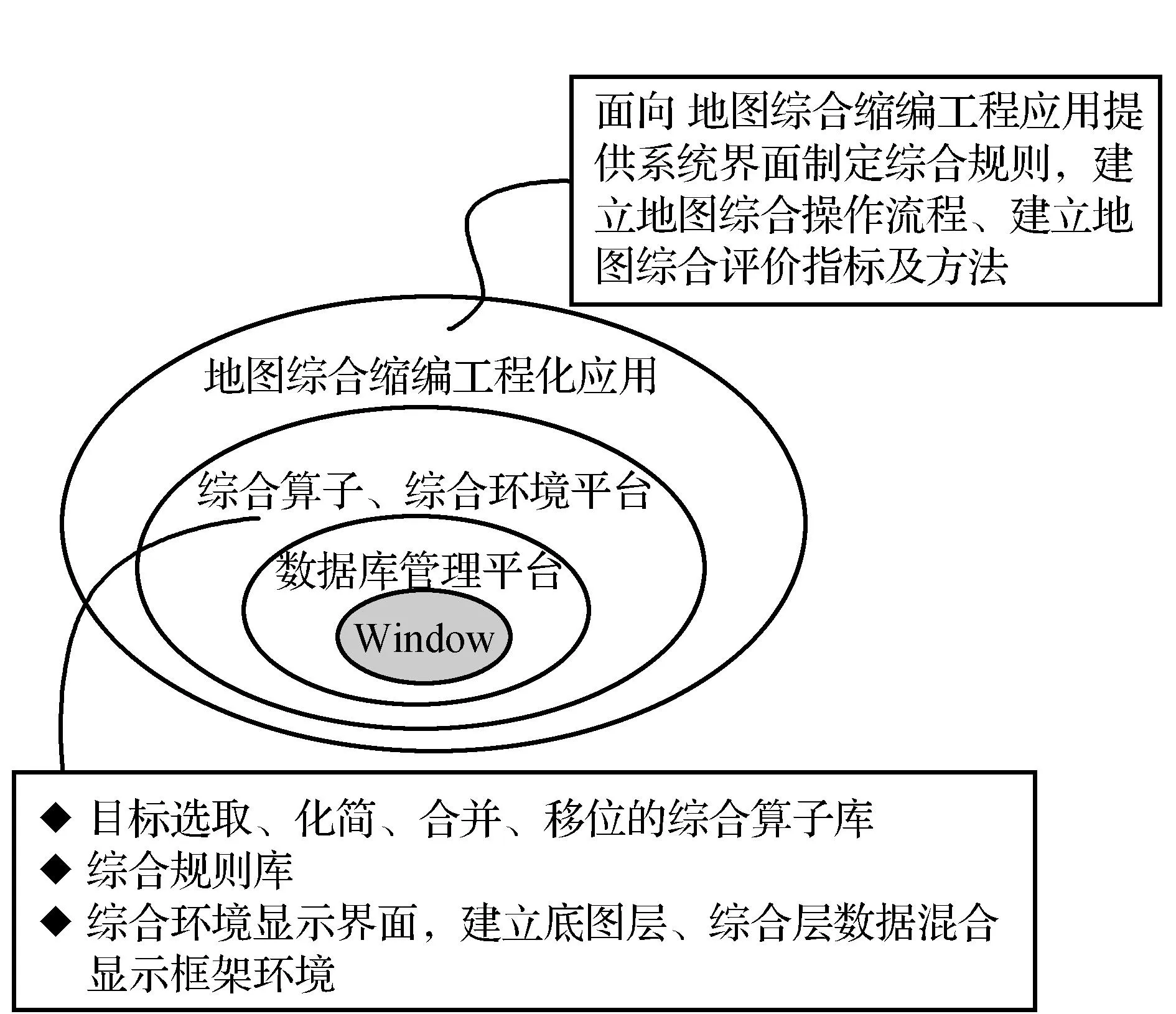
图2　软件三层圈层式构架

三级圈层式结构越向外，越面向工程应用，最里层的数据库平台由ArcGIS平台提供数据的读取、组织、基本属性编辑或几何编辑、可视化表达及输出存储等相关基本空间数据处理接口，并可以结合综合算子开发地图数据综合处理功能，在此基础上定制面向综合的可视化环境、综合规则及综合参数设置等。第二层综合算子和综合环境的建立，根据地图综合算子、面向综合的数据模型，设计研制一批实用的通用型地图综合算子组件，对于具有特殊地理空间分布模式的要素综合还需在此基础上开发一些适用性强且高效的综合算法。第三层地图缩编工程应用，通过多种综合算子的组合完成面向现有数据库的综合过程开发。系统采用后台要素层次批量综合处理与前台目标层次交互式综合处理相结合的综合方式。

3关键性综合算子设计

除了通用型地图综合算子组件，本研究在Voronoi图、Delaunay三角网模型上对算子设计作深入探讨，开发适用性很强的综合算子。

3.1　保持路网密度的道路选取算子

道路选取资格综合考虑多个指标，包括道路等级、局部路网密度、道路stroke长度、道路stroke连通性[4]。具体算法如下, 算法时间复杂度为O(nlogn)，空间复杂度为O(n)。

1)生成道路中心线弧段：采用“骨架线”提取算法生成道路区域的骨架线网络[5]，对骨架线进行平滑、化简和数据预处理(断线连接，删除伪结点、悬挂线、短线等)，生成道路中心线弧段网络，基于微积分思想加权累积计算获取每个弧段的平均宽度[6]，并计算其长度；

2)道路中心线弧段stroke连接：即判断拓扑关联的弧段是否属于同一stroke的过程，一般综合考虑弧段间的方向一致性和语义一致性进行判断[4]，本文采用的连接策略是以方向一致性判断为主，辅以街道名称来判断(若为无名路则不考虑语义一致性)。设道路中心线弧段ei和ej，它们可划分为同一stroke进行连接的条件是：ei和ej具有公共结点p，且ei和ej的方向夹角θij(取锐角)小于阈值δ(一般根据试验结果确定，本文取值60°)，连接效果如图3a所示。 θij越小，ei和ej的连通延展性越好，θij为0时，两者方向完全一致。然后计算同一组弧段的平均宽度和总长度作为stroke的宽度和长度。

3)道路中心线弧段stroke分级：本文主要综合考虑stroke的宽度和长度对其进行分级，判定标准如下：若stroke宽度和长度均满足当前等级I阈值要求时，直接设定其等级为I；若宽度达不到阈值要求，则直接与下一等级比较；若宽度满足要求，长度不够时，则直接设定其等级为I-2。计算机自动分级后局部不合理之处需人工调整。

4)顾及道路目标stroke特征保持的路网自动综合：本文采用文献[4]提出的综合算法， 首先依据方根模型确定道路的选取比例，采用约束Delaunay三角网构建道路中心线弧段的邻近关系模型，然后按如下算法对路网进行迭代抽稀(图3b中的黑色弧段为要删除抽稀的弧段)：①锁定高等级道路；②删除最短没有被锁定且删除后不影响连通性的道路R(如图3c圈中的弧段为影响连通性的关键弧段，具体判断方法见文献[4])；③锁定R周围的道路；④如果达到选取比例则终止，否则到⑤；⑤如果所有道路都被锁定则解锁所有低等级道路，并跳至②。本算法不仅可兼顾个体目标重要性和保持路网密度分布特征，还将动态维护路网的连通性[4]。基于本算法的综合效果如图4所示。

图4　道路选取效果

3.2　顾及居民地分布特征的建筑物综合算法

随着尺度由大变小，建筑物要素依次呈现为单幢房屋、建筑群组、建筑区域以及街区等不同粒度，综合效果如图5所示。且大尺度转换时对空间数据的几何精度要求较高，建筑物综合大多表现为合并、化简和选取；而中小尺度转换对几何精度要求降低，为保持地图可视化的美观，除包括以上的综合操作外还会涉及建筑物间隙等宽化处理、建筑群移位处理等操作。而建筑物多边形分组合并方法是其中的关键问题。

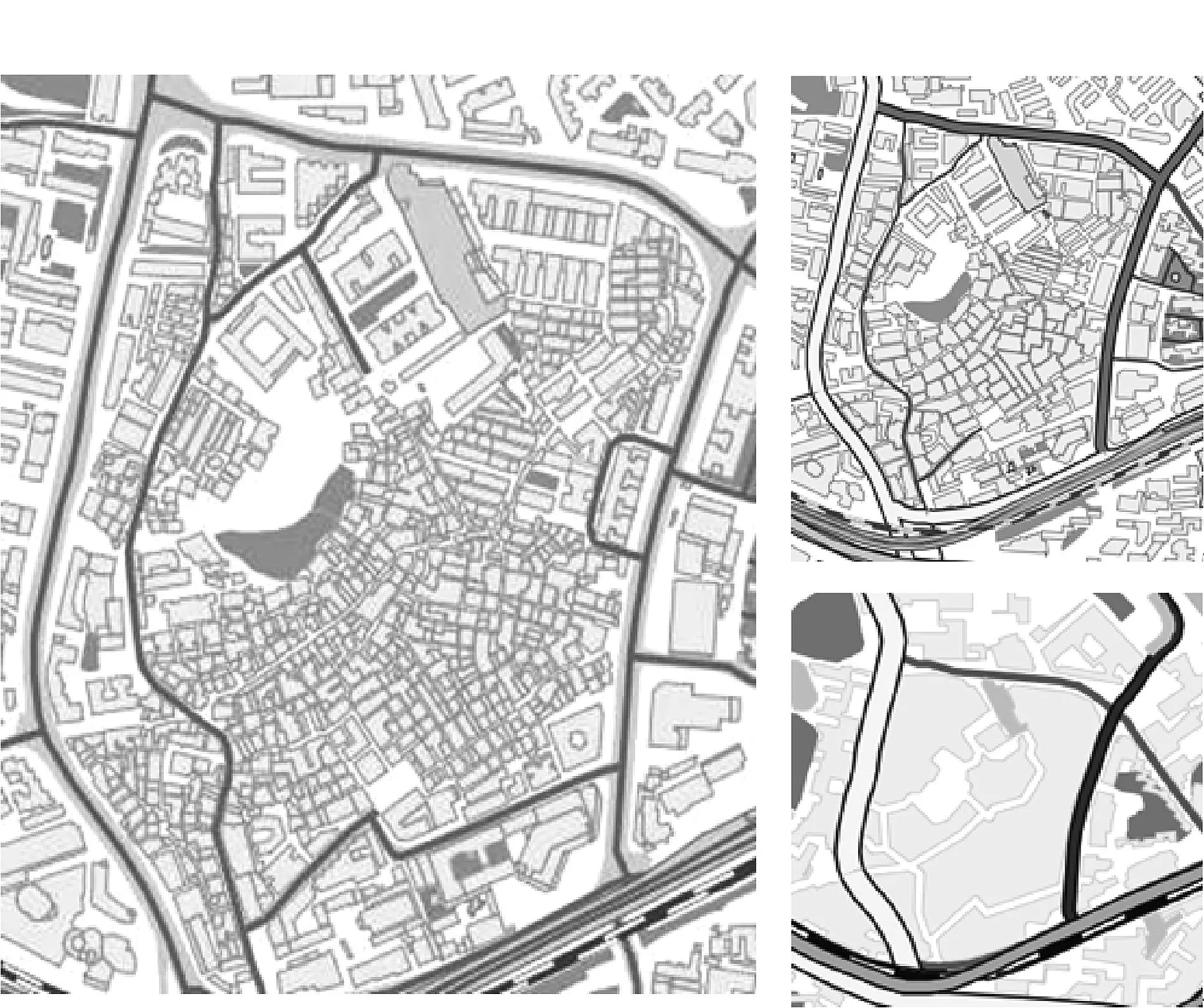
图5　序列比例尺建筑物综合效果

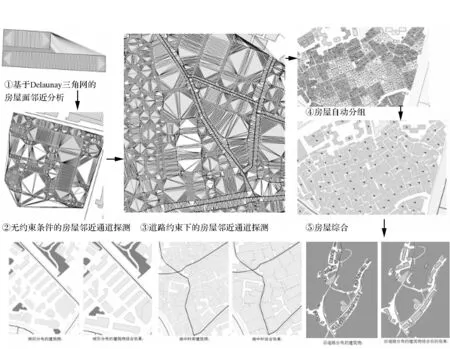
图6　邻接相关边探测及建筑物分组流程示意

3.2.1　建筑物多边形的分组合并算法

图6展示了邻接相关边探测及分组合并的流程。邻接相关边是基于建筑物群的约束Delaunay三角网空间剖分模型以及邻接跨立三角形判定为基础来定义的[6]，它构成建筑物目标间的“邻近通廊”，具体如下：

1)采用Delaunay三角网建立建筑物群的空间剖分模型：为避免建筑物边界与三角形相交以及三角形穿越道路，本文采用约束Delaunay 三角网，参加三角网构建的点为建筑物边界及道路中心线上的端点和内插点，内插步长为相邻建筑物间的最小距离阈值。

2)确定多边形间的邻接跨立三角形：剔除位于多边形内部或其凹部区域的三角形，仅保留跨立三角形(即两个节点在同一个要素上，另外一个节点在另一个要素上的三角形)。设跨立三角形位于同一要素上的边为底边，其他两边为腰，排除任意一条腰长度超过距离阈值的三角形，排除腰与底边形成的夹角中任意角度超过阈值θ(经验取值，本文取值100°)的三角形，剩下的即为多边形间的邻接跨立三角形。

3)计算多边形间的邻接相关边长度：多边形间所有邻接跨立三角形底边的集合即为多边形间的邻接相关边，所有邻接跨立三角形底边长度之和即为多边形间的邻接相关边长度。

建筑物分组合并时，将采用建筑多边形间平均距离、建筑多边形间邻接相关边长度以及建筑分组面积等3个指标作为控制指标。其中距离控制建筑物分组资格，只有建筑物距离小于阈值时才能分为一组；邻接相关边长度控制分组决策过程，优先合并邻接相关边长度最长的两个建筑多边形；建筑分组面积控制分组停止条件，即综合的粒度，当分为一组的多边形总面积超过阈值(缩编后最小上图面积)时，此组多边形将丧失“活性”，不再参与合并。建筑物分组的具体过程如下：

1)计算每个建筑物多边形的面积并排序，面积大于缩编后最小上图面积的多边形将丧失“活性”不再参与分组操作，取面积最小的“活跃”多边形A作为当前目标；

2)在Delaunay三角网建立的建筑物群的空间剖分模型中考察与A有邻接跨立三角形联系的建筑物多边形集U，获取与A平均距离在阈值以内的建筑物多边形集U′，取U′中与A邻接相关边长度最长的建筑物多边形B与之优先分为一组(当邻接相关边长度相同时，考虑平均距离较小的多边形)；分组后的多边形集将作为一个完整的大多边形参与面积计算、排序和分组操作；

3)返回步骤1；

4)直至所有多边形均丧失“活性”，分组操作停止。

对于城区规则排列建筑物群，以上算法效果较理想。对于城中村不规则排列建筑物群，则需采用“先路网生成处理，后建筑分组合并”的迂回策略；对于郊区具有方向延展性的建筑物群，应采用方向差异权值对目标间邻接相关边长度进行修正，将方向因子纳入视觉邻近关系计算中[6]。

3.2.2建筑物的选取、化简、间隙等宽化处理及冲突移位

对于花都、从化、增城等山区随机分布的散列式居民地，本文首先采用Collapse算法将散列式居民地从几何特征上由二维转变为0维的点和1维的线，然后采用基于Voronoi图的群点重采样算法进行化简和选取[7]，见图7a。

基于计算几何的建筑物化简方法一般有矩形拟合、字母形状匹配法、边界最小二乘拟合、缓冲区扩后再收、弯曲化简等5种方法，其中前3种方法主要针对房屋类型多边形，后两种针对街区类型多边形[8-12]，如图7b所示。本文采用弯曲化简方法[11-12]，即在Delaunay三角网建立的建筑物群的空间剖分模型，依次对每个建筑物在保持邻近关系的情况下，删除小的弯曲，保持建筑物形状，并维持建筑物直角化特征，达到化简建筑物的效果。

建筑物要素综合到中比例尺，如1∶25 000时，为了图面美观，需要对建筑物区域间的缝隙做等宽化处理。首先构建每个街区中建筑物群的凸壳，提取凸壳中非建筑物的“背景”区域；基于Delaunay三角网提取“背景”区域的骨架线；以骨架线为中轴，按一定宽度构建缓冲区，形成新的“背景”区域；将新“背景”区域与凸壳做空间叠置即可达到等宽化处理效果，见图7c。

建筑物群的冲突移位处理主要采用基于场论原理的街道、建筑物保持拓扑一致的移位处理[13-15]，即结合Delaunay三角网和Buffer分析探测邻近冲突部位，基于场论原理，通过邻近度和邻近分析的计算决定目标移位的方向和距离，如图7d和图7e所示。

3.3　水系要素综合算法

水系综合主要包括双线河变单线河、水域毗邻化处理、水域多边形合并、线状河流化简、水系网选取以及沟渠处理等。植被要素的综合处理以选取、合并及化简为主，其处理方法与水域多边形有类似之处，本文不再赘述。

双线河变单线河、水域毗邻化处理的基本算法均为骨架线提取的中轴化算法[5]，其中水域毗邻操作的实现是在邻近湖泊多边形间隙空白区域提取骨架线，沿着骨架线将多边形边界缝合，犹如穿衣服“拉上拉链”[3]，见图8a。水域多边形的合并也基于约束Delaunay三角网的空间剖分模型来探测相邻多边形的邻近部位，进行合并，水域合并需要考虑一定的约束条件，如不能穿越沟渠、线状河流等[12]。线状河流化简则在矢量点压缩的基础上，利用Delaunay三角网建立弯曲层次结构，删除小弯曲，保持总体形态轮廓,达到线化简的目的[11]，见图8c。

水系网的选取抽稀主要基于Horton法则建立水系网的平面结构树和语义层次树(见图8b)，并由线到面基于Delaunay三角网建立各河流分支汇水区域的层次化剖分，进而通过该剖分结构进行水系树的化简[16]。此外，广州地区的水系分布有其特殊性，尤其是南沙区，河网密集、沟渠众多、分布规则，本研究采用基于数学形态学的算法进行沟渠选取(见图8d)，分4个步骤进行处理：中轴化沟渠骨架线提取、侵蚀算法沟渠与河流分离、沟渠抽稀、膨胀算法沟渠与河流挂接等。

3.4　基于加权群点重采样算法的POI点选取

采用基于重要性程度(POI点级别)的加权Voronoi图的点群选取化简算法实现POI点综合[7]，具体思想如下：①利用POI数据生成Voronoi图；②根据每个点所占的面积乘以点的权重，得到每个点的重要度；③剔除重要度最低的点，同时锁住周围的点；④剔除未被锁住的重要度最低的点，同时锁住周围的点；⑤重复④直到达到剔除比例，选取完成；或剩下所有的点都被锁住，解锁所有点，转至③。

3.5　多要素综合结果的空间一致性维护

导致空间一致性关系破坏的原因包括数据来源于不同比例尺、分要素独立化简综合、综合过程中的几何维数变化等。依据维护对象的类型，综合关系维护可以分为同要素类一致性维护和不同要素类间的一致性维护[17-18]。而空间数据处理主要基于Delaunay三角网模型邻近分析探测由三角形集表达的边界不一致局部区域，通过三角网骨架线提取来进行边界不一致改正，过程如图9所示。

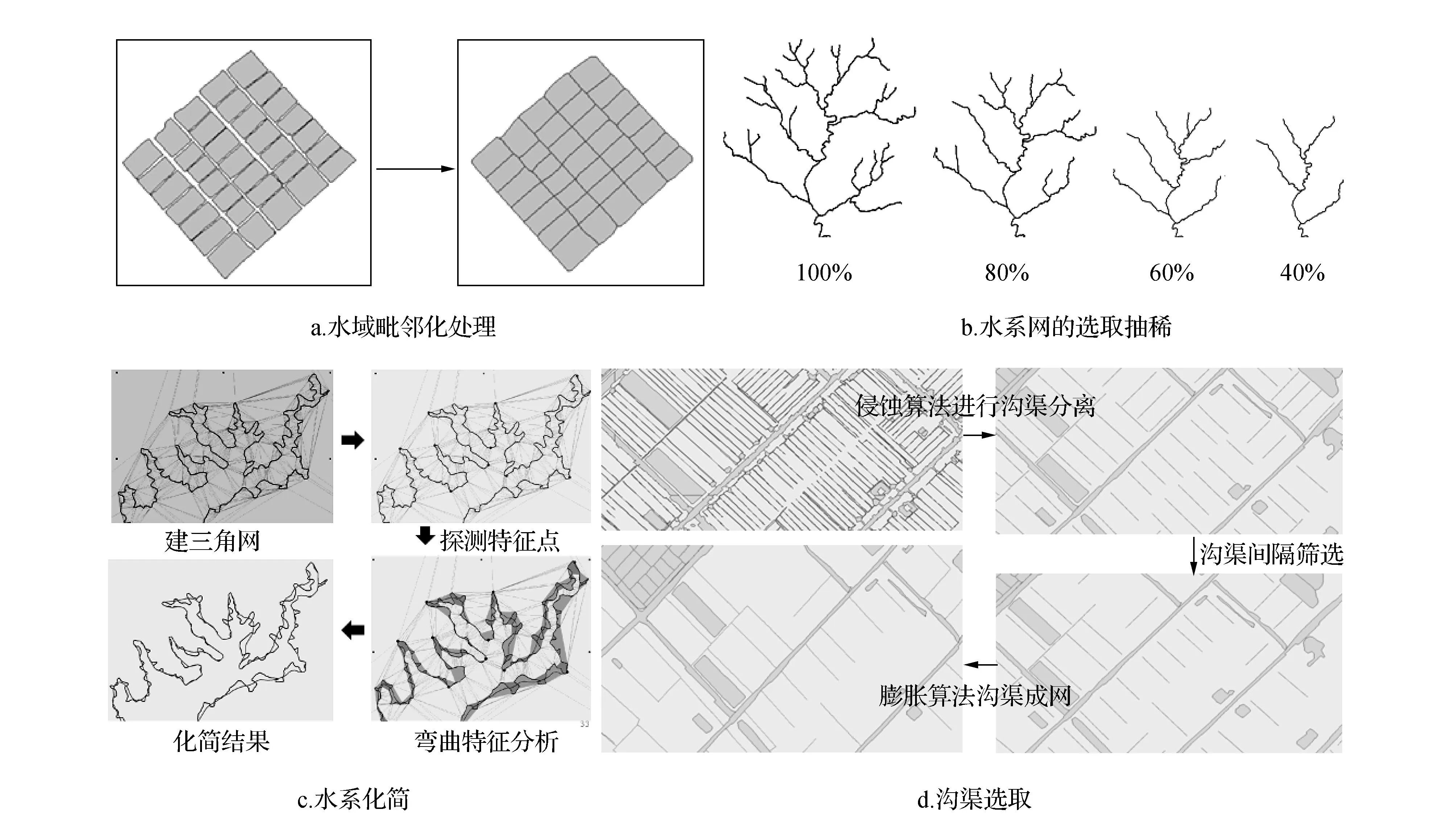
图8　水系综合处理

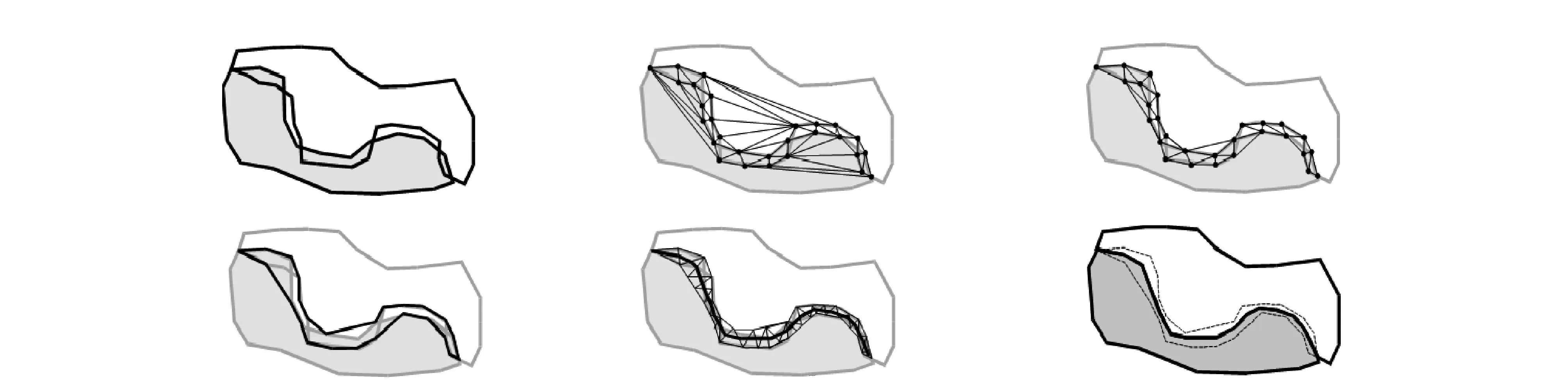
图9　边界不一致维护流程

4应用

依托广州市基础地理信息数据库，通过数据抽取、重构及规范化、一致性处理生成本底地理基础框架数据库，并将其作为同一母版数据资源，采用本文开发的“基于同源数据的序列比例尺地图综合缩编平台”，快速构建广州市纵向立体化生产及管理的多尺度地理基础框架数据(包括1∶2 000、1∶1万、1∶2.5万、1∶5万、1∶10万、1∶20万及1∶50万等7个数据尺度)，并以此为基础叠加约80万条门牌及门楼址、约20大类22.5万条POI记录专题数据，从而首次构建具有独立知识产权，涵盖广州市全市域约7 400 km2的大型多尺度空间数据库。

本研究构建的广州市多尺度空间数据库成果，在面向公众及政务的在线式地理信息服务、专业GIS系统开发以及基于GIS数据的需求适应型专题地图快速编制研究方面进行应用，取得显著社会效益和经济效益。

5结束语

本文针对“数字城市”建设中如何保证多尺度数据资源的快速更新及一致性维护这一关键技术开展研究，研发基于同源大比例尺数据连续化生产序列小比例尺数据、对多尺度城市空间数据进行纵向立体式管理的统一软件平台,开发“人性化”的、人机协同的高效交互式数据综合工作模式，通过工日测算生产效率比传统方式提高6倍以上。

本文突破本领域一直存在的地图综合理论研究与工程化应用相脱离的局面。基于人工智能知识规则表达机制，构建六元组的地图综合规则库形式化描述机制及五因素的综合流程决策推理机制；研发开放式地图综合软件系统构架体系；针对广州市交通网络密集、河网水系发达且分布形态多样、居民地密度不均且分布模式各异的独特地理特征，开发一批适用性很强的高效综合算子，突破从写真式大尺度到抽象式中小尺度的序列比例尺地图综合的诸多技术难题。对快速构建或更新城市多尺度空间数据库具有重要借鉴意义。

参考文献：

[1]艾廷华，成建国.对空间数据多尺度表达有关问题的思考[J].武汉大学学报(信息科学版),2005,30(5):377-382.

[2]郭仁忠，艾廷华.制图综合中建筑物多边形的合并与化简[J].武汉测绘科技大学学报,2000,25 (1):25-29.

[3]艾廷华，郭宝辰，黄亚峰.1∶5万地图数据库的计算机综合缩编[J].武汉大学学报(信息科学版),2005,30(4):297-300.

[4]杨敏，艾廷华，周启.顾及道路目标stroke特征保持的路网自动综合方法[J].测绘学报,2013,42(4):581-587.

[5]艾廷华，郭仁忠.基于约束Delaunay结构的街道中轴线提取及网络模型建立[J].测绘学报,2000,29(4):348-354.

[6]艾廷华,郭仁忠.基于格式塔识别原则挖掘空间分布模式[J].测绘学报,2007,36(3):302-308.

[7]艾廷华，刘耀林.保持空间分布特征的群点化简方法[J].测绘学报,2002,31(2):175-181.

[8]刘鹏程,艾廷华,邓吉芳.基于最小二乘的建筑物多边形的化简与直角化[J].中国矿业大学学报,2008,37(5):699-704.

[9]艾廷华，帅赟，李精忠.基于形状相似性识别的空间查询[J].测绘学报,2009,38(4):356-362.

[10]刘鹏程，艾廷华，胡晋山，等.基于原型模板形状匹配的建筑多边形化简[J].武汉大学学报(信息科学版),2010,35(11):1369-1372.

[11]艾廷华，郭仁忠，刘耀林.曲线弯曲深度层次结构的二叉树表达[J].测绘学报,2001,30(4):343-347.

[12]艾廷华，郭仁忠，陈晓东.Delaunay三角网支持下的多边形化简与合并[J].中国图像图形学报,2001,6(7):703-708.

[13]艾廷华.Delaunay三角网支持下的空间场表达[J].测绘学报,2006,35(1):71-82.

[14]周启，艾廷华，张翔.面向多重空间冲突解决的移位场模型[J].测绘学报,2013，42(4):615-620.

[15]孟妮娜，艾廷华，周校东.建筑群邻近关系相似性计算[J].武汉大学学报(信息科学版),2012,37(7):775-778.

[16]艾廷华，刘耀林，黄亚锋.河网汇水区域的层次化剖分与地图综合[J].测绘学报,2007,36(2):231-236.

[17]李精忠，艾廷华.多尺度土地利用数据库构建过程中的拓扑一致性维护[J].测绘通报,2011(8):32-35.

[18]艾廷华，刘耀林.土地利用数据综合中的聚合与融合[J].武汉大学学报(信息科学版),2001,30(4):486-492.

[19]蒙印,艾廷华，杨井源.1∶250 000水系要素综合缩编技术方法[J].测绘与空间地理信息，2014，37(3)：201-203.

[20]王亮，吴艳兰，汤军，等.改进的双向缓冲海岸线综合方法研究[J].测绘科学，2015,40(1)：18-21.

[21]詹金瑞，何华贵，陈飞，等.城市多尺度数据的地图综合技术研究[J].测绘科学，2015,40(1)：18-21.

[22]程辉，唐南奇，唐亮.基于Model Builder中心线提取建模的制图综合研究[J].测绘与空间地理信息，2014，37(5)：81-84.

[23]夏永亮.基于复杂网络理论的城市道路网络自动综合方法[J].测绘与空间地理信息，2014，37(8)：155-156.

[责任编辑：张德福]

《测绘工程》网上投稿系统正式开通试用

《测绘工程》编辑部为提高稿件处理的网络化水平和采编工作的效率,及时让作者了解稿件的处理情况,自2015年7月1日起网上投稿系统正式开通试用,可实现作者网上投稿、实时查询稿件状态及修改意见,专家网上审稿以及编辑网上处理稿件等功能,使稿件审理愈加快捷、方便、有效。

1)直接登录《测绘工程》网上投稿系统单独域名http://xsqk.hljit.edu.cn/Jweb_chgc

2)登陆http://www.hljit.edu.cn进入黑龙江工程学院主页，然后进入编辑部二级网页，然后点击投稿指南中的网址链接或《测绘工程》封面,即可登录到投稿系统。

审稿专家在收到编辑部的送审邮件中直接点击相关链接即可开始审稿，另外也可通过上述方式进入系统，使用编辑部提供的账号和密码(登陆后，审稿专家可自行修改个人信息)点击网站左侧的“专家审稿”可进行审稿操作。

2016年1月1日后，在线投稿系统正式运行，《测绘工程》原投稿邮箱(E-mail:chgc2008@vip.163.com)将不再接收任何投稿。

联系电话:0451-88028906/88028496

编辑部联系邮箱:chgc2008@vip.163.com

(本刊编辑部)

The software platform of sequence scale map generation based on same homologous data

LIU Yang1,LAN Ze-ying2

(1.Guangzhou Urban Planning & Design Survey Research Institute,Guangzhou 510060,China；2.Guangdong University of Technology,Guangzhou 510060,China)

Abstract：The critical problem in digital city construction is how to update the multi-scale spatial data timely and consistently.This paper purposes a software platform of sequence scale map generation based on the same basic large scale data,which can also provide unified and longitudinal vertical management of multi-scale data.The study includes three main parts.Firstly,it sets up a six-element formal expression of map generation rules,and then builds a five-factor control mechanism of map generation process.Secondly,it constructs a open system architecture for the software platform of sequence scale map generation.Thirdly,it studies a series of applicable and efficient map generation algorithms considering the unique geographical features in Guangzhou city.The software platform has been successfully applied to the rapid building of multi-scale spatial database in Guangzhou City.

Key words：multi-scale spatial database；same homologous data；sequence scale；map generation；data updating

作者简介：刘洋(1981-)，男，博士.

基金项目：国家自然科学基金青年科学 (41301377)

收稿日期：2015-01-22；修回日期：2015-02-01

中图分类号：P208

文献标识码：A

文章编号：1006-7949(2015)12-0036-07