基于TLS的多变量灰色模型在大坝变形预报中的应用

卢辰龙，匡翠林，陈晓林，鲁鹤松

(1.中南大学地球科学与信息物理学院，湖南长沙410083;2.郑州市市政工程勘测设计研究院,河南郑州450000;3.中南勘测设计研究院有限公司，湖南长沙410014)



基于TLS的多变量灰色模型在大坝变形预报中的应用

卢辰龙1,2，匡翠林1，陈晓林1，鲁鹤松3

(1.中南大学地球科学与信息物理学院，湖南长沙410083;2.郑州市市政工程勘测设计研究院,河南郑州450000;3.中南勘测设计研究院有限公司，湖南长沙410014)

摘要：传统多变量灰色模型MGM(1,n)的背景值误差会使得求解的灰色参数精度降低。总体最小二乘是一种可以同时顾及到观测误差与模型系数矩阵误差的数学方法。基于此，引入TLS对传统MGM(1,n)模型的灰色参数进行修正。通过对某大坝变形数据试算，验证表明，该方法能够有效地提高变形预报精度。

关键词：大坝变形预报；多变量灰色模型；背景值优化；总体最小二乘

大坝在供水、能源、航运供给以及防洪等方面起着重要的作用，为社会经济的快速发展保驾护航，而大坝的贡献是建立在良性运行的基础之上，因此，对大坝开展安全监测工作具有重要意义[1]。为了提高大坝水平位移预报的精度与可靠性，国内外学者展开了广泛的研究并取得了一些有益的成果。目前，对大坝水平位移预报主要有神经网络法[2-4]、时间序列分析法[5]、灰色预测法[6-11]，支持向量机法[12-13]等。但上述方法大部分都是采用单点数据进行建模与预报，并未考虑不同监测点之间相互联系。但在实际中，每个监测点的变形并不都是孤立的，而是彼此间相互作用、相互影响。基于此，翟军在单点GM(1,1)模型的基础上，将其扩展为多变量灰色模型[14-17]。由于灰色模型参数直接影响模型的拟合与预报精度，而背景值又是影响灰色模型参数精度的关键因素，但传统MGM(1,n)模型的背景值的构造仍采用单点GM(1,1)模型背景值的方法，因此，对于数据序列急剧变化时，其模型预报误差较大。针对这一问题，不同学者提出了不同的背景值构造方法，提高模型拟合与预报的精度，如动态定权法[18]、向量连分式理论法[19]、非齐次指数函数拟合法[20-21]等，但上述背景值优化方法并不能保证对所有情况都适用。为此，本文在计算灰色模型参数时，考虑到由背景值求解得到的灰色参数存在误差，引入TLS[22-23]对其进行求解，并通过对湖南省某大坝实测数据计算表明，该方法的预报精度优于传统的MGM(1,n)模型与优化的MGM(1,n)模型。

1MGM(1,n)模型建立与背景值误差分析及优化

1.1　传统MGM(1,n)模型的建立

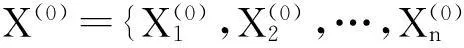
(1)

(2)

式中：j=1,2,…,m；i=1,2,…,n。

顾及到n个引张线点相关影响，对生成序列建立n元一阶常微分方差组：

(3)

将式(3)写成矩阵形式：

(4)

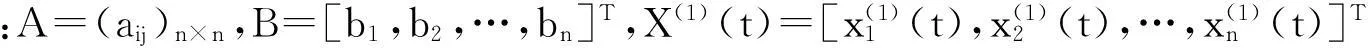
式(4)的时间响应式为

(5)

将式(4)离散化可得灰色微分方程为

(6)

其中

(7)

式中:i=1,2,…,n；k=2,3,…,m。

根据最小二乘法计算多变量灰色模型的参数A与B，

(8)

其中

(9)

(10)

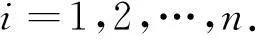
(11)

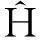
MGM(1,n)模型的时间响应函数为

(12)

将式(12)做累减还原，其模型为

(13)

1.2　背景值的误差分析

在区间[k-1,k]上对式(4)中n个白化方程进行积分可得

(14)

化简可得

(15)

式中：i=1,2,…,n，k=2,3,…,m。

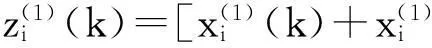
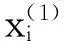
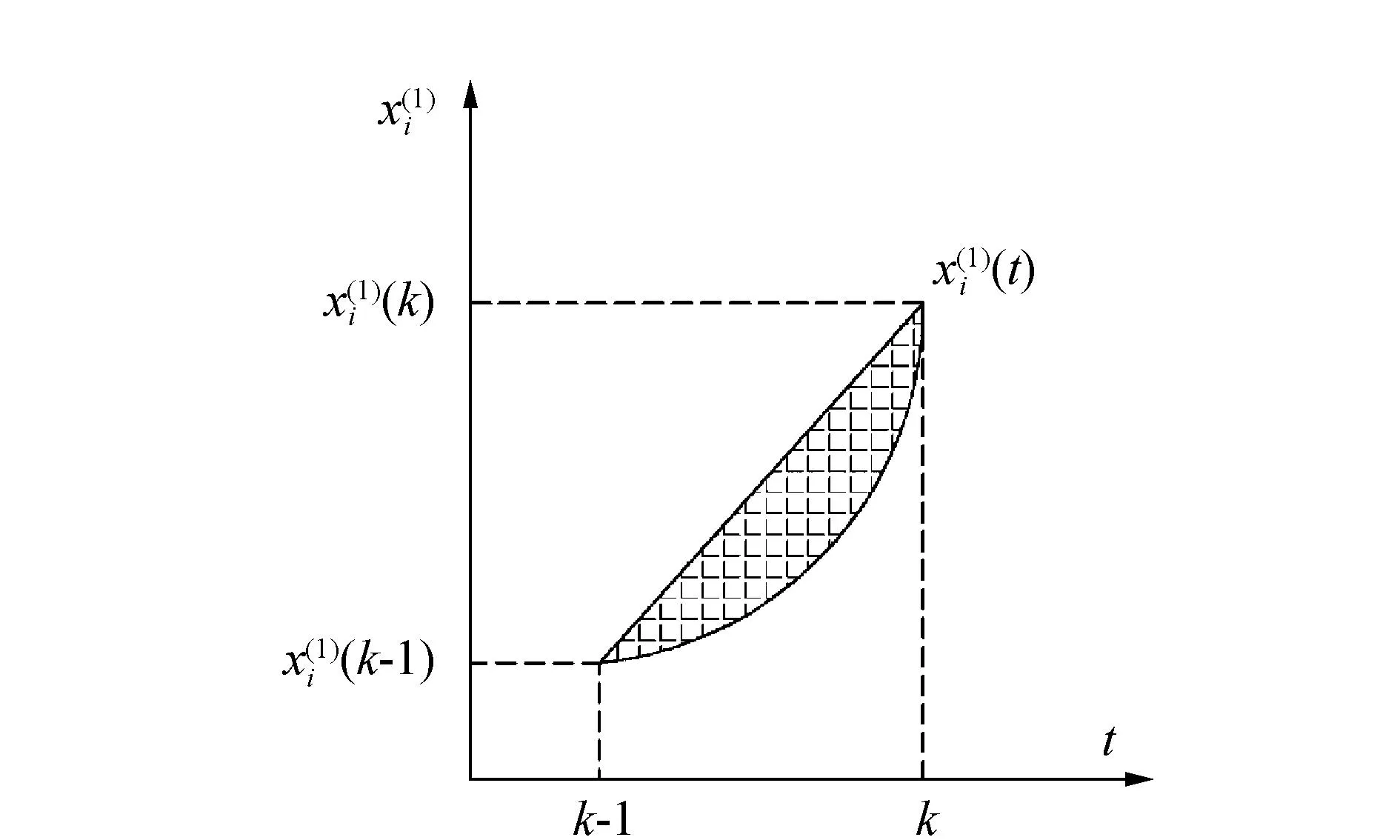
图1　第i个变量的传统背景值误差来源

2基于TLS的MGM(1,n)模型及预报精度评价指标

2.1　TLS迭代解算

在TLS[24]中，求解MGM(1,n)模型灰色参数的函数模型为

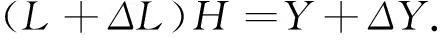
(16)

式中:ΔL为系数矩阵中存在误差，ΔY是观测误差，其误差方程式的形式为

(17)

而误差方程式(17)表示为

(18)

(19)

(20)

于是TLS的目标函数

vec(EL)Tvec(EL)+eTe=min.

(21)

等价于

(22)

求解目标函数的自由极值得

(23)

转置整理得

(24)

将式(19)与式(20)代入式(24)得

(25)

(26)

将式(19)代入式(26)整理，得到参数的估值为

(27)

式(25)可以通过迭代解算得到参数估值，计算步骤如下：

根据上述的迭代解算，即可得到参数的估值。

2.2　预报精度评价指标

为验证模型的预报结果是否可靠与稳健，分别选用平均相对误差E、均方差比值C以及小误差概率P三种指标进行评价，三种指标的定义如下：

1)平均相对误差E，E反映了预报残差占原始数据的平均比例，因此，E越小越好，其定义如下：

(28)

2)均方差比值C，越小越好，因为指标C反映了原始数据离散程度大，而残差离散程度小，

(29)

其中,S1是原始序列的标准差，S2是残差序列的标准差，原始序列与预报序列的差值序列称为残差序列。

3)小误差概率P，指标P越大越好，残差与残差均值之差小于给定值，

(30)

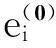
表1　模型精度评定标准

3实例分析

为验证本文算法的有效性与可靠性，以某大坝三个引张线点上14期的径向水平位移数据为例，分别选用传统MGM(1,3)模型、背景值优化的MGM(1,3)模型以及TLS-MGM(1,3)模型进行模拟预报。表2是14期的观测数据，以10 d为一个周期。

图2是以前11期数据进行建模，后3期数据用于检核，其图2中(a)、(c)与(e)分别与表2中的点A、B、C相对应，图2中(b)、(d)与(f)分别是其相对误差。从图2中可以明显看出，背景值优化的

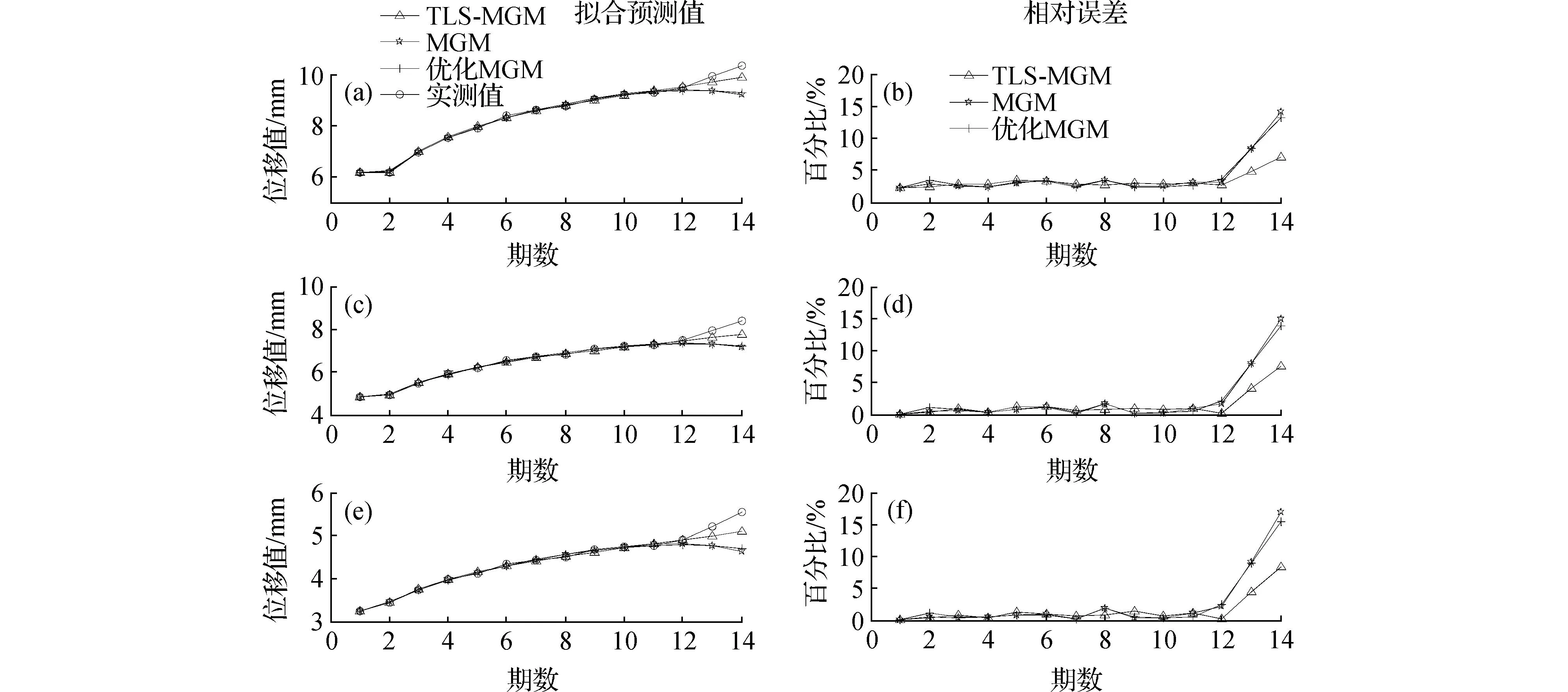
图2　不同模型的拟合预报值与相对误差

MGM(1,3)模型的预报精度并未显著提高，而是与传统MGM(1,3)模型的预报精度基本相当，而TLS-MGM(1,3)模型的预报精度则明显优于上述两种模型。为进一步说明本文方法的可靠性，又采用不同的指标进行多角度的评价，其结果如表3所示。从表3中可以看出，不同指标的结果均能明显地反映出TLS-MGM(1,3)模型优于另外两种模型。综合上述实例数据分析表明，TLS改进MGM(1,3)模型可以削弱多变量灰色模型的背景值误差，从而提高其预报精度。在实际应用中，采用TLS-优化MGM(1,3)模型，获取更好的模拟和预报效果。

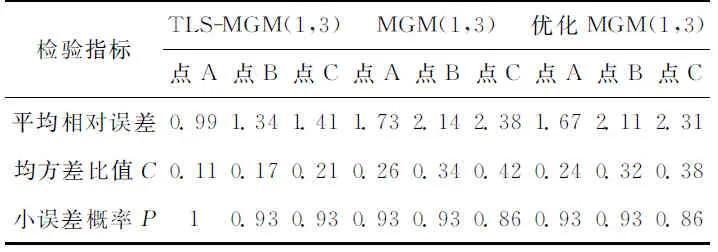
表3　多种评价指标的可靠性检验

4结论

MGM(1,n)模型综合不同监测点之间的相关信息，从整体上对多测点原始观测数据进行正确的处理，建立合理地预报模型，进而做出准确地预报，但传统MGM(1,n)模型的背景值构造限制了更精确的预报。本文通过分析传统MGM(1,n)模型误差产生的根本原因，引入TLS对其灰色模型参数矩阵修正，使得建模更加合理，从而有效地提高MGM(1,n)模型的预报精度。对于背景值优化的MGM(1,n)模型，克服因原始数据序列一阶累加生成序列非齐次指数函数而造成其预报精度不能改善的限制，使得MGM(1,n)模型更加稳健与可靠。因此，TLS-MGM(1,n)模型具有广泛的应用前景，同时，在实际应用中，也可先对背景值优化，然后再采用TLS解算灰色参数，进而提高其预报精度。

参考文献：

[1]赵志仁,徐锐.国内外大坝安全监测技术发展现状与展望[J].水电自动化与大坝监测,2010,34(5)：52-57.

[2]HU W S,ZHANG F,SONG L,et al.Study of Dam Deformation Model Based on Neural Network[J].Applied Mechanics and Materials,2012,170：2137-2142.

[3]沈细中,张文鸽,冯夏庭.大坝变形预测的 ANFIS 模型 [J].岩土力学,2006(增刊)：1119-1123.

[4]李守巨,刘迎曦,刘玉静.基于进化神经网络混凝土大坝变形预测[J].岩土力学,2004,24(4)：634-638.

[5]赵亮,兰孝奇,潘文琪,等.基于时间序列的大坝早期变形预测[J].水利与建筑工程学报,2012,10(3)：76-78.

[6]王利,张双成,李亚红.动态灰色预测模型在大坝变形监测及预报中的应用研究[J].西安科技大学学报,2005,25(3)：328-332.

[7]沈哲辉，黄腾，唐佑辉.灰色-马尔科夫模型在大坝内部变形预测中的应用[J].测绘工程，2015,24(2)：69-74.

[8]唐争气，谭志强.灰色时序组合模型在基坑监测中的运用[J].测绘工程，2014,23(2)：49-53.

[9]徐秀杰，黄张裕，刘国超，等.改进的灰色GM-AR组合模型在基坑监测数据处理中的应用[J].测绘与空间地理信息，2015，38(1):200-203.

[10]吴彦，张铎强，徐南.反向灰色模型的初值优化在道路沉降中应用[J].测绘工程，2014,23(12)：60-62.

[11]马符讯，徐南，马成.自适应变异粒子群优化灰色模型在变形分析中的应用[J].测绘工程，2014,23(5)：55-57.

[12]王新洲,范千,许承权,等.基于小波变换和支持向量机的大坝变形预测[J].武汉大学学报(信息科学版),2008,33(5)：469-471.

[13]李潇,徐进军.动态稳健支持向量机在大坝变形预测中的应用[J].大地测量与地球动力学,2009,29(2)：118-120.

[14]翟军,盛建明.MGM (1,n)灰色模型及应用[J].系统工程理论与实践,1997,17(5)：109-113.

[15]刘丹丹.灰色模型分析法在高层建筑物变形监测预测中的应用[J].测绘与空间地理信息，2014，37(2):203-205.

[16]程晨.灰色理论和多项式拟合在地表沉降监测中的应用[J].测绘与空间地理信息，2014，37(2):220-222.

[17]喜文飞，史正涛.基于卡尔曼滤波的动态灰色理论模型研究[J].测绘工程，2014,23(3)：24-27.

[18]何习平,华锡生,何秀凤.加权多点灰色模型在高边坡变形预测中的应用[J].岩土力学,2007,28(6)：1187-1191.

[19]崔立志,刘思峰,吴正朋.基于向量连分式理论的MGM (1,n)模型[J].系统工程,2009,26(10)：47-51.

[20]熊萍萍,党耀国,王正新.MGM (1,m)模型背景值的优化[J].控制与决策,2011,26(6)：806-810.

[21]刘寒冰,向一鸣,阮有兴.背景值优化的多变量灰色模型在路基沉降预测中的应用[J].岩土力学,2013,34(1)：173-181.

[22]陈义,陆珏,郑波.总体最小二乘方法在空间后方交会中的应用[J].武汉大学学报(信息科学版),2009,33(12)：1271-1274.

[23]鲁铁定.总体最小二乘平差理论及其在测绘数据处理中的应用[D].武汉:武汉大学,2010.

[24]陆珏,陈义,郑波.加权总体最小二乘方法在ITRF转换中的应用[J].大地测量与地球动力学,2011,(4)：84-89.

[责任编辑：李铭娜]

The multivariable grey model based on total least squares applicable for the dam deformation forecast

LU Chen-long1，2,KUANG Cui-lin1,CHEN Xiao-lin1,LU He-song1

(1.School of Geosciences and Info-Physics,Central South University,Changsha 410083,China;2.Zhengzhou City Municipal Engineering Design & Research Institute,Zhengzhou 450000,China;3.Zhongnan Engineering Corporation Ltd.,Co.,Changsha 410014,China)

Abstract：The background value error of traditional multivariable grey model MGM (1,n) will make the precision of grey parameters decline.The total least square is a kind of mathematical method which can simultaneously consider the observation error and model coefficient matrix error.Based on this,the MGM(1,n) model grey parameters are modified by introducing the total least square (TLS) method in this paper.Through the trial of a dam deformation data,the results show the proposed method can effectively improve the prediction accuracy.

Key words：dam deformation forecast；multivariable grey model；background value optimization；total least square

作者简介：卢辰龙(1987-)，男，硕士，助理工程师.

基金项目：国家973计划子课题(2013CB733303);湖南省国土资源厅科技项目(2012-41)

收稿日期：2014-09-30

中图分类号：TU196+.1

文献标识码：A

文章编号：1006-7949(2015)12-0048-05