比例射线移位算法的改进及其应用

刘　晴，郭庆胜，龙　毅

(1.武汉大学资源与环境科学学院，湖北武汉430079；2.南京师范大学地理科学学院，江苏南京210023)



比例射线移位算法的改进及其应用

刘晴1，郭庆胜1，龙毅2

(1.武汉大学资源与环境科学学院，湖北武汉430079；2.南京师范大学地理科学学院，江苏南京210023)

摘要：点状要素群移位的比例射线算法能够较好地保持移位后点群的空间分布模式。文中从农村居民地群移位的实际要求出发，对比例射线移位算法进行了改进：首先考虑居民地面积的不同大小对移位的影响；其次，设计比例射线移位的迭代方法；最后对于非常邻近的居民地群的移位，采用“微小”移位方法。通过实验验所改进的算法是有效的。

关键词：制图综合；点群移位；比例射线移位；农村居民地

移位算法,最初是为解决地图综合中比例尺缩放和符号化后引起的要素空间冲突而产生的算法，是制图综合的基本手段之一。随着地理空间数据比例尺的缩小，地图目标之间将不可避免地产生冲突[1]。制图综合中,对于地图要素间的空间冲突,主要是通过移位来解决,从而满足对象之间的最小间隔要求,并保持地图要素之间的邻近空间关系[2]。

地图上点状要素群的移位可简称为点群移位，有很多学者对点群移位进行过深入研究,提出了很多较为可行的移位算法[3-7]。但是点群自动移位在不同类别的点状要素群中会出现很多特殊情况，针对农村居民地群的空间特征，本文对比例射线移位算法进行了改进。

1比例射线移位算法简述

1.1　基本原理

比例射线移位是William A.Mackaness于1994年提出的，算法的主要思想是首先利用层次聚类算法确定潜在的空间冲突区域，找出产生空间冲突的对象群，将对象群看成一个整体，然后找到移位中心点[8]。冲突区域中每一个对象的移位距离都与其距离移位中心距离成函数关系，移位方向就是移位中心到每一个对象的射线方向。比例射线移位算法步骤如下：

1)设定一个合适阈值，通过基于最短距离的层次聚类算法将空间邻近点聚集为一个类群，确定要素间可能冲突区域；

2)确定每一个类群的移位中心点；

3)通过比例射线函数计算移位量，对群内点相对于中心点进行移位；

4)针对冲突区域边缘点移位量大的问题，通过引入衰减函数来控制局部变形和次生冲突。

1.2　算法的优势与不足

比例射线移位算法满足了诸多制图约束条件，在点群移位中，具有很强的优越性，主要包括以下优点：

1)实现了冲突的自动识别，计算量小，简单方便；

2)能够较好地保持要素间的空间关系，从而保证整体空间布局基本不变；

3)移位中心会自动向冲突最密集的位置靠近，从而能够保证大多数的点只移动一个最小距离。

原有的比例射线移位算法的不足之处主要包括：

1)没有考虑空间目标的大小，例如，建筑物有一定大小，不能仅仅简单地将它们看成同样的点；

2)无法确认能通过1次移位就解决所有空间冲突，在进行移位时，1次移位有时可能无法解决整个冲突区域的空间冲突问题；

3)有些空间冲突仅仅使用比例射线算法进行移位很难解决，这时还需要与其它算法相结合。

2算法的改进

2.1　考虑点群中空间目标的大小

William A.Mackaness在介绍比例射线移位算法时也曾提到过给每一个点状要素按照重要性分别赋予一个层级的思想[8]。也就是说，在执行移位的过程中，冲突区域内每一个点的重要性或者说层级是不同的，在移位中希望能够保证重要的点，移动的距离越小。实现这种思想的方法则是在确定移位中心时根据层级给每一个点赋予一个权重，对冲突区域内每一个点进行加权平均来确定移位中心。

比例射线移位算法是根据冲突区域内每一个点距离移位中心的距离，依照一定比率计算相应的移位量，然后对所有点进行射线式移位的算法。考虑建筑物的面积大小，移位中心的计算见式(1)：

(1)

求得移位中心后，冲突区域中每个点的移位量EDis与其距移位中心的距离Dis的关系见式(2)。

EDis=k×Dis×a×e-bx.

(2)

其中，k是移位比率，按照式(3)计算。

k=minLength/MinDis.

(3)

式(3)中，minLength是在保持清晰度的前提下地图上要素之间的最小间隔，一般为0.2 mm。MinDis是地图上该点群中距离移位中心最近点的距离值。

式(2)中a×e-bx是衰减函数模型[9]，x的计算见式(4)。

x=(Dis-MinDis)/(MaxDis-MinDis).

T：But something is wrong.What’s wrong?T：What is the size?

(4)

其中，Dis是当前点与移位中心的欧氏距离值，MaxDis是点群中距离移位中心最远点的距离值。

2.2　迭代过程

使用比例射线移位算法对冲突区域进行移位之后，一般情况下，点群空间冲突都基本能够得以解决，但是可能出现部分区域内依然存在着小范围空间冲突的情况。这个时候，如果改变移位函数的参数，冲突可能依旧难以解决或是容易造成其他要素的移位量过大。因此，本文设计了一个多次迭代的过程。其基本思想是：对冲突区域进行比例射线移位之后，再一次判断冲突，若仍然存在小部分冲突，则把依旧存在冲突的点群作为一个新的冲突区域，继续进行比例射线移位；如此循环下去，直到类似的空间冲突得以解决。

2.3　非常邻近居民地的移位

当冲突区域中两个或多个建筑物在空间上非常邻近，尤其是在其与移位中心的距离较远时，仅仅使用比例射线算法进行移位很难解决冲突。为此，本文提出了一种改进算法和Dewdney的“unhappiness”算法[10][11]相结合。这个算法的基本思想是：对于每一个对象，都在它当前位置的周围找几个可以替代它的位置，然后从中选择与周围对象的重叠度达到最小值那个位置，并将此位置作为该对象的新位置。

本文简化了Dewdney的“unhappiness”算法，先选取一个合适的生成候选点半径，对相应的点进行微小移动，然后继续利用改进的比例射线移位算法，对它们进行移位。过程如下：

1)选取非常邻近的农村居民地点群，计算中心点，并设置移位半径r；

2)在以中心点为圆心，r为半径的圆周上找到候选的8个新位置(分别为中心点圆周上从正北方向起，每隔45°确定一个新位置，组成这8个位置)；

3)在这8个候选的新位置中找到一个作为过于邻近要素的新位置；

4)对拥有新位置的点和整个冲突区域的其它点一起进行比例射线移位，并对结果进行评估，判断冲突的解决效果。

3算法的实验

为了验证改进后的比例射线移位算法，本文实验数据是法国一处农村居民地地图，来源于French national mapping agency Institute Geographic National，地图比例尺为1∶10 000，地图投影为Gauss_Kruger，坐标系是GCS_Beijing_1954。利用AE+C#编程实现该算法，软件的界面见图1。

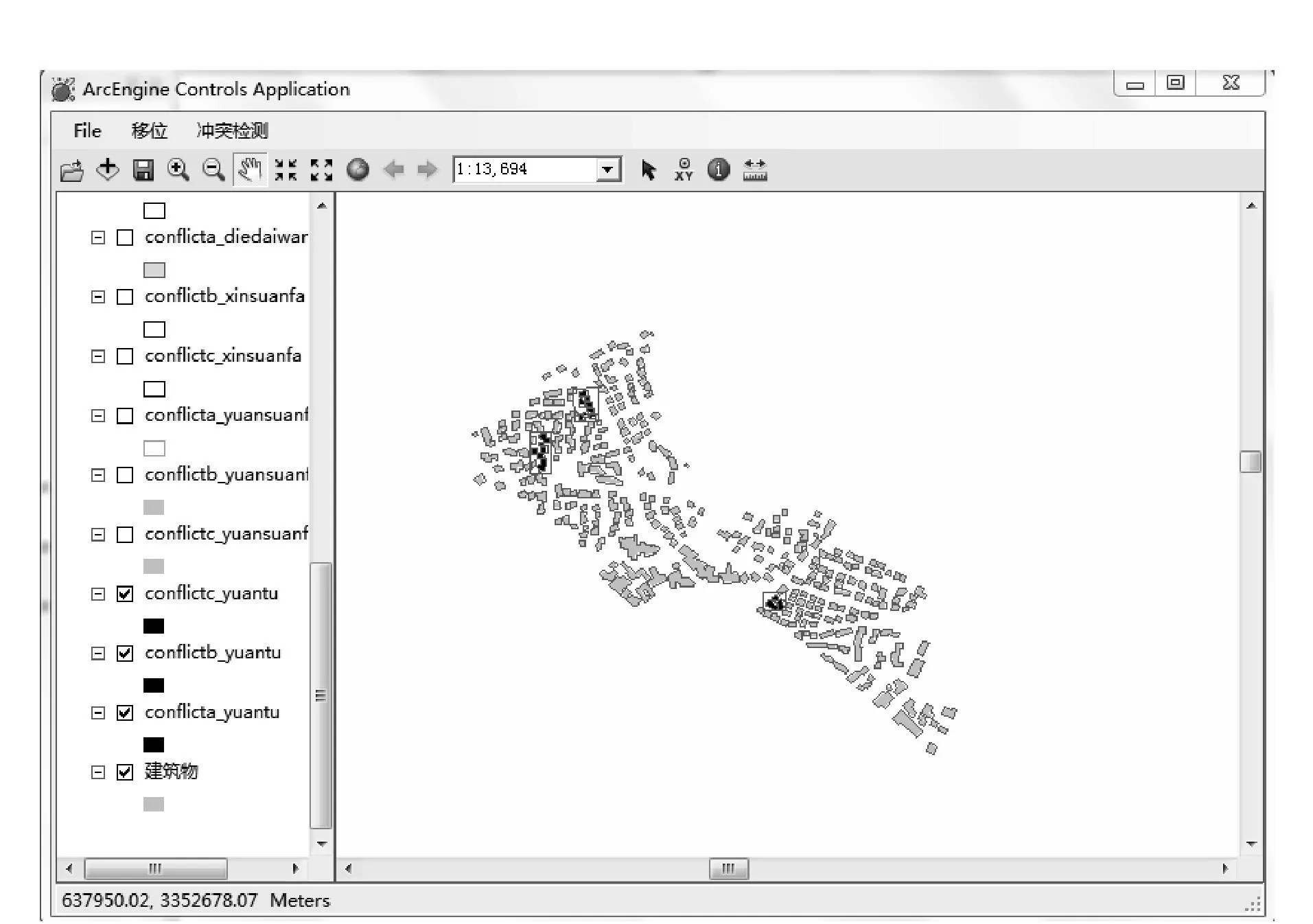
图1　软件界面

为了更好地说明算法的实验效果，在地图中找到三处典型的冲突区域，如图2所示。

图2　冲突区域

考虑建筑物面积大小后的移位结果见图3(本次实验中a=1,b=1)，图中灰色区域为建筑物原始位置，内边框为移位后的建筑物，外边框为冲突检测的缓冲区边界。可以看到冲突基本得以解决了。但是从图3中可以看到，图3(a)和图3(b)中还是存在冲突(见圆圈所示之处)，图3(b)中是新产生的冲突。很明显，这些冲突需要采用本文提到的迭代处理方法，图4及图5分别是对图3(a)和图3(b)进行迭代的结果。结果表明在进行比例射线移位迭代之后，空间冲突问题都得到了很好的解决。

图3　考虑面积大小的移位结果

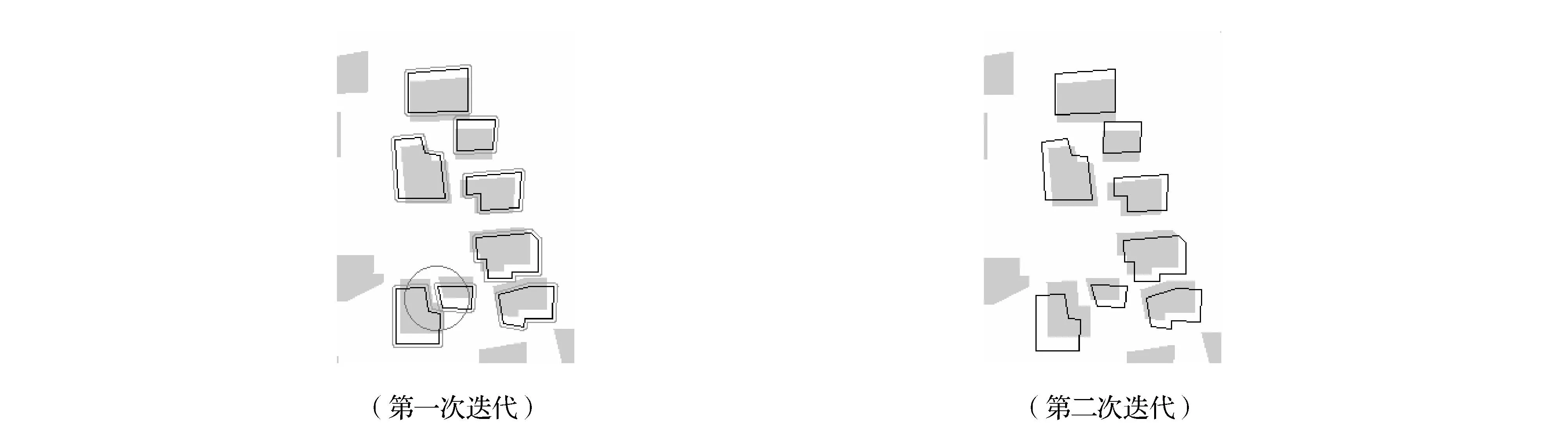
图4　冲突区域图3(a)的迭代过程

图5　冲突区域图3(b)的迭代过程

另外，图6是两个建筑物非常邻近且又距移位中心较远的情况，按照本文的方法进行了“微小”移位处理，新位置的选择见图6。

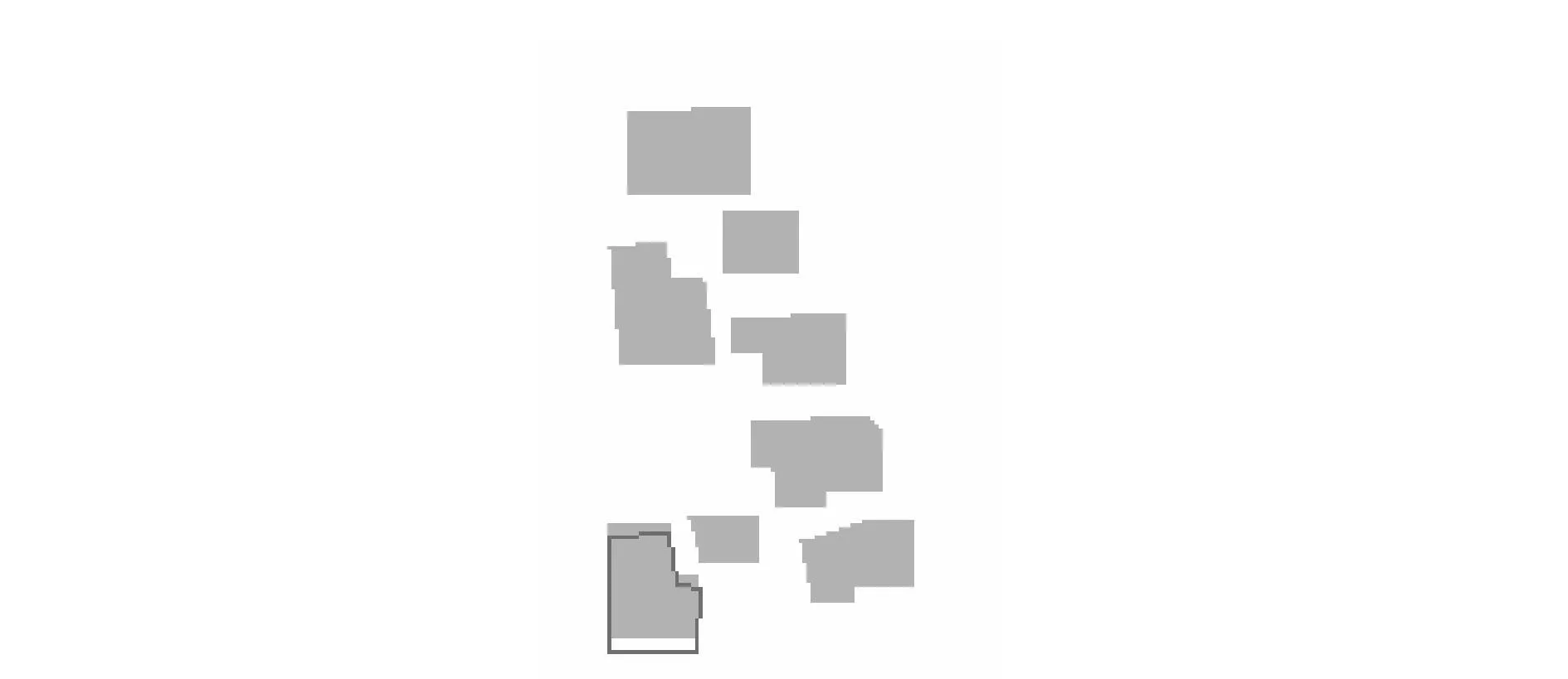
图6　新位置的选择

4结论与讨论

本文在点群移位已有的比例射线移位算法基础上提出了几点改进，并用AE+C#编程实现了该算法，取得了很好的实验结果，得到了以下的结论：

1)针对农村居民地移位的实际要求，考虑居民地面积的大小后，能够保证面积越大的建筑物移位的距离越小；

2)多次迭代的过程能够很好地解决新产生的类似空间冲突；

3)对于冲突区域中非常邻近且与移位中心距离较远的建筑物的移位，采用“微小”移位方法，即先进行微移位处理，再对整体采用比例射线移位算法进行移位，能够取得更好的效果。

农村建筑物群与道路等有密切关系，为了能解决不同要素之间的空间冲突，还需要进一步研究不同移位算法的结合。

参考文献：

[1]陈科,谢明霞,李柱林.基于面积分界尺度的居民地轮廓化简[J].测绘工程,2012,21(2):32-34.

[2]吴小芳,杜清运,胡月明,等.制图综合中移位算法概述分析[J].测绘科学,2008,33(2):117-120.

[3]艾廷华.基于场论分析的建筑物群的移位[J].测绘学报,2004,33(1):89-94.

[4]熊枝艳，刘远刚，郭庆胜，等.一种改进的点群移位算法及其应用[J].测绘与空间地理信息,2014,37(10):71-74.

[5]费立凡.用计算机模拟人类制图员解决地图缩编中的图形冲突[J].武汉大学学报(信息科学版),2004,29(5):426-432.

[6]侯璇,武芳,刘芳,等.基于弹性力学思想的居民地点群目标位移模型[J].测绘科学,2005,30(2):44-47.

[7]吴小芳,杜清运,徐智勇.多层次移位原则的道路与建筑物空间冲突处理[J].测绘学报,2010,39(6)：649-654.

[8]WILLIAM A.M.An Algorithm for Conflict Identification and Feature Displacement in Automated Map Generalization[J].Cartography and Geographic Information Systems,1994,21 (4):219-232.

[9]王成金.中国交通流的衰减函数模拟及特征[J].地理科学进展，2009，28 (5):690-696.

[10]WILLIAM A.M.Automated Displacement for Large Numbers Of Discrete Map Objects[J].Algorithmica,2001,30 (2):302-311.

[11]DEWDNEY A.K.Computer Recreations：Diverse personalities search for social equilibrium at a computer party[J].Scientific American,1987,257:112-116.

[责任编辑：王文福]

The improvement and application of proportional radial displacement

LIU Qing1,GUO Qing-sheng1,LONG Yi2

(1.School of Resource and Environment Science,Wuhan University,Wuhan 430079,China；2.School of Geographic Science,Nanjing Normal University,Nanjing 210023,China)

Abstract：The proportional radial displacement algorithm for the displacement of a group of points can be used to maintain spatial distribution patterns of points after displacement.In this paper,the proportional radial displacement algorithm is improved according to the real demand of rural residents’ displacement.Firstly,the size of rural residents is put into consideration during displacement;secondly,an iterative method of proportional radial displacement is designed;lastly,a “minimum” displacement method is proposed for rural residents which are too closed to each other.The effectiveness of the improved algorithm is verified by means of the practical test.

Key words：cartographic generalization；points displacement；proportional radial displacement；rural residents

作者简介：刘晴(1992-)，女，硕士.

基金项目：国家863计划资助项目(2012AA12A402 );国家自然科学基金资助项目(41071289，41171350，41471384)

收稿日期：2014-11-18

中图分类号：P283.1；TP319

文献标识码：A

文章编号：1006-7949(2015)12-0068-04