基于稀疏AR建模信号去噪研究与应用

第一作者宋欢欢女，硕士生，1989年4月生

通信作者叶庆卫男，副教授，1970年4月生

基于稀疏AR建模信号去噪研究与应用

宋欢欢，叶庆卫，王晓东，周宇

(宁波大学信息科学与工程学院， 浙江宁波315211)

摘要：为去掉在不同环境、设备下所采集信号中的不同分布形态噪声，引入稀疏优化求解思路构建新的去噪算法。设信号的AR模型系数是稀疏的，且噪声对AR模型系数影响均衡分布，则可用采集的含噪声信号构建稀疏AR模型有效消除噪声。用含噪声信号构建AR系数矩阵作为过完备稀疏基，通过多次重复随机抽取方式获得多个欠定方程组；利用稀疏优化求解算法获取AR模型稀疏系数；据稀疏系数平均值重构信号。仿真实验表明，信号含噪声较大时该算法较经典小波及中值滤波去噪效果更好。

关键词：多频信号；AR模型；稀疏表示；过完备稀疏基

收稿日期：2013-10-21修改稿收到日期：2014-04-03

中图分类号:TP391.4文献标志码：A

基金项目：国家科技支撑计划项目(2011BAF14B04);江苏省自然科学基金资助项目(BK2011504);江苏高校优势学科建设工程资助项目(PAPD);江苏省博士后基金资助项目(1201024B);国家博士后基金(2012M521008)

A new algorithm of signal de-noising based on sparse AR model

SONGHuan-huan,YEQing-wei,WANGXiao-dong,ZHOUYu(Information Science and Engineering College, Ningbo University, Ningbo 315211, China)

Abstract:A actual signal always contains noise due to different surroundings and collecting devices. And the noise has different forms. A signal de-noise algorithm is an important pre-processing tool. Here, a new de-noise algorithm was proposed based on sparse optimization. It was assumed that coefficients of signal’s AR model are sparse and the noise effect on coefficients of AR model has an even distribution. A sparse AR model was built for the signal with noise. The AR coefficient matrix was constructed with the noised signal, and the matrix was taken as the over-completed sparse basis. Several underdetermined equation sets were obtained by extracting randomly some rows several times from the over-completed sparse basis. Then, the sparse AR coefficients were solved with the sparse optimization algorithm. At last, the AR coefficients were averaged, and the de-noised signal was reconstructed with the averaged AR coefficients. The simulation results showed that the de-noising effect obtained with the proposed algorithm is better than those of the classical wavelet de-noising algorithm and the median filtering de-noising algorithm.

Key words:multi-frequency signal; AR model; sparse representation; over-completed sparse base

在实际实验中信号分析只能针对采集的信号进行研究。由于外界环境、检测设备不完善造成所采信号含噪声干扰，有用信息被噪声淹没，无法对信号准确分析研究，故须先对信号进行去噪预处理。小波去噪为常用的多频信号去噪方法。基于小波变换的信号去噪算法有诸多阈值方法，如文献[2]对阈值方法缺陷进行阐述：在信号不连续区域会出现Gibbs现象；信噪比较大时去噪效果明显下降；逐点处理小波系数时忽视其完整性；阈值选择较关键，据信号不同，信噪比不同，阈值选择随之改变，阈值选择不好会影响去噪效果，从而增加小波去噪实际操作难度。文献[3-5]对小波去噪算法进行改进，提出的新小波阈值算法包含传统硬、软阈值方法优点；并据传统小波阈值算法将信号噪声值域中的小波系数差别及权重加大以便确定阈值，取得更好的去噪效果，但小波算法的Gibbs现象仍然存在；基于稀疏表示的小波去噪引入随机测量矩阵对小波系数进行变换，并考虑小波系数的整体性，但仍要求据实验经验选择合适阈值及好的测量矩阵。

多频信号中的噪声主要分为加性噪声与乘性噪声。加性噪声主要有脉冲噪声及白噪声，而乘性噪声会改变信号的振动幅值，较复杂。本文实验仿真主要对含白噪声的多频信号去噪。先用采集的带噪声信号构建自适应过完备稀疏基，随机抽取其m行构造矩阵，其中m小于过完备稀疏基列数；再对信号进行稀疏表示，因过完备稀疏基含信号的结构特征，而噪声信号无此特征，则噪声信号映射到过完备稀疏基的参数非常小，用l1算法计算可自动清除较小噪声参数；再用所求稀疏系数与过完备稀疏字典相乘获得去噪后信号。此时所得信号并非完整信号，其前部分并未得到去噪处理。本文实验仿真用双向稀疏去噪完成对整个信号的去噪。因需处理的信号符合AR模型，将信号倒置，所得新信号亦符合AR模型。据此，本文对倒置后所得信号去噪处理，与原始采集信号去噪所得信号合并进结果。本文定义此操作为双向稀疏去噪，通过与小波去噪、中值滤波去噪算法比较，证明该算法去噪效果较好。

1基于稀疏AR建模的信号去噪基本原理

1.1基于AR模型的过完备稀疏基构造

设信号符合AR模型，即

(1)

由式(1)看出，AR模型具有较强的时间相关性，即第k时刻信号xk只与其前p时刻信号xk-l(l=1,2,…,p)有关，与其它时刻信号、激励无关。第k时刻信号xk可以由前p个时刻信号线性表示。对某信号采样n点，因该信号符合AR模型，得方程组为

(2)

将式(2)写成矩阵形式，即

(3)

(4)

式中：Z定义为过完备稀疏基，且要求n-p>p。

1.2稀疏表示

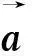
(5)

式中：i1，i2，…，im为行号。令

式(5)为欠定方程组，有无穷个解，而所需解为最稀疏解，则方程组可转换为

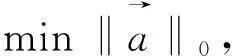
(6)

式中：ε为实数。

(7)

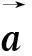
1.3重构去噪

(8)

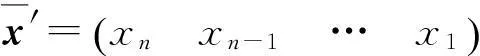
(9)

图1为基于稀疏AR建模信号去噪算法流程图及算法具体步骤。

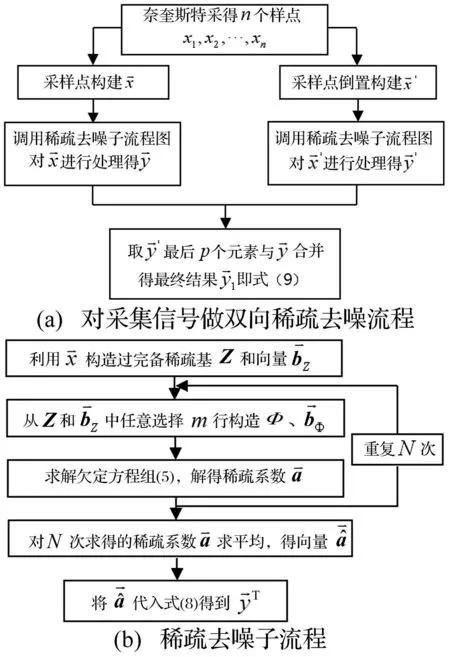
图1　基于稀疏AR建模信号去噪算法流程图 Fig.1 The flow chart ofsignal de-noising algorithm based on sparse AR model

2实验仿真

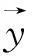
原始信噪比为

(10)

复原后信噪比为

(11)

小波去噪复原后信噪比为

(12)

中值滤波去噪复原后信噪比为

(13)

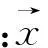
仿真采用ϑ1内点法求解稀疏系数，其中参数λ=0.1，精度为0.001。设仿真信号为多频信号，即

x0(t)=sin(200πt+0.1)+3cos(260πt+0.9)+

0.7sin(340πt+1.5)+1.2cos(140πt)

(13)

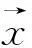
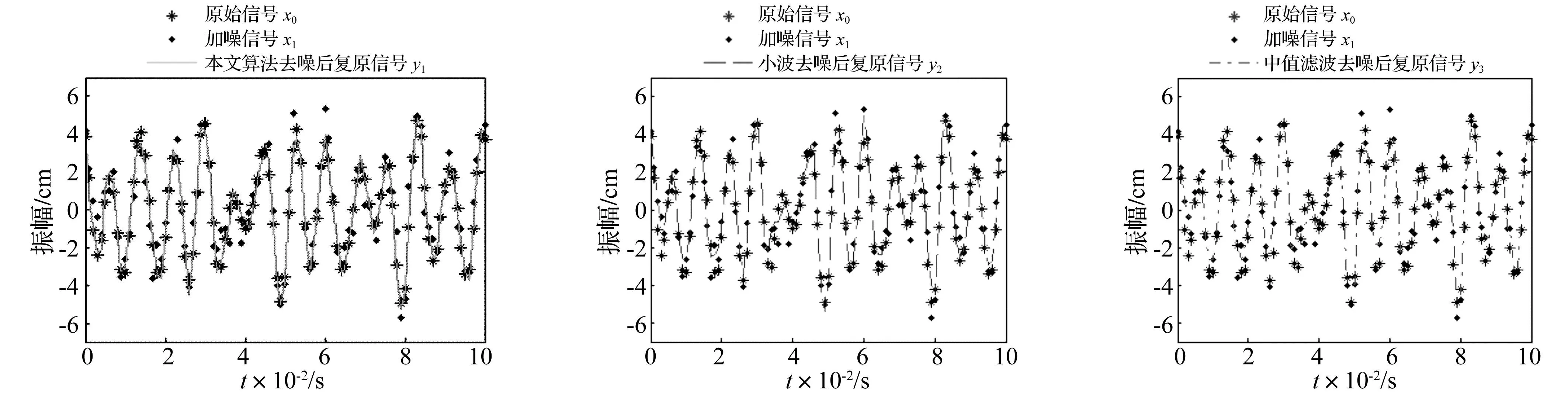
(a) SNR0=9.54dB,SNR1=18.89dB(b) SNR0=9.54dB,SNR2=12.86dB(c) SNR0=9.54dB,SNR3=10.47dB图2 不同算法去噪复原信号对比Fig.2Thechartofcomparesignalswhichrecoveryfromonesignalusingtwodifferentde-noisingalgorithms

图3　两种算法对不同信噪比的信号去噪比较图 Fig.3 Comparision chart of different SNR signal’s de-noising use two algorithms

3实际应用

用本文算法对实际采集的振动信号进行去噪。工程数据采自宁波某斜拉索大桥。大桥全长67m，由102根直径0.15m拉索构成支撑系统；用WS-ZHT2振动设备及双传感器采集振动信号。双传感器安装于拉索及梁端铰支处，以便能有效感应索-梁耦合的拉索振动，见图4。

图4　传感器安装图 Fig.4 The picture of sensor installation

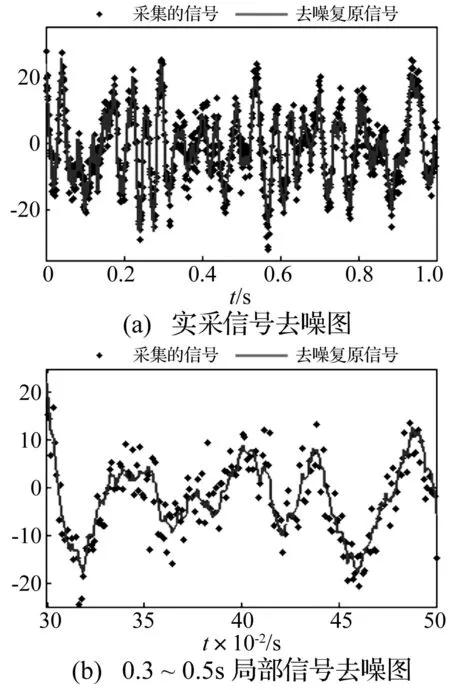
图4　本文算法对实采信号去噪前后对比 Fig.4 The figure of compare original signal to de-noising signal using the algorithm the paper proposed

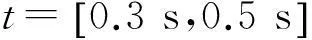
4结论

(2)本文算法基于信号自身的结构特点进行去噪处理，在实验仿真、实际应用中对带较大噪声符合AR模型信号的去噪效果均较好。参数L、m据采集的信号数据及经验人为设定，L、m值不同去噪效果不同。

(3)本文中过完备字典D由随机抽取完整字典矩阵Z的m行构成(m

参考文献

[1]Tsaig Y,Donoho D L.Extensions of compressed sensing[J]. Signal Processing,2006,86(3):549-571.

[2]Kelly S E. Gibbs phenomenon for wavelets[J].Applied Computational Harmonic Analysis,1996,3(1):72-81.

[3]唐进元,陈伟涛,陈思雨,等.一种新的小波阈值函数及其在震动信号去噪分析中的应用[J].振动与冲击,2009,28(7): 118-121.

TANG Jin-yuan,CHEN Wei-tao,CHEN Si-yu,et al.A new function of Wavelet threshold applied in Vibration signal denoising analysis[J].Journal of Vibration and Shock, 2009, 28(7):118-121.

[4]王宏强,尚春阳,高瑞鹏,等.基于小波系数变换的小波阈值去噪算法改进[J].振动与冲击,2011,30(10):165-168.

WANG Hong-qiang,SHANG Chun-yang,GAO Rui-peng, et al.An improvement of wavelet shrinkage denoising via wavelet coefficient transformation[J].Journal of Vibration and Shock,2011,30(10):165-168.

[5]赵瑞珍,刘晓宇,LI Ching Chuang,等.基于稀疏表示的小波去噪[J].中国科学,2010,40(1):33-40.

ZHAO Rui-zhen,LIU Xiao-yu,LI Ching Chuang,et al.Wavelet denoising based on sparse representation[J].Chinese Science, 2010,40(1):33-40.

[6]Candes E J.The restricted isometry property and its implications for compressed sensing[J].Comptes Rendus Mathematique,2008,346(9/10):589-592.

[7]Donoho D.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.

[8]Tsaig Y, Donoho D L.Breakdown of equivalence between the minimal l1-norm solution and the sparsest solution[J]. Signal Processing,2006,86(3):533-548.

[9]Kim S J, Koh K, Lustig M, et al.An Interior-point method for large-scale l1-regularized least squares[J].IEEE Journal of Selected Topics in Signal Processing,2007,4(1):606-617.

[10]张春梅,尹忠科,肖明霞.基于冗余字典的信号超完备表示与稀疏分解[J].科学通报,2006,51(6):628-633.

ZHANG Chun-mei,YIN Zhong-ke,XIAO Ming-xia. Overcompleted expression and sparse decomposition of signal based on redundant dictionary[J].Journal of Chinese Science Bulletin,2006,51(6):628-633.

[11]叶庆卫，王同庆.基于幅谱分割的粒子群最优模态分解研究与应用[J].仪器仪表学报,2009,30(8):1584-1590.

YE Qing-wei,WANG Tong-qing.Optimization modal analysis with PSO based on spectrum segmentation[J].Chinese Journal of Scientific Instrument,2009,30(8):1584-1590.

[12]Ye Qing-wei,Sun Yang,Wang Xiao-dong,et al.An improve LLE algorithm with sparse constraint[J]. Journal of Computational and Theoretical Nanoscience, 2013, 12(10): 2872-2876.

[13]刘洪江.稀疏信号重构[J].计算机与现代化,2010,10:142-146.

LIU Hong-jiang.Reconstruction of sparse signal[J].Journal of Computer and Modern,2010,10:142-146.

[14]阳子婧,蔡力钢,高立新.自适应冗余提升小波降噪分析及其在轴承故障识别中的应用[J].振动与冲击,2013,32(7):54-57.

YANG Zi-jing,CAI Li-gang,GAO Li-xin.Adaptive redundant lifting wavelet denoising analysis and its application in bearing fault identification[J].Journal of Vibration and Shock,2013,32(7):54-57.

[15]叶庆卫,袁德彬,王晓东,等.斜拉索非线性振动信号粒子滤波分析与应用[J].振动与冲击, 2013, 32(5):108-112.

YE Qing-wei,YUAN De-bin,WANG Xiao-dong, et al. Analysis of non-linear vibration signal of inclined cables based on particle filter[J]. Journal of Vibration and Shock, 2013, 32(5):108-112.