基于TOPSIS多目标遗传优化的面板数据综合评价



基于TOPSIS多目标遗传优化的面板数据综合评价

李荣富1，傅懿兵2，王萍3

(1.池州学院经贸系，安徽池州247000；2.烟台职业学院会计系,山东烟台264000；3.东北财经大学经济学院，辽宁大连116025)

[摘要]针对面板数据综合评价中多评价对象、多指标、多时间段的特点，以TOPSIS与多目标优化遗传算法集成的思路将综合评价问题转化为多目标优化问题，考虑多指标权重和时间权重因素，运用遗传算法实现多目标优化得到多个评价对象最优接近度的帕累托前沿，实例仿真结果表明对数据的综合信息利用比较充分。

[关键词]面板数据；多目标优化；动态综合评价；非劣解；帕累托前沿

1　引言

面板数据是多指标综合评价实践中常见的却又难以处理的一种数据类型，其数据结构表现为时间、空间（区域、对象或方案）和指标三个维度，具有动态多指标（属性）的复杂特征。根据面板数据所做的综合评价属于动态综合评价，在工程、经济、管理、教育、信息、科技等领域得到广泛应用。例如，对多个区域或国家的经济增长质量、经济竞争力、综合实力、科技竞争能力等方面通过构建指标体系同时进行时间维度、空间维度的综合评价；某一系统内各个单位在某历史阶段的经济管理绩效的综合对比；不同时间、多个方案在多维指标测度水平上的筛选问题，等等。面板数据的综合评价不同于二个维度的单指标综合评价、静态的多指标综合评价[1-4]，以及同一空间的动态多指标综合评价[5]，它既需要同时考虑时间、空间的权重因素，又要解决多指标的评价模型问题。研究面板数据的评价问题有利于充分利用有限的数据信息，更好地反映决策空间的整体动态变化过程，对帮助科学化的定量决策有着非常重要的现实价值。有影响的面板数据综合评价研究成果可以分为二大类：一类是以TOPSIS（Technique for Order Preference by Similarity to Ideal Solution，逼近理想点排序法）[6]为基础展开的、侧重于综合评价模型的应用研究。樊治平和肖四汉（1993）是较早涉入此类问题的学者,他们根据TOPSIS原理纳入时间和指标权重因素，建立起各决策方案（或空间）对理想解的相对接近度作为综合评价模型（函数），即所谓“理想矩阵法”[7]，以最大化的相对接近度作为决策依据。在这一研究基础上，樊治平和肖四汉（1995）将TOPSIS与灰色系统理论中的关联分析法相结合，通过计算理想矩阵元素与规范化决策矩阵元素的关联系数，利用时间权重和指标权重对前者进行线性加权求和而得到每个方案与理想方案和负理想方案的关联度（接近度）[8]。针对动态多指标综合评价中的指标赋权，樊治平和王欣荣（2000）根据多指标的不同类型，考虑指标的优劣程度和增长程度，分别计算每个决策方案的综合评价值，然后运用加权法则建立优化模型得到最终的方案排序结果[9]，但指标好坏程度和增长程度两种情况相对重要程度的确定具有主观性。李素兰,吕旭彬（2008）也作了类似的应用研究，分析了2001－2004年浙江省各城市发展的动态[10]。金菊良、汪淑娟和魏一鸣（2004）在“理想矩阵法”基础上运用投影寻踪(Projection Pursuit)原理，将决策方案的相对接近度转化成以时间和指标为决策变量的投影寻踪目标函数，通过实数加速遗传算法(Real Coding Based Accelerating Genetic Algorithm)优化得到时间和指标权重矢量，以最大化的投影函数值（综合评价值）作为方案排序依据[11]。李浩宾（2009）沿用这一方法对泛珠江三角洲区域科技资源配置效率进行了应用性的分析和评价[12]。另一类是从面板数据自身结构特征出发，反映决策方案的整体差异，侧重于多指标权重的客观性赋权研究。郭亚军（2002）提出“纵横向拉开档次”法，以最大可能地体现出各被评价对象之间的差异为指标权重的取值原则，证明当指标权重取对称矩阵的最大特征值所对应的特征向量时，总离差平方和达到最大值，而总离差平方和可以较好地体现决策方案在数据（时序立体数据）上的整体性差异，然后通过客观赋权的多指标权重对规范化的指标数据进行线性加权求和而得到决策方案的动态综合评价值[13]。这种方法实质上是将面板数据由三维降为二维（时间、指标），即反映的是同一空间的动态多属性综合评价，而没有体现决策空间的综合信息，并且对称矩阵要求为正矩阵。为弥补这一缺陷，郭亚军,胡蕾,王志刚（2011）提出“三次差异驱动”的动态综合评价思路，既分别考虑多指标、时间因素的作用，又将各决策方案动态综合评价值的差异性（能量消耗）突显出来[14]，但权重的确定需要经验知识。通过比较二大类面板数据综合评价的研究成果，本文将以实用、易于理解掌握和评价结果的客观性为宗旨，吸收第一类研究成果的基本评价方法（如TOPSIS、遗传优化方法），借鉴第二类研究成果对数据总体差异性的研究思路，避免其计算综合评价值稍显繁杂和对数据利用的客观限制，采用TOPSIS与多目标优化遗传算法集成的途径同时实现各决策空间对理想解的最大化相对接近度、指标权重和时间权重，并应用实例进行佐证。

2　面板数据结构描述

设有q个评价方案Sl(l=1,2,…,q)，每个Sl有n个评价指标Pj(j=1,2,…,n)，则xijl(i=1,2,…m,j=1,2…n)表示某方案l在i(i=1,2,…m)时间的第j个指标的观测值。其数据结构也可以用表格直观显示（见表1）。

3　TOPSIS多目标遗传优化步骤

运用TOPSIS多目标遗传优化进行面板数据综合评价的基本思想是，建立具有时间、指标和方案的逼近于理想解的相对接近度作为各决策方案的非线性目标函数，由于以各方案最小化的对理想解的相对接近度作为决策排序依据，因而综合评价实际上转化为多目标优化问题，运用遗传算法求解所得各方案的最优接近度即为综合评价值，时间、指标的值为决策变量的非劣解。具体建模步骤如下：

表1　面板数据的一般结构

步骤1：观测值的同趋势化[15]。同趋势化后，方案l的数据矩阵表示为：，面板数据矩阵表示为：。

步骤2：同趋势化数据的规范化处理。为了消除数据间量纲差异，对同趋势化后的数据进行规范化，此处采用文献[7]的处理方法。也可以依据文献[15]提出的简易“均值化”处理方法。

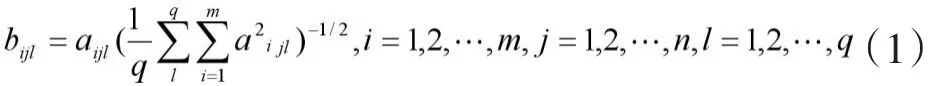
步骤3：产生理想矩阵和负理想矩阵。借鉴文献[7]，由规范化矩阵B分别产生理想矩阵和负理想矩阵，其中

。

步骤4：建立非线性多目标模型。以各方案对理想解的相对接近度作为目标函数，将规范化矩阵B、理想矩阵B+和负理想矩阵B-综合成以时间和指标权重为决策变量的非线性多目标优化模型。

步骤5：优化求解。根据（2）编制多目标优化程序，运用遗传算法（Genetic Algorithm）的鲁棒性、并行处理和全局寻优的特点[16]求解各方案对理想解的最优接近度、时间权重λj(j=1,2,…,m)和指标权重wj(j=1,2,…,n)的解集。

步骤6：实现综合评价。由于非线性多目标优化问题的复杂性，采用遗传算法寻找的是作为适应度函数的多目标函数问题的局部非劣解集和相应的多目标函数值集而不是最优解和最优多目标值，这就需要根据帕累托前沿的多目标函数值集、决策变量解集进行分类统计排序。将优化求解的各方案对理想解的最优接近度z(1),…,z(l),…,z(q)取绝对值后按大小进行排序，以众数的排序结果作为方案的决策比较依据，结合时间、指标权重对各方案进行分析和对比。

4　实例仿真

以文献[7]的辽宁省5个城市独立核算工业企业经济效益的5个指标数据为例（见表2）。5个城市视为5个决策方案，分别以A－E表示；5个指标分别以x1-x5表示，均为成长型指标；1988－1990年为3个时间段。

表2　1988－1990年5个城市独立核算工业企业经济效益

按照步骤1－3得到理想矩阵和负理想矩阵；由步骤4－5，在美国MathWorks公司的MATLAB软件环境下以各方案对理想解的相对接近度取负值（因为gamultiobj实现的是多目标最小化）作为适应度函数编制程序（*.m文件）即句柄函数，决策变量个数为8（＝指标数5+时间段3），以指标权重和时间权重的线性、非零为约束条件，调用多目标遗传算法（Multiobjective Genetic Algorithm）工具箱中的gamultiobj函数。本例对该函数中的其他参数（如种群、选择、变异、交叉和迁移等）采用默认设置，其中种群规模默认为决策变量个数的15倍。本例经过102步迭代后得到取绝对值的最优帕累托前沿（适应度函数值和决策变量）35%（ParetoFraction）的解集，各有42个（＝15×8×35%）基因组，见表3和表4。

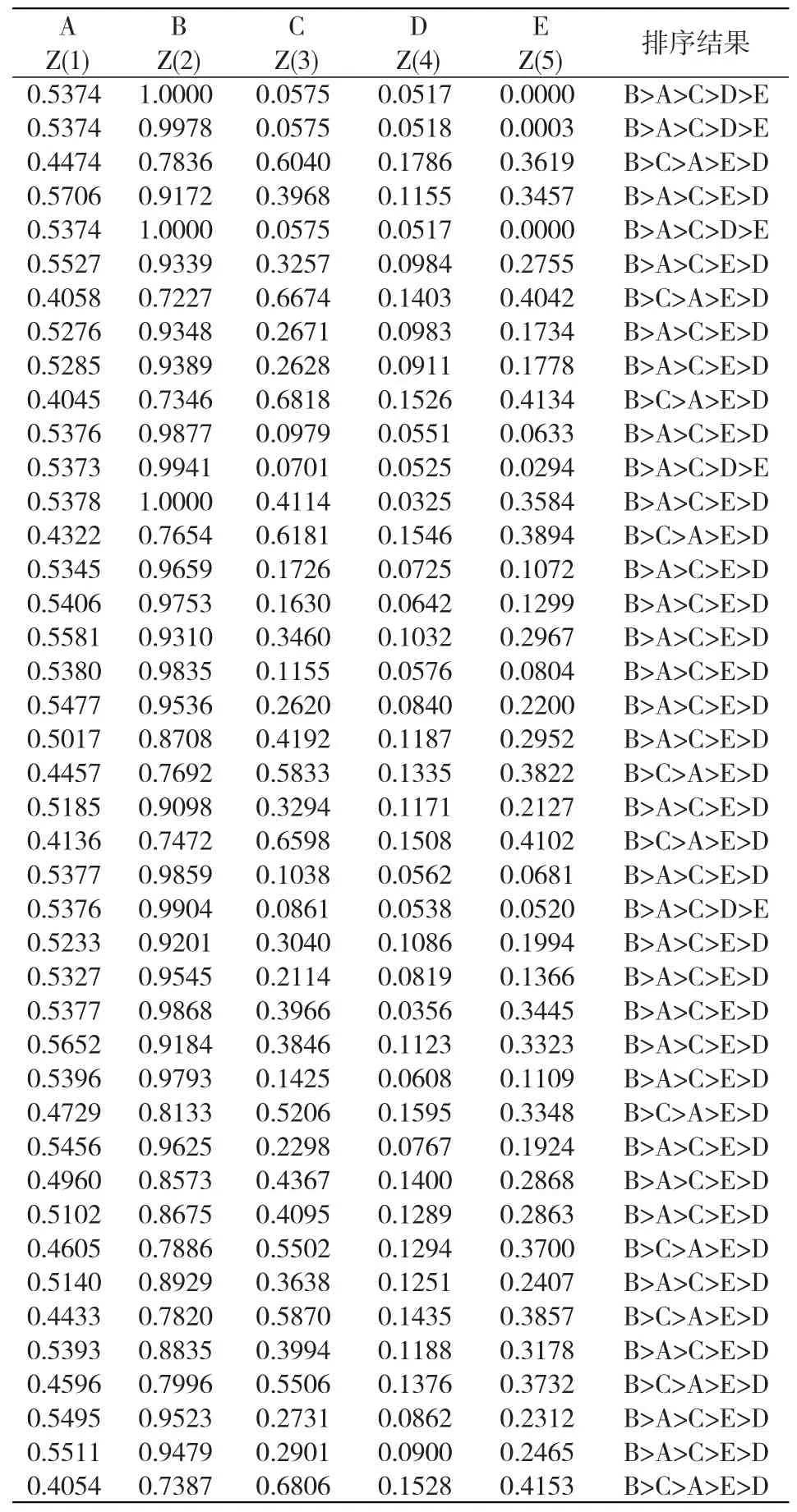
表3　5个决策方案的适应度值集

由步骤6，将步骤5的帕累托前沿的适应度函数值集按大小排序（结果见表3），B>A>C>E>D为26次，B>A>C>D>E为5次，而B>C>A>E>D出现11次。因此，取出现次数最多的B>A>C>E>D作为本例5个决策方案的排序结果，即5个城市独立核算工业企业经济效益的综合评价参考顺序，这个结果与文献[7]取指标的相等权重1/5、时间的相等权重1/3得到的评价结果B>C>A>E>D接近，表现在A和C的顺序不同，这也是综合评价实践中的正常现象，“…因为不同的评价方法本身有着不同的特点，体现着评价者不同的思想和导向，其结果有所不同，甚至差异较大，这才是正常的”[17]。对应于B>A>C>E>D排序的非劣解集中的权重值，指标权重主要表现为w2＞w3＞w4＞w5＞w1,时间权重为λ1＞λ3＞λ2。在评价分析时，还可以参照B>A>C>D>E和B>C>A>E> D，分析A和C、E和D的排序差异，结合权重的不同找出原因以利于帮助企业改进经营管理。

表4　决策变量（指标和时间权重）的非劣解集

5　结语

本文探讨的TOPSIS与多目标遗传优化集成的面板数据综合评价方法继承了TOPSIS的几何意义明显的优点，既考虑了多指标权重和时间权重的影响，又可以通过遗传算法实现多目标优化得到多个评价对象最优接近度的帕累托前沿；计算复杂度比较低，多目标优化程序可以直接利用MATLAB软件中的多目标遗传算法工具，减少研制遗传算法程序的工作量；实例仿真表明这种方法比较好地利用了面板数据的综合信息。由于面板数据综合评价的复杂性，某一种方法只能近似地反映评价对象的真实综合状况，因而还需要配合定性的分析，在综合评价实践中不断地接受检验和完善。

参考文献：

[1]何平,倪苹.中国城镇化质量研究[J].统计研究,2013,30(6):11-18.

[2]杨洁.基于PDCA循环的内部控制有效性综合评价[J].会计研究,2011(4):82-87.

[3]齐敏芳,付忠广,景源,等.基于信息熵与主成分分析的火电机组综合评价方法[J].中国电机工程学报,2013,33(2):58-64.

[4]郭亚军,马凤妹,董庆兴.无量纲化方法对拉开档次法的影响分析[J].管理科学学报,2011,14(5):19-28.

[5]张鹏侠，韩静华，姜沈利.灰色多层次综合评判模型在评价经济效益中的作用[J].沈阳航空工业学院学报,1994(9):81-87.

[6]H.Wang.C. L, Yoon.K. S. Multiple attribute decisionmaking[M]. Berlin:Spring-Verlag, 1981.

[7]樊治平,肖四汉.有时序多指标决策的理想矩阵法[J].系统工程,1993,11(1):61-65.

[8]樊治平,肖四汉.一类动态多指标决策问题的关联分析法[J].系统工程,1995,13(1):23-27.

[9]樊治平,王欣荣.时序多指标决策的一种新方法[J].预测,2000 (4):49-50，45.

[10]李素兰,吕旭彬.城市发展的动态综合评价[J].统计与决策, 2008(4):104-105.

[11]金菊良，汪淑娟，魏一鸣.动态多指标决策问题的投影寻踪模型[J].中国管理科学，2004，12（1）：64－67.

[12]李浩宾.泛珠江三角洲区域科技资源配置效率综合评价-基于遗传投影寻踪方法[J].科技进步与对策,2009,26(6):133-138.

[13]郭亚军.一种新的动态综合评价方法[J].管理科学学报, 2002,5(2):49-55.

[14]郭亚军,胡蕾,王志刚.具有三次差异驱动特征的动态综合评价方法[J].系统工程学报,2011,26(4):546-550.

[15]叶宗裕.关于多指标综合评价中指标正向化和无量纲化方法的选择[J].浙江统计，2003（4）：24-25.

[16]雷英杰，张善文，李续武.MATLAB遗传算法工具箱及应用[M].西安：西安电子科技大学出版社，2011.

[17]胡永宏.对统计综合评价中几个问题的认识与探讨[J].统计研究,2012,29(1):26-30.

[责任编辑：余义兵]

作者简介：李荣富（1966-），男，安徽怀宁人，池州学院经贸系副教授，硕士，研究方向为经济增长，国际贸易与计量经济；傅懿兵（1969-），女,山东烟台人，烟台职业学院会计系讲师，硕士，研究方向为劳动经济学；王萍（1962-），女，辽宁大连人，东北财经大学经济学院教授，博士，研究方向为劳动经济学，人力资源开发与管理。

基金项目：安徽省教育厅人文社会科学研究重点项目（SK2013A123）。

收稿日期：2014-12-28

DOI:10.13420/j.cnki.jczu.2015.02.012

[文章编号]1674-1102(2015)02-0046-04

[文献标识码]A

[中图分类号]F202