顾及测区地形的水准网定权新方法研究

2016-01-05张鑫,刘成龙,龚率等

测绘工程 2015年4期

顾及测区地形的水准网定权新方法研究

张鑫1，刘成龙1，龚率2，宋韬1，聂虎啸1

(1.西南交通大学地球科学与环境工程学院，四川成都610031;2.成都市勘察测绘研究院，四川成都610081)

摘要：针对目前水准网平差中高差定权方法未能较好地考虑地形环境对高差观测误差的影响关系的问题，提出一种顾及测区地形起伏并根据测段往返测高差较差的水准网高差分类定权新方法。理论分析和实际数据证明，在水准网中既有地形起伏较大的测段，又有地形起伏不大的平缓测段时，采用文中提出的定权方法比传统定权方法更能真实反映水准网测量的精度情况，弥补了传统定权方法的不足。

关键词：水准网平差；往返测高差较差；定权；方差一致性检验；地形因子

中图分类号：P207文献标志码：A

收稿日期：2014-02-19

作者简介：张鑫(1989-)，男，硕士研究生.

Anewstudyofweightingmethodinlevelingnetworkadjustmentconsideringtheterrain

ZHANGXin1，LIU Cheng-long1，GONG Shuai2，SONG Tao1，NIE Hu-xiao1(1.SchoolofGeoscienceandEnvironmentEngineering，SouthwestJiaotongUniversity，Chengdu611756，China；2.ChengduInstituteofSurveyingandInvestigation，Chengdu610081，China)

Abstract：Aiming at the problem of failing to take the terrain condition affecting the method of height difference weighting into account，it proposes a new leveling network weighting method which takes the terrain condition in the survey area into account.Proved with theoretical analysis and practical data，in the leveling network with both large and small topographic reliefs，test results show that the method has better performance in reflecting the precision of leveling than traditional methods of weight，and covering the deficiency of the traditional one.

Keywords：levelingnetworkadjustment；discrepancyfordirect-reverseobservation；weighting；testforuniformvariance；terrainfactor

目前，几何水准测量仍然是获取高精度高程的唯一方法[1]。随着现代测量数据处理技术的不断发展进步[2]，水准测量的精度得到了很大程度的提高，水准网数据处理方法也相应地有所改变。通常情况下是利用间接平差的方法对水准网进行数据处理，其中在高差定权方式的选择上，一般遵循如下准则：在地形起伏不太显著的区域，按测段的水准路线长度定权[3]；在地形起伏较为显著的区域，按测段的测站数定权。但在地形复杂的区域因同时存在各种不同起伏状况的测段，故单独使用距离定权或测站数定权均不能准确反映水准测量的实际精度，因此并非是水准网平差中最为合理的定权方式。为了更为准确地反映地形复杂区域水准测量的实际精度，本文将统计模型引入水准网定权的过程中，再根据水准测量往返测高差较差，推导出适用于地形复杂区域的高差定权公式，最后通过算例验证了这种定权方法的正确性与可行性。

1常规水准网定权与平差原理

对于水准测量数据的处理，一般先按测段的水准路线长度或测站数对高差观测值定权，再采用间接平差的方法，求解出每一测段的高差改正数，进而得出各个水准点的高程平差值，最后根据验后单位权中误差进行验后精度评定。

2水准网平差中定权误差对高差改正数的影响

计算高差改正数是水准网平差的主要目的之一，平差的最终结果是加入高差改正数后的各点高程平差值。所以，欲知水准网中权的设定对平差结果的影响情况，主要应看定权偏差对高差的影响有多大。观测值权的确定一般都会与真实的观测精度存在偏差，这一偏差对控制网平差结果中高差改正数的影响是否显著[4]，下面将从间接平差的误差方程和随机模型入手，分析定权偏差对高差改正数的影响情况。

在不含定权偏差的前提下，由间接平差可得平差后高差改正数

(1)

假设P为含有定权偏差ΔP的权阵，则V和N分别为相对应的存在定权偏差情况下所得到的测段高差改正数和法方程系数阵。有如下关系式：

(2)

当存在定权偏差时，所得高差改正数

V=BN-1BTPl-l=

(3)

(4)

继而可得

(5)

式(5)表示定权误差ΔP对高差改正数V的影响值ΔV计算公式。又因为ΔN=BTΔPB，式(5)可看作ΔP的级数展开，由于ΔP的二次及以上的多项式对ΔV影响可忽略不计，则式(5)可进一步化简为

(6)

由式(6)可以看出，高差观测量改正数偏差ΔV除了与定权偏差ΔP有关外，还与水准网图形构成所决定的系数矩阵B，以及由水准网闭合差和图形构成共同决定的误差方程常数项l有关。因此，可得出如下结论：

高差改正数的计算偏差除了与定权偏差有关外，还与水准网的图形结构及水准路线闭合差有关。因此在存在水准测量误差的情况下，合理优化水准网的网型、严格控制高差观测值的数据质量，将在一定程度上提高水准网平差成果的可信度。

3基于往返测高差较差和地形起伏情况定权的原理与方法

高差观测值的精度往往是由往返测高差不符值来评定的，因为往返测的高差不符值是水准测量中各种误差的集中反映[5]。水准测量的误差主要有：视准轴与水准管轴不平行的误差、水准尺分划误差、水准尺倾斜误差、调焦误差、日照及风力引起的误差、精平误差、照准误差和水准仪及水准尺下沉误差等[6]。在水准测量的每测站高差观测量中都有可能引入这些误差，同时随着视距的增长，观测误差也会增大。

传统水准网平差的定权方法虽顾及到了路线长度或测站数与高差观测误差间的相关关系，但若依此对整个水准网仅采用上述某一种方法定权，则会忽略同一个水准网中不同测段间的地形差异这一重要事实，因而导致定权的结果与实际的观测精度差异较大，会对平差结果的准确性造成不利影响[7]。如在一些地形较为复杂的测区内，会出现山地和平地交替出现的现象，则可能出现某个山地测段的路线长度和某个平地测段的路线长度相等，但它们的测站数却相差甚远的情况。此时，若只按照路线长度定权，则权值大致相等，闭合差分配相当。但它们的高差与测站数的差异是显著的，这明显不是最合理的。不论是山地测段还是平地测段，它们都同属于一个水准网，其所处的地形差异确实较为明显，整网按路线长度或测站数定权都不是最合理的定权方式，而应分类考虑。此外，鉴于目前国家规范规定高等级的水准网均要求往返测量，因此还可探讨根据往返测高差较差推导高差测量的实测精度，并以此确定相应测段高差的权。

3.1　每公里及每测站高差测量中误差计算公式的推导

首先推导由往返测高差较差计算每公里及每测站高差测量精度的公式。设某水准测量中第i测段的往、返测高差是独立等精度的，权值为Pi，往返测高差分别为hi1和hi2，且往返测高差较差为Δi,则有

(7)

由此可求得高差较差的中误差

(8)

式中n为测段数。

由式(8)可按误差传播定律求得单程(往测或返测)的高差中误差

(9)

(10)

(11)

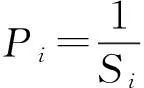
(12)

式(11)和式(12)中Ni是测段i的测站数，Si是测段i的路线长度。

3.2　复杂地形区域定权方法的确定

对于处于复杂地形环境的水准网，不同测段每公里高差的观测精度可能显著不一致，对其整网仅采用按路线长度或测站数定权均不严谨，故定权方式应视水准网所处地形环境的具体情况而定。

设整网总测站数为N总，整网路线总长度为S总，定义统计量

(13)

称K为整体地形因子，对一个特定的水准网，它能反映测区的地形整体起伏状况。

而对于水准网中任意测段i，其测站数为Ni，路线长度为Si，则有

(14)

称Ki为测段i的局部地形因子，它能反映该测段的地形起伏状况。一般认为，对于第i测段，若Ki>K，则认为测段i起伏较大，高差的变化趋势明显，高差观测误差受测站数累积的影响程度大于受路线长度累积的影响程度，所以应按测站数定权。设整网的单位权中误差为μ0，此时观测高差的权应按照下式确定：

(15)

反之，若Kj

(16)

因而可以K作为临界值，将整网的高差观测值分为两类：第一类高差观测误差受路线长度影响显著；第二类高差观测误差受测站数影响显著。

当分别取每测站高差中数的偶然中误差或每公里高差中数的偶然中误差为单位权中误差时，即μ0=mN或μ0=mS，则式(15)和式(16)可变为

(17)

进行了往返测的任何水准网都可以按照式(11)和式(12)估算mN及mS，它们是一个水准网中实际测量精度的最真实体现，往返测较差越多，mN和mS的估值也就越准确。该定权方法特别适用于地形环境复杂、测区地形起伏不定的高精度水准网平差。对地形起伏不显著的测区，由于每公里测站数差异不大，按该方法定权时，仍然是恰当的。

4定权方式合理性的评价

(18)

(19)

则原假设被接受，这时观测值定权的方式是合理的；反之，说明定权方式不得当，平差结果不可靠，应重新考虑定权方式。

5算例及其分析

选择处于某一地形复杂区域的二等水准网实测数据，分别按每测段测站数、测段长度和测段往返测较差定权，然后分别平差计算，再对平差计算结果进行对比，以分析定权方法对水准网平差结果的影响情况，并分别进行方差一致性检验，以验证本文所提定权方法的可行性及合理性。该测区内大多数测段地形起伏较大，其中测段高差最大值接近180m。

5.1　不同定权方法高程和高差平差结果的对比

算例水准网按上述3种定权方法平差后，高程平差值的对比结果如表1所示，高差平差值的差异情况如表2所示。表1和表2中“较差-路线”代表按高差较差定权和按测段路线长度定权的平差结果比较。“路线-测站”代表按测段路线长度定权和按测段测站数定权的平差结果比较；“较差-测站”代表按高差较差定权和按测段测站数定权的平差结果比较。

表1　水准网不同定权方法的高程平差值的

表2　水准网不同定权方法的高差平差值

由表1和表2中的统计结果可知：在所选水准网中，3种定权方法求得的高程与高差平差值的差异的最大分别为4.68mm和1.31mm，说明新旧方法存在差异；根据高差较差定权的平差结果居于两传统方法之间，且与根据测站数定权的平差结果更接近。这是因为该测区环境复杂，测段间地形起伏状况不一致，按测站数和按路线长度定权后各观测值的权比关系有所差异。而根据高差较差定权的方法以各测段的起伏状况的不同而分类定权，并按实际观测精度确定不同起伏测段之间的权比关系。而本算例水准网中起伏大的测段数量相对较多，因此根据高差较差定权和根据测站数定权的平差结果更接近。

5.2　不同定权方法验后精度的对比

上述水准网分别按3种定权方法平差后，测段高差中误差和各水准点高程中误差的相关统计数据如表3所示。

表3　水准网不同定权方法平差后精度比较　 mm

由表3可知：在本算例的水准网中，分别按照测站数、高差较差和路线长度3种方法定权并平差后的高程中误差和高差中误差总体上相差不大。根据高差较差定权后的高程和高差中误差的平均值与根据测站定权的平差精度更为接近，这是由于在整个水准网中，大起伏的测段占多数。根据表3的比较结果，可以认为根据高差较差定权对传统定权方法精度评定中的极端现象起到了一定的中和作用，更能反映控制网的实际精度状况。