基于蚁群算法的机器人切割轨迹规划

2015-12-31童安璐宗光华

机械工程与自动化 2015年4期

童安璐，宗光华，王巍

（北京航空航天大学机械工程及自动化学院，北京 100191）

0 引言

机器人切割路径执行顺序问题即切割轨迹规划问题，实际上可以理解为一个旅行商问题（Traveling Salesman Problem，TSP）。TSP是经典的组合优化问题，人们对求解TSP问题已经进行了大量的研究，提出了许多用以解决该类问题的进化算法，如遗传算法、退火算法、贪婪算法等。20世纪90年代，意大利学者Dorigo和Colorni等［1］人首先提出蚁群（Ant Colony System ACS）算法，该算法具有较强的鲁棒性、较好的全局优化能力和分布计算能力，同时还容易与其他方法相结合，特别适合于求解困难的组合优化问题［2－3］。

1 蚁群算法基本原理

为了阐述基本蚁群算法对TSP问题的描述，首先设m为蚁群中蚂蚁的数量，ρ为信息素挥发率，τij为城市i和j之间的信息素量，dij为城市i和j之间的距离。信息素量τij可以表示为：

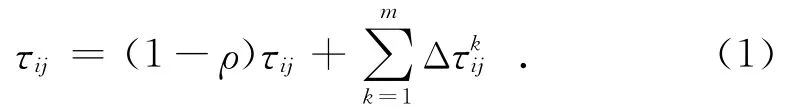
式（1）中加号左边为残余信息素量，右边为更新的信息素量。蚂蚁觅食过程中，随着时间的推移，以前留下的信息素逐渐挥发，信息素挥发率ρ的值介于0～1之间。

其中：Q为一个常数；Lk为第k只蚂蚁完成觅食的行走路径长度。第k只蚂蚁对城市i和j间信息素的更新量与该蚂蚁在旅行过程中总的行走距离成反比。

每一只蚂蚁都面临着下一个路径的选择问题，下一个路径选择机制描述如下：当蚂蚁k处在城市i时，将蚂蚁下一个可选城市集表示为一个集合N（sp）；当前城市为i，cij表示蚂蚁选择城市j，cil表示蚂蚁选择城市l。参数α和β是常数，控制着信息素τ与启发式信息η的比例，蚂蚁k选择从城市i到j的概率为：

式（3）中，当j不属于可选城市集时，蚂蚁选择下一城市j的概率为0，而当j处于可选城市集时，概率是信息素τ与启发式信息η的函数，第一行分母表示当前城市i的所有可选城市路径集合中τ与η多项式之和。启发式信息η可表示为：

2 机器人切割轨迹规划问题描述

2.1 轨迹分析

将蚁群算法应用于机器人切割轨迹规划需要解决算法中的城市与轨迹规划中的轨迹的对应问题。

经过分析发现，用户选择的切割路径主要是以线、圆、圆弧、样条等基本图形信息为主，这些轮廓信息可以归纳为有若干节点的开放式轨迹和由若干节点围成的封闭式轨迹［4］。无论是开放式轨迹段，还是封闭式轨迹段，所有轨迹都是有向轨迹，都拥有轨迹的起点和终点。把一段轨迹视为蚁群算法中的一个城市，且限定只能轨迹终点指向轨迹起点，那么两个城市间的距离有两个值，需要对城市距离进行二值化修改。

此外与蚁群算法不同的是，所有的切割路径都是相邻的，即所有的城市都属于相连的城市，不存在间接连接的城市。

2.2 规划目标分析

将蚁群算法应用于机器人切割轨迹规划还需要针对机器人切割实际情况对规划目标进行分析。

首先单个城市轨迹起点到终点的长度不应计入蚂蚁行走总长度。轨迹规划的目标是对走刀空程总长进行优化，而轨迹路径是有效切割路径，不属于空程长度，蚁群算法中应忽略其影响。

其次机器人切割轨迹规划与旅行商不同点在于旅行商在走完所有城市之后还应回到出发城市，最终构成一个路径回路，而机器人切割轨迹规划无需回到出发城市，只是在所有城市之间选择一条单向的最优路径。

3 算法设计

设计蚁群算法流程如图1所示，将其作为一个模块嵌入机器人切割软件中。具体流程如下：

（1）输入参数为用户选择的图元链vector容器，使用该容器初始化城市数目相关参数，包括城市间距离数组、蚁群数目、城市间信息素数组。其中城市间距离数组根据图元链起点和终点的不同值进行相应初始化，每两个城市间距离有两个值。

（2）进入迭代求解过程，每次迭代都要对蚁群的m只蚂蚁进行路径求解。每只蚂蚁的求解策略如下：首先初始化访问城市数据，同时随机选择一个城市作为出发城市；然后依据城市选择策略选择适当的城市，直到完成所有的城市访问；最后记录下该蚂蚁访问的路径节点及长度信息。

为防止蚁群算法过快收敛于局部最优解，本算法的信息素更新只在一个迭代完成之后进行。一个迭代步中，所有蚂蚁的城市选择策略基于上一个迭代步遗留信息素量。引入参数fij来描述城市选择策略：其中：Vi为未访问的节点集合。

计算所有n个城市fij之和∑fij，并在0与∑fij之间取一个随机数temp，使用轮盘赌实现下一个城市输出［6］。第k次转动轮盘，temp减去对应本次转动的fik，直到temp小于0。由于temp均匀地落在0～∑fij之间，选择每一个城市的概率符合式（3）。

（3）完成一次迭代，对全局信息素进行更新。根据式（2）计算每只蚂蚁的数组，最后叠加上挥发后的原有信息素，实现城市间信息素的全局更新。信息素挥发系数ρ与常数Q根据文献［5］分别取为0.7与100。

（4）到当前迭代次数为止，所建立的所有局部最优解中，值最小的解作为当前迭代次数的全局最优解。

图1 设计蚊群算法流程

4 实验验证

由2.1节叙述可知，把一段轨迹视为蚁群算法中的一个城市，则城市间的距离有两个值。轨迹起点、终点重合，两个值相同，若不重合，则两个值不同。切割轨迹起点、终点重合与否对不同算法轨迹规划的效果有一定影响。为验证本文改进蚁群算法对两种情况均有较强适应性，做如下实验。

首先验证切割路径起点和终点重合时，蚁群算法的全局较优性。定义30个城市，城市坐标即为切割路径起点、终点的重合点，坐标数据见表1。

引入两种路径求解算法：图元顺序求解和最近距离求解。图元顺序即按照城市坐标的原始顺序计算空程总长，表1中城市间距离即为空程长度，从城市1开始，依次求解30个城市距离即可。最近距离即按照单个城市局部最优解的顺序计算空程总长，从城市1开始寻找下一个最近距离城市，计算空程长度，然后再访问下一个最近距离城市，叠加空程长度，直到所有城市访问完毕。蚁群算法与图元顺序求解、最近距离求解结果对比见图2。图元顺序空程总长850.152km，最近距离空程总长427.340km，蚁群算法空程总长371.725km，蚁群算法求解结果比图元顺序求解结果有着显著优化，比最近距离求解结果优化了13%。

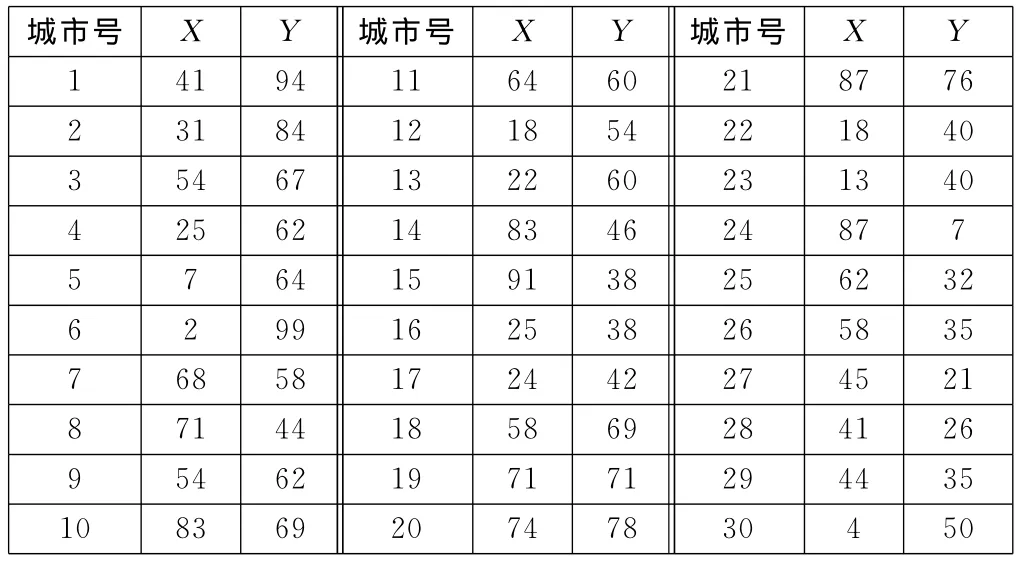
表1 城市坐标数据 km

其次，切割路径起点、终点不相同时，定义10段切割轨迹代表10个城市，轨迹编号与轨迹方向见图3（a）中原始数据。蚁群算法求解的最短路径结果与按图元顺序以及按最近距离求解的结果对比见图3。图元顺序空程总长227.786km，最近距离空程总长175.652km，蚁群算法空程总长145.325km，蚁群算法求解结果比图元顺序求解结果有着显著优化，比最近距离求解结果优化了17%。

5 结束语

考虑到机器人切割过程与TSP求解过程有所不同，因此本文对机器人切割轨迹和规划目标进行了分析，并设计了符合机器人切割加工实际的改进蚁群算法。通过与图元顺序以及按最近距离求解的算例仿真对比显示，基本蚁群算法具有较明显的优势，同样切割路径下，可以得到空行程更短的加工路径。由于基本蚁群算法容易收敛于局部最优解，因此想要得到更优的解，有待进一步研究。