基于CLO3D的织物悬垂性模拟影响因素分析

2015-12-31王会威

纺织科技进展 2015年5期

王会威，张辉

（北京服装学院，北京 100029）

织物悬垂性对服装外形美观有一定程度的影响。目前对其进行的研究大多集中在材料的力学性能与悬垂性的关系上，并利用织物的结构参数及力学性能等指标建立模型，利用3D图形接口OpenGL在计算机中模拟显示织物的悬垂形态［1-6］。随着三维技术在服装设计与展示领域的应用越来越受到重视，如何提高服装在三维环境下模拟真实感就变得十分必要。在三维环境中，材质参数、光照参数及材料悬垂感的准确模拟直接影响着服装的真实感；对柔性材料的模拟往往是以质点、网格模型的方式进行，所需设置的参数与真实织物的力学参数有很大区别。因此研究三维环境下面料的属性参数与悬垂性能的关系，对于比较准确地模拟三维虚拟服装有很大帮助，但在这方面的研究报道还比较少。本文旨在探究三维环境下的各项属性参数与悬垂系数的关系，希望为利用三维软件模拟织物悬垂效果及更逼真地模拟服装的悬垂形态提供参考。

1 实验方法

1.1 选择模拟影响因素

本研究在三维软件CLO3D中进行。由于CLO3D中包含多个用于设置织物特性的属性参数，通过前期摸索，选取了与模拟织物悬垂形态有关的8个属性参数：Stretch-weft（纬纱弹力），Stretch-warp（经纱弹力），Shear（剪切），Bending-weft（纬向弯曲），Bendingwarp（经向弯曲），Buckling ratio（曲率），Buckling stiffness（弯曲刚度），Density（密度）。需要注意的是，虽然在三维系统中的属性参数与真实织物结构参数及力学性能的名称有些相似，但这些指标并不能与实际织物的参数一一对应，其数值范围为0～99，且没有单位，无法直接应用面料的测量数据。

经过前期的预实验发现，系统的织物属性参数值在过大或过小时，模拟织物将呈现出异于真实织物的悬垂形态。因此参考系统内预设织物的属性参数取值范围经多次尝试、分析，对8个参数较合理的间隔取值见表1。由于选取的参数个数较多，为了研究悬垂系数的主要影响因素，本文先不考虑模拟织物自身经、纬向上力学性能及结构参数的异向性，统一经纬向上的参数值，即令Stretch-weft与Stretch-warp、Bending-weft与Bending-warp的取值相同。最后对取值结果进行排列组合，最终得到972个属性参数组合。

表1 织物属性参数的取值

1.2 建立回归模型

利用Rhino软件创建的悬垂仪模型见图1，根据织物悬垂性测量的国家标准，将模拟织物圆直径设定为24cm，夹持盘直径设定为12cm。将悬垂仪模型导入CLO3D系统中，按照表1中的各属性参数值进行排列组合，依次在各个属性参数组合下进行织物悬垂模拟实验；待模拟织物悬垂形态稳定后，利用北京服装学院张辉博士研发的模拟织物悬垂系数测量软件求解模拟织物的悬垂系数，最终得到972组实验数据。织物悬垂模拟效果示意图见图2，利用SPSS软件分析出对模拟织物悬垂系数影响较大的CLO3D属性参数，并求出悬垂系数的回归模型。

图1 悬垂仪模型

图2 织物悬垂形态模拟效果图

1.3 测试方法

纺织品悬垂性测定根据国家标准GB／T 23329-2009进行，悬垂系数越小，织物的悬垂性越好。悬垂系数计算方法如下：

式中D——为悬垂系数（%）；As——试样悬垂后的投影面积（cm2）；A0——未悬垂试样的初始面积（cm2）；Ad——夹持盘面积（cm2）。

2 结果与讨论

2.1 模拟织物悬垂系数与属性参数的相关性

为了分析影响模拟织物悬垂系数的主要因素，首先利用统计分析软件SPSS对实验结果进行相关分析。相关系数是描述两者间线性关系强弱程度和方向的统计量，取值在1和-1之间，绝对值越大说明两者关系越密切。悬垂系数与6个属性参数的相关分析结果见表2。

表2 悬垂系数与6个属性参数的相关分析结果

从表2可知，悬垂系数与Stretch、Shear、Bending和Density 4个属性参数存在线性关系，并且相关系数为0的假设检验成立的概率均小于0.001。模拟织物的悬垂系数与Stretch、Shear为弱相关，与Density呈中度相关，与Bending为高度相关。模拟织物的悬垂系数与Buckling Ratio、Buckling Stiffness两个变量不相关。

2.2 模拟织物悬垂系数的回归方程

多元回归分析是根据多个自变量的最优组合建立回归方程来预测因变量的分析方法。将模拟织物的悬垂系数作为因变量，以Bending为X1、Density为X2、Shear为X3、Stretch为X4作为自变量，建立线性回归模型。回归分析结果见表3。

表3 回归分析结果

由表3可知，常量及4个面料属性参数的偏回归系数为0的假设检验的显著性水平值均小于0.001，得到多元线性回归方程为：

回归方程（2）中各自变量之间没有出现共线性问题，回归方程的修正R2值为0.944，大于0.8，表明拟合程度好；自变量Bending及Density对悬垂系数的影响较大。

2.3 主要参数对模拟织物悬垂系数的影响

在模拟织物悬垂系数的回归方程（2）中，最重要的两个自变量分别为Bending和Density，为研究两者对悬垂系数的共同影响，在一定范围内改变Bending和Density两者的数值，观察并记录悬垂系数的变化。其他属性参数取中间值，即Stretch取值35、Shear取值30、Buckling ratio和Buckling stiffness均取值45。此时，悬垂系数与这两个主要属性参数的关系曲线如图3所示。

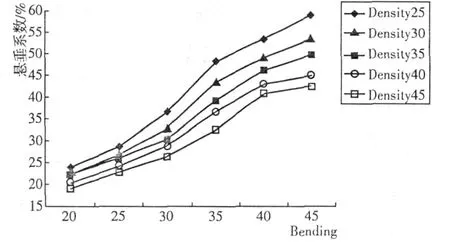
图3 Bending和Density共同作用下的悬垂系数曲线图

由图3可看出，Bending和Density对仿真织物悬垂系数的影响显现出一定的规律性：不考虑Density的影响，Bending越大，悬垂系数越大；不考虑Bending的影响，Density越大，悬垂系数越小。Bending值处于25～35之间时，随着Density的增大，悬垂系数的增大趋势逐渐减小；Bending值处于35～45之间时，随着Density的增大，悬垂系数的增大趋势趋于走平。