环形势阱中旋转玻色爱因斯坦凝聚体的基态

刘 燕, 张素英（山西大学理论物理研究所,山西太原 030006）

环形势阱中旋转玻色爱因斯坦凝聚体的基态

刘 燕, 张素英
（山西大学理论物理研究所,山西太原 030006）

应用托马斯－费米近似和虚时演化数值方法研究环形势阱中旋转玻色爱因斯坦凝聚体的基态密度分布.当增加其旋转角频率,或者增加环形势阱的宽度及相应的中心高度,凝聚体基态密度分布均从涡旋晶格相转变为巨涡旋相.当旋转角频率为零时,增加环形势阱的宽度及相应的中心高度,凝聚体基态密度分布从一个圆盘变为圆环.解析结果与数值结果相互吻合.

托马斯－费米近似；中心洞；巨涡旋

0 引言

近年来,有关冷原子研究的快速发展以及实验技术的不断提高实现了对各种不同形式的束缚外势的调控,如谐振子势、光晶格势以及环形势等[1－2].对不同束缚外势阱中的旋转玻色爱因斯坦凝聚体（BEC）的理论研究也取得了很大的进展.对于谐振子势阱中的旋转玻色爱因斯坦凝聚体,当旋转角频率Ω趋近于或者大于势阱束缚频率ω⊥时,凝聚体的托马斯－费米近似半径发散[3－4].若在谐振子势的基础上加入一个四次势,则可以克服这一缺陷使托马斯－费米近似半径在Ω＞ω⊥时继续收敛,且随着旋转角频率的增大,凝聚体的基态密度分布呈现出各种新奇的涡旋拓扑结构[5－10].改变凝聚体粒子间的相互作用强度,拓扑结构也会发生相应的变化[11－17].除此之外,凝聚体的基态密度分布还和束缚势阱的结构有关.对于旋转环形势阱中的玻色爱因斯坦凝聚体,当粒子间互作用强度和势阱旋转角频率一定时,调节环形势阱的宽度及相应的中心高度,凝聚体的基态密度分布必然也会出现新的涡旋相.我们考虑单分量玻色爱因斯坦凝聚体束缚在如下形式的环形势阱中且势阱以角速度Ω＝Ωz绕z轴旋转：

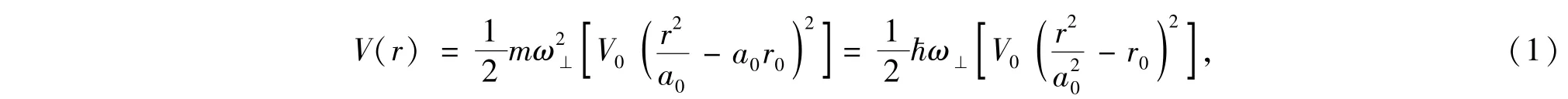
势阱的最低点坐标为（±a0,0）,中心最高点坐标为（0,/2）,其中a0＝,r表示径向坐标,V0,r0是无量纲化的常数,可以调整势阱的宽度及相应的中心高度.我们首先应用托马斯－费米近似理论求解上述环形势阱中的玻色爱因斯坦凝聚体在如下三种情况下的基态密度分布情况：①势阱的宽度及相应的中心高度一定,增大其旋转角频率；②势阱的旋转角频率一定,增大其宽度及相应的中心高度；③令势阱旋转角频率为零,增大其宽度及相应的中心高度.进一步运用虚时演化数值方法模拟这三种情况下凝聚体的基态密度分布情况,并将其同解析结果进行比较.

此外,我们还可以保持旋转角频率及势阱宽度不变,数值模拟凝聚体的基态密度分布随势阱中心高度增加的变化.但是,如何解析求解量子化涡旋数目与旋转角频率及势阱结构的关系还需进一步研究.

1 理论模型

绝对零度下受外势束缚的玻色爱因斯坦凝聚体可以用一个波函数ψ来描述,它满足如下非线性薛定谔方程

其中as是一个正的s波散射长度,描述凝聚体粒子间的排斥相互作用.如果外势阱绕z轴以Ω ＝Ωz的角速度旋转,则波函数ψ满足如下非线性薛定谔方程

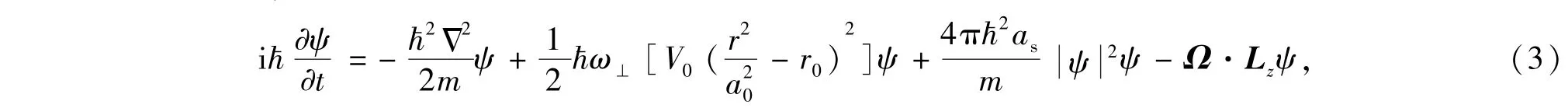
其中Lz＝r×p＝－i h－r×Δ＝－i h－（xƏy－yƏx）是角动量算符的z分量.波函数ψ满足如下归一化条件

N为总粒子数.将波函数分解为ψ（x,y,t,z）＝ϕ（x,y,t）φ（z）,令＝ψa0/,＝ω⊥t,＝r/a0,＝Ω/ω⊥,＝Lz/h－,在方程（3）中作变量代换并将波浪线去掉,则得到如下准二维无量纲化的非线性薛定谔方程：

其中g＝4πηNas,η＝∫d z｜φ（z）｜4∫dz｜φ（z）｜2,波函数ϕ满足归一化条件

无量纲化之后的外势阱的示意图及沿x轴的截面如图1所示.

图1 环形势示意图及沿x轴的截面图Fig.1 Schematic of annular potential and cross section of potential at y＝0

相应地,与上述非线性薛定谔方程对应的拉格朗日函数为

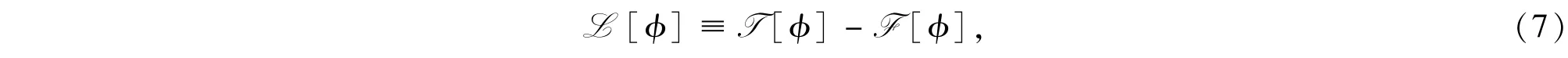
其中,

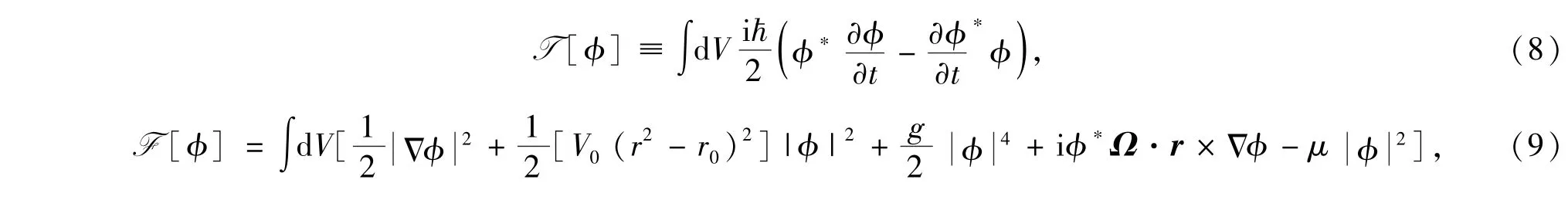
化学式μ为拉格朗日乘子.

2 托马斯－费米近似

其中相位梯度 Δθ＝v＝Ω×r表示超流速.在托马斯－费米近似中,通常忽略曲率密度上述自由能函数对求变分可得如下托马斯－费米密度

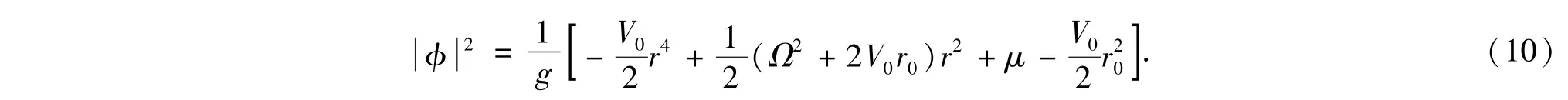
2.1 出现中心洞的临界条件

由（10）式中托马斯－费米密度为零可得

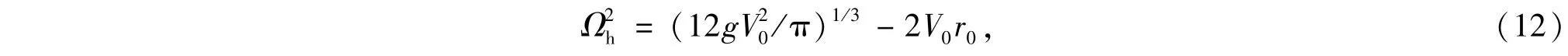
或者

2.2 有中心洞的涡旋晶格的性质

根据归一化条件（6）可得

下面我们分三种情况分别讨论旋转环形势阱中玻色爱因斯坦凝聚体的基态密度分布随旋转角频率及势阱结构的变化情况.

情况1 势阱宽度及相应的中心高度一定,增大其旋转角频率

结合（12）,（15）,（16）式,可得

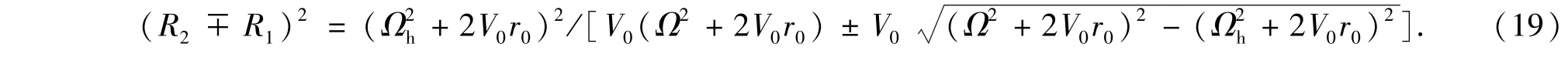
当Ω→Ωh时,d＝R2－R1≈R2,R≈d/2,随着Ω的增大,圆环平均半径R增大,而宽度d在减小.

情况2 势阱旋转角频率一定,增大其宽度及相应的中心高度

结合（13）,（15）,（16）式,可得

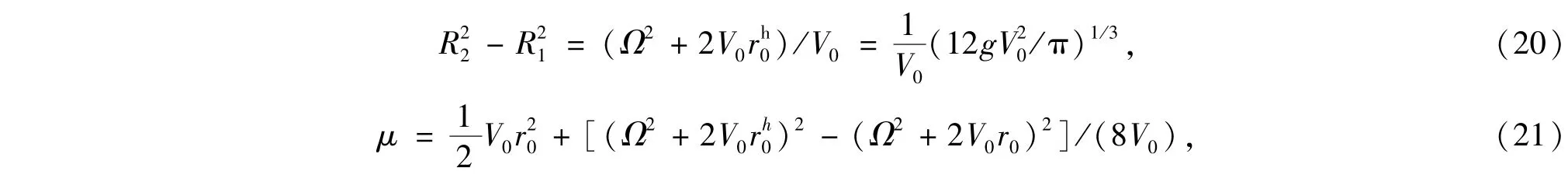
只有r0＞时,才能满足μ＜/2.由式（14）和式（20）得

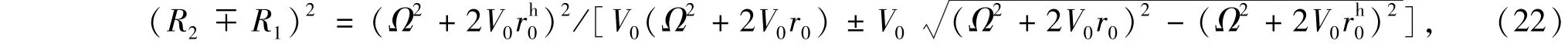
当r0→时,d＝R2－R1≈R2,R≈d/2,随着r0的增大,R增大,d减小.

情况3 令势阱旋转角频率为零,增大其宽度及相应的中心高度

若旋转角频率为零,则由公式（13）可知出现中心洞的临界条件为

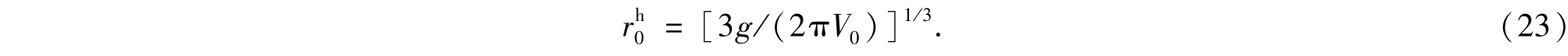
此时

当r0→时,d＝R2－R1≈,R＝d/2,随着r0的增大,R增大,d减小.

上述三种情况下无量纲化的环形势阱V（r）＝V0（r2－r0）2/2束缚的玻色爱因斯坦凝聚体的托马斯费米近似半径在任何参数条件下都是收敛的.而无量纲化的环形势阱V（r）＝V0（r－r0）2/2束缚的玻色爱因斯坦凝聚体只有在Ω2＜V0的条件下才能满足托马斯费米近似半径收敛[18].

3 数值模拟

运用虚时演化数值方法模拟无量纲化的两维非线性薛定谔方程（5）描述的凝聚体的基态密度分布并同解析结果进行比较[19－20].首先,我们选取g＝100,V0＝0.5,r0＝3,对于不同的旋转角频率Ω,凝聚体的基态密度分布如图2所示.当Ω＝1.4时,凝聚体基态密度分布由圆盘变为圆环,随着旋转角频率的增大,圆环平均半径增大,宽度变窄,量子化涡旋数目增多且最终全部包含在中心洞的内部形成巨涡旋；其次,选取g＝100,V0＝0.5,Ω＝2,对于不同的r0,凝聚体的基态密度分布如图3所示,当r0＝1.5时,凝聚体基态密度分布由圆盘变为圆环,增大r0,凝聚体基态密度分布变化情况同增大旋转角频率Ω相似；最后,考虑强相互作用下凝聚体的基态密度分布随r0的变化情况,取g＝1 000,V0＝0.5,Ω＝2,对于不同r0凝聚体的基态密度分布如图4所示,当r0＝7时,密度分布由圆盘变为圆环,增大r0,圆环平均半径增大,宽度变窄,量子化涡旋数目增多且一部分包含在中心洞的内部形成巨涡旋,一部分呈链状均匀的排列在环的内部.图5显示,在形成巨涡旋的三种不同条件下,凝聚体基态密度分布的解析结果同数值结果相互吻合.另外,我们考虑角频率Ω＝0时凝聚体基态密度分布随r0增大的变化情况,图6显示g＝100,V0＝0.5,r0＝7和g＝1 000, V0＝0.5,r0＝12两种情况下,凝聚体的基态密度分布都没有出现量子化涡旋,但都出现了中心洞,且均与解析结果相一致.

图2 g＝100时不同Ω对应凝聚体的基态密度分布和相位（第一行为密度分布,第二行为相位）Fig.2 Ground state density profiles and phases for different angular velocities with g＝100（The first row is ground state density profiles.The second row is corresponding phase plots.）

图3 g＝100时,不同r0对应凝聚体的基态密度分布和相位（第一行为密度分布,第二行为相位）Fig.3 Ground state density profiles and phases for different r0with g＝100（The first row is the ground state density profiles.The second row is corresponding phase plots.）

图4 g＝1 000时,不同r0对应凝聚体的基态密度分布和相位（第一行为密度分布,第二行为相位）Fig.4 Ground state density profiles and phases for different r0with g＝1 000（The first row is ground state density profiles.The second row is corresponding phase plots.）

4 结论

通过托马斯－费米近似和虚时演化方法求解可知,当粒子间相互作用强度和环形势阱结构一定时,增大势阱旋转角频率到某一临界值Ωh或当粒子间相互作用强度和势阱旋转角频率一定时,增大控制环形势阱宽度及相应中心高度变化的参量r0到某一临界值,凝聚体基态密度分布均从圆盘变为圆环.继续增大Ω或者r0,圆环平均半径增大,而宽度变窄,量子化涡旋数目增多.当粒子间相互作用较弱时,量子化涡旋会随着

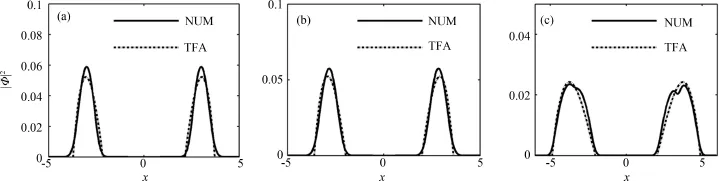
图5 三种不同条件下,凝聚体基态密度分布沿x轴的截面（a）g＝100,V0＝0.5,Ω＝2.5,r0＝3,（b）g＝100,V0＝0.5,Ω＝2,r0＝4.5,（c）g＝1 000,V0＝0.5,Ω＝2,r0＝10Fig.5 Cross sections of ground state density profiles of condensates along x axis, （a）g＝100,V0＝0.5,Ω＝2.5,r0＝3,（b）g＝100,V0＝0.5,Ω＝2,r0＝4.5,（c）g＝1 000,V0＝0.5,Ω＝2,r0＝10

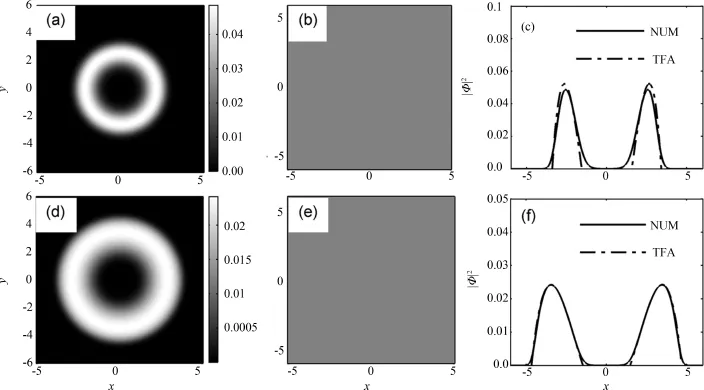
图6 Ω＝0时凝聚体的基态密度分布（a）,（d）、相位（b）,（e）及密度沿x轴截面的分布（c）,（f）：（a）,（b）,（c）g＝100,V0＝0.5,r0＝7；（d）,（e）,（f）g＝1 000,V0＝0.5,r0＝12Fig.6 Ground state density profiles（a）,（d）,phase plots（b）,（e）and cross sections of density profiles of condensates along x axis（c）,（f）withΩ＝0：（a）,（b）,（c）g＝100,V0＝0.5,r0＝7；（d）,（e）,（f）g＝1 000,V0＝0.5,r0＝12

Ω或者r0的增大全部包含在中心洞中形成巨涡旋,当粒子间相互作用较强时,量子化涡旋随着Ω或者r0的增大一部分包含在中心洞中形成巨涡旋,一部分呈链状均匀排列在环的内部,这里我们只给出了其随r0增大的变化情况.当旋转角频率为零时,增大r0到某一临界值,凝聚体基态密度分布也会从圆盘变为圆环,但不会出现量子化涡旋.凝聚体基态密度分布的解析结果同数值结果相互吻合.可见,旋转是产生量子化涡旋的直接因素.当旋转角频率为零时,没有量子化涡旋；当旋转角频率不为零时,增大旋转角频率或者增大势阱宽度及相应的中心高度,量子化涡旋的数目都会增多,且最终形成巨涡旋.

[1] Bretin V,Stock S,Seurin Y,Dalibard J.Fast rotation of a Bose-Einstein condensate[J].Phys Rev Lett,2004,92：050403.

[2] Ryu C,Andersen M F,Clade P,Natarajan V,Helmerson K,PhillipsW D.Observation of persistent flow of a Bose-Einsteincondensate in a toroidal trap[J].Phys Rev Lett,2004,99：260401.

[3] Haljan PC,Coddington I,Engels P,Cornell E A.Driving Bose-Einstein-condensate vorticity with a rotating normal cloud [J].Phys Rev Lett,2001,87：210403.

[4] Stringari S.Phase diagram of quantized vortices in a trapped Bose-Einstein condensed gas[J].Phys Rev Lett,1999,82：4371.

[5] Fetter A L.Rotating vortex lattice in a Bose-Einstein condensate trapped in combined quadratic and quartic radial potentials [J].Phys Rev A,2001,64：063608.

[6] Lundh E.Multiply quantized vortices in trapped Bose-Einstein condensates[J].Phys Rev A,2002,65：043604.

[7] Kasamatsu K,Tsubota M,Ueda M.Giant hole and circular superflow in a fast rotating Bose-Einstein condensate[J].Phys Rev A,2002,66：053606.

[8] Jackson A D,Kavoulakis G M,Lundh E.Phase diagram of a rotating Bose-Einstein condensate with anharmonic confinement [J].Phys Rev A,2004,69：053619.

[9] Fetter A L,Jackson B,StringariS.Rapid rotation ofa Bose-Einstein condensate in a harmonic plus quartic trap[J].Phys Rev A,2005,71：013605.

[10] Kim JK,Fetter A L.Dynamics of rapidly rotating Bose-Einstein condensates in a harmonic plus quartic trap[J].Phys Rev A, 2005,72：023619.

[11] Fu H,Zaremba E.Transition to the giant vortex state in a harmonic-plus-quartic trap[J].Phys Rev A,2006,73：013614.

[12] Aftalion A,Mason P.Rotation ofa Bose-Einstein condensate held under a toroidal trap[J].Phys Rev A,2010,81：023607.

[13] Jeng B W,Wang Y S,Chien C S.A two-parameter continuation algorithm for vortex pinning in rotating Bose-Einstein condensates[J].Comput Phys Comm,2013,184：493－508.

[14] Song T L,Ma Y L.Finite vortex numbers and symmetric vortex structures in a rotating trapped Fermi gas in the BCS-BEC crossover[J].Eur Phys JB,2011,82：303－311.

[15] Song T L,Ma C R,Ma Y L.Vortex lattices in a rotating Fermisuperfluid in the BCS-BEC crossover withmany Landau levels [J].Ann Phys,2012,327：1933－1947.

[16] HuaW,Liu X.Improved shootingmethod for Gross-Pitaevskii equation：Interference of three Bose-Einstein condensates[J].Chinese JComput Phys,2011,28（6）：922－926.

[17] Che L,Luo X,Su M.Interference of three Bose-Einstain condensates in one-dimensional time-dependent Gross-Pitaevskii equation[J].Chinese JComput Phys,2011,28（3）：463－468.

[18] Jin J J,Zhang S Y,Han W,Wei Z F.The ground states and spin textures of rotating two-component Bose-Einstein condensates in an annular trap[J].JPhys B：AtMol Opt Phys,2013,46：075302

[19] Antoine X,Bao W,Besse C.Computationalmethods for the dynamics of the nonlinear Schrödinger equations[J].Comput Phys Comm,2013,184：2621－2633.

[20] Dalfovo F,Stringari S.Bosons in anisotropic traps：Ground state and vortices[J].Phys Rev A,1996,53：2477.

Ground States of Rotating Bose-Einstein Condensates in an Annular Trap

LIU Yan, ZHANG Suying
（Institute of Theoretical Physics,Shanxi University,Taiyuan 030006,China）

Thomas-Fermi approximation（TFA）and imaginary-time propagation method are used to study ground states of rotating Bose-Einstein condensates in an annular trap.Ground state density profiles of condensates experience a transition from vortex lattice phase to giant vortex phasewith increase ofangular frequency orwith increase ofwidth and center heightof trap potential.Particularly, ground state density profiles change from a disc shape into an annulus shape with the increase of width and center height of trap potential,when angular frequency is zero.Finally,comparison between ground state density profiles,obtained by analyticalmethod and numericalmethod ismade.They coincide with each other.

Thomas-Fermi approximation；central hole；giant vortex

1001-246X（2015）06-0744-07

O469

A

2014－12－05；

2015－02－13

国家自然科学基金（91430109）,高等学校博士学科点专项科研基金（20111401110004）及山西省自然科学基金（2014011005-3）资助项目

刘燕（1988－）,女,硕士生；研究方向：计算物理,E-mail：zhangsy＠sxu.edu.cn