声波在双层非线性介质中传播的二极管现象

郭凤丽, 胡冬生,通讯作者：胡冬生,E-mail：dongshenghu＠nuaa.edu.cn,电话：3803766, 徐 江（.南京航空航天大学理学院,南京 06；.南京航空航天大学材料学院,南京 06）

声波在双层非线性介质中传播的二极管现象

郭凤丽1, 胡冬生1,∗∗通讯作者：胡冬生,E-mail：dongshenghu＠nuaa.edu.cn,电话：13218037266, 徐 江2
（1.南京航空航天大学理学院,南京 211106；2.南京航空航天大学材料学院,南京 211106）

假设声波在双层一维非线性系统中传播时线性部分满足波动方程,非线性部分类似于非线性薛定谔方程的非线性部分.对该模型正反两个方向分别入射相同的声波计算透射率发现：一定频率及强度的声波在模型中具有单向透过性,表现出声二极管的行为；随着非线性强度差异的增强,单向导通性显著提高.

非线性系统；声波；整流；二极管

0 引言

作为第一个对能量产生整流作用的器件——电子二极管,其发明具有里程碑式的意义.此后,对其它运动形式可能具有二极管现象的研究受到了很大程度的关注[1－14].二极管现象是指某种形式的能量沿特定的方向可以传输,而沿着相反的方向则被阻碍的现象.新加坡的李保文课题组在理论上研究了具有非线性的Frenkel-Kontorova链的不对称热传输现象,提出了可实现单向热传导的“热二极管”理论模型[1－2].其后,美国加州州立大学伯克利分校的Chang等人及日本早稻田大学的Kobayashi等人通过实验制备出了热整流器件[3－4].2005年,美国加州州立大学圣地亚哥分校的 Nesterenko课题组在实验中发现了孤立波在通过由一系列由钢球组成的非线性系统时出现了反常的反射现象,实现了对孤立波的整流[5].还有学者用非线性传输线作为能量单向传输的研究[6].在“光二极管”方面,已经有了大量的理论和实验研究.光子晶体是由两种不同介电材料组成的具有周期性的多层结构.在光子晶体中引入缺陷可以使某些频段光波的透射强度显著提高[15].基于非线性会使光子晶体禁带边界移动,Scolora等人于1994年设计出第一个光子晶体全光二极管[7]（即脉冲从正向能够很好地传输,而从相反的方向却几乎完全反射）.之后,Mingaleev等人提出一种利用光子晶体线缺陷设计全光二极管的设想[8].2005年,有人提出利用单个非对称光子晶体的缺陷来设计全光二极管[9－10].

声波作为波动的一种普遍的存在形式,若能实现象电子二极管那样对声能量进行整流的声学器件,会对声学的理论研究、声学的器件制造及应用产生重大的影响.由于线性条件下互易原理的限制[12],如何在声学系统中实现声整流效应始终是一个难题.在声学理论中线性声学系统显然满足了互易原理,这就决定了在任何一个线性声学系统中声能量的透射都不会产生二极管现象.声波的二极管现象只有在非线性强度不同的多层结构中才可能产生[12].2009年,南京大学程建春课题组从理论上提出：由超晶格结构与强声学非线性媒质组成的系统具有声二极管现象[13],并在2010年成功制造出声二极管的示意性样品[14].该样品由超声造影剂微泡溶液与一个超晶格（水与玻璃的层叠）构成,实验结果表明：在声整流频段内,声二极管样品表现出了极高的整流效率,最大整流比接近1万倍.本文以一个玩具模型来演示声波在非线性系统中传播时具有二极管现象,为实现声二极管提供一种可能性.

1 模型与方法

研究对象是两种非线性材料组成的一维系统,如图1所示.为研究声波在其中传播时的透射性质,假设该一维系统的两端由均匀的线性部分连接,声波由左端入射右端出射,或由右端入射左端出射.

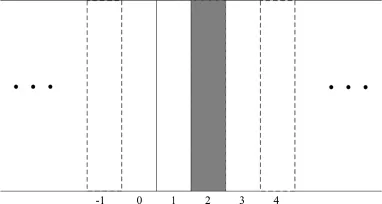
图1 两种非线性材料组成的一维系统的示意图.1、2两层是非线性强度不同的材料,左右由线性材料连接Fig.1 Schematic of one-dimensional system consists of two nonlinearmaterials.Layer 1 and Layer 2 are different nonlinearmaterials,which are connected with linearmaterials in both sides

波在两端均匀的线性部分中满足波动方程

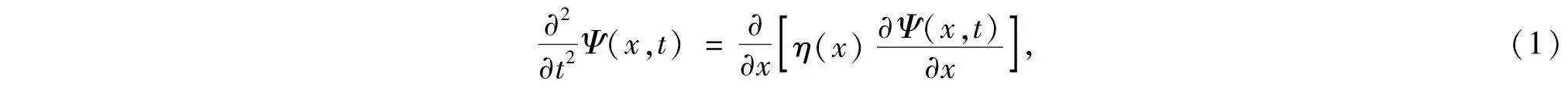
其中η（x）＝e（x）/m是介质刚度与平均密度的比值,波函数Ψ（x,t）时空分离后可写为：Ψ（x,t）＝ψ（x）e－iωt.在双层非线性系统中,我们假设它的非线性部分满足非线性薛定谔方程的非线性部分,即满足

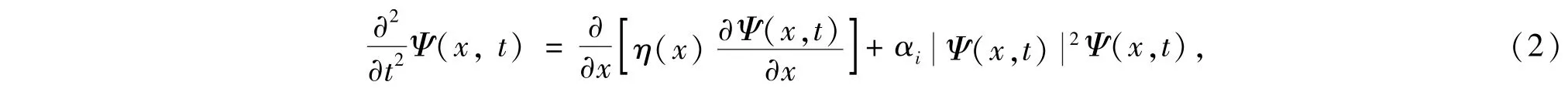
其中αi表示第i介质层处的非线性强度.

首先用有限差分方法将连续的线性波动方程转化为差分方程.我们把空间进行离散化,设厚度Δx为一个单位.用Ψn和ηn分别表示离散化后的波函数和介质刚度与平均密度的比值,其中n即为离散化后的编号.用向后一阶差商和中心二阶差商将方程中空间部分离散化,可得

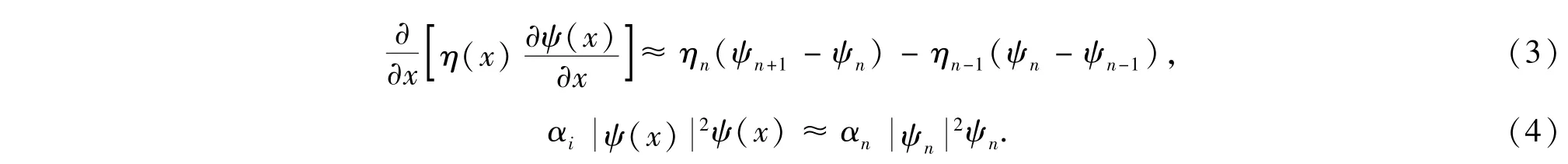
因此,线性的和非线性的一维离散化的波动方程可分别表示成

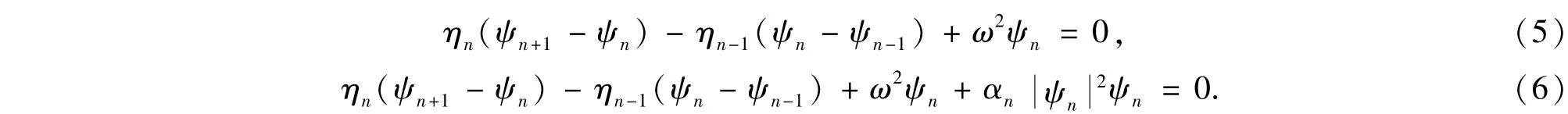
波在两端线性区域中满足平移对称性,可以用平面波表示,设波动从左端入射右端出射,则两端的波函数可以写成

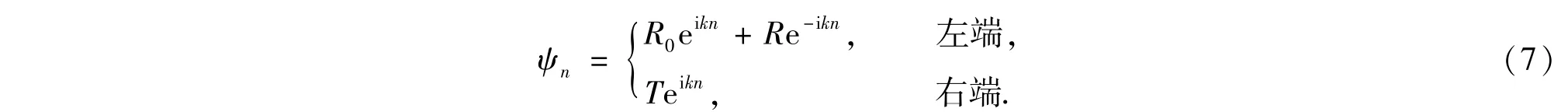
其中k为波矢,R0,R和T分别代表入射波振幅,反射波振幅和透射波振幅.由方程（5）和平面波函数（7）,可解出波动的色散关系为

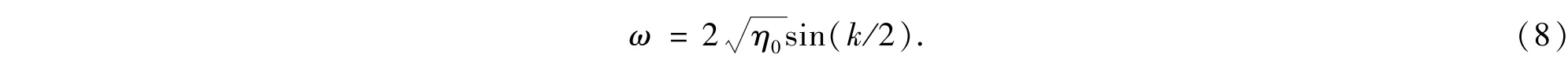
为简单起见,我们假设这两层非线性材料的厚度相同,且离散化的厚度恰好为一层的厚度.由方程（5）～（8）式可以得到透射率

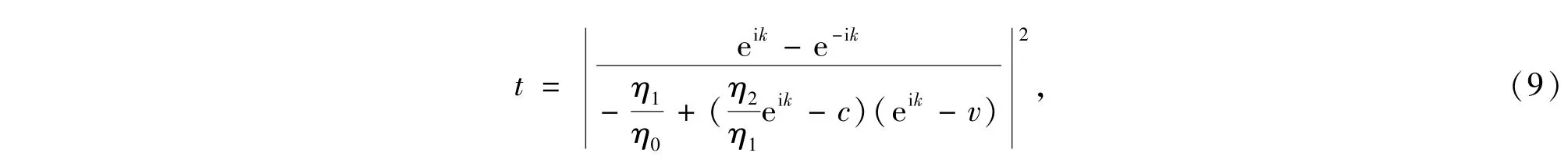
其中,

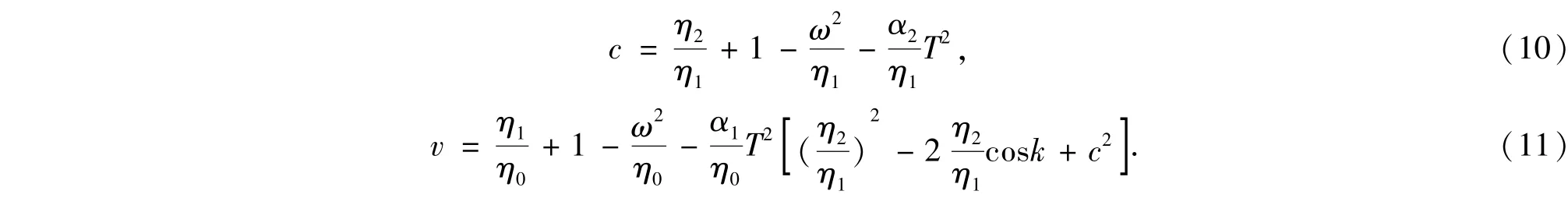
如果波动从右入射,从左出射,透射系数的表达式只需把式（9）～（11）式中的下标1、2对调即可.

2 结果和讨论

当η1＝η2,α1＝α2时,相同的波分别从系统的左端入射右端出射和从右端入射左端出射,从透射系数式（9）至（11）可以看出它们的透射率是相等的.在这种情况下不会出现二极管现象.若η1＝η2,α1≠α2,并引入因子m来表征非线性系数α的差异程度：m＝｜α1－α2｜/2.图2是在波矢k、介质刚度与平均密度的比值η、两层非线性介质的非线性强度的平均值α0都相同的情况下,非线性强度的差异m不同时,对应的透射系数随透射波振幅平方的变化（从左端入射,右端出射）.从图2可以看到介质层非线性强度不同时,在出射振幅为零的位置都存在一个透射率为1的透射峰；在出射振幅平方不为零的地方还出现一个峰,非线性强度的差异m愈大该透射峰的位置离原点就越远,且峰值也变小.因为方程（6）中的非线性项与波函数的振幅有关,当振幅趋于零时非线性相的作用消失,方程（6）回到线性方程（5）,所以在振幅趋于零时声波都能完全透射.当波函数振幅不为零时,非线性项会对透射起决定性的作用.

图2 透射率与透射振幅平方的关系（η1＝η2＝η0＝1）Fig.2 Dependence of transmission ratio on squaremodule of transmission amplitude（η1＝η2＝η0＝1）

从式（9）～（11）可以看到,我们求透射率时是用出射振幅当已知量,如果用入射振幅当初始条件,则必须由透射振幅通过方程反推入射振幅.设透射振幅为某一实数,但求出的入射振幅一般为复数.如果以入射振幅模方为自变量,则透射率随入射振幅模方的变化如图3所示.从图3中可以看出,当入射振幅模的平方取较小值时,透射率唯一与之对应.但当入射振幅模的平方取较大值时,会有两、三个不同的透射率与之对应,呈现多稳态现象.这是由非线性引起的[16－17].因此在后面讨论中我们用出射波振幅的平方作为透射率的自变量,而不用入射系数模的平方作为自变量.

当声波分别从两层非线性材料的左端和右端入射时,透射率t随透射振幅的平方T2和入射波波矢k的变化如图4、5所示.对照图4、5可以发现,非线性强度为相反数时,相当于波矢平移π.从图4、5中可以看出,相同的波从左端入射和从右端入射,其透射率是不相同的.这种分别从两端入射出现不同透射率的情况可以制造二极管,但必须是一端入射时透射率接近1,而从相反方向入射时透射率接近0.

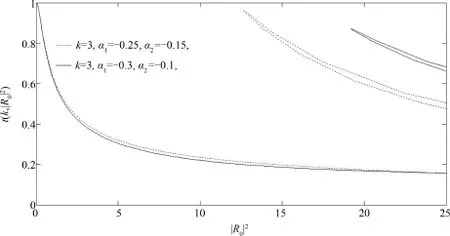
图3 透射率与入射振幅的关系（其它数据与图2相同）Fig.3 Dependence of transmission ratio on incident amplitude（Other parameters are the same as those in Fig.2.）

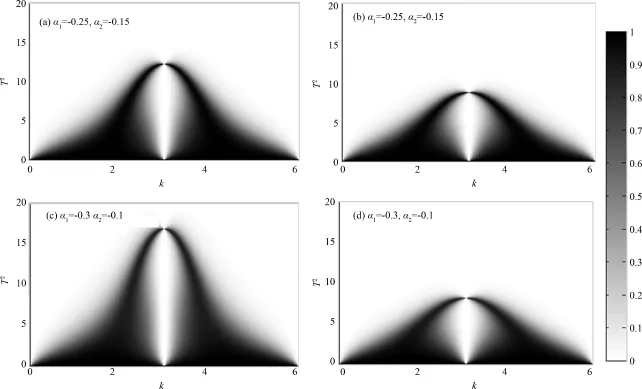
图4 透射率t随T2和入射波波矢k的变化,（a）和（c）声波从左端入射；（b）和（d）声波从右端入射（其它数据与图2相同）Fig.4 Dependence of transmission ratio t on T2and incidentwave vector k,（a）and（c）are for cases of left-incidence acoustic waves；（b）and（d）are for cases of right-incidence acoustic waves （Other parameters are the same as those in Fig.2.）

类似于光学中对比度的定义,引入整流因子

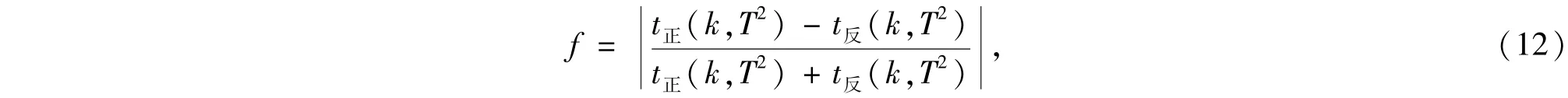
可以看出整流因子的范围为f∈[0,1],整流因子趋于1时,整流效果最佳.为了更清楚地看出在什么情形下整流效果比较好,我们作出了两层非线性材料的非线性系数平均值α0相同,非线性强度的差异m不同时的整流因子f随T2以及k的变化情况,如图6所示.从图中可以看出：在相同的情况下,非线性强度的差异m越大,整流效果越好.要得到好的整流效果,出射振幅平方要尽可能大.图6中的非线性强度的平均值相同,整流因子的分布情况比较接近；当整流因子的平均值远离0时,整流因子f接近0的白色部分向透射率平方小的方向急剧下降.因此,为得到好的整流效果,要求两层的非线性强度差异尽可能大,两者的平均值远离0值.

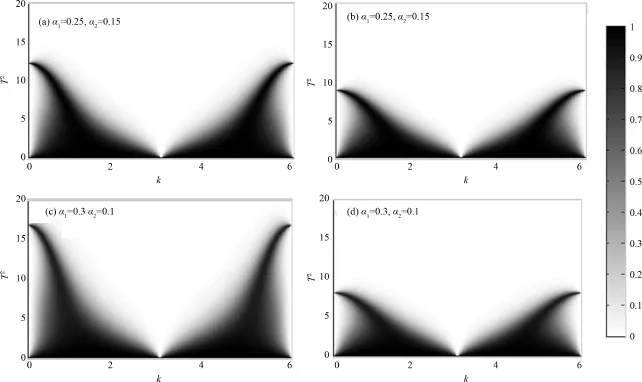
图5 透射率t随T2和入射波波矢k的变化,（a）和（c）声波从左端入射；（b）和（d）声波从右端入射（其它数据与图2相同）Fig.5 Dependence of transmission ratio t on T2and incidentwave vector k,（a）and（c）are for cases of left-incidence acoustic waves；（b）and（d）are the cases of right-incidence acoustic waves （Other parameters are the same as those in Fig.2.）

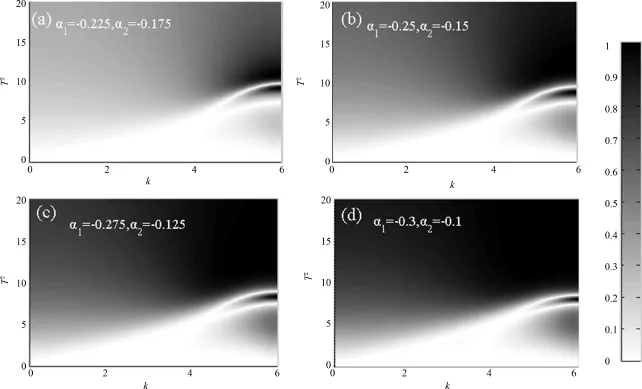
图6 整流因子f随T2以及k的变化（颜色的深浅用来表征f的大小.其它数据与图2相同.）Fig.6 Dependence of rectification factor f on T2and k（The shade of color represents degree of f.Other parameters are the same as those in Fig.2.）

3 结论

通过对声波在不同的双层非线性材料中正反向传播时的数值计算,我们发现在该系统中具有声二极管现象；随着非线性强度差异的增大,二极管效应愈明显.声波沿单向传播的声二极管的设计与实现,不仅具有学术意义,而且有望在未来新材料的应用中崭露头角.由于现有声二极管的透射率普遍偏低,在努力探索新的声二极管工作机理的同时,有必要通过寻找新材料或优化结构等手段来进一步提高声二极管样品的工作效率,最终制造出可应用的声二极管器件[18],我们的模型提供了实现声二极管的一种可能.

[1] Li BW,Wang L,CasatiG.Thermal diode：Rectification of heat flux[J].Physical Review Letters,2004,93（18）：184301－184304.

[2] Li BW,Lan JH,Wang L.Interface thermal resistance between dissimilar anharmonic lattices[J].Physical Review Letters, 2005,95：104302.

[3] Chang CW,Okawa D.Scolid-state thermal rectifier[J].Science,2006,314：1121.

[4] Kobayashi C,Teraoka Y,Terasaki I.An oxide thermal rectifier[J].Appl Phys Lett,2009,95：171905.

[5] Li BW,Wang J.Anomalous heat conduction and anomalous diffusion in one-dimensional systems[J].Phys Rev Lett,2003, 91：044301.

[6] Tao F,Chen W Z,Xu W.The unidirectional transmission of energy in the coupled transmission lines[J].Technical Acoustics,2011,30（6）：45－46.

[7] Scalora M,Dowling JP,Bowden CM.The photonic band edge optical diode[J].Journal of Applied Physics,1994,76（4）：2023－2026.

[8] Mingaleev SF,Kivshar Y S.Nonlinear transmission and light localization in photonic-crystal waveguides[J].Journal of Optical Society of America B,2002：19（9）：2241－2249.

[9] Lin Xusheng,Lan Sheng.Unidirectional transmission in asymmetrically confined photonic crystal defectswith Kerr nonlinearity [J].Chinese Phys Lett,2005,22（11）：2847－2850.

[10] Cai Xuhong,Lin Xusheng,Lan Sheng.Significant enhancement of unidirectional transmission in asymmetrically confined photonic crystal defect pairs[J].Chinese Phys Lett,2008,25（6）：2085－2088.

[11] Cho Y C.Reciprocity principle in duct acoustics[J].The Journal of the Acoustical Society of America,1980,67：1421.

[12] Narayan O,Dhar A.Nonreciprocity and the second law of thermodynamics：An exact relation for nonlinear media[J].Europhys Lett,2004,67（4）：559.

[13] Liang B,Yuan B,Cheng JC.Acoustic diode：Rectification of acoustic energy flux in one-dimensional systems[J].Phys Rev Lett,2009,103：104301.

[14] Liang B,Guo X S,Tu J,Zhang D,Cheng JC.An acoustic rectifier[J].Nature Materials,2010,9：989－992.

[15] Liu Qihai,Hu Dongsheng,Yin Xiaogang,et al.Defectmode in one-dimensional photonic crystal consisting of single-negative materialswith an impurity layer[J].Acta Phys Sin,2011,60（9）：094101.

[16] Delyon F,Levy Y E,Souillard B.Nonperturbative bistability in periodic nonlinearmedia[J].Phys Rev Lett,1986,57（16）：2010－2013.

[17] Hu Dongsheng,Zhang Yanling,Yin Xiaogang,et al.Transport properties of nonlinear chains with random dimer nonlinearity parameters[J].Acta Phys Sin,2012,61（17）：177103.

[18] Zou Xinye,Yuan Ying,Liang Bin,Cheng Jianchun.Acoustic one-way structures[J].Applied Acoustics,2013,32（3）：169 －181.

Diode Phenomenon of Acoustic W ave Propagation in a Two-Layer Nonlinear System

GUO Fengli1, HU Dongsheng1, XU Jiang2
（1.College of Science,Nanjing University of Aeronautics and Astronautics,Nanjing 211106,China；
2.Department ofMaterial Science and Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 211106,China）

In one-dimensional nonlinear system,linear parts of acoustic wave meet wave equation and nonlinear part is assumed similar to that of nonlinear Schrödinger equation.Transmission coefficients of two incident acoustic waves from opposite directions are calculated respectively.It is shown that this model has unidirectional penetrability for acoustic wave within certain frequency and amplitude,and expresses behaviors of diode.Increasing nonlinear intensity leads to a remarkable enhancement of unidirectional penetrability.

nonlinear system；acoustic wave；rectification；diode phenomenon

1001-246X（2015）06-0722-07

O422.7

A

2014－10－20；

2015－03－09

国家自然科学基金（11175086,51175245）及江苏省自然科学基金（BK2010073）资助项目

郭凤丽（1987－）,女,硕士,主要从事凝聚态物理研究