一种二次型忆阻器四阶混沌电路

余世成, 曾以成, 李志军（.湘潭大学光电工程系,湖南湘潭 405；.湘潭大学通信工程系,湖南湘潭 405）

一种二次型忆阻器四阶混沌电路

余世成1, 曾以成1, 李志军2
（1.湘潭大学光电工程系,湖南湘潭 411105；2.湘潭大学通信工程系,湖南湘潭 411105）

由HP实验室研制的无源忆阻器得到的荷控二次型忆阻器模型,与有源磁控分段线性和三次光滑忆阻器模型相比,更符合实际.利用此模型并基于蔡氏混沌电路演化而来的拓扑对偶结构设计了一种新型忆阻器四阶混沌电路.理论分析、仿真及电路实现表明,该电路具有依赖于忆阻器初始状态的复杂动力学行为,也会产生随时间和系统参数变化的状态转移等非线性动力学现象,在相轨图中出现“涡眼”和“环眼”.

二次型忆阻器；混沌电路；初始状态；状态转移

0 引言

忆阻器是继电阻、电容和电感之外的第四种基本双端电路元件,具有其它三种基本元件任意组合都不能替代的特性[1－2].忆阻器作为一个非线性元件,很容易产生混沌振荡信号,因此基于忆阻器的混沌电路研究备受关注[3－17].然而,忆阻器电路研究中普遍使用的忆阻器模型分别为分段线性（PWL）[3－6]和三次光滑型[7－8,14－15].二者皆为研究模型,研究人员只是用器件搭建了体现其特性的有源模型电路,并未在实际电路中实现相应模型的无源装置.我们利用HP实验室研制的无源忆阻器得到荷控二次型模型,研究基于忆阻器的四阶混沌电路,更具实际意义.因为是荷控型忆阻器,为了研究问题的方便采用由经典蔡氏电路转化而来的拓扑对偶电路,运用常规动力学研究方法[5,12,15－18]对该电路进行平衡点、稳定性等动力学特性分析.

此外,为电路实现需要构建模型的有源电路也是必要的.本文建立一种荷控二次型忆阻器有源模型电路,并在此基础上对混沌电路进行电路特性的验证研究.

1 二次型忆阻器四阶混沌电路及其理论分析

由文献[2]可以得到HP实验室研制的无源忆阻器阻值为

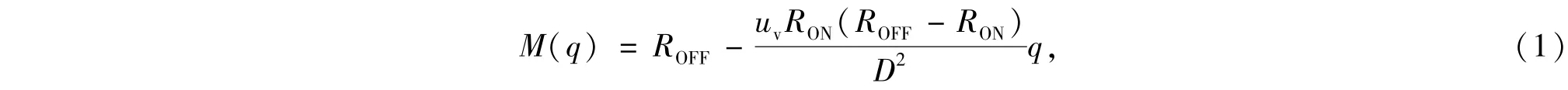
式中M（q）表示忆阻值,与电阻具有同一量纲；D是忆阻器总长度；uv是杂质平均移动速率；RON是导通阻抗；ROFF是关闭阻抗[2].等式右边除了通过忆阻器电荷q之外,其它量均为常量,故可简化为

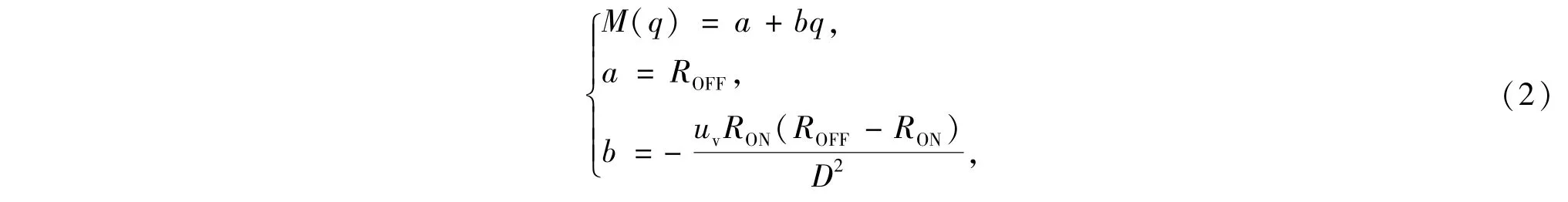
其中,a、b为常量,且有a＞0和b＜0.由（2）式和忆阻器的定义式可得HP实验室研制的无源忆阻器两端磁通和通过其电荷关系为

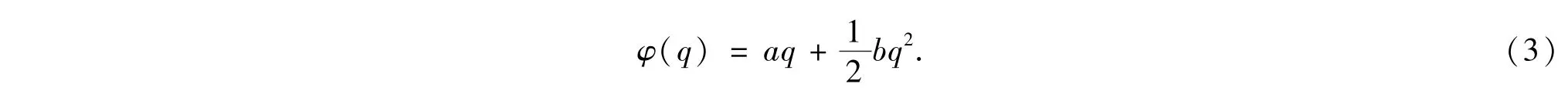
由（3）式可知忆阻器两端磁通是其电荷的二次函数,称该忆阻器模型为二次型的.由（2）式可知忆阻值M（q）为电荷的一次函数,因此该忆阻器模型为荷控二次型.

因为该忆阻器为荷控型忆阻器,若直接选用经典蔡氏电路进行非线性器件替换研究,忆阻值M（q）关于电荷q的表达式处于状态方程的分母,如图1（a）和方程组（4）所示,使问题的研究变得复杂.因此采用由经典蔡氏电路演化而来的拓扑对偶电路进行荷控二次型忆阻器混沌电路研究,如图1（b）和方程组（5）所示.

图1 荷控二次型忆阻器四阶混沌电路Fig.1 Change-control quadratic memristor-based fourth-order chaotic circuits

图1中（a）和（b）所示包含忆阻器电路的状态方程分别为

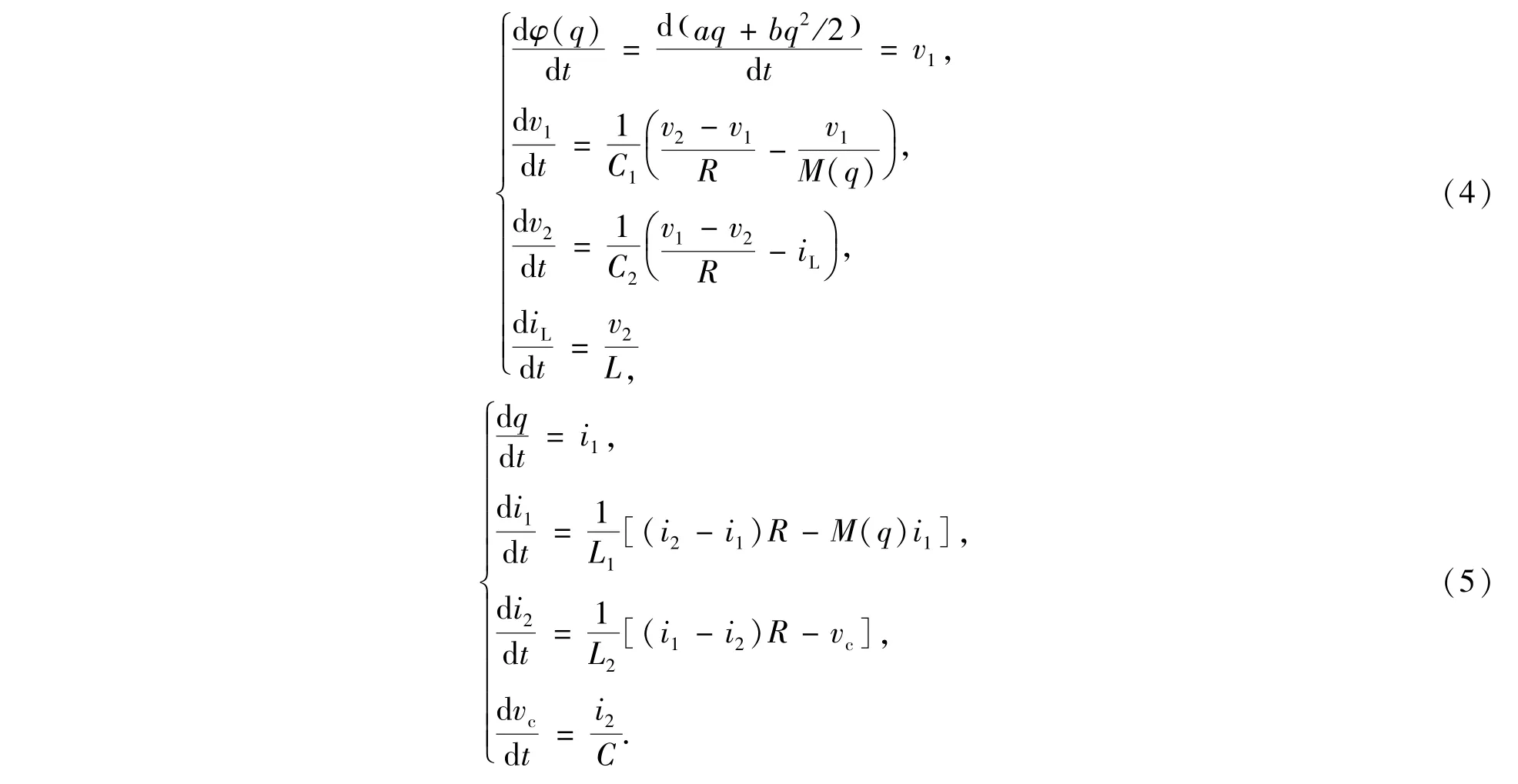
将（2）式代入方程组（5）,并令其各式等于零求解系统（5）的平衡点集合

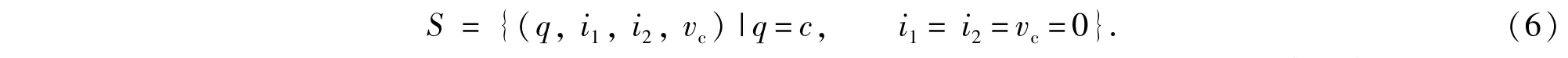
式中c是一个实常数,即系统（5）的平衡点为位于q坐标轴上的点集.为了方便研究简化参数使得α＝1/L1,β＝1/C,R＝1,L2＝1代入（5）式,并在平衡点线性化系统（5）得到Jacobi矩阵

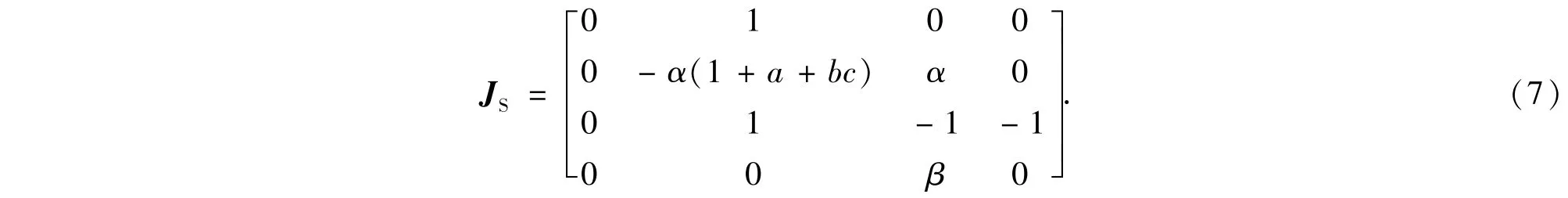
平衡点集S的特征根方程为

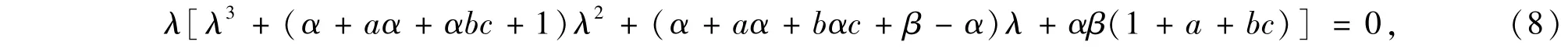
（8）式方括号中的三次多项式方程的系数均为非零实常数.根据Routh-Hurwitz稳定条件,该三次多项式方程根的实部为负的充分必要条件是：

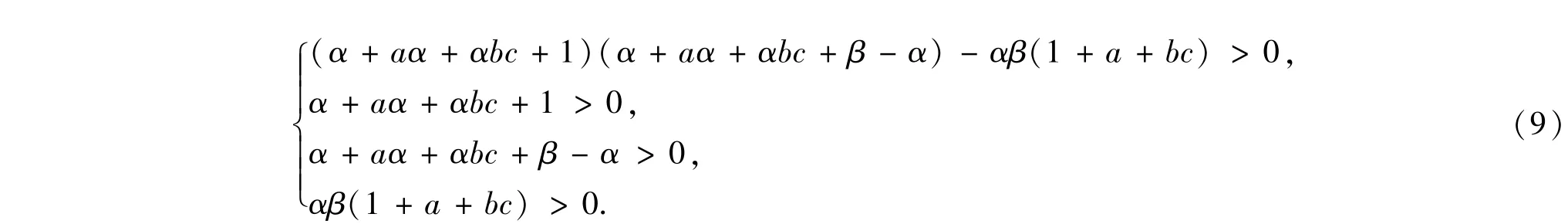
固定参数α＝7,β＝10,a＝1.5和b＝－1,选择c为可变参数代入（9）式可得平衡点集S稳定所对应的c值范围为

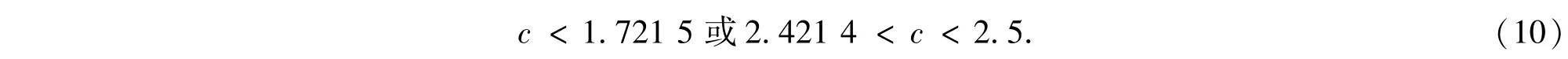
若忆阻器初始状态在q坐标上满足（10）式,其它坐标上初始值为零,则系统（5）从稳定平衡点集S出发的解是渐近稳定的,这时平衡点集S除零特征根之外的三个特征根的实部均为负.反之,可得平衡点集S不稳定所对应的c值范围为

由此点集出发系统（5）的解是不稳定的,轨迹趋于极限环、混沌轨或者无穷发散.

2 二次型忆阻器混沌电路动力学特性

在上节参数基础上,选取初始状态（q（0）,0,0.11,0）中q（0）为可变参数,利用Lyapunov指数谱和相轨图对图1（b）所示二次型忆阻器混沌电路进行动力学行为分析.系统（5）随初始值q（0）＝c变化和随时间演化的Lyapunov指数谱分别如图2（a）和图2（b）所示.为了图示清晰,图2（a）中Lyapunov指数曲线L4只画出了部分.根据李雅普诺夫指数与吸引子关系[5,8]和图2（a）数值仿真结果可知：当c＜1.702 1或2.358 4＜c ＜2.401 2时系统（5）的李氏指数均小于零,故此时系统是渐近稳定于不动点上；而当1.702 1＜c＜2.358 4 或c＞2.401 2时系统（5）的轨迹为极限环、混沌或发散.图2（a）数值仿真结果与式（10）和（11）范围有些许差别,该差异主要是系统（5）的平衡点集S除了三个非零特征根外还有一个零特征根所引起的.图2（b）为q （0）＝2.316 7时系统（5）随时间演化的Lyapunov指数谱,由图可知李氏指数L1大于零,即此时系统处于混沌态.

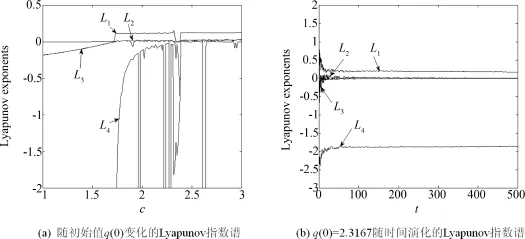
图2 随初始值q（0）变化和随时间演化的Lyapunov指数谱Fig.2 Lyapunov exponent spectrumswith variation of q（0）and time

选取初始状态变量q（0）几个典型常数值c＝1.65、1.722 1和2.316 7描绘系统（5）相应的相轨图,如图3所示.其中,图3（a）描绘c＝1.65时系统q-vc相轨图,此时系统轨迹是个汇点；图3（b）描绘c＝1.721 1时系统q-vc相轨图,此时系统轨迹是一周期极限环；图3（c）和（d）分别描绘c＝2.316 7时系统q-vc相轨图和三维图形,此时系统轨迹是单涡卷混沌轨.

若选取初始状态为（q（0）,0,10－10,0）,且初始值q（0）为c＝2.316 7、2.41时系统（5）的相轨图和相应的时序图如图4所示.其中,图4（a）描绘c＝2.316 7时系统q-vc相轨图和q-t时序图,此时系统出现了状态转移现象,由原来的平衡点状态趋向最终的混沌状态,在单涡卷之中出现了一个“涡眼”；图4（b）描绘c＝2.41时系统q-vc相轨图和q-t时序图,系统同样出现状态转移现象,由原来的平衡点状态趋近于最终的一周期状态,在极限环中出现一个“环眼”.

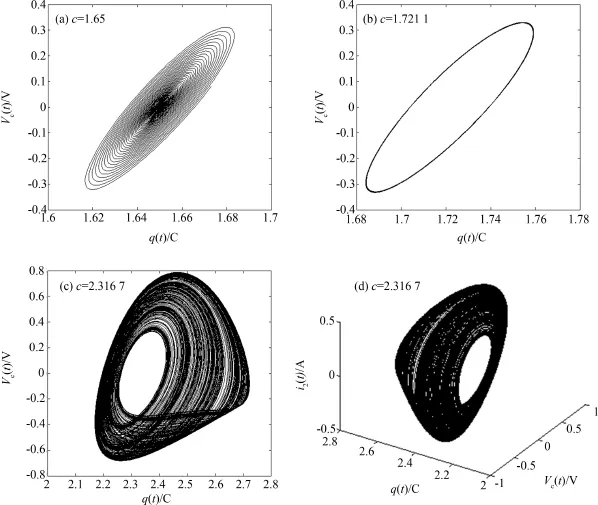
图3 不同初始值q（0）＝c下系统（5）的相轨图Fig.3 Phase diagrams of System（5）with different initial values q（0）＝c

此外,选取方程中的β为可变参数,初始状态为（2.316 7,0,0.11,0）,分析系统（5）随系统参数β变化的动力学行为.此时,系统（5）随参数β变化的分岔图如图5所示.由分岔图5可知,当β在区间[10, 15]连续变化时系统（5）经历了混沌态、周期态、稳定点几种状态变化,并且呈现出逆向倍周期分岔特性,几次倍周期分岔分别发生在β＝10.2、10.24和10.44.图5（b）是图5（a）局部放大图,其中β区间为[10.1,10.5].

图6为β在区间[10,15]连续变化时系统（5）的李雅普诺夫指数谱,由图可见系统（5）经历了混沌态、周期态、稳定点几种状态变化,进一步验证了图5呈现出的系统随参数β变化所发生的状态转移特性.同样, 图6（b）是图6（a）局部放大图,其中β区间为[10.1,10.5].

选取系统参数β几个典型常数值β＝10.15、10.25、12和14描绘系统（5）相应的相轨图,如图7所示.其中,图7（a）描绘β＝10.15时系统q-i2相轨图,此时系统轨迹是单涡卷混沌轨；图7（b）描绘β＝10.25时系统q-i2相轨图,此时系统轨迹是二周期极限环；图7（c）描绘β＝12时系统q-i2相轨图,此时系统轨迹是一周期极限环；图7（d）描绘β＝14时系统q-i2相轨图,此时系统轨迹是个汇点.

图8描绘系统（5）在不同状态（β＝10.15和10.25）下且截平面为i1＝0.35时系统庞加莱截面图,根据系统状态和庞加莱截面图关系[19]可知：图8（a）所示曲线图映射出系统此时处于混沌状态,恰好与图7（a）描绘的系统状态相对应；图8（b）所示离散点图映射出系统此时处于二周期状态,与图7（b）描绘的系统状态相对应.

综上,由图3可知二次型忆阻器混沌系统（5）产生了随初始状态变化的状态转移非线性动力学现象；由图4可知二次型忆阻器混沌系统（5）产生了随时间变化的状态转移现象；由图7可知二次型忆阻器混沌系统（5）产生了随系统参数变化的状态转移.同时,由图5可知随参数β变化系统（5）处于混沌态区间大致为[10,10.18],处于倍周期分岔区间大致为[10.18,10.45],因此系统（5）在[10,10.45]区间段内对参数的微小变化有较强的敏感性.由此可见,同分段线性（PWL）[3－4]和三次光滑型[8,15]忆阻器混沌电路一样,二次型忆阻器混沌电路具有与一般混沌系统不同的复杂动力学行为.

图4 初始状态为（q（0）,0,10－10,0）时系统（5）的相轨图和时序图Fig.4 Phase diagrams and sequence charts of System（5）with initial stare（q（0）,0,10－10,0）

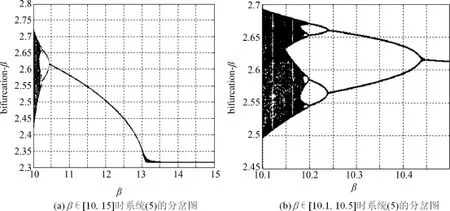
图5 系统（5）随参数β变化的分岔图Fig.5 Bifurcation diagrams of System（5）with variation of parameterβ

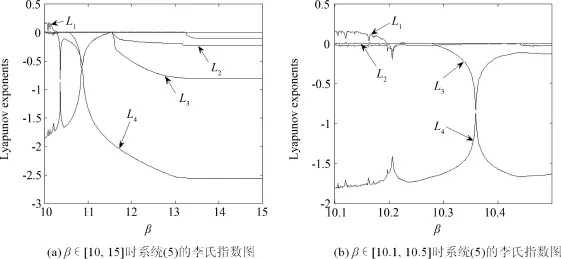
图6 系统（5）随参数β变化的李氏指数谱Fig.6 Lyapunov exponent spectrums with variation of parameterβof System（5）

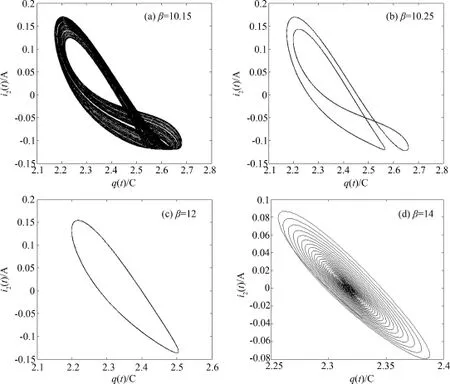
图7 不同参数β下系统（5）的相轨图Fig.7 Phase diagrams of System（5）with different parameterβ

3 二次型忆阻器有源模型电路实现与混沌电路特性验证

由于HP实验室研制的无源忆阻器还未实现商业化生产,因此搭建其有源模型电路进行进一步研究验证是很有必要的,一种二次型忆阻器有源模型电路构建如图9所示.

图9激励源Vin以右部分电路即可等效为一个二次型忆阻器,该有源模型电路使用了电流反馈运算放大器AD844和乘法器AD633,并有C1＝C2,VH＝＋15V,VL＝－15 V.电流反馈运算放大器AD844的电路特性为

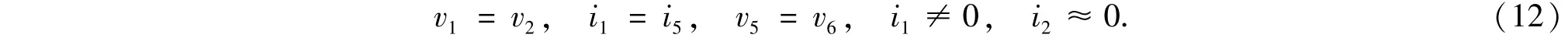
乘法器AD633的电路特性为

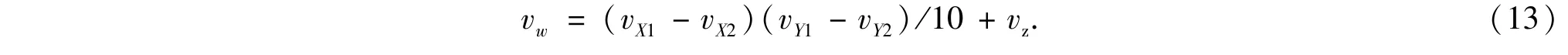
图8 在不同状态下系统（5）庞加莱截面图Fig.8 Poincare sections of System（5）with different system states

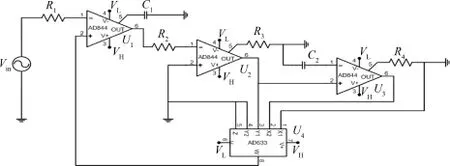
图9 二次型忆阻器有源模型电路Fig.9 An activemodel circuit of quadratic memristor

由（12）式和（13）式以及器件连接关系得图9所示有源等效电路表达式为

比较（14）式和（2）式可知该有源模型电路满足荷控二次型忆阻器忆阻值与电荷之间的特性关系,实现了电路等效.当激励源Vin为正弦信号,该忆阻器等效模型i-v特性如图10所示,其中各器件参数值为：R1＝16 kΩ,R2＝3 kΩ,R3＝6 kΩ,R4＝10 kΩ,C1＝C2＝100 nF.图10（a）是激励源Vin频率为200 Hz时忆阻器等效模型i-v曲线,曲线形状为斜八字型；图10（b）是激励源Vin频率为2 kHz时等效模型i-v曲线,此时曲线退化为一条过原点直线.因此,电路仿真结果表明该二次型忆阻器有源模型电路特性符合文献[2]描述的HP实验室研制的无源忆阻器电路特性.

基于该有源模型电路的二次型忆阻器四阶混沌电路如图11所示,使用运算放大器AD711是为了实现负阻－R[5,8,13],其中相应器件参数值为：R＝2.1 kΩ,R5＝R6＝2 kΩ,L1＝9 mH,L2＝63 mH,C3＝6.3 nF.

式（14）表明通过忆阻器的电荷q可由电容C1两端的电压vc1表示,因而电路初始状态的电荷值q（0）即由电容C1初始时刻的电压值IC（C1）体现.选取初始状态（IC（C1）,0,11×10－8,0）,此时基于二次型忆阻器有源模型混沌电路在不同初始值IC（C1）下电路特性如图12所示.图12（a）是IC（C1）＝1.42 V时,电路中电容C1和电容C3上电压关系图,也即是系统（5）的q-vc相轨关系图,此时系统轨迹是一周期极限环；图12（b）是IC（C1）＝1.55 V时,二者电压关系图,此时系统轨迹是单涡卷混沌轨.由此可知二次型忆阻器有源模型混沌电路随初始状态变化发生了状态转移,对电路初值有较强的敏感性.

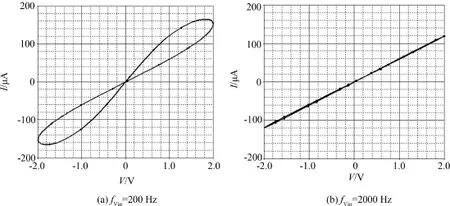
图10 二次型忆阻器有源模型在不同频率下i-v特性Fig.10 Characteristic i-v of activemodel circuit at different frequencies

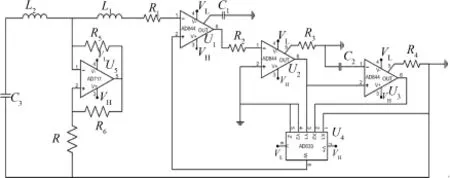
图11 基于二次型忆阻器有源模型的四阶混沌电路Fig.11 A fourth-order chaotic circuit based on activemodel circuit

图12 基于忆阻器有源模型混沌电路在不同初始值IC（C1）下电路特性Fig.12 Circuit characteristics of chaotic circuitwith different initial values IC（C1）

4 总结

从HP实验室研制的无源忆阻器出发,推导出其荷控二次型忆阻器模型.在此基础上,研究了基于此模型的忆阻器四阶混沌电路,为了方便问题的研究采用经典蔡氏电路演化而来的拓扑对偶电路,使用常规动力学研究方法对其特性进行了相应的理论分析和数值仿真,结果表明：荷控二次型忆阻器四阶混沌电路具有随初始状态、时间和系统参数变化而发生状态转移的复杂非线性动力学行为,相轨图中出现“涡眼”和“环眼”,对电路初值和系统参数有较强的依赖性和敏感性.同时,构建一种荷控二次型有源模型电路对其混沌电路特性做进一步验证.此外,与忆阻器混沌振荡电路研究中普遍使用的分段线性（PWL）和三次光滑型忆阻器模型相比,研究基于荷控二次型忆阻器混沌电路,由于该模型无源器件的存在而更具实际意义.

[1] Chua L O.Memristor—Themissing circuit element[J].IEEE Transactions on Circuit Theory,1971,18（5）：507－519.

[2] Strukov D B,Snider G S,Stewart D R,Williams R S.Themissingmemristor found[J].Nature,2008,453（6932）：80－83.

[3] Lin Z,Wang H.Efficient image encryption using chaos-based PWLmemristor[J].IETE Technical Review,2010,127（4）：318－343.

[4] Wen SP,Shen Y.Chaos analysis and control in chaotic circuitwith a PWLmemristor[J].IEEE Transactions on Information Science and Technology,2011,2（11）：1030－1033.

[5] Li Z J,Zeng Y C.A memristor oscillator based on a twin-T network[J].Chinese Phys B,2013,22（4）：040502.

[6] Zhong Q S,Yu Y B,Yu JB.Fuzzymodeling and impulsive control of amemristor-based chaotic system[J].Chinese Physics Letters,2010,27（2）：020501.

[7] Buscarino A,Fortuna L,Frasca M,Gambuzza L V.A gallery of chaotic oscillators based on HPmemristor[J].International Journal of Bifurcation and Chaos,2013,23（5）：14.

[8] Muthuswamy B.Implementingmemristor based chaotic circuits[J].International Journal of Bifurcation and Chaos,2010,20 （5）：1335－1350.

[9] Querlioz D,Bichler O,Gamrat C.Simulation of amem ristor-based spiking neural network immune to device variations[C]∥Neural Networks（IJCNN）,The 2011 International Joint Conference on IEEE,2011：1775－1781.

[10] Yakopcic C,Taha TM,Subramanyam G,et al.A memristor device model[J].IEEE Electron Device Letters,2011,32 （10）：1436－1438.

[11] Tian X B,Xu H,LiQ J.The conductivemechanisms of a titanium oxidemem ristorwith dopant driftand a tunnel barrier[J].Chinese Phys B,2013,22（8）：088502.

[12] Wen S,Zeng Z,Huang T.Fuzzymodeling and synchronization of differentmemristor-based chaotic circuits[J].Phys Lett A, 2013,377（34）：2016－2021.

[13] Bao B C,Xu J P.Chaotic memristive circuit：Equivalent circuit realization and dynamical analysis[J].Chinese Physics Letters,2011,20（12）：120502.

[14] 胡丰伟,包伯成,武花干,王春丽.荷控忆阻器等效电路分析模型及其电路特性研究[J].物理学报,2013,62（21）：218401.

[15] 包伯成,史国栋,许建平.含两个忆阻器混沌电路的动力学分析[J].中国科学：技术科学,2011,41（8）：1135－1142.

[16] 李志军,曾以成.基于文氏振荡器的忆阻混沌电路[J].电子与信息学报,2014,34（1）：88－93.

[17] 李志军,曾以成,李志斌.改进型细胞神经网络实现的忆阻器混沌电路[J].物理学报,2014,63（1）：010502.

[18] 王梦蛟,曾以成,徐茂林.一类自治混沌系统的动力学分析与电路实现[J].计算物理,2010,27（6）：927－932.

[19] 陈红,吴玲.设计和实现三维空间任意庞加莱截平面电路[J].物理学报,2013,62（2）：020507.

A Quadratic M em ristor-based Fourth-order Chaotic Circuit

YU Shicheng1,ZENG Yicheng1,LIZhijun2
（1.Department ofOptoelectronic Engineering,Xiangtan University,Xiangtan Hunan 411105,China；
2.Department ofCommunication Engineering,Xiangtan University,Xiangtan Hunan 411105,China）

Compared with active piecewise linear（PWL）and cubic smoothmemristormodel adopted inmostmemristor-based chaotic circuits,charge-control quadratic memristormodel ismore practical,which is derived from a passive device fabricated by HP Labs.Based on the model and a topological dual structure of Chua’s chaotic circuit,a memristor-based fourth-order chaotic circuit was designed.As is verified by theoretical analysis,simulation and circuit realizations,the charge-control quadratic memristor-based chaotic circuit has complex dynamical behaviors relying on initial state ofmemristor.Meanwhile,non-linear dynamical phenomenon of state transition is generated along with variation of initial state,time and system parameters.An eye of scroll and an eye of limit cycle are observed in phase diagrams of chaotic circuits.

quadratic memristor；chaotic circuit；initial state；state transition

1001-246X（2015）06-0735-09

O415.5

A

2013－12－20；

2014－07－14

国家自然科学（61176032,61233010）资助项目

余世成（1989－）,男,汉族,福建南平,硕士研究生,研究方向：基于忆阻器的混沌电路应用于信号检测, E-mail：shichengyu＠126.com