基于格子Boltzmann方法的平板射流大涡模拟

上官燕琴, 王 娴通讯作者：王娴（1977－）,女,汉族,吉林,副教授,博士生导师,主要研究方向：基于CPU/GPU体系的大规模并行计算、湍流的数值模拟、两相流的数值模拟,E-mail：wangxian＠mail.xjtu.edu.cn, 李跃明（西安交通大学航天航空学院机械结构强度与振动国家重点实验室,西安碑林 710049）

基于格子Boltzmann方法的平板射流大涡模拟

上官燕琴, 王 娴∗∗通讯作者：王娴（1977－）,女,汉族,吉林,副教授,博士生导师,主要研究方向：基于CPU/GPU体系的大规模并行计算、湍流的数值模拟、两相流的数值模拟,E-mail：wangxian＠mail.xjtu.edu.cn, 李跃明
（西安交通大学航天航空学院机械结构强度与振动国家重点实验室,西安碑林 710049）

应用多GPU技术,将格子Boltzmann方法与大涡模拟相结合（LBM-LES）,使用1.12×108网格,对雷诺数Re＝4 000,倾斜角α＝30°,吹风比M＝0.5工况下的平板单孔射流进行了大规模高性能数值模拟研究.合理的定性与定量结果验证了LBM-LES模拟平板射流的有效性与可行性.使用上亿的计算网格捕捉了精细的湍流拟序结构,有利于主流与射流之间的掺混机理研究.此外,使用6个K20M GPU并行计算,模拟了71 680 LBM时间步长,仅耗时15 402秒,计算性能达到521.24MLUPS,即每秒更新5.212 4×108个网格点的数据.

格子Boltzmann方法（LBM）；大涡模拟（LES）；多GPU；三维平板射流（JICF）

0 引言

平板射流（JICF）是工程中极其常见的一种流动模型,也是一种高度复杂的湍流流动.虽然它的边界条件很简单,但可作为众多具有重要工程价值的复杂流动的简化模型,例如：烟缕扩散,燃烧器的燃油喷射以及涡轮燃气发动机叶片的气膜冷却等[1].因此研究平板射流的流动并分析主流与射流之间的掺混机理,在实际工程应用中有着十分重要的意义.迄今为止,已有很多关于平板射流的实验研究与数值研究结果,但由于其流动情况的复杂性以及实验与数值方法的局限性,至今对于平板射流的掺混机理的认知程度还极其有限.为了得到更精确的平板射流数值结果,我们尝试应用格子Boltzmann方法（LBM）结合多GPU并行技术,使用上亿网格计算平板射流的流动.

LBM是近三十年来兴起的一种新的计算流体力学数值模拟方法.由于它具有天然的并行性、适于处理复杂几何边界问题和容易编程等优点[2],已逐渐形成一项引人注目的数值模拟技术.目前,LBM已在计算流体力学领域取得了很大的成功,它在常规流场的模拟,多孔介质,多相流,多组分流以及电磁流等领域有着很广泛的应用前景[3],但其在模拟湍流的可行性与正确性方面还有待进一步验证[4－5].

平板射流是高度复杂的湍流流动,湍流模型的选取对其计算精度的影响很大.目前关于平板射流的数值研究大部分都是基于雷诺平均方程（RANS）的,但Acharya等人已证明RANS结合湍流模型无法很好地捕捉平板射流中的流动动态从而使其过小地预测了气膜冷却中温度场的侧向传热[6].随后Tyagi等人首次尝试使用大涡模拟（LES）计算平板射流,并得到了精确的计算结果[7].之后越来越多的研究人员开始使用LES模拟平板射流及气膜冷却并得到了精确的结果[8－10].本文将LES与LBM相结合用于平板射流的数值研究.

大量的计算资源耗费是当前湍流精确计算的瓶颈之一,可编程GPU（GPGPU）的出现在一定程度上解决了这个瓶颈问题.现在,GPGPU已发展成为一种高度并行化、多线程、多核、多种编程接口的处理器[11],这样仅需在普通的个人计算机上安装一个或多个GPU接口单元便可完成大规模的并行计算,大大方便了计算流体力学工作者进行相关工作.这也使得结合多GPU并行技术完成高精度湍流数值模拟成为一种可能和趋势.

本文的主要工作是：基于LBM-LES并结合多GPU并行技术使用上亿网格计算三维平板射流的流动,得到高度复杂湍流流场的精细拟序结构,分析其掺混机理.

1 数值计算方法

1.1 格子Boltzmann方程

在LBM中,首先,将Boltzmann方程在分离的网格点中离散成速度分布[12]

其中,fi是离散点的速度分布函数,ei是离散点第i方向的速度,与此同时,N是每个离散点所含速度方向的总数.常见模型有：D2Q9,D3Q13,D3Q15,D3Q19,D3Q27.上式中的Ωi是碰撞项,用Boltzmann-BGK近似[13]可以得到

将其代入式（1）,得到

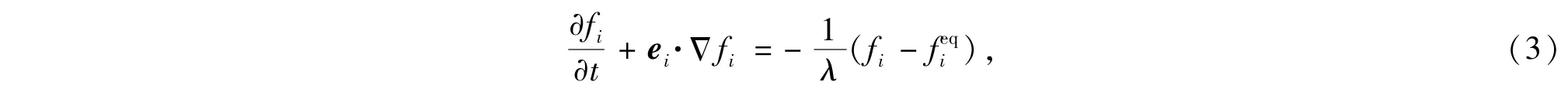
其中,feqi是平衡分布函数,λ是松弛时间.

为了得到准确的计算结果,合适的平衡分布函数的选取是很重要的,本文选用的平衡分布函数

本文使用D3Q19模型,其速度分布为：e0（0,0,0）,e1（1,0,0）,e2（－1,0,0）,e3（0,1,0）,e4（0,－1,0）, e5（0,0,1）,e6（0,0,－1）,e7（1,1,0）,e8（－1,1,0）,e9（1,－1,0）,e10（－1,－1,0）,e11（1,0,1）,e12（－1,0, 1）,e13（1,0,－1）,e14（－1,0,－1）,e15（0,1,1）,e16（0,－1,1）,e17（0,1,－1）,e18（0,－1,－1）.

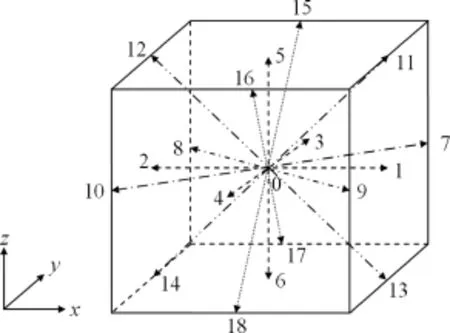
图1 D3Q19模型Fig.1 D3Q19 LBM model

声速为cs＝1/3,与此同时,对于理想气体而言,其压强为

进一步在空间x方向和时间t上离散方程（3）,可以得到它的完全离散形式

式（8）就是著名的LBGK模型.其中,τ＝λ/δt是无量纲的松弛时间.粘性υ可以从上式中推导得到

一般情况下,假设δt＝1,式（8）可以演化成以下两个基本步骤碰撞步：

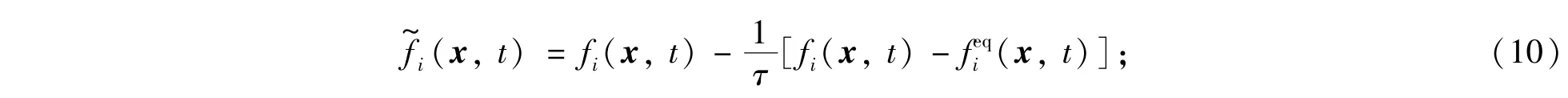
迁移步：

其中,fi和分别表示碰撞前与碰撞后的分数.

1.2 大涡模拟：Smagorinsky亚格子应力模型

大涡模拟（LES）的基本思想是通过对控制方程滤波,以实现波的大小尺度分离,再直接求解大尺度的涡旋,对于小空间尺度的涡旋则利用亚格子应力模型进行求解[14].Smagorinsky亚格子应力模型是常用的一种模型,该模型假设雷诺应力仅依赖于局部的应变率.

经过滤波之后的格子Boltzmann方程[4,15－16]变成

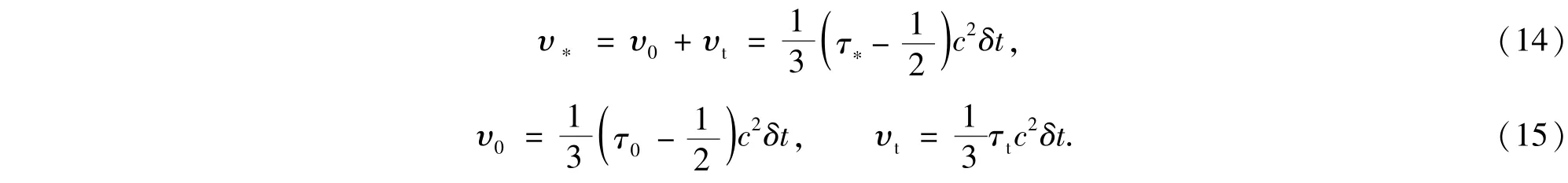
在标准Smagorinsky模型中,涡粘性υt可以通过滤波长度尺度Δx和过滤后的应变率张量＝（＋）/2计算得到

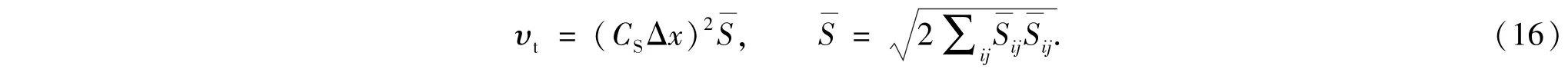
式（16）中的CS是Smagorinsky系数.本文参照作者之前基于LBM-LES的壁面约束流动数值模拟[17],取CS＝0.13.此外,本文选择了有限差分方法计算应变率张量.

2 计算模型

图2为本文计算模型.其中,x、y、z分别表示流向、展向与垂向,对应方向的计算区域长度为Lx、Ly与Lz.计算网格数Lx×Ly×Lz＝896×320×390,总网格数约为1.12×108.射流孔孔径D为平板展向长度的1/8,即D＝Ly/8.射流孔中心即为坐标原点,且射流孔中心位于主流出口下游5D的Ly/2平面上.u∞为自由来流速度,uj为射流速度.吹风比被定义为M＝ρjuj/ρ∞u∞（假设主流密度与射流密度相同）,其中,射流出口是均匀出口速度分布,uj是射流在冷却孔出口界面内的平均速度.射流速度方向相对于主流速度方向的倾斜角度为α.雷诺数定义为Re＝ρu∞D/υ,υ为运动粘性系数.本次计算工况设定为：Re＝4 000,α＝30°,M＝0.5.

图2 计算模型Fig.2 Flow configuration

边界条件的设置为：主流入口和射流入口均采用入口速度边界条件,平板为无滑移壁面,主流出口采用对流出口边界条件,展向前后边界为周期性边界条件,上边界采用充分发展边界条件.

3 结果与讨论

3.1 多GPU的计算性能

计算网格设置为896×320×390,总计算网格量达到1.12×108.计算的工况：雷诺数Re＝4 000,射流倾斜角α＝30°,吹风比M＝0.5.本文采用了6个K20M GPU并行计算,应用CUDA-MPI进行数据传输[18－19],模拟了7.168×104LBM时间步长,耗时15 402秒,计算性能达到521.24 MLUPS.

3.2 湍流的拟序结构

经过一个多世纪的研究表明：湍流是多尺度有结构的不规则流体运动.也就是说,湍流并不是完全的不规则运动,其多尺度不规则的运动中存在着可辨识的、有明确统计周期与外形的流动结构——拟序结构.这种拟序运动主宰着湍流的脉动生成与发展,因此拟序结构对流场的混合以及流体的扩散等起着重要作用[20－21].所以,平板射流流场中拟序结构的精细捕捉与分析有助于研究主流－射流掺混机理.

图3是选用Q判据作为漩涡识别方法[22]得到的1.792×104LBM时间步长的瞬态湍流拟序结构.在该图中可以清晰地看到平板射流流场中的典型拟序结构：位于射流前缘的马蹄涡,位于射流孔之后的发卡涡以及剪切层涡.

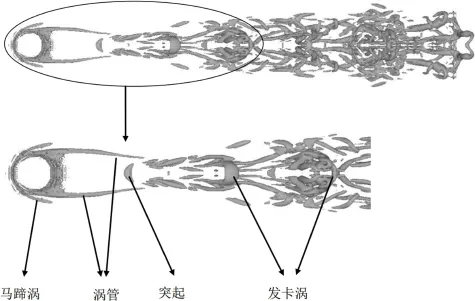
图3 1.792×104LBM步长的瞬态湍流拟序结构Fig.3 Instantaneous coherent structures at1.792×104LBM-steps

从拟序结构图上可以看到,射流从斜圆孔射出后立即就形成一些初级结构,然后开始向下游移动并形成一系列的发卡涡.这与Tyagi等在文献[7]中对平板射流的近壁处边界层的研究讨论相一致.而且在射流上风面附近区域有几段较短的涡管.射流与主流横向速度之间的相互作用是形成涡管的原因.这些涡管从射流孔周围产生后沿着主流流向弯曲,并附着于发卡涡上方.由于此算例中射流与主流的横向速度之间的相互作用比较弱,所以涡管产生之后,断断续续地附着在发卡涡上方.图3给出的合理的湍流拟序结构图说明了LBM-LES模拟平板射流的有效性与可行性.

图4显示的是在相同计算工况下由不同网格量计算得到的同一时刻（1.792×104LBM时间步长）的湍流拟序结构.图4（a）显示的是使用本文的计算网格设置计算得到的结果,总网格量为1.12×108.图4（b）则是由512×200×256的计算网格设置计算得到的结果,总网格量为2.62×107,前者使用的网格量约是后者的4.27倍.由对比结果可以明显看到：当使用的计算网格规模达到108,可以精细地捕捉到二级涡结构甚至是三级涡结构；而使用的计算网格规模为107时,只能够得到清晰的一级涡结构.

3.3 二次流动特性分析

图5显示在y＝Ly/2平面的1.792×104LBM步长瞬态相对压力云图,其中定义相对压力为：P＝（p－p∞）/ρu∞.从该图上我们可以清楚地看到射流射出之后就在射流孔后缘出现了一个较强的低压区,之后也出现了几个低压区,随着位置的后移,其强度变弱.这些低压区其实是反对称涡生成的区域,其强度也对应代表了反对称涡的强度.反对称涡是在垂直于流动方向的平面生成的,属于二次流动,其对射流与主流之间的掺混起主要作用.由该结果可以看到,反对称涡在射流孔中心位置开始产生,然后沿着流向移动,但强度逐渐减弱.

图4 不同计算网格规模下同一瞬态时刻（1.792×104LBM时间步长）湍流拟序结构对比图Fig.4 Instant（1.792×104LBM steps）coherent structures computed with different grids

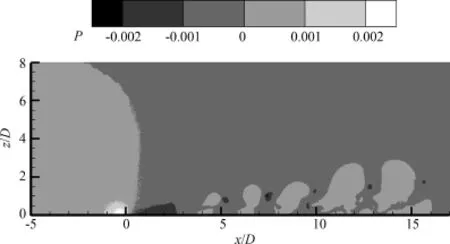
图5 y＝Ly/2平面的1.792×104LBM步长瞬态相对压力云图Fig.5 Instantaneous pressure contours above the bottom plate in plane of y＝Ly/2 at 1.792×104LBM-steps

在图6中可以看到分别位于斜圆孔下游0倍直径即圆孔中心位置（图6（a））、1倍直径（图6（b））、3倍直径（图6（c））、5倍直径（图6（d））、7倍直径（图6（e））以及9倍直径（图6（f））处的垂直于平板的纵剖面的1.792×104LBM步长瞬态流线图和涡量云图.由该结果可以看到,在射流孔中心位置上已经开始形成反对称涡,这与图5显示的在射流孔中心位置后即刻出现的强低压区相一致.而且,与其它不同位置的涡量相比,该处的涡量值是最大的,也就说明这是的反对称涡的强度是最大的.反对称涡是由主流与射流之间的剪切效应而产生的,使主流被射流夹带到射流下方.而由图6可以看到,距离射流孔越远,反对称涡涡强度越小.这也与由图5得到的结论相一致.而且随着与射流孔的距离越来越大,反对称涡的尺寸也越来越大,然而流向位置为x/D＝5.0是一个转折点,在x/D＝5.0之后反对称涡的强度与尺寸都随着与射流孔的距离的变大而变小.这是因为在x/D/5.0以及之后的位置已经位于耗散区内,湍流耗散在该区域占主导作用.也就意味着在耗散区主流与射流之间由于速度差而产生的剪切效应逐渐因湍流耗散而消失.

3.4 平均速度与定量比较

为了更好地说明本文使用的计算程序的准确性,我们参照了Özcan和Larsen等人完成的平板射流实验[23－24],定量地比较了计算结果.该实验测量的工况是：雷诺数Re＝2 400,倾斜角α＝90°,吹风比为M＝3.31.我们计算得到y＝Ly/2平面上不同流向位置的平均速度结果并与试验结果比较.

图6 不同流向位置的垂直于平板的纵剖面的1.792×104LBM步长瞬态流线图和涡量云图Fig.6 Contours of instantaneous vorticity component in streamwise directionωxand streamlines onvarious cross sections along streamwise direction at1.792×104LBM-steps

图7展示了y＝Ly/2平面上不同流向位置（a）和（c）x/D＝－0.5和（b）和（d）x/D＝0.5的平均流向速度以及平均垂向速度,其中实线代表的是LBM-LES的计算结果,而实心三角形代表的是实验结果[23－24].为了便于定量结果的比较,图7中显示的均是无量纲结果,其中平均速度使用主流速度u∞进行无量纲化,而垂向距离使用孔径D进行无量纲化.由图7可以清楚地看到：除了邻近壁面区域（z/D＜2.0）计算结果与实验结果之间有较大偏差外,其余区域的计算结果与实验结果均可较好地吻合.该图从定量上说明了使用LBMLES可以准确地计算平板射流这种复杂的流动情况.

在射流孔出口前缘位置（x/D＝－0.5）,流向速度u与垂向速度w除了z/D＜0.5的区域以外,其余区域均还保持着原本的主流速度分布情况,这是由于在射流孔前缘上主流与射流还未开始掺混,所以射流对主流速度分布的影响区域极小.在出口后缘即x/D＝0.5位置上,流向速度u在近壁面区域为负值,这是因为当射流从出口喷射出来后,在后缘位置产生了“回流”现象.

4 结论

应用多GPU技术,将格子Boltzmann方法与大涡模拟相结合（LBM-LES）,采用D3Q19单松弛时间模型,使用了1.12×108计算网格,得到并分析了雷诺数Re＝4 000,倾斜角α＝30°,吹风比为M＝0.5情况下三维平板单孔射流的精细的湍流拟序结构和不同流向位置的二次流动结果,定性地说明了LBM-LES模拟平板射流这种复杂流动情况的合理性.与此同时,参照Özcan和Larsen等人完成的横向射流实验[23－24],其实验工况为：雷诺数Re＝2 400,倾斜角α＝90°,吹风比为M＝3.31.比较了y＝Ly/2平面上不同流向位置的平均速度,合理的计算结果定量地说明了LBM-LES可以准确地计算平板射流.

多GPU技术的应用,使计算性能得到了显著的提高,使得上亿网格的湍流非稳态计算在数小时之内即可完成,有效地解决了高精度湍流数值模拟研究发展的瓶颈问题之一：计算消耗大.使用上亿的计算网格量不仅能够捕捉到精确的初级拟序涡结构,还可以得到精细的次级拟序涡结构,有助于主流与射流之间掺混机理的研究.

图7 y＝Ly/2平面上不同流向位置Fig.7 Profiles ofmean streamwise（a）and（b）and wall-normal（c）and（d）velocity components in plane of y＝Ly/2 at locations near jet exit x/D＝－0.5 and x/D＝0.5

[1] Bogard D G,Thole K A.Gas turbine film cooling[J].Journal of Propulsion and Power,2006,22（2）：249－270.

[2] 何雅玲,王勇,李庆.格子Boltzmann方法的理论及应用[M].北京：科学出版社,2009.

[3] Chen SY,Doolen G D.Lattice Boltzmannmethod for fluid flows[J].Annual Review of Fluid Mechanics,1998,30：329－364.

[4] Yu H,Girimaji S S,Luo L S.DNS and LES of decaying isotropic turbulence with and without frame rotation using lattice Boltzmann method[J].Journal of Computational Physics,2005,209：599－616.

[5] Yu H,Luo L S,Girimaji S S.LES of turbulent square jet flow using an MRT lattice Boltzmann model[J].Computers＆Fluids,2006,35：957－965.

[6] Acharya S,Tyagi M,Hoda A.Flow and heat transfer predictions for film cooling[J].Annals of the New York Academy of Sciences,2001,934（1）：110－125.

[7] TyagiM,Acharya S.Large eddy simulation of film cooling flow from an inclined cylindrical jet[J].Journal of Turbomachinery,2003,125（4）：734－742.

[8] Guo X,SchröderW,Meinke M.Large-eddy simulations of film cooling flows[J].Computers＆Fluids,2006,35（6）：587 －606.

[9] Renze P,Schröder W,Meinke M.Large-eddy simulation of film cooling flows with variable density jets[J].der Flow, Turbulence and Combustion,2008,80（1）：119－132.

[10] Sakai E,Takahashi T,Watanabe H.Large-eddy simulation of an inclined round jet issuing into a crossflow[J].International Journal of Heat and Mass Transfer,2014,69：300－311.

[11] Nvidia Corporation.NVIDIA CUDA compute unified device architecture programming guide（Version 0.8.2）[EB/OL].[2015－01－18].http：//moss.csc.ncsu.edu/～mueller/cluster/nvidia/0.8/NVIDIA_CUDA_Programming_Guide_0.8.2, pdf,2007－04－24.

[12] Cercignani C.Theory and application of the boltzmann equation[M].Scottish Academic Press,London,UK,1975.

[13] Bhatnagar P L,Gross E P,Krook M.A model for collision processes in gases.I.Small amplitude processes in charged and neutral one-component systems[J].Physical Review,1954,94（3）：511－525.

[14] Galperin B,Orszag S A.Large eddy simulation of complex engineering and geophysical flows[M].New York：Cambridge University Press,1993.

[15] Hou S,Sterling J,Chen S,Doolen G D.A lattice Boltzmann subgrid model for high Reynolds number flows[J].Pattern Formation and Lattice Gas Automata,1996,6：151－166.

[16] Somers JA.Direct simulation of fluid flow with cellular automata and the lattice-Boltzmann equation[J].Applied Scientiic Research,1993,51（1/2）：127－133.

[17] Wang X,Shangguan Y,Ondera N,Kobayashi H,Aoki T.Direct numerical simulation and large eddy simulation on a turbulentwall-bounded flow using lattice Boltzmann method and multiple GPUs[J].Mathematical Problems in Engineering, 2014：742432.

[18] Ogawa S,Aoki T.GPU Computing for 2-dimensional incompressible-flow simulation based on multi-grid method[J].Transactions of JSCES,2009：20090021.

[19] Wang X,Aoki T,Multi-GPU performance of incompressible flow computation by lattice Boltzmann method on GPU cluster [J].Parallel Computing,2011,37：521－535.

[20] Pope SB.Turbulent flows[M].Cambridge：Cambridge University Press,2000.

[21] 邱翔,刘宇翔.湍流的相干结构[J].自然杂志,2004,26（4）：187－193.

[22] Dubief Y,Delcayre F.On coherent-vortex identification in turbulence[J].Journal of Turbulence,2000,1（1）：1－22.

[23] Özcan O,Larsen P S.An experimental study of a turbulent jet in cross-flow by using LDA[M].Lyngby：DTU Mechanical Engineering,2001.

[24] Özcan O,Larsen P S.Laser Doppler anemometry study of a turbulent jet in crossflow[J].AIAA Journal,2003,41（8）：1614－1616.

High-Performance Numerical Simulation of Jet in Cross-Flow Based on Lattice Boltzmann M ethod

SHANGGUAN Yanqin,WANG Xian,LIYueming
（State Key Laboratory for Strength and Vibration ofMechanical Structures,School of Aerospace, Xi′an Jiaotong University,28 Xianning West Road,Xi′an 710049,China）

Large eddy simulation（LES）with 1.12×108mesheswas performed on three-dimensional jet in cross-flow（JICF）using lattice Boltzmann method（LBM）and multiple Graphic Processing Units（Multi-GPUs）.Reynolds number based on free-stream velocity and jet diameter is 4 000,streamwise inclination angle of jet isα＝30°,and jet-to-cross-flow velocity ratio is set as 0.5.Validity and feasibility of LBM-LESon simulating jet in cross-flow were verified by reasonable qualitative and quantitative results.Fine coherent structures were captured by large-scaled simulation which benefits study on mixing mechanism of jet-in-cross-flow（JICF）.Moreover,6 K20M GPUs were adopted in simulation and it took 15 402 seconds for LBM-GPU solver to simulate 71 680 LBM steps resulting in calculated performance of 521.24 MLUPS.

lattice Boltzmannmethod（LBM）；large eddy simulation（LES）；multiple Graphic Processing Units（Multi-GPUs）；jet in cross-flow（JICF）

1001-246X（2015）06-0669-08

O358

A

2015－03－11；

2015－03－14

国家973计划（2003CB30570202）和国家自然科学基金（11302165）资助项目

上官燕琴（1991－）,女,博士研究生,主要研究方向：湍流的数值模拟,E-mail：sgyq.6510336＠stu.xjtu.edu.cn