基于汽车座椅导轨试验模态的结合部刚度优化

2015-12-31余慧杰丁晓红

机械工程与自动化 2015年3期

张晨，余慧杰，丁晓红

（上海理工大学机械工程学院，上海 200093）

0 引言

研究表明，振动问题60%来自结合部［1］，虽然结合部对整机动态特性影响巨大，但是由于结合作用机理相当复杂，其参数往往无法准确识别。随着有限元技术的发展，仿真分析已成为研究动态特性问题的新方法，但是结合部建模的准确性亦成为阻碍仿真技术发展的瓶颈。因此，对结合部有限元建模方法的研究自然成为一个重要的课题与研究方向。

汽车座椅导轨是座椅与车身之间的连接件，在汽车行驶过程中若导轨产生明显异响将使乘客对整车质量留下糟糕的印象。在对座椅各主要连接部件分析的基础上，可以确定导轨内部钢珠与内外轨之间结合部的动态特性是振动噪声的主要来源。由于钢珠位置处于导轨内部，难以通过试验方式获取结合部参数，因此在仿真建模时无法给出结合部参数。为此，本文以汽车座椅导轨为例，阐述一般有限元模型结合部建模时快速获取接触刚度的方法。该方法将模态试验技术和有限元方法相结合，并运用优化方法对结合部参数进行反推。

1 结合部建模及接触刚度理论计算方法

目前对于结合部的建模方法，若简化处理则有刚性连接与接触对；较为准确的模拟方法则有等参数接触单元与弹簧－阻尼单元［2］。其中，刚性连接完全不考虑接触部位的动态特性，只适用于整体的宏观研究；接触对模拟则以摩擦因数表征接触关系，但对每种接触形式无法给出合适的摩擦因数；等参数接触单元通过单元节点的相对位移推导出单元刚度矩阵，但该方法不考虑各节点之间的耦合作用，目前只在整机的仿真计算中进行验证；弹簧－阻尼单元以刚度和阻尼来表征结合部的动态特性，但是刚度和阻尼难以准确获取，阻碍了该方法的广泛应用。

本文介绍的方法不同之处在于通过有限元优化技术快速反推结合部参数，以弥补传统弹簧－阻尼建模方法的不足。一般而言阻尼对系统的固有频率与振型影响较小，所以本文所述方法中不对接触阻尼进行优化，建模时所需的阻尼参数由模态试验中测得的模态阻尼比来代替。目前接触刚度的识别多采用动态特性试验法或理论计算法。动态特性试验法对结合部结构依赖较高，不适用于装配不便的结构，因此该方法的使用受到很大的限制。而理论计算法，接触刚度kN可以由作用在弹性体上的法向压力F除以法向趋近量δN获得，即：

根据赫兹接触理论，弹性力学中给出了两个弹性体之间的法向趋近量的计算公式［3］：

图1为汽车座椅导轨切面垂向受力示意图。其中，各钢珠所受弹性力分别为F1、F2、F3、F4，α＝45°，Fz为通过座椅传递至导轨的垂向外载荷。对于内轨，根据静力平衡条件有：

其中：z为单列滚道内钢珠数量。

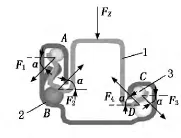
图1 导轨垂向受力示意图

类比接触轴承的支承刚度计算方法［5］，在Fz的作用下，钢珠A的弹性趋近量应等于钢珠B的弹性恢复量，并且弹性体在某一方向上的总变形应该等于各分力作用在该方向的变形之和。另外由赫兹接触理论可知，弹性体的法向趋近量正比于其法向作用力的2/3次方，即：

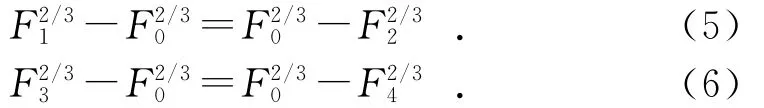
其中：F0为预载荷下单个钢珠所受的法向力。

在z、α、Fz、F0都为已知量时，根据式（3）～式（6）可以求出单个钢珠所受的法向压力。当求得各法向力之后可以根据公式（1）求得接触刚度kN。

直线滚子导轨横向与切向受力的刚度计算方法与垂向类似，这里不再赘述。通过以上的计算方法，即可建立直线滚子导轨结合部动态特性参数模型。由此可见，理论计算方法过程繁琐，且受赫兹接触理论假设的约束，未考虑接触相对滑移等问题，因此理论计算法无法满足结合部建模的通用性、快速性需求。

2 座椅导轨实物模态试验

试验模态分析主要基于线性振动理论，通过试验将采集的系统输入与输出信号经过参数识别获得模态参数。本次测试中采用DH5927动态测试分析系统，试验中将导轨用软绳悬挂起来近似模拟自由状态，用锤击法按照激励点移动、响应点固定的方式来测试传递函数。

由振动力学可知，在结构的振动过程中引起振动的主要因素是低阶模态，并且由于实际结构中阻尼的存在，较高阶模态的振型将迅速衰减。另外，导轨对路面激励敏感频率为40Hz以下的低频段，故我们找到前2阶模态固有频率及振型，并以此作为刚度优化中的优化目标值。若需对更多阶模态进行研究，方法相同。表1为试验模态固有频率及阻尼比，图2为试验模态振型图。

表1 试验模态固有频率及阻尼比

3 座椅导轨有限元模型

本次FEA模型的建立是基于Altair公司的HyperMesh软件进行的。在HyperMesh中用壳单元对薄壁件进行数学离散。在该模型中，外轨长450mm，内轨长402mm，采用基本尺寸为5mm×5mm的CQUAD4单元，并赋予壳单元实际部件的厚度。模型中共有节点7 913个、单元7 406个，选取各向同性材料建立材料模型，其中弹性模量E为210GPa，泊松比为0.3，密度为7 900kg/m3。汽车座椅导轨有限元模型如图3所示。

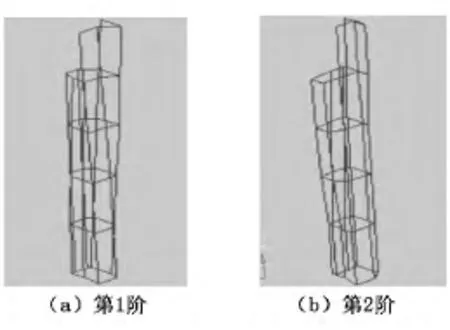
图2 试验模态振型

导轨内部钢珠的模拟是本次建模的关键，为简化问题，我们将钢珠视为刚体。建模过程中在24个钢珠位置嵌入弹簧单元（CBUSH单元），每个钢珠由一个CBUSH单元（CBUSH单元两端点位置重合）和两个RBE2单元（刚性单元）构成。根据弹簧单元位置的对称性，将其分成4组。弹簧单元可赋予6个自由度（3个轴向线位移自由度，3个旋转角自由度）方向刚度。需要注意的是CBUSH单元需要赋予一个局部坐标系，其6个自由度方向也是相对于局部坐标系而言的。

图3 汽车座椅导轨有限元模型

4 基于试验模态的刚度优化

在HyperWorks中的OptiStruct模板下用Lanczos法按质量矩阵归一化对导轨模型进行自由模态实特征值提取。初始分析中为弹簧给定一组初始刚度值。在刚度给定过程中，发现4组弹簧旋转角自由度方向刚度对计算模态结果无影响，故只考虑4组弹簧12个轴向线位移刚度。当12个刚度都指定为500N/m时，除去前6阶刚体模态之后，导轨系统前2阶模态固有频率如表2所示。

表2 给定初值计算所得模态固有频率值

初始分析完成之后，在OptiStruct模板下进行尺寸优化。以试验模态1、2阶固有频率为目标，弹簧单元刚度值为设计变量，运用最小二乘法进行刚度优化。

4.1 设计变量

设计变量为要优化的结合部接触刚度，即4组弹簧的各方向刚度Kx、Ky、Kz，共12个设计变量。给定500 N/m为初始值，设定设计变量的变化范围在1N/m～1 000N/m。

4.2 设计目标

用最小二乘法最小化如下目标函数：

其中：Fi、fi分别为试验与计算模态第i阶固有频率。

4.3 优化结果分析

优化后目标函数最小二乘偏差为2.59×10－5Hz，优化后的固有频率计算结果见表3，优化计算得到的弹簧刚度见表4。

表3 优化后的导轨模态固有频率值

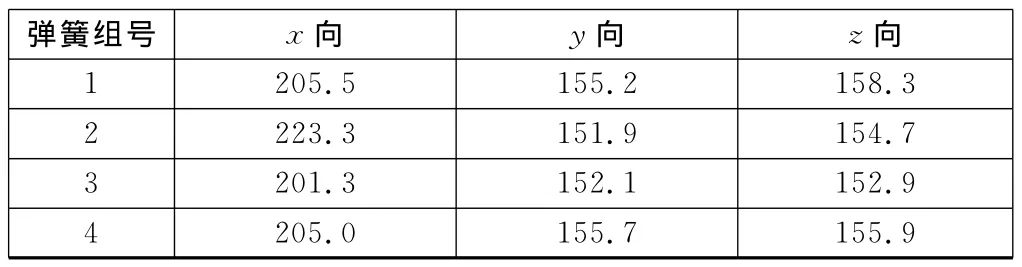
表4 优化后弹簧刚度N/m

优化后的第1、2阶模态振型与试验模态振型对比如图4所示。

经过对比，优化后导轨系统模态振型与试验模态对应阶次的振型相吻合，所以我们认为在此过程中所得优化后的弹簧刚度即为所要得到的结合部等效接触刚度。

5 结束语

通过模态试验技术与有限元模态分析相结合的方法，对汽车座椅导轨结合部接触刚度进行了优化，得到了该导轨各阶固有频率及振型。通过对比研究，说明该模型的参数优化结果是可取的，模型的建立是成功的。该研究结果表明，基于实测参数的有限元优化方法能够较好地解决结合部等效参数获取问题，从而为一般结合部建模提供了解决方案。