大跨度柱壳屋盖基于半无矩理论简化计算方法研究＊

白志强，刘 元

（1.潍坊学院，山东 潍坊 261061；2.中国建筑标准设计研究院有限公司，北京 100048）

柱壳由于其良好的受力性能，在船舶工业中应用较为广泛，关于柱壳的受力分析，很多学者基于经典弹性力学理论，对柱壳的解析解法进行了积极的探索［1-2］。近几十年来，壳体结构在建筑中的应用愈加广泛，尤其是球面网壳、扁网壳等钢网格结构在大跨建筑中应用日趋成熟。而对于混凝土柱壳结构的应用比较少，因此，积极探索混凝土柱壳结构的简化分析方法对推动柱壳结构在工程实践中的应用是非常必要的。

薄壁柱壳由于其在纵向曲率为零，在计算、设计、制造及施工过程中比双曲扁壳结构要简单方便的多，这也是环向开敞的柱壳可应用于各种工业与民用大跨度结构中的优势之一。一般来讲，顶盖柱壳的计算是相当繁琐的，但对于薄壁柱壳，面内次要方向的弯矩应力相对于其他应力分量很小，可以忽略，可考虑半无矩理论的简化方法进行计算。单建［3］以结构力学杆系结构为例，分析了无矩解法的误差问题。徐烈煊［4］采用半无矩理论简化分析方法计算了直线边带有直梁的柱壳结构受力，并与Donnell弯曲理论和Schorer简化理论所得结果进行了比较。本文基于弗拉索夫提出的半无矩理论，求解一对边简支的柱面薄壳屋盖结构的内力和位移，并与有限元分析结果进行了比较。

如果圆柱壳的直线边长度a与圆柱壳在水平面内的投影宽度b 之比大于1.5，纵向荷载q1=0，环向荷载q2及法向荷载q3都只沿环向变化，即可按半无矩理论简化计算。半无矩理论是丹尼尔弯曲理论基本假设的进一步简化：1）在垂直于母线方向横截面上，弯矩和扭矩可以忽略（M1=M12=0）；2）不计中面的环向线应变和切应变，也就是取ε2=ε12=0，并且不计环向曲率的改变，即x2=0（于是α为常量的横截面的中线不变形，而且保持垂直于纵线）；3）忽略泊松比的影响，即μ=0。

1 柱壳半无矩简化分析方法的基本方程［5］

圆柱壳的尺寸如图1所示：

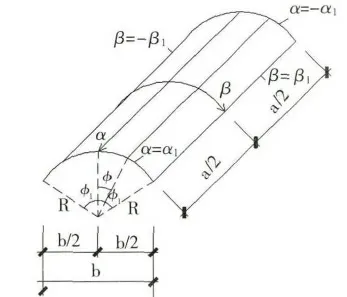
图1 柱壳坐标及符号

引入无量纲坐标：

圆柱壳在q1q2q3作用下的平衡微分方程可以写成：

由物理方程及几何方程得出方程如下：

图2 柱壳微分单元受力

而边界条件可以表示为：

基于之前的假定，壳体横截面上的正应力和直梁横截面上的弯曲应力一样，和截面的M 成正比。此柱壳横截面弯矩图沿纵向呈抛物线变化（见图2），故M 正于与（α2-α12），也就正比于（ξ2-）。由于柱壳横截面上的M1已经假定为零，可见上述的M 只与FT1即δσ1的合成，而

其中f（φ）=C1φ3+C2φ2+C3φ+C4。

将FT1表达式代入基本方程，结合边界条件可得出：

此处，由于C6C7C8为待定常数，已起到附加常数的作用，故积分式的附加常数可以取零。

柱壳中面位移的表达式为：

八个待定常数C1至C8可以由边界条件完全确定。在对称荷载作用下，q2（φ）是φ 的奇函数，q3（φ）是φ 的偶函数，因而u，ω，FT1，FT2，M2是φ 的偶函数，而υ，FT12，FS2是φ 的奇函数，这时有C1=C3=C5=C7=0，只需由四个方程求C2，C4，C6，C8。若在反对称荷载作用下，同理可利用上述性质简化计算相应四个待定常数C1，C3，C5，C7。对于一般荷载，可分解成对称和反对称荷载，叠加求之。

2 算例分析

圆柱壳屋面，厚度0.15m，拱的半径为20.0m 的圆曲线，长度分别取为36m 和60m（对应的，半圆心角30°，侧向长边方向铰支，曲边自由，密度2500kg／m3，C30混凝土，材料弹性模量30GPa，试分析其在自重作用下的内力以及变形情况。

在屋盖自重作用下，自重荷载为对称荷载，满足以上叙述的简化求解条件。

按半无矩理论简化方法求得跨中柱壳顶点处（α=β=0）的平行直线边的内力FT1和径向位移ω。

同时，采用ansys软件建立有限元模型，两简支端曲梁采用beam4单元模拟，柱壳屋盖采用shell181单元模拟，考虑泊松比为0.2，在cylindrical坐标系下，得到跨中柱壳顶点的平行直线边的内力FT1和径向位移ω。结果见表1。

表1 两种计算方法所得FT1和ω

3 结果分析

通过以上的计算结果可以看出，对应沿母线方向的FT1值，半无矩理论算得的结果值比有限元算的的结果均偏大，跨度为36m 的结构运用半无矩理论的计算结果大了近60%，FT1大了跨度为60m 的柱壳结构结果偏大了一倍。主要原因在于采用半无矩理论简化计算时，过多的近似 （不考虑泊松比，不考虑环向应变等）使得计算结果过于保守。

同时在进行径向位移计算的过程中，由于半无矩理论运用的前提假定，使得中性面不发生变形，顶点处的最大位移为-0.0293m 和-0.2260，而ansys分析结果同位置处的位移为0.0182m 和0.01677m（沿径向背向圆心）。但由于在有限元建模过程中，材料属性采用各向同性材料模拟，在计算过程中考虑了环向切应变和环向线应变，考虑了环向曲率的改变，因此变形结果在柱壳顶点有沿径向背向圆心方向的位移，在柱壳的直线边界处，沿径向的位移最大，分别达到-0.172m 和-0.282m （方向沿径向指向圆心）。如图3、图4所示。

图3 36m 跨柱壳处截面的变形

图4 60m 跨柱壳处截面的变形

从结果比较来看，基于半无矩理论的简化方法FT1计算结果较之数值计算结果明显偏大；位移计算结果尽管在同一个数量级内，但由于简化方法在计算过程中忽略了环向线应变和切应变，同时忽略环向曲率等过多的近似，使得计算的位移变形形态和有限元实体建模分析所得的变形结果又较大的差异，而有限元的变形趋势基本符合实际的受力特点，有柱壳弧线被 “压扁”的趋势，如图5和图6。

图5 36m 跨柱壳的变形云图

图6 60m 跨柱壳的变形云图

4 结论

（1）通过比较两种方法所得的结果，可得知基于半无矩理论的简化计算所得跨中顶点处内力值FT1结果与数值分析方法结果保持在一个数量级之内，简化方法所得结果偏保守。计算的径向位移变形分布与数值分析结果有明显差异。由于数值分析计算结果并没有过多的近似假定，ansys建模过程中，选择各构件模拟单元时，尽可能地反映各构件的实际受力特点，因此有限元分析结果能够较精确地反映柱壳结构实际受力情况和变形情况。

（2）基于本文的分析可知，半无矩理论的分析结果与有限元分析结果存在明显偏差，建议在概念设计阶段可通过半无矩理论简化方法近似估计FT1的受力及ω 的取值，在精细分析阶段，应对误差足够重视；对于两端简支柱壳结构的精确计算，有限元分析方法应作为首选方法。

［1］王燕舞.对称双圆弧柱壳强度及稳定性解析计算方法研究［D］.哈尔滨工程大学，2004.

［2］姚文.圆柱壳结构在非均匀荷载作用下的强度分析［D］.哈尔滨工程大学，2007.

［3］单建，宋九祥.结构力学中拟无矩状态的计算问题［J］.力学与实践，2005，27（1）：70-71.

［4］徐烈煊.圆柱壳的半无矩理论分析［J］.武汉理工大学学报，2004，26（1）：72-75.

［5］徐芝纶.弹性力学（上册）［M］.4版.北京：高等教育出版社，2006：301-330.