基于CFD的非标准孔板流量计的数值模拟

基于CFD的非标准孔板流量计的数值模拟

赵奇，牛志娟,杨雪峰

(四川大学化学工程学院，四川成都610065)

摘要：为了获得一种在性能和节能方面都较优的非标准孔板，以计算流体力学(CFD)为工具，模拟了标准孔板流量计与一类两通道非标准孔板流量计的内部流场，并探究了两大类孔板分别在β=d/D为0.5和0.7时的流出系数随雷诺数的变化规律，并与由Reader-Harris/Gallagher(1998)公式计算出的流出系数进行比较。结果表明：数值模拟的结果与按理论公式计算的结果相差较小，反映了模拟结果的正确性,比较两类孔板的模拟结果可知，两通道非标准孔板具有低临界雷诺数，永久压降低等优点。因此模拟结果为孔板的理论分析和实验研究提供了新的思路。

关键词：非标准孔板；计算流体力学；孔板流量计；数值模拟；流出系数；低临界雷诺数

中图分类号：TH814`+.5

文献标识码：A

文章编号：1002-6339 (2015) 05-0453-04

Abstract：In order to obtain a kind of the non-standard orifice flowmeter that has good performance, the author simulated the flow field of the standard orifice flowmeter and a class of two channels non-standard orifice flowmeter based on computational fluid dynamics (CFD). And the regular that the discharge coefficient of the two categories of orifice changing with the Reynolds number in β= 0.5 and β=0.7 are obtained. The results show that the numerical simulation results only have a slight difference compared with the theoretical results. So it show that the reliability of the numerical simulation. According to the calculated results,the two channels,non-standard orifice plate with many advantages.compared with the standard orifice plate, such as , low critical Reynolds number, low permanent pressure drop etc. And the simulation results can provide the reference for the theoretical analysis and experimental research of orifice plate.

收稿日期2014-10-31修订稿日期2014-12-04

作者简介：赵奇(1990~)，女，硕士研究生，研究方向为流量计量技术。

Numerical Simulation of the Non-standard Orifice Flowmeter based on CFD

ZHAO Qi,NIU Zhi-juan，YANG Xue-feng

(College of Chemical Engineering,Sichuan University,Chengdu 610065,China)

Key words：the non-standard orifice;computational fluid dynamics(CFD);orifice flowmeter;numerical simulation;discharge coefficient;low critical reynolds number

以节流装置为检测件的差压式流量计称之为节流式差压流量计,孔板流量计因其具有耐用，安装简便，无移动部件,并在极恶劣的条件下都能使用等众多优点，成为目前应用最多的一种差压式流量计[1]。孔板流量计根据其是否按照标准文件的要求来进行设计、制造、安装和使用被分为标准孔板流量计和非标准孔板流量计两大类[2]。标准孔板成熟程度高，无需实流校准，但由于现场工况极其复杂，标准孔板流量计往往不能完全满足要求，故出现了各类非标准孔板流量计[3]。为了获得性能较优的非标准孔板，在最近的数十年里，国内外学者提出了多种新型结构的孔板并研究了它们的相关性能。如Ann Mclver[4]研究了V型内锥流量计流出系数的稳定性；Shanfang Huang[5]等人通过实验研究了孔板厚度，开孔率，上游直管段长度等对多孔流量计流出系数的影响；钟伟[6]等提出了一种纺锤体流量计，并通过Fluent数值分析了其特殊结构对流体流动的作用等。在这一背景下，本文以计算流体力学(CFD)为工具，分别分析了标准孔板流量计和两通道非标准孔板流量计的内部流场，探究了不同类型孔板流出系数随雷诺数的变化规律，比较了不同孔板对前后直管段的要求的差异，从而为非标准孔板流量计的设计与发展提供一定依据，并提高测量的准确性。

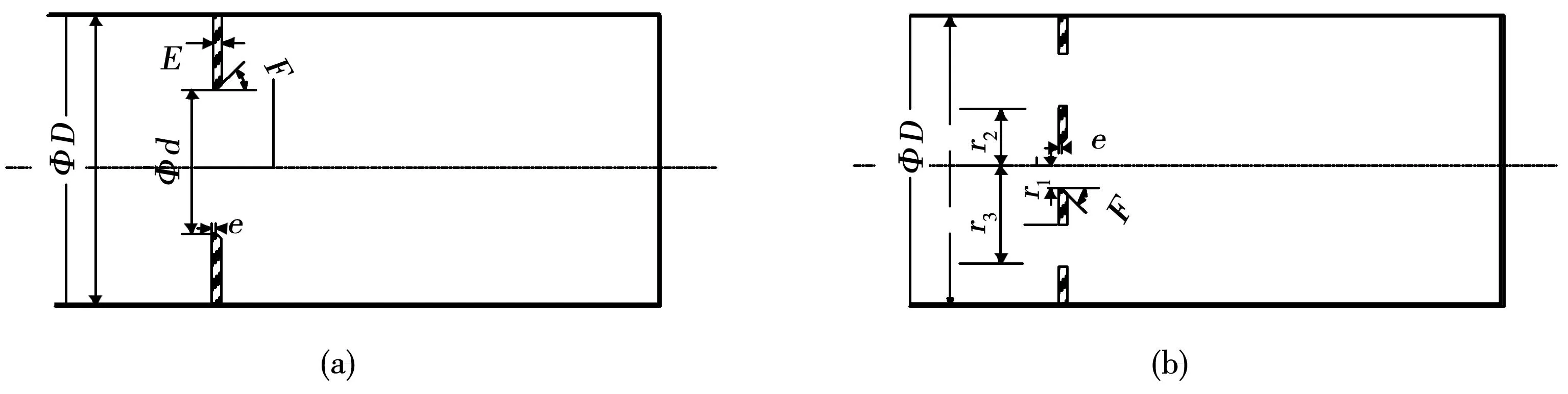
图1　两类孔板结构简图

1理论基础

1.1　孔板流量计

图1中的(a)、(b)分别为标准孔板,两通道非标准孔板及管道的简图。由于这两类孔板都是因为流体通过孔板时因流通面积的突然收缩而加速，导致孔板前后产生压力差，故它们都可以通过测定孔板前后的压差来计算管道中的流量[7]，它们唯一的区别就是最小流通截面不一样。在已知有关参数的条件下，根据流动流体的连续性原理和伯努利方程可以推导出差压与流量之间的关系。其基本公式为

(1)

式中Qv——体积流量/m3·s-1；

C——流出系数；

β——直径比；

d——工作条件下节流孔直径/m；

Δp——差压/Pa；

ρ——流体密度/kg·m-3。

1.2　计算流体动力学

计算流体动力学(Computional Fluid Dynamics)，简称为CFD，主要是通过计算机数值计算和图像显示，对含有流体流动和对流传热等相关物理现象的系统来进行分析[8]。CFD最大的优点是它不受物理模型和实验模型的限制，能够给出全部流场范围内的详细信息，并能够模拟出实验所不能达到的条件等优点[9]。故CFD技术广泛应用于模拟流体的流动，并为其理论分析和实验研究提供新的思路。

2数值模拟

2.1　建模,网格划分

利用孔板轴对称性的特性，在圆柱坐标系下建立它们1/2的实体模型，取压方式采用D-D/2取压,截面积比是指开孔截面积与管道截面积之比(见表1、表2)。根据标准孔板流量计的安装要求,孔板前直管段长度为10D，后直管段长度为5D。本文所用的流体介质为常温的液态水。

表1标准孔板尺寸

孔板编号截面积比(A0/A1)d/mmD/mm1#0.25501002#0.4970100

表2两通道非标准孔板尺寸

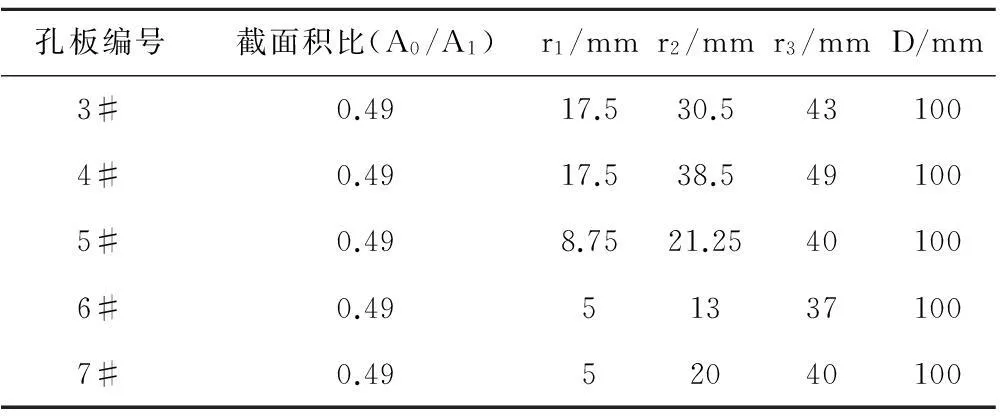
孔板编号截面积比(A0/A1)r1/mmr2/mmr3/mmD/mm3#0.4917.530.5431004#0.4917.538.5491005#0.498.7521.25401006#0.49513371007#0.4952040100

为了获取孔板前后详细的流场变化情况，首先在壁面附近划分边界层网格，并对靠近孔板的网格进行局部加密,离孔板越远，网格越稀。

图2　网格划分图

2.2　边界条件及模型的求解

该模型的边界条件包括速度入口、压力出口，轴对称边界以及无滑移的壁面边界。本文选用Standard k-ε湍流模型，并在近壁面区域采用标准壁面函数(Standard Wall Function)进行处理。在求解离散方程组的压力速度耦合时选择了SIMPLE算法，动量和湍流动能分别采用的是二阶迎风与一阶迎风的差分格式。该模型的控制方程为

·u=0

(2)

·(ρuui)=

(3)

(4)

(5)

式中k——湍动能;

ε——湍动耗散率;

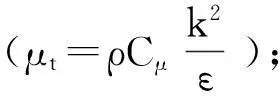
Gk——由层流速度梯度而产生的湍流动能;

C1ε=1.44,C2ε=1.92,Cμ=0.09,σk=1.0,σε=1.3。

3结果分析

3.1　流出系数C

流出系数C定义为通过孔板的实际流量值与理论流量值的比值，它与管道内雷诺数的大小、截面积比，取压方式以及管道情况等众多因素有关[10]。在选用孔板流量计时，应保证它的测量范围落在流出系数C为常数的范围内，这样才能确保流量测量的准确性。因此流出系数C是评价孔板流量计性能至关重要的参数[11]。在GBT 2624-2006中流出系数C用Reader-Harris/Gallagher(1998)公式[12]进行计算

(6)

式中β——直径比；

ReD——根据D计算出的雷诺数。

在实际的应用中，孔板的临界雷诺数越小，它的测量范围就越宽。故可以改变这类两通道非标准孔板中心的流通截面和周边的环形流通截面的尺寸以及位置来确定最优形状的孔板，使得临界雷诺数尽可能的小，以增大流出系数的常数区范围。在图3中几种非标准孔板的流出系数都比相应的标准孔板大，并且某些尺寸的非标准孔板的流出系数较标准孔板能在较小的雷诺数下达到稳定，这说明它们有更宽的应用范围。而编号4#的孔板具有最小的临界雷诺数,使得它在低雷诺数下测量时也有较高的重复性。

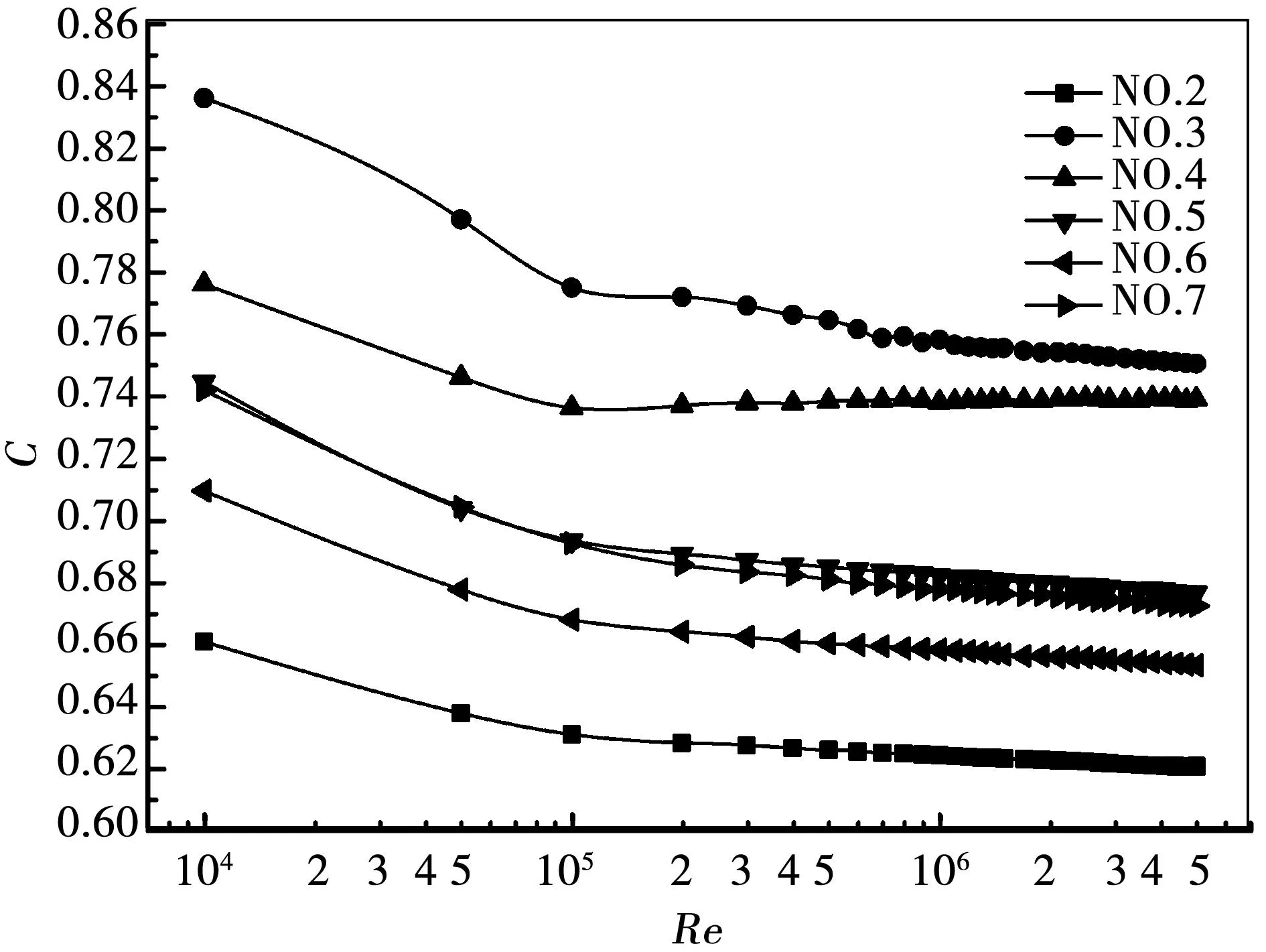
图3　β=0.7的孔板流出系数的比较图

3.2　速度流场与压力流场

通过Fluent模拟了几种不同孔板前后的流场变化，由模拟结果可知流束经过不同孔板后速度都明显增大，当距离孔板一段距离后速度恢复正常，压力相应降低。根据孔板流量计的工作原理可知这是由于管道流通截面积的突然缩小，迫使流体的部分压力能转换为动能。经计算可得，编号3#，5#，6#，7#孔板比相应的标准孔板的永久压降分别降低了8.71%，12.81%，10.99%，10.1%，4#孔板却升高了7.67%。

从图4可以看出两通道非标准孔板后的流场更为稳定，压力恢复更快，这可能是因为周边的环形流通截面起到了整流的作用，从而减少了孔板后涡流的形成和紊流的摩擦、振动。并且4#孔板压力恢复得最快，对直管段的要求最低，故能省去大量的管道费用。因此这类孔板既能在管道费用方面减少开支，并且还能降低能量耗费，是一类节能的非标准孔板。

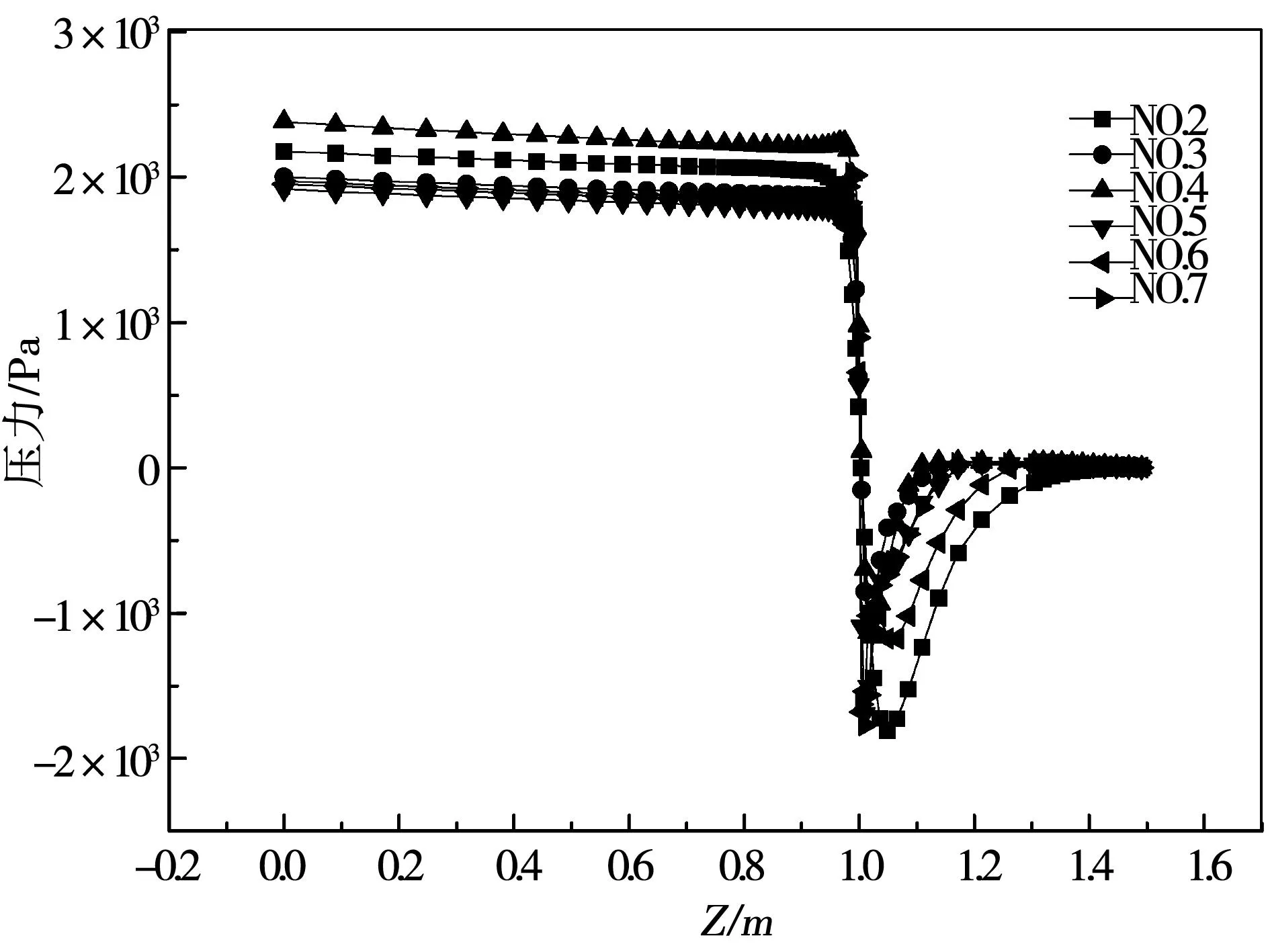
图4　β=0.7的孔板中心轴线上压力分布曲线图

图5中孔板的永久压降在雷诺数为103到106的区间范围内增加的非常缓慢，当雷诺数大于106后，孔板的永久压降急剧上升，这说明孔板流量计在一定雷诺数范围内工作时比较经济。经计算还可知孔板下游压力恢复点离孔板上游端面的距离Z在雷诺数较小时随着雷诺数的增加而不断变大，当雷诺数达到一定数值时，压力恢复点的距离便维持在一个稳定值。

标准孔板的流线图前直管段速度分布较均匀，之后所有流体集中到唯一的中心孔,从而导致在孔板下游靠近壁面附近的区域有一个被拉长的漩涡。两通道非标准孔板在前直管段的流线与标准孔板的一样，但当流束流经非标准孔板后被分成两股射流，不仅在近壁面有回流区而且在环形流通截面与中心孔道流通截面之间也有漩涡的存在，但总体来说两通道非标准孔板的漩涡少于标准孔板的。孔板的压力损失之所以很高主要是因为这些涡流的能量耗散所造成的[13]，故两通道非标准孔板的压力损失较标准孔板的小。而近壁面回流区与射流之间的回流区的大小主要取决于中心孔与周边环形截面的尺寸。

4结论

在本文中，通过CFD模拟了一类两通道的非标准孔板与标准孔板的运动流场，并通过改变非标准孔板中心孔和周边环形流通截面的尺寸与位置，确定了这类孔板的较优结构参数。探究了孔板的流出系数与雷诺数的关系，由模拟结果可知两通道非标准孔板既能在管道费用方面减少开支，又能降低能量耗费，故这类孔板较标准孔板能节约较大的运行成本，并且某些性能在一定程度上优于标准孔板。在实际应用中我们可根据不同的需求选择不同的孔板。

参考文献

[1]侯祥松.电炉炼钢冶炼周期中烟气热力学特性的变化规律[J].冶金能源，2010，29(1)：28-31.

[2]周何.电炉余热锅炉热力计算软件的开发[D].沈阳：东北大学，2011.

[3]杨彬，沈士兴，王方荣,等.电弧炉余热锅炉设计[J].工业锅炉，2011(3):20-23.

[4]曹先常.电炉烟气余热回收利用技术进展及其应用[C].无锡:第4届中国金属学会青年论文集，2008:418-423.

[5]杨振国，刘青，谢银幕.电炉流程中热管式余热回收[J].北京科技大学学报，2011，33(10)：87-92.

[6]何立波.炼钢电炉余热发电技术[J].工业炉，2013，35(2)：16-18.

[7]陈兴卫.低温热水发电用正压外壳型无刷励磁汽轮发电机的设计[J].大电机技术，2014(3)：22-25.

[8]陶务纯.50 t炼钢电弧炉烟气余热回收系统的设计应用[J].工业加热，2012，41(3)：56-59.

[9]刘改娟.100 t电炉烟气余热回收实践[J].冶金动力，2008，29(5)：36-39.

[10]赵钦新，周屈兰，谭尊厚,等.余热锅炉研究与设计[M].北京：中国标准出版社，2010.

[11]李冬庆，张华，米静,等.转炉饱和蒸汽发电系统及其参数选择[J].热力发电，2008，37(11)：5-11.