一种槽式聚光器追日误差补偿方法
2015-12-30卞新高
王 锐,卞新高
(1.河海大学机 电工程学院,江苏 常州 213022;2.河海大学 南通海洋与近海工程研究院,江苏 南通 226019)
一种槽式聚光器追日误差补偿方法
王 锐1,2,卞新高1,2
(1.河海大学机 电工程学院,江苏 常州 213022;2.河海大学 南通海洋与近海工程研究院,江苏 南通 226019)
为了消除槽式聚光器回转轴位置偏差对太阳跟踪精度产生的影响,以南北布置的槽式聚光器为例,通过分析槽式聚光器回转轴在安装时或长期工作之后产生的位置偏离,建立回转轴偏离理想位置的数学模型,推导出太阳相对回转轴的高度角和方位角计算公式,进而对回转轴偏离产生的误差进行补偿。算法适用于任意方向布置的槽式聚光器的跟踪角度计算。
槽式聚光器;太阳跟踪;高度角;方位角;跟踪误差;误差补偿
随着经济发展和社会进步,人们对能源的需求也日益增大。利用可再生能源成为人们的最佳选择[1]。太阳能以其洁净、高效、广阔的优点在新能源的开发研究中占据首要地位[2]。而槽式聚光器作为主要聚光方式之一,广泛应用于槽式太阳能光热发电技术、太阳能锅炉中。目前,槽式聚光器的应用具有规模大、工作时间长的特点,其高昂的建造成本决定其在长期运作后方可收益,要求其跟踪系统适应太阳光线变化的缓慢性、间歇性及环境天气的变化,做到实时精确跟踪,并且在长期的运作中保持较高的稳定性。因太阳光线的入射角度在地平面坐标系中,用高度角和方位角来表示,这2个角度值与跟踪器所在的经纬度、时间等有关[3-4]。槽式聚光器对太阳光线的跟踪过程是通过调整聚光器回转轴角度将柱形抛物面的法平面与太阳入射方向重合的[5]。一般聚光器安装时,其回转轴的布置有南北方向和东西方向2种方式[6],由于安装误差和长期工作之后地基、结构变形导致聚光器回转轴偏离理想位置,产生跟踪角度偏差。针对太阳跟踪误差,文献[7]将太阳位置算法、GPS和无线传感器网络结合使用提高太阳跟踪精度[7],文献[8]采用引入跟踪角度修正因子方法来补偿太阳二维跟踪误差。本文以回转轴南北方向安装为例,建立槽式聚光器位置偏离后回转轴与太阳入射光线相对位置的几何模型,推导出跟踪太阳光线的回转轴旋转角度补偿方法。
1 误差分析
大规模的槽式聚光器跟踪系统通常采用视日运动轨迹跟踪,是一种程序跟踪系统。系统根据当地的经度、纬度、时间参数,计算出太阳在地平面坐标系中的高度角和方位角[9-10],并通过高度角和方位角结合聚光器的布置情况计算出太阳跟踪角度进行一维跟踪。我国大部分地区处在中纬度地带,槽式聚光器选择南北水平布置,由于安装误差、长期运行后设备本身强度和地理环境变化等原因造成跟踪装置偏离南北水平方向(标准安装位置),计算出的高度角和方位角相对于聚光器回转轴产生误差,使聚光器的实际跟踪位置偏离理论跟踪位置(见图1),降低集热效率[11]。

图1 聚光器跟踪位置的偏离Fig.1 The deviation of solar concentrator tracking position
2 理论模型
2.1 描述回转轴偏离的理论模型
以编码器或倾角传感器所在端(本文中为南端)为原心,正北方向为X轴,正东方向为Y轴,天顶为Z轴,建立左手直角坐标系,定义为回转坐标系,在回转轴未偏离时与地平面坐标系重合。当回转轴偏离后,回转坐标系相应发生旋转偏离,其中X轴始终为回转轴所在方向。见图2,B、C、D分别为A点(回转轴的北端)在X0Y面、X轴、X0Z面上的投影。0A′为回转轴标准安装位置(A′在X轴上),0A为回转轴发生倾移后的任意位置(偏离后X轴方向)。回转轴的倾移由2个参数确定:轴倾角κ(∠A0B)、轴倾方位w(∠B0C)。本文定义:轴倾角κ范围[-90°,90°],A点高于0点(自由端高于编码盘所在端)为正值;轴倾方位角w范围[-180°,180°],正北为0,北偏西为正值。
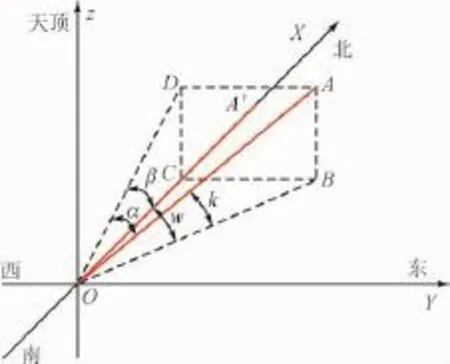
图2 回转轴的偏移Fig.2 The deviation of the rotary shaft
根据图2,按左手法则将坐标系绕Y轴旋转角度κ,再绕Z轴旋转角度w后,0A′旋转到0A位置。坐标系绕Y轴的旋转矩阵[12]为

坐标系绕Z轴的旋转矩阵为:

故回转坐标系的旋转矩阵为

2.2 太阳位置相对于回转坐标系发生偏离的模型
采用回转坐标系代替地平面坐标系来计算太阳位置,等价于把太阳位置按回转轴偏移方向反向偏移。如图3所示,P点为太阳在地平面坐标系中的位置,e、a分别为地平面坐标系中的太阳高度角、方位角;P′为太阳在回转坐标系中的位置,e′、a′分别为回转坐标系中的太阳高度角、方位角(即相对高度角、相对方位角)。

图3 太阳位置的变化Fig.3 The change of the solar position
地平面坐标系中,太阳P坐标[13]为


回转坐标系中,根据
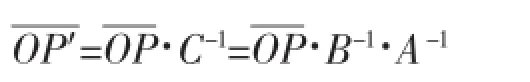
可得太阳P′的坐标为
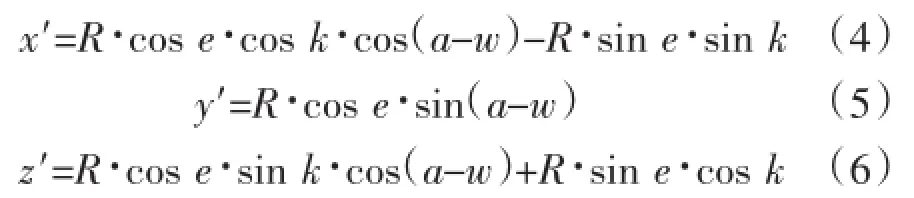
因此,可求得太阳相对高度角e′,相对方位角a′,计算公式为

式(8)中,arctan2定义为保留相对方位角a′正确象限的反余弦函数。
定义函数θ=arctan2(x/y):
当分子x>0,分母y>0时,θ=arctan(x/y);
当y<0时,θ=arctan(x/y)+π;
当x<0,y>0时,θ=arctan(x/y)+2π。
2.3 槽法线角的计算
槽式聚光器对太阳进行一维跟踪,跟踪角度定义为槽法线角,其变化与太阳相对高度角、相对方位角有关,如图4回转坐标系,x0y平面为槽式聚光器基面,Z轴为槽法线零度位置,称为槽式零位。太阳(A点)在基面上的投影为B,太阳在旋转轴所在直线的投影为C,则∠ACB为槽法线角t:
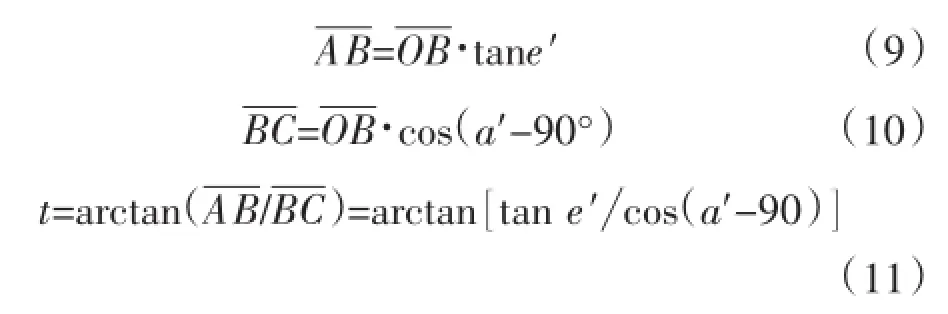
式中:e′为太阳相对高度角;a′为太阳相对方位角;t为槽法线角。
式(7)式(11)适用于计算槽式聚光器任意方向布置的跟踪角度。特别地,当轴倾角为±90°时,聚光器为东西布置情形,如图4(b)所示。
3 实验数据
第1、2节回转轴偏离模型并未考虑原点偏离的情况。这里单独做出分析,见图5,A、B两测试点相距10 m,实测A点经纬度为北纬31.81821°东经119.981 46°,B点经纬度北纬31.818 61°东经119.975 00°,纬度和经度分别相差0.004 00°、0.006 46°,代入跟踪角度计算公式算得角度误差很小,最大误差为0.02°,可忽略不计。在实际运行中,回转轴原点位移误差远远小于10 m,故回转轴偏离模型的建立不考虑原点偏离。

图4 跟踪角度计算示意图Fig.4 Sketch of the tracking angle calculation

图5 原点偏离误差Fig.5 Error of the origin deviation
当轴倾角为0.5°、轴倾方位角为-1°时,采用本文算法计算得出2015年3月28日7:00-19:00南通某地太阳相对高度角、相对方位角以及在回转坐标系中的实际槽法线角,与太阳高度角、方位角及在地平面坐标系中的理论槽法线角作对比,如图5 7所示。

图6 高度角变化趋势及对比Fig.6 Elevation angle trend and comparison
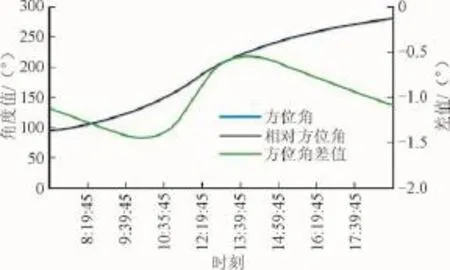
图7 方位角变化趋势及对比Fig.7 Azimuth angle trend and comparison
在图6中,7:00高度角和相对方位角分别为13.25°和13.2°;12:03达到当天最大值,分别为61.28°和60.78°;19:00角度值分别为-9.89°和-9.79°。高度角误差变化趋势与高度角变化趋势相同,其中当天最大角度差发生在12:03,误差为0.5°,最小角度差发生在17:00,误差为0.1°(图6中为负值)。图7中,方位角和相对方位角皆不均匀增大,7:00角度值分别为94.73°和95.84°,19:00角 度值 分别 为280.08°和281.16°,方位角误差范围为[0.53°,1.45°]。图8中,理论槽法线角和实际槽法线角变化范围为[-90°,90°],其中(本文南北布置时)聚光器偏东为正值,偏西为负值。法线角差值曲线成正态分布曲线,12:34误差最大,为0.59°。对于焦距为1 710 mm且配有真空玻璃管直径为120 mm,金属管外径70 mm,内径54 mm的集热管的聚光器,此时聚焦光斑偏离17.60 mm,其误差不可忽略。
4 结语
经实验数据分析对比,本文推导得出的计算公式较好地补偿了回转轴偏离误差;同时可用于任意方向布置的槽式聚光器的跟踪角度计算,当轴倾角为0°,轴倾方位角为-90°,时计算槽式聚光器东西布置的跟踪角度。本文提出的太阳相对位置计算公式与高精度跟踪执行机构结合使用,可以实现太阳的高精度一维跟踪。

图8 槽法线角变化趋势及对比Fig.8 Trough normal angle trend and comparison
[1]张欣,雷震,许栋栋.未来十大新能源[J].江苏电机工程,2014(1):4-6. ZHANG Xin,LEI Zhen,XU Dongdong.Ten new energy in the future[J].Jiangsu electrical Engineering,2014(1):4-6(in Chinese).
[2]陈于平.聚光太阳能发电技术应用与前景[J].电网与清洁能源,2010,26(7):29-33. CHEN Yuping.Application and prospect of concentrating solar energy power plant(CSP)technology[J].Power System and clean Energy,2010,26(7):29-33(in Chinese).
[3]王金平,王军,冯炜,等.槽式太阳能跟踪控制系统的研制及应用[J].农业工程学报,2015(2):45-52. WANG Jinping,WANG Jun,FENG Wei,et al.Deve-1opment and application of sun-tracking control system for parabolic trough solar collector[J].Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE),2015(2):45-52(in Chinese).
[4]尹丹.槽式太阳能热发电装置跟踪控制系统研究[D].哈尔滨:哈尔滨工业大学,2012.
[5]张先勇,舒杰,吴昌宏,等.槽式太阳能热发电中的控制技术及研究进展[J].华东电力,2008(2):135-138. ZHANG Xianyong,SHU Jie,WU Changhong,et al. Control technology and its research development for solar parabolic through power generation[J].East China electric Power,2008(2):135-138(in Chinese).
[6]裴刚,符慧德,季杰,等.槽式太阳能聚光集热系统在不同跟踪模式下的对比[J].太阳能学报,2010(10):1324-1330. PEI Gang,FU Huide,JI Jie,et al.Performance comparison of a trough solarconcentration system in different tracking modes[J].Acta Energiae Solaris Sinica,2010(10):1324-1330(in Chinese).
[7]JOSHUA D.FREEMAN,JIBIN THOMAS VARGHESE,DIVYA PULLARKATT.WSN based tracking for a concentrating solar thermal energy system[J].IEEE Conference on Technologies for Sustainability,2013:203-207.
[8]周来所.定日镜跟踪误差补偿方案的研究[D].南京:河海大学,2011.
[9]IBRAHIM REDA,AFSHIN ANDREAS.Solar position algorithm for solar radiation applications[J].Solar Energy,2004,76(5):577-589.
[10]ROBERTO GRENA.An algorithm for the computation of the solar position[J].Solar Energy,2008,82(5):462-470.
[11]崔映红,卑振华.抛物面槽式太阳能集热器热力性能研究[J].华北电力大学学报:自然科学版,2010(3):49-54,63. CUI Yinghong,BEI Zhenhua.Research on the thermal performance of the solar parabolic trough collectors[J]. Journal of North China electric Power University:Natural Science Edition,2010(3):49-54,63(in Chinese).
[12]徐文鹏.计算机图形学[M].北京:机械工业出版社,2009.
[13]卞新高,杨缝缝,辛秋霞.一种大范围太阳光线自动跟踪方法[J].太阳能学报,2010(10):1298-1303. BIAN Xingao,YANG Fengfeng,XIN Qiuxia.An automatic sun-trackingmethod in 1arge range[J].Acta Energiae Solaris Sinica,2010(10):1298-1303(in Chinese).
A Sun-Tracking Error Compensation Method of Solar Parabolic Trough Concentrator
WANG Rui1,2,BIAN Xingao1,2
(1.College of Mechanical&electrical Engineering,Hohai University,Changzhou 213022,Jiangsu,China;
2.Nantong Ocean Research and Offshore Engineering Institute of Hohai University,Nantong 226019,Jiangsu,China)
In order to offset the detrimental effect of the deviation of the solar parabolic trough concentrator’s rotation axis on the sun tracking accuracy,this paper,taking a solar parabolic trough concentrator installed in the south-north direction as an example,through analyzing the position deviation of the solar parabolic trough concentrator’s rotary shaft after installation or 1ong-term operation,establishes a mathematical model of the rotary shaft deviation from the ideal position,develops the calculation formula for the sun elevation angle and azimuth angle relative to the rotary shaft,and compensates the error from the rotary shaft deviation.In addition,the algorithm mentioned in this paper is applicable to the tracking angle calculation of solar parabolic trough concentrator installed in the arbitrary direction.
2015-04-20。
王 锐(1990),男,硕士研究生,研究方向为太阳跟踪技术。
(编辑 董小兵)
国家重点基础研究发展计划(973计划)(2010CB 227102)。
Fund Project:the National Basic Research Program of China(973 Program)(2010CB227102).
1674-3814(2015)08-0083-05
TK513.4
A
KEY W0RDS:solarparabolictrough concentrator; suntracking;elevation angle;azimuth angle;tracking error;error compensation
