数控立铣加工稳定性Lobe图计算方法研究

数控立铣加工稳定性Lobe图计算方法研究*

孙新国1，桂林2

(1.南阳理工学院 机械与汽车工程学院，河南 南阳473004; 2.河南工业职业技术学院 汽车工程系，河南 南阳473000)

摘要：以立式数控铣床为研究对象，以刀尖频响函数预测模型和立铣切削过程动力学模型为基础，建立了立铣切削过程的动力学模型，得到了立铣切削过程稳定性Lobe图解析算法，计算出了立铣切削过程稳定性Lobe图。通过实验和预测稳定性Lobe图，得到他们的图形总体趋势一致，说明根据预测稳定性Lobe图选择切削参数，可以保证切削过程的稳定性。为研究主轴-刀柄结合面参数、刀柄-刀具结合面参数、刀具直径、刀具悬伸长度、切入角、切出角、切向切削系数以及径向切削系数等因素对稳定性Lobe图的影响提供了一种计算方法。

关键词：数控立铣；Lobe图；计算；加工稳定性

文章编号：1001-2265(2015)09-0140-03

收稿日期：2014-12-19；修回日期：2015-01-19

基金项目：*河南省科技厅重点攻关项目(112102210097)

作者简介：孙新国 (1979—)，男，河南南阳人，南阳理工学院讲师，硕士研究生，主要从事数控技术及应用方面的研究，(E-mail)xinguo5677@163.com。

中图分类号：TH166;TG506

Calculation Method Research of Cutting stability Lobe Graph for Vertical CNC Milling Machine

SUN Xin-guo1，GUI Lin2

(1.School of Mechanical and Automotive Engineering, Nanyang Institute of Technology, Nanyang Henan, 473004,China; 2.Department of Automotive Engineering, Henan Polytechnic Institute, Nanyang Henan 473000,China)

Abstract：Taking the vertical numerical control milling machine as the research object, it is based on the frequency response function for prediction model and dynamic model of milling process, and it is established for the dynamic model of milling process. It is obtained for the milling process stability of Lobe chart parsing algorithm. It is calculated for the milling process stability of Lobe diagram. Through the experiment and forecast for the stability of Lobe diagram, consistentoverall trend of their graphics is consistent. According to the selection of cutting parameter sprediction of stability of Lobe diagram, it is guaranteed for the stability of cutting process.It provides a calculation method for main research-handle with surface parameters, the tool joint parameters, tool diameter, the tool overhang length, angle, cutting angle, cutting coefficients and the radial cutting coefficient and other factors on the stability of Lobe graph.

Key words： vertical CNC milling; lobe graph; calculation; cuttingstability

0引言

数控立铣加工过程中，由于不连续切削，动态切削力周期性地激发刀具和工件相对振动，导致再生颤振。颤振不但影响加工质量、机床和刀具寿命，还可能给生产带来危险。因此，对加工稳定性进行预测非常重要[1-3]。为了提高数控立铣加工过程的稳定性，通常利用稳定性Lobe图来确定切削过程中稳定和不稳定的切削区域[4-7]。目前已经提出了很多稳定性计算的方法，包括数值法、解析法等。Smith等提出了一种基于铣削过程颤振时域仿真来绘制稳定性叶瓣图的方法，Altintas提出了一种利用零级傅里叶级数估计切削力的频域解析法来绘制稳定性叶瓣图的方法。尽管他们已经取得了一定的成果，但是稳定性Lobe图的计算方法还有必要进一步研究。

因此，以立式数控铣床为研究对象，以刀尖频响函数预测模型和立铣切削过程动力学模型为基础，对数控立铣加工稳定性Lobe图计算方法的研究有着十分重要的意义。

1建立立铣切削过程动力学模型

要建立立铣切削过程动力学模型，首先假设工件系统刚度远大于刀具系统[8-11]，即假设工件系统为刚性系统，考虑铣削加工过程中进给方向和法向两个自由度所建立的动态铣削模型如图1所示。

图1　动态铣削模型

建立机床-主轴-刀具系统，x轴和y轴方向的动力学方程可以表示为：

(1)

其中：

mx、my——分别为切削系统在x、y轴方向的质量；

cx、cy——分别为切削系统在x、y轴方向的阻尼；

kx、ky——分别为切削系统在x、y轴方向的刚度；

Fxj、Fyj——分别为作用在刀齿j上x、y轴方向的切削力分量；

Fx、Fy——分别为作用在切削系统上的总切削力在x、y轴方向的分量。

在数控立铣切削过程中，切削力会引起刀具和工件系统振动，并在工件表面产生振纹。动态切削厚度hj(t)主要由两部分组成：进给运动引起的静态部分hsj(t)=ftsinΦj，其中，ft为每齿进给率，Φj=Ωt；刀具位移引起的动态部分qd,j(t)。由于静态部分不会影响再生振动的动态切削厚度，所以，将瞬时动态切削厚度表示如下：

(2)

其中：

(3)

式中，T=2π/(NΩ)为刀齿周期，δj(t)为单位阶跃函数，用于确定刀齿是否在切削中。根据切削力理论，作用在刀齿j上的切向和径向切削力与轴向切深及切削厚度有关，表达式分别如下：

(4)

Kt和Kr分别为切向和径向切削力系数，a为切削深度。将上式切削力在x和y轴方向分解，可得：

(5)

将作用在每个刀齿上的切削力进行累加，可得作用在切削系统上的总切削力为：

(6)

将上式表示成矩阵形式可得：

(7)

将式(7)写成矩阵形式，可得：

(8)

可以看出，定向因子[A(t)]随时间变化，这也是车削过程和铣削加工的本质区别。铣削过程中，切削力以刀齿周期T=2π/(NΩ)为周期，因此，对此周期系统进行Fourier级数展开，并保留直流分量，可得：

(9)

因此，可得铣削过程动态切削力表达式如下所示：

(10)

2Lobe图解析算法

假定刀具与工件接触区的传递函数矩阵为：

(11)

上式中，Gxx(iω)和Gyy(iω)分别为x轴和y轴方向的直接频响函数；Gxy(iω)和Gyx(iω)分别为交叉频响函数。假定当前时刻t和前一个刀齿切削周期(t-T)的振动矢量如下所示：

(12)

根据谐波函数，颤振频率ωc处的振动可以描述为：

(13)

那么再生位移为：

{Δ(iωc)}={r(iωc)}-{r0(iωc)}=

(14)

因而可得出简化后的特征方程为：

(15)

(16)

因而，可得轴向切深临界值为：

(17)

通过求解，可得主轴转速为：

(18)

其中，k为叶瓣数。

通过上述分析，利用本研究提出的方法可以预测机床刀尖频响函数，根据所选的刀具、工件和切削过程径向接触角，获取动态切削系数。按照上述公式分别计算特征值、临界轴向切深及对应的主轴转速，在颤振发生频率范围内重复以上过程，可得到颤振稳定性Lobe图。

3Lobe图计算

通过解析方法绘制稳定性Lobe图，可以通过以下步骤实现：

(1)通过本研究提出预测方法，获取机床刀尖频响函数；

(2)在刀尖频响函数中，选择主模态附近的颤振频率；

(3)求解动态铣削系统的特征值；

(4)计算对应的主轴转速及临界切深；

(5)在设定的颤振频率范围内，重复上述过程。

通过以单模态立铣切削过程为研究对象，利用MATLAB实现稳定性Lobe图的计算，其伪代码如下：

inputKr,Kt,N,Φst,Φex；

input count,a,b；

loadGxx(iωc),Gyy(iωc)；

αxx=quad(myfun1，φst，φex)；

αxy=quad(myfun2，φst，φex)；

αyx=quad(myfun3，φst，φex)；

αyy=quad(myfun4，φst，φex)；

a0=Gxx(iωc)Gyy(iωc)(αxxαyyαxyαyx)；

a1=αxxGxx(iωc)+αyyGyy(iωc)；

fork=0:m

fori=1:count

ifreal(Λ)<0

κ=imag(Λ)/real(Λ)；

alim=-2πreal(Λ)(1+κ2)/(NKt)；

tt++；

n(tt)=60/(N((2k+1)π-2arctanκ))；

ap(tt)=alim；

end

end

end

plot(n,ap)；

切削刀具的刀齿数为2，切削条件如表1所示。

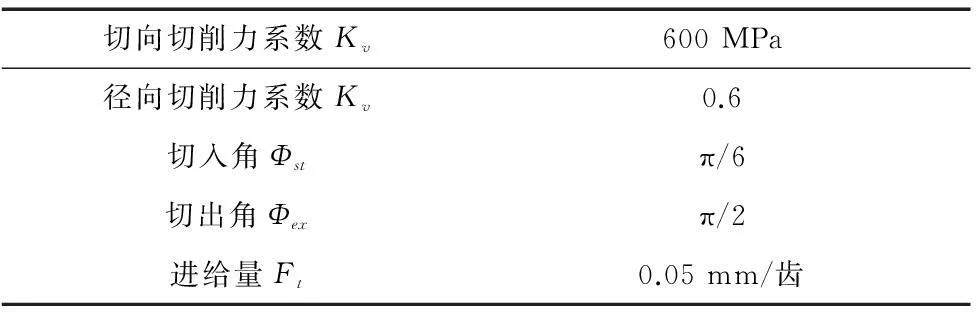
表1　加工过程稳定性分析切削条件

机床刀尖频响函数Gxx(iwc)和Gyy(iwc)可由预测方法得到，也可以通过锤击实验获取，分别基于实验和预测刀尖频响函数，绘制稳定性Lobe图，结果如图2所示。

图2　基于实验和预测刀尖频响函数稳定性Lobe图

4结论

从图2得到的稳定性Lobe图可以看出，实验和预测稳定性Lobe图总体趋势一致，但在主轴转速一定的前提下，预测极限切深小于实验极限切深。说明，根据预测稳定性Lobe图选择切削参数，可以保证切削过程的稳定性，但轴向切深选择有些保守，会在一定程度上影响加工效率。基于本研究提出的稳定性Lobe图计算方法，可以研究各个结合面对稳定性Lobe图的影响，并为数控机床的结构设计以及切削参数的选择打下坚实基础。

[参考文献]

[1] 杨建中，李江威，屈文晓，等．铣削加工过程稳定性分析[J]．中国机械工程， 2013，24(3)：360-365.

[2] 王清洁，李超，温强，等．组合算法在金属切削力预测中的应用[J]．组合机床与自动化加工技术，2013 (12)：14-15.

[3] 黎忠炎，高东强，毛志云,等．基于切削参数的高速铣削系统稳定性研究[J]．组合机床与自动化加工技术，2010(11)：16-18.

[4] 李志清．基于MATLAB 遗传算法的高速轴动力稳定性的优化设计[J]．煤矿机械，2012，33(4)：38-40.

[5] 孙国立，杨晓钧．Stewart型并联机构的振动建模与分析[J]．组合机床与自动化加工技术，2013(12)：4-10.

[6] 毛宽民，黄小磊，田红亮,等．机床固定结合面参数识别及其拟合方法[J]．华中科技大学学报(自然科学版)，2011，39(3)：18-21.

[7] 胡蒲希，钱炜，陈靖菲．基于直线电机伺服系统的数控铣削自适应控制系统的数学建模[J]．科学技术与工程，2011, 11(4)：838-840.

[8] 袁国伟．孔加工质量及高速钻削过程稳定性分析[J]．煤矿机械，2012，33(11)：127-128.

[9] 刘传伦，张胜文，朱成顺．双横梁高速龙门铣床的静动态特性分析研究[J].组合机床与自动化加工技术，2013(12)：37-40.

[10] 丛春晓，刘恒，吕凯波,等．细长轴切削的非线性系统动力稳定性分析[J]．组合机床与自动化加工技术，2011(10)：40-44.

[11] 张强，尹志宏，张明旭,等．基于ANSYS Workbench的大型数控龙门铣镗床床身静动态特性分析[J]．科学技术与工程，2012,12(1)：180-183.

(编辑李秀敏)