含水率对山核桃树木材应力波频谱的影响

靳守领，杜晓晨*，冯海林,3，方益明，王再超

（1. 浙江农林大学信息工程学院，浙江 临安 311300；2. 浙江省林业智能监测与信息技术研究重点实验室，浙江 临安 311300；3. 通信网信息传输与分发技术重点实验室，河北 石家庄 050081）

含水率对山核桃树木材应力波频谱的影响

靳守领1,2，杜晓晨1,2*，冯海林1,2,3，方益明1,2，王再超1,2

（1. 浙江农林大学信息工程学院，浙江 临安 311300；2. 浙江省林业智能监测与信息技术研究重点实验室，浙江 临安 311300；3. 通信网信息传输与分发技术重点实验室，河北 石家庄 050081）

对5组山核桃（Carya cathayensis）木材健康试样和5组腐朽试样在不同含水率下的应力波频谱进行测试，分析应力波频谱中共振频率随含水率的变化规律。结果表明：含水率是影响木材中应力波频谱的重要因素，应力波频谱中的共振频率随含水率的增加呈逐渐下降趋势，在含水率低于纤维饱和点时，应力波频谱中共振频率随含水率下降幅度相对较大，反之则较小，且对高频部分共振频率的影响比低频部分共振频率较大；健康和腐巧两种试材含水率与应力波频谱中共振频率之间的线性回归模型拟合优度较高，相关系数R2均高于0.93。

应力波频谱；共振频率；含水率；山核桃树

基于频谱分析技术的木材无损检测已成为充分有效利用森林和木材资源的重要手段之一，该技术具有简单、快速、准确等特点[1~2]，能够用于检测立木原木及木结构构件内部腐朽和空洞。杨慧敏、王立海先后研究了基于超声波频谱和超声波功率谱分析技术在木材孔洞缺陷无损检测中的应用[3~4]，并取得了较好的效果。余观夏等人也提出了在频域内采用应力波频谱分析技术检测原木腐朽的方法，根据应力波频谱中的共振频率来判断木材的健康状况，该方法能够判断木材中的缺陷类型，精度较高，具有较高的实用价值[5~6]。

然而，木材是一种各向异性材料，结构极其复杂，故而应力波在木材内部的传播过程是一个较为复杂的过程，受到多种因素的共同影响。研究结果表明：含水率对木材动态弹性模量影响显著[7~8]，而木材的动态弹性模量直接关系到传播过程中应力波频谱的共振频率[9~11]。在实验过程中，同样发现应力波频谱中的共振频率受含水率的影响较大。因此，含水率是影响木材中应力波频谱的一个重要因素。

在森林作业和木材加工时，环境湿度和木材的含水率变化较大，为了能够采用应力波频谱分析技术对立木及原木的力学性质和内部缺陷进行及时有效地评估，非常有必要研究含水率对应力波在木材中传播时频谱的影响。

本试验针对5组山核桃树健康试样和5组山核桃树腐朽试样，研究含水率对木材中应力波频谱的影响，力求找到应力波频谱随含水率变化的规律，为采用应力波频谱检测技术评估立木及原木等提供基本技术参数。

1 材料与方法

1.1 实验材料

选用健康的山核桃树和腐朽的山核桃木材作为实验的木材试样，试样规格：试件直径363 mm，厚度120 mm，健康的山核桃树木材试样数量5个，分别计为1号、2号、3号、4号和5号试件；腐朽的山核桃木材试样数量5个，分别计为6号、7号、8号、9号和10号试件，其中1号木材试样和6号木材试样如图1。

1.2 实验设备

实验中主要用到以下3种设备：秦皇岛北戴河兰德公司生产的BZ11系列加速度传感器，用于接收试件中的应力波信号；美国 Tektronix公司生产的TDS2000系列 2022数字示波器，用于显示并存储实验中接收到的信号；KT-R重锤式木材测湿仪，用于快速测定试件的含水率，测量含水率范围3.5% ~ 99.9%，能够调节温度和木材试样密度进行校正。

1.3 实验方法

本文主要研究含水率对木材中应力波频谱的影响，假设木材试样横截面在振动中始终保持为平面，仅考虑一条直径上的应力波，略去该直径在纵向振动中的横向变形[12]。由此根据机械振动理论可以列出其振动方程，解之可得到多个固有频谱[9,11]。由于这些固有频率，在木材受到激励时，木材会产生共振，在应力波频域内出现多个共振频率，如图2。

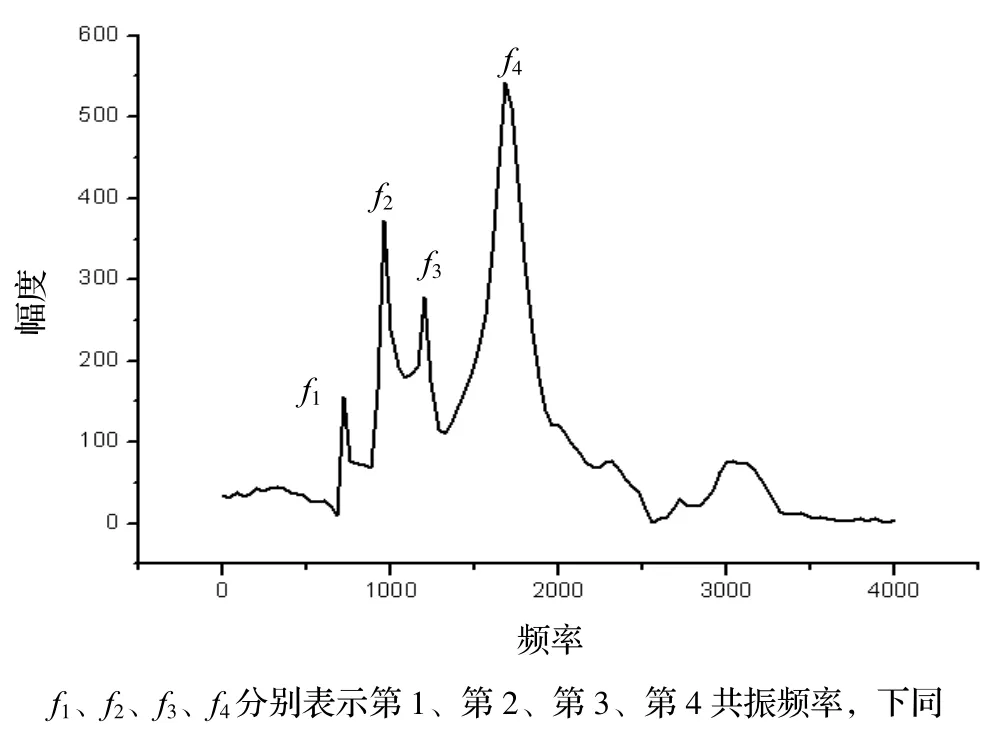
图2 应力波频谱图Figure 2 Stress wave spectrum

这些固有频率在数值上等于机械振动中的共振频率，频谱中这些共振频率是由木材微观结构的复杂性决定的，同时也反映了木材本身性质的各向异性或者腐朽的各向异性[5]。

在常温状态下，将10组木材试样放入水中进行浸泡，以提高其含水率。48 h后，将木材试样取出。木材试样中水分达到饱和。在10组木材试样的横截面上分别画出一条穿过圆心的直线，用KT-R重锤式木材测湿仪在每条直线上依次测定每个试件的含水率，并计算其平均值（本文中测定8个点的含水率，并求其平均值作为实验参数）。

在每条直线的两端安装加速度传感器（图 3）。在每条直线一端用力锤敲击激励传感器，将接收传感器收到的应力波信号传给数字示波器，用TDS2022数字示波器配套的软件进行采集信号，减小人为误差。

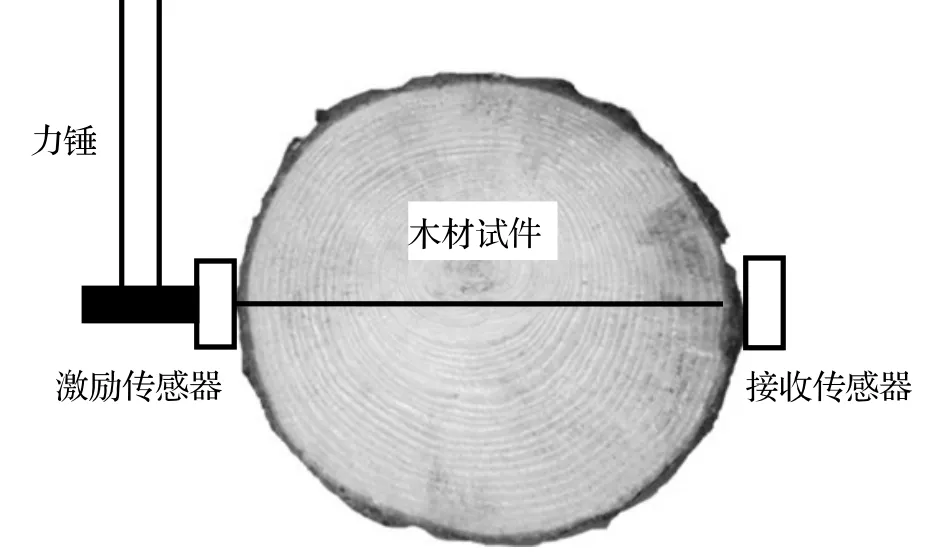
图3 传感器分布示意图Figure 3 Sensor position

应力波信号采集时，在相同条件下，敲击激励传感器，敲击次数为5次，取应力波频谱中共振频率的平均值参与分析，以减少实验误差。将试件做干燥处理，含水率每出现变化，依据上述方法，对10组木材试样依次进行测试，可得到不同含水率下的应力波信号。对采集到的应力波信号采用matlab进行小波降噪处理，然后进行FFT变换，并记录频域中的共振频率。

2 结果与分析

2.1 应力波频谱随含水率的变化规律

将10组应力波频谱中的共振频率进行汇总，得到5组健康木材试样和5组腐朽木材试样不同含水率时，应力波频谱中共振频率随着含水率变化的曲线。由图4可知，虽然木材试样不同，试样的健康状况也不同，但10组木材试样应力波频谱中共振频率随含水率的变化规律具有高度的一致性。

从图4可知，无论木材是健康还是腐朽，不同含水率时，含水率变化对应力波频谱中共振频率的影响具有相似性，即随着木材含水率的增加，应力波频谱中的共振频率均有下降趋势。

其中在健康木材试样中含水率低于33.6%，在腐朽木材试样中含水率低于32.1%时，应力波频谱中共振频率减小较快，下降幅度相对较大；而在健康木材试样中含水率高于 33.6%，在腐朽木材试样中含水率高于 32.1%时，应力波频谱中共振频率下降趋势变得较为平缓。这主要是由于健康的核桃树样本和腐朽山核桃树样本的木材纤维饱和点分别在含水率33.6%和32.1%附近。

木材的纤维饱和点是木材物理力学性质改变的一个重要分界点[14~15]，其值随树种和材质而异。在纤维饱和点以上，木材细胞壁中结合的水分已经饱和，水分以自由水的形式存在于细胞腔中[15]，水分对木材性质的影响逐渐降低，此时，木材如受到干燥或受潮，只是自由水改变，故不会引起湿胀干缩；在纤维饱和点以下，木材中的水分仅存在于细胞壁中，此时，木材如收到干燥或受潮，则能引起木材的湿胀干缩，对木材的性质具有较大的影响。

通过以上分析可知：以木材的纤维饱和点为界，含水率在纤维饱和点以上，应力波频谱中共振频率随着含水率变化下降趋势平缓；而在纤维饱和点以下，应力波频谱中共振频率随含水率变化下降幅度较大；无论是在纤维饱和点以上，还是在纤维饱和点以下，当含水率增大时，高频部分的共振频率下降幅度均比低频部分大，即含水率对木材中应力波频谱高频部分的影响比低频部分更加剧烈。应力波频谱中共振频率随含水率的变化规律与木材是否存在腐朽无关。

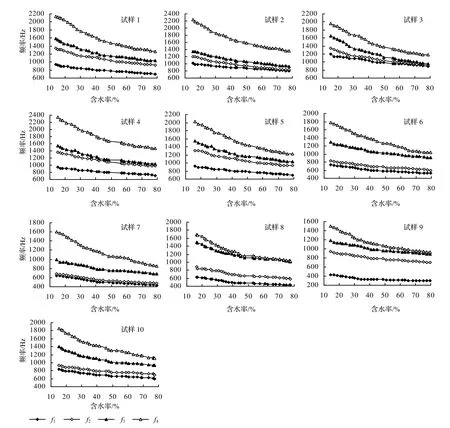
图4 木材试样中不同含水率对应力波频谱的影响Figure 4 Effects of moisture content on stress wave spectrum

2.2 含水率与应力波频中共振频率的回归模型

为找到含水率与应力波频谱中共振频率之间更为具体的关系，对不同含水率时所测得的应力波频谱数据用OriginPro 8软件进行线性拟合，图5为1号木材试样和6号木材试样以纤维饱和点附近为分界，各个共振频率与含水率关系的线性拟合图。

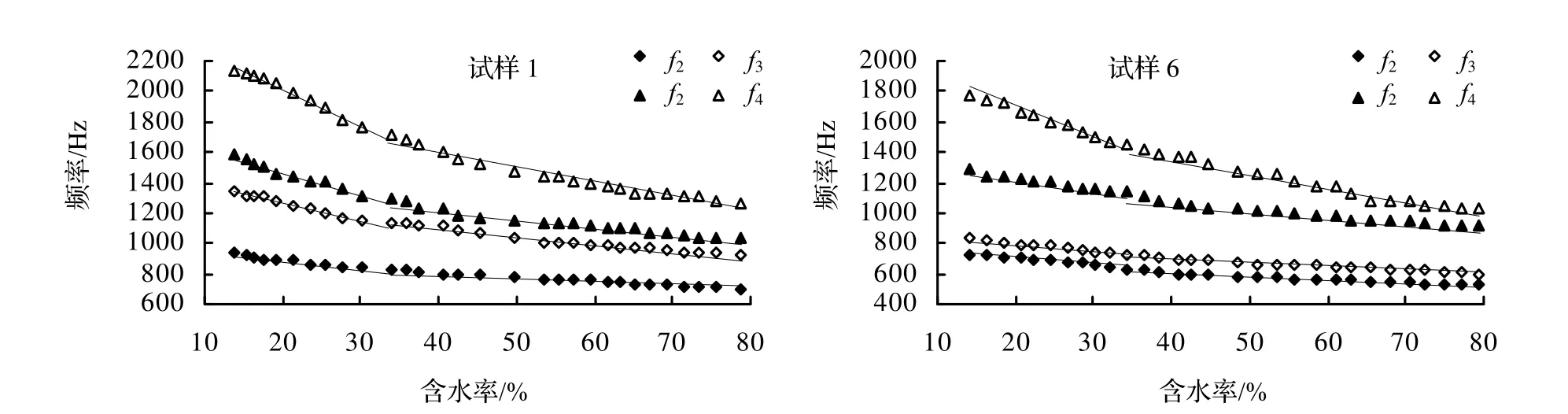
图5 木材试样含水率对山核桃树中应力波频谱各个共振频率的关系拟合Figure 5 Linear fitting of moisture content and each resonant l frequency for the 1stand 6thspecimen

由图5可知，无论是高于先纤维饱和点和低于纤维饱和点，在健康木材试样和腐朽木材试样中各个共振频率随着含水率的增大而下降的趋势近似为一条直线。对不同含水率下所测得的应力波频谱数据进行线性回归分析，建立两者之间的回归模型，见表1。

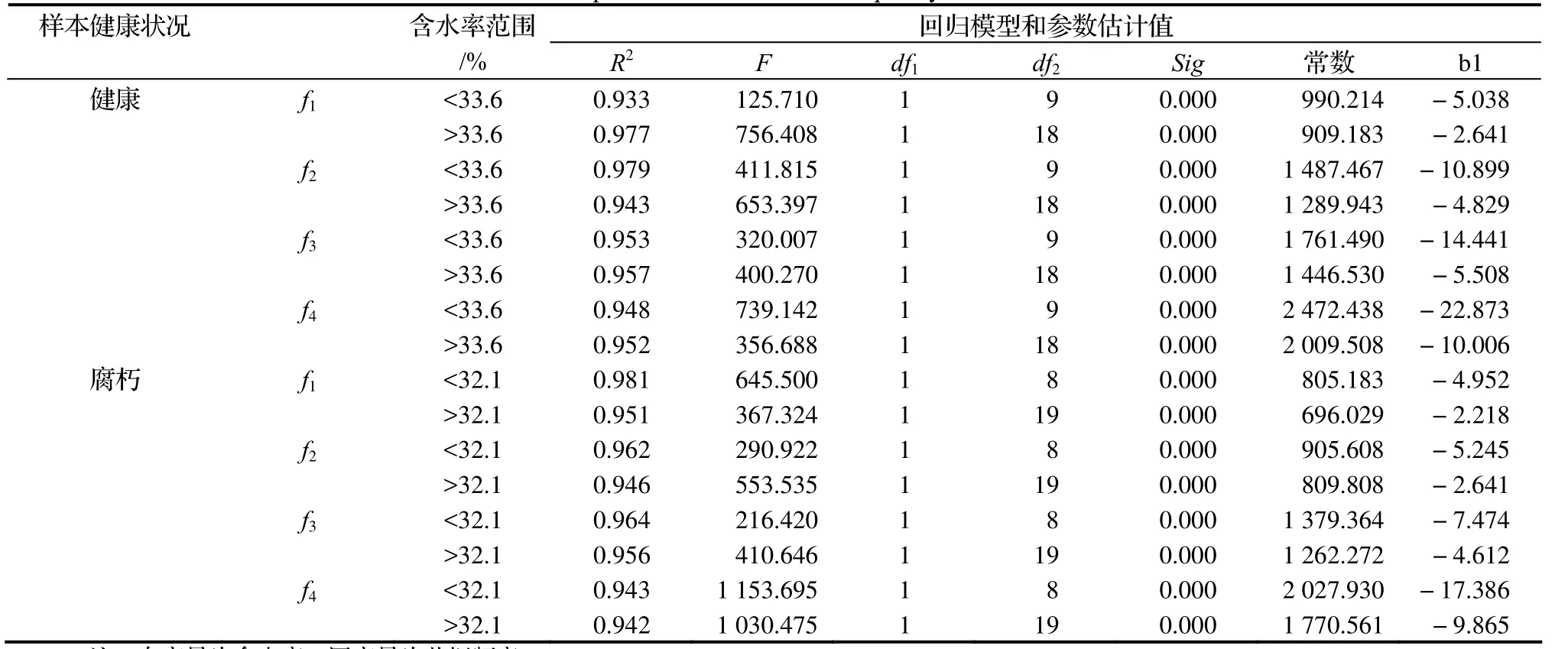
表1 木材中应力波频谱共振频率和不同含水率的线性模型和参数估计值汇总Table 1 Linear models and parameters for resonant frequency and different moisture content

由表1可知：以木材的纤维饱和点（本实验中健康木材试样约为33.6%，腐朽木材试样约为32.1%）为分界线，含水率与各个共振频率呈负相关的线性关系。所建立的线性回归模型，R2均高于0.93，回归模型具有较高的拟合优度，F检验置信度也都在0.001水平上。因此，可以通过回归模型对山核桃树在不同含水率下的应力波频谱中共振频率的变化进行估计。

3 结论

通过测试山核桃树健康试样和腐朽试样在不同含水率下的应力波频谱，分析了含水率对木材中应力波频谱共振频率的影响，并建立了两者的回归模型。分析得到以下结论：

（1）在不同含水率下，木材中应力波频谱共振频率随着含水率变化都具有相似的变化规律，即随着含水率的增加有逐渐下降的趋势。其中在含水率低于纤维饱和点时，应力波频谱中共振频率随含水率变化下降幅度较大；而在含水率高于纤维饱和点时，应力波频谱中共振频率随含水率变化下降趋势逐渐平缓，这种变化规律与木材是否存在腐朽无关。

（2）在不同含水率时，无论含水率在纤维饱和点以上，还是在纤维饱和点以下，相对来讲，健康试样和腐朽试样应力波频谱中共振频率高频部分与低频部分虽然具有一致的变化趋势，但是变化幅度并不相似，高频部分下降幅度明显比低频部分大，即含水率对木材中应力波频谱高频部分的影响比低频部分更加剧烈。

（3）根据健康和腐朽两种木材试样的数据所建立的含水率与应力波频谱共振频率之间的线性回归模型中，拟合优度较高，相关系数R2均在0.93以上。从该模型中也可看出，纤维饱和点是应力波频谱中共振峰变化规律的一个分界点。

[1] 于文勇，王立海，杨慧敏，等. 超声波木材缺陷检测若干问题的探讨[J]. 森林工程，2006，22（6）：7-9.

[2] 于鸣，任洪娥，常春媛. 木材强度无损检测的音频信号分析[J]. 木材加工机械，2006，17（3）：28-30.

[3] 杨慧敏，王立海. 基于超声波频谱分析技术的木材孔洞缺陷无损检测[J]. 东北林业大学学报，2007，35（8）：30-32.

[4] 杨慧敏，王立海. 超声波功率谱技术在木材空洞缺陷无损检测中应用[J]. 森林工程，2005，21（2）：8-9.

[5] 余观夏，张爱珍，史伯章，等. 用应力波频谱分析技术检测原木中的腐朽[J]. 东北林业大学学报，2007，35（10）：22-25.

[6] 张爱珍，于观夏，张训华. 以应力波频谱为特征的木材腐朽自动检测[J]. 木材加工机械，2010，21（4）：8-11.

[7] 司慧，鹿振友，王立昌. 含水率对落叶松材动态弹性模量的影响[J]. 木材加工机械，2007，18（1）：16-19.

[8] 赵雪松，俞国胜，朱建国，等. 不同含水率对四倍体刺槐抗弯强度及弹性模量的影响[J]. 河南农业科学，2013，42（5）：177-180.

[9] 张厚江，申世杰，崔英颖，等. 振动方式测定木材弹性模量[J]. 北京林业大学学报，2005，27（6）：91-94.

[10] Guntekin E，Emiroglu Z G，Yilmaz T. Prediction of Bending Properties for Turkish Red Pine（Pinus brutia Ten.) Lumber using Stress Wave Method[J]. BioResources，2012，8（1）：231-237.

[11] 管珣，赵茂程，王正，等. 基于纵向共振法测试杨树原木应力波波速及弹性模量的研究[J]. 西部林业科学，2013，42（2）：14-19.

[12] 冯海林，李光辉，方益明，等. 应力波传播模型及其在木材检测中的应用[J]. 系统仿真学报，2010，22（6）：1 490-1 493.

[13] 徐华东，王立海. 温度和含水率对红松木材中应力波传播速度的影响[J]. 林业科学，2011，47（9）：123-128.

[14] 徐世克，汤颖，章卫钢，等. 竹材介电性质研究[J]. 浙江林业科技，2012，32（6）：18-21.

[15] 李坚. 木材科学[M]. 北京：高等教育出版社，2002.

Effect of Moisture Content on Stress Wave Spectrum of Carya cathayensis Wood

JIN Shou-ling1,2，DU Xiao-chen1,2*，FENG Hai-lin1,2,3，FANG Yi-ming1,2，WANG Zai-chao1,2
（1. School of Information Engineering, Zhejiang A & F University, Lin’an 311300, China；2. Zhejiang Provincial Key Laboratory of Intelligent Monitoring in Forestry and Information Technology, Lin’an 311300, China；3. Science and Technolog y on Information Transmission and Dissemination in Communication Networks Laboratory, Shijiazhuang 055581, China）

Detection was conducted on stress wave of 5 clear and 5 decayed specimen of Carya cathayensis wood with different moisture content. Variation of detected stress wave spectrum was analyzed. The results showed that moisture content of the wood tested was an important factor affecting the stress wave spectrum. Resonant frequency of the stress wave decreased gradually with the increase of moisture content, and greatly with the moisture content below fiber saturation point. The regression model between stress wave spectrum and moisture content was established. The linear regression model between moisture content of the tested wood with resonant frequency in stress wave had high goodness of fit. The correlation coefficient (R2) was higher than 0.93.

stress wave spectrum; resonant frequency; moisture content; Carya cathayensis

S781.5

A

1001-3776（2015）01-0030-06

2014-02-24；

2014-06-11

国家自然科学基金项目（61272313, 61302185, 61472368）；浙江省科技厅公益性项目（2012C21015, 2013C31018, 2014C31044）；浙江省国际合作项目（2013C24026）；浙江省自然科学基金项目（LQ13F020013, LQ14F020014）；浙江省林业智能监测与信息技术研究重点实验室开放基金（100151402）；通信网信息传输与分发技术重点实验室开放课题（KX132600016 / ITD-U13009）

靳守领（1987-），男，河南安阳人，硕士生，从事木材无损检测研究；*通讯作者。