一种新型量子阱中三次谐波的研究

郭康贤，张仲敏

(广州大学物理与电子工程学院，广东广州 510006)

0 Introduction

In the past few years，many attentions have been focused on the nonlinear optical properties of low－dimensional semiconductor structures in both the theoretical and applied aspects.With the remarkable progress in nanofabrication techniques，it is now possible to produce low－dimensional semiconductor structures such as quantum dots，quantum wells，quantum wires and superlattices［1－10］.Due to the enhanced confinement in low－dimensional semiconductor structures，many novel optical properties appear in these structures.These properties are prospective to be applied to design advanced optical devices.

The nonlinear optical properties are studied by many researchers.Among the nonlinear optical properties，more attention has been paid to the THG coefficient.In 2005，YU，et al surveyed the polaron effects on the THG coefficients in cylindrical quantum－well wires［11］.Their results revealed that the THG coefficients are greatly enhanced and the peak shifts to the aspect of high energy when the influence of electron－phonon interaction is taken into considera－tion.In 2009，ZHANG，et al researched the thirdharmonic generation in cubical quantum dots［12］.Their results demonstrated that the THG strongly depends on the length of CQDs and the magnitude of the electric field.Also，the peaks shift towards the higher energy region with increasing electric field.In 2011，SHAO，et al investigated the third－harmonic generation in cylindrical quantum dots in a static magnetic field［13］.Their results showed that the THG coefficients can reach a magnitude of 10－10m2·V－2.In addition to the radiusRof the cylindrical quantum dots，both the parabolic confining potential and the static magnetic field have influences on the THG coefficients.In 2014，MOU，et al studied the THG coefficients in asymmetrical semi－exponential quantum wells［14］，their results showed that both the amount of peaks of THG coefficients and the magnitude of peaks are significantly affected by σ andU0.

This paper is organized as follows.We will theoretically study the THG coefficients in the system withU0tan2(πz/d)potential.In section 2，the eigenfunctions and the energy eigenvalues are obtained by solving Schrodinger equation.Then we get the analytical expression of the THG coefficients with the compact－density－matrix approach and iterative method.In section 3，numerical results and discussions are performed.In section 4，a brief conclusion is made.

1 Theory

In this paper，we assume an electron confined in quantum wells withU0tan2(πz/d)potential.Within the framework of effective－mass approximation，the Hamiltonian of the system can be expressed as follows:

where

In the equation，zdenotes the growth direction of the quantum well，h represents Planck constant，m*is the effective mass of electron in conduction band，U0is a parameter，dis width of the well.From the expression ofV(z)，we can find thatU0anddhave great influences on the potentialV(z).The influence is exhibited in Fig.1 and Fig.2.From Fig.1 it can be found that whenU0is the same，the value of bound potential decreases with the increment ofdat the same point of coordinate axisz.In contrast，from Fig.2 we can find that the magnitude of the bound potential increases with the increment ofU0whendremains unchanged.

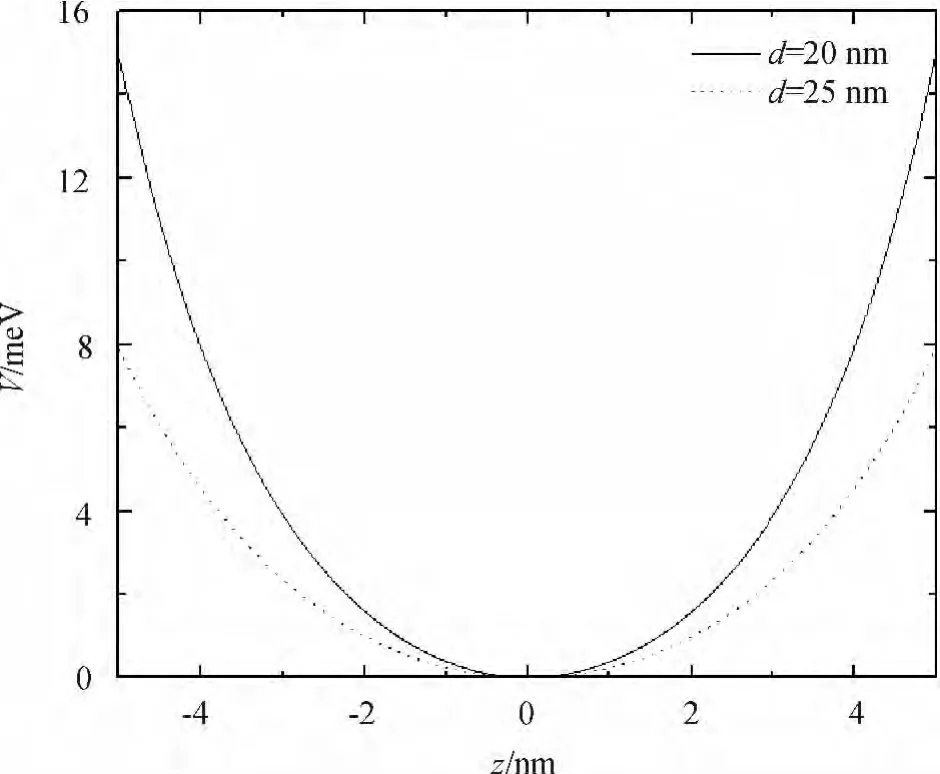
Fig.1 The potential V(z)as a function of z for two different values of d=20 nm and d=25 nm with U0=15 meV

Fig.2 The potential V(z)as a function of z for two different values of U0=15 meV and U0=25 meV with d=20 nm

The Schrödinger equation inzdirection has the following form:

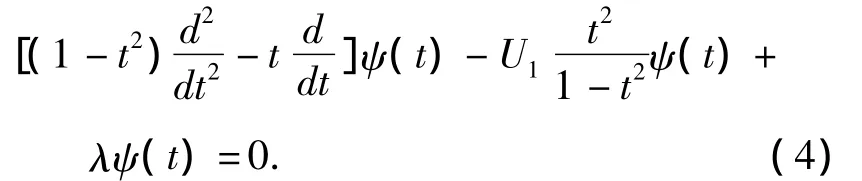
WhereU1By solving this equation，we can obtain energy spectrum

We can also get the wave function

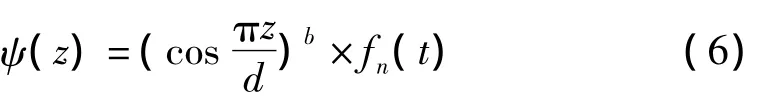
wheren=0，1，2，3…fn(t)can be written as:

whereb=

Suppose our system is excited by an electromagnetic field.The electric field vector of the applied electromagnetic field is

the evolution of the density matrix operator ρ is given by the following Liouville quantum equation［1，5，8］

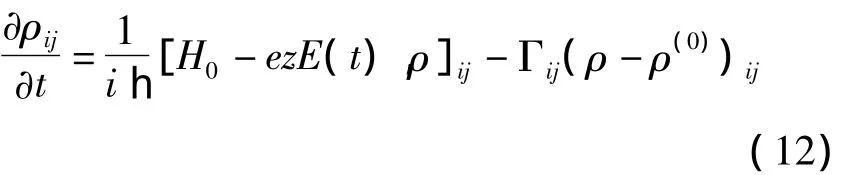
whereH0is the Hamiltonian of the system without the application of electromagnetic field(t)，ρ(0)is the unperturbed density matrix，and Γijis the phenomenological relaxation rate which arises from the interactions of the electron－phonon and electronelectron and other collision processes.In this paper we choose Γij= Γ0=wheni≠jfor simplification.Eq.(12)can be solved with iterative method［10－11］，

with［4，7］

The electronic polarization can be expanded as Eq.(13).Neglecting the terms which contribute little to our calculations，we can get a concise expression of the electronic polarization［12］.

where ε0is the vacuum permittivity，χ(1)ωandχ(3)ωare the linear and third order nonlinear susceptibility coefficients，respectively.The electronic polarization of the nthorder electronic polarization is given as［12－14］

whereSis the volume of interaction andTrdenotes the trace or summation over the diagonal elements of the matrix ρ(n)ez.By using the compact density matrix approach and the iterative procedure，the analytical expression of the THG coefficients for the system can be expressed as［11－12，14］:

where συis the electron density in the system，M01=＜ ψ0zψ1＞ ，M12= ＜ ψ1zψ2＞ ，M23= ＜ ψ2zψ3＞ andM30= ＜ ψ3zψ0＞ are the off－diagonal matrix elements，h ω10=E1－E0，h ω20=E2－E0，h ω30=E3－E0.

2 Results and discussions

We will discuss the THG coefficients in quantum wells withU0tan2(πz/d)potential.The parameters used in our calculations are as follows:m*=0.067m0(wherem0is the mass of free electron)，ε0=8.85×10－12Fm－1and συ=5.0×1022m－3.

In Fig.3，we draw THG coefficients as a function of incident photon frequency ω for three different values ofd=18 nm，d=20 nm andd=22 nm withU0=15 meV.In the figure，we can clearly find two characteristics.The first one is that the magnitude of peak for each curve increases with the augment of d.The second one is that the peaks of the THG coefficients exhibit a red shift whendincreases.These two characteristics can be explained in Fig.4 and Fig.5.

Fig.3 The THG coefficients as a function of the incident photon frequency for three different values of d=18 nm，d=20 nm and d=22 nm with U0=15 meV

Fig.4 The matrix elements'product M01M12M23M30as a function of d with U0=15 meV

Fig.5 The energy intervals E10，E20/2 and E30/3 as a function of d with U0=15 meV

In Fig.4，the matrix elements'product as function ofdwithU0=15 meV is depicted.The first characteristic is related to the product of matrix elements.In Fig.4，we can clearly find that the matrix elements'product increases with the increment ofd.The physical reason for this feature is that the overlaps between different electronic states become greater with increasingd.Therefore we can find the first characteristic.

In Fig.5，energy intervalsE10，E20/2 andE30/3 as a function ofdwithU0=15 meV is presented.The reason of the second characteristic is attributed to the diminution of energy intervals with increasingd.From Fig.5，we can find thatE10，E20/2 andE30/3 decrease with the increment ofd.This phenomenon is related to the fact that the confinement of the potential becomes weak whendincreases.So we can see the second characteristic.

In Fig.6，we plot THG coefficients versus incident photon frequency ω for three different values ofU0=5 meV，U0=15 meV andU0=25 meV withd=20 nm.We can find that the peak of THG coefficients decreases with the increasingU0.This characteristic is due to the fact that the product of matrix elements decreases with the increasingU0，in which we can clearly find this trait in Fig.7.Moreover，we can also find that the peaks of THG coefficients display a blue shift whenU0increases.This trait can be explained in Fig.8.

Fig.6 The THG coefficients as a function of the incident photon frequency for three different values of U0=5 meV，U0=15 meV and U0=25 meV with d=20 nm.

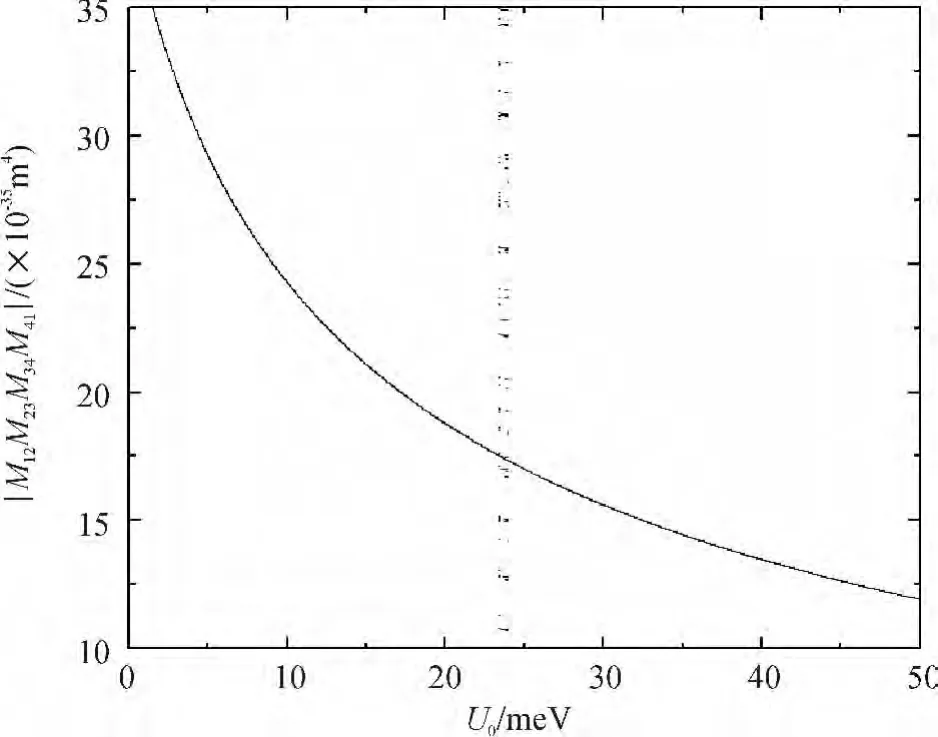
Fig.7 The matrix elements'product M01M12M23M30as a function of U0with d=20 nm

In Fig.7，the product of matrix elements as function ofU0withd=20 nm is displayed.We can find that the product of matrix elements diminishes whenU0increases.The physical reason for this feature is that the overlaps between different electronic states decrease whenU0increases.This is the reason for the fact that the peak of THG coefficients decreases with the increasingU0.

Fig.8 The energy intervals E10，E20/2 and E30/3 as a function of U0with d=20 nm.

In Fig.8，we plot energy intervalsE10，E20/2 andE30/3 versusU0withd=20 nm，we can find thatE10，E20/2 andE30/3 increase with the augment ofU0.The physical reason for this feature is that the confinement of the potential is enhanced whenU0increases.This is why the peaks of THG coefficients display a blue shift whenU0increases.

3 Conclusion

In this paper，we have obtained the eigenfunctions and energy eigenvalues through solving Schrodinger equation.Then the analytic expression of the THG coefficients is derived.Numerical calculations show that the THG coefficients are strongly affected bydandU0.In the end，we hope that our results obtained in our research will helpfully contribute to the advance in the field of nonlinear optics.

［1］ GUO K X，GU S W.Nonlinear optical rectification in parabolic quantum wells with an applied electric field［J］.Phys Rev B，1993，47:16322－16325.

［2］ WANG G H.Third－harmonic generation in cylindrical parabolic quantum wires with an applied electric field［J］.Phys Rev B，2005，72:155329－155334.

［3］ ZHANG L.Electric field effect on the linear and nonlinear intersubband refractive index changes in asymmetrical semiparabolic and symmetrical parabolic quantum wells［J］.Superlatt Microstr，2005，37:261－272.

［4］ YU Y B，ZHU S N，GUO K X.Electron－phonon interaction effect on optical absorption in cylindrical quantum wires［J］.Solid Stat Commun，2006，139:76－79.

［5］ ROBERT B.Nonlinear optics［M］.2nd ed.New York:Academic Press，2003.

［6］ KASAPOGLU E，SARI H，SOKMEN I.Intersubband optical absorption in a quantum well under a tilted magnetic field［J］.Superlat Microstr，2001，29:25－32.

［7］ CHEN B，GUO K X，WANG R Z，et al.Linear and nonlinear intersubband optical absorption in double triangular quantum wells［J］.Solid Stat Commun，2009，149:310－314.

［8］ PRASAD V，SILOTIA P.Effect of laser radiation on optical properties of disk shaped quantum dot in magnetic fields［J］.Phys Let A，2011，375:3910－3915.

［9］ YESILGUL U，SAKIROLU S，KASAPOGLU E，et al.Hydrogenic impurities in quantum dots under intense high－frequency laser field［J］.Phys B，2011，406:1441－1444.

［10］ SADEGHI E.Electric field and impurity effects on optical property of a three dimensional quantum dot:A combinational potential scheme［J］.Superlat Microstr，2011，50:331－339.

［11］ YU Y B，ZHU S N，GUO K X.Polaron effects on third－harmonic generation in cylindrical quantum－well wires［J］.Solid Stat Commun，2004，132:689－692.

［12］ ZHANG Z H，GUO K X，CHEN B，et al.Third－harmonic generation in cubical quantum dots［J］.Superlatt Microstr，2009，46:672－678.

［13］ SHAO S，GUO K X，ZHANG Z H，et al.Third－harmonic generation in cylindrical quantum dots in a static magnetic field［J］.Solid Stat Commun，2011，151:289－292.

［14］ MOU S，GUO K X，XIAO B.Studies on the third－harmonic generation coefficients in asymmetrical semi－exponential quantum wells［J］.Superlat Microstr，2014，65:309－318.