基于区间数回归模型的未决赔款准备金评估

冯卫泽，王达布希拉图

(广州大学a.数学与信息科学学院;b.经济与统计学院;c.岭南统计研究中心，广东广州 510006)

众所周知，在非寿险中未决赔款准备金是针对案发已记录的但还未完全理赔的保险风险所预留的准备金.由于缺乏类似寿险生命表的完整的保险标的损失分布表，导致未决赔款准备金评估远比寿险中的准备金计算复杂.目前，人们针对未决赔款准备金的估算提出了链梯法、案均赔款法、准备金进展法、B－F法等，其大致可分为确定性方法和随机性方法.前者估算的结果是一确定的数，后者估计出来的未来未决赔款准备金不是一个准确值，而是一个变量.随机的方法相对于确定性的方法具有明显的优点，例如，随机的方法可对假设的模型进行诊断，并可给出估计值的置信区间.KREMER［1］提出对数正态模型，结合了对数正态分布理论估计未决赔款准备金.MACK［2］对KREMER的模型进行部分改进，将赔款额看做一个服从伽马分布的随机变量，给出未决赔款准备金的伽马模型.SHERMAN［3］给出指数型平滑发展因子模型.RENSHAW等［4］结合广义线性模型，运用准极大似然估计方法进行参数估计.这种方法有助于处理赔款增量出现负值的问题.孟生旺［5］在假设增量赔款服从指数分布族的条件下，应用广义线性模型评估未决赔款准备金.卢志义等［6］分析利率厘定和准备金估计中广义线性模型的建模方法，指出数据缺失和数据质量较低是导致传统模型估计结果欠佳的原因.陈迪红等［7］通过状态空间来描述非寿险赔付过程，应用卡尔曼滤波来估计状态空间的转换参数，并分别预测损失频率和损失程度，从而动态地估计未决赔款准备金.SÁNCHEZ［8］结合模糊回归理论，利用模糊回归方法评估未决赔款准备金.这种方法比较适合于数据信息欠清晰的情形，但有时评估的计算量偏大.考虑到区间数界限分明、信息含量丰富的优点，本文在链梯法的指数平滑型进展因子基础上，利用区间数回归方法估计各发展年间的进展因子，给出一种新的未决准备金的评估方法.

1 预备知识

1.1 区间数的定义及其运算

定义1A=［a，b］={x:a≤x≤b}称为一个区间数，a和b分别称为区间数的下限(左端点)和上限(右端点).当a=b时，区间数退化为一个实数.区间数的全体记为I(R).区间数还可以表示成另一种形式:A=＜c(A)，r(A)＞.其中c(A)=)表示的是A的中点，也可称为A的位置系数，反映了A的大小;r(A)=表示的是A的半径，也可称为A的不确定系数，反映了A的不确定程度.

定义2 称n个有序区间数组X=(X1，X2，…，Xn)为n维区间向量，其中Xi∈I(ℜ)，i=1，2，…，n.n维区间向量的全体记为I(ℜn).

定义3 对于任意X1，X2∈I(ℜ)，X1=［，］，X2=［x2］，都有如下的运算关系:，其中0 ∉［x2］.

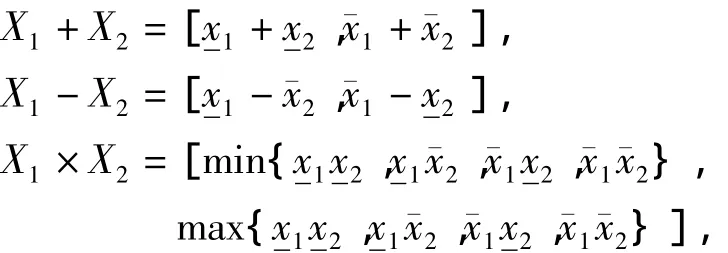
定义4 设存在X∈I(ℜ)，X=［］.另外对于任意实数λ∈R有

1.2 区间数据的线性回归方法

2000年BILLARD等［9］提出区间数据的线性回归模型的 CM 方法.之后，NETO 等［10－11］对 CM方法进行改进，提出CRM和CCRM的方法来拟合区间线性回归方程.然而，上述模型的自变量和因变量都是区间数.本文考虑自变量是精确值，而因变量是区间数的情况.

设有一个区间变量Y和P个实变量Xj，j=1，2，…，p，yi=［yi］，表示的是区间变量Y的第i次观测值，xij=［xij］表示的是实变量Xj的第i次观测值，i=1，2，…，n.则所有的样本可以表示为如下的矩阵形式:

考虑如下形式的线性回归方程:

其中，［βi］=［βi］，i=1，2，…，p是待估计系数，［，］是误差项.若将区间数等价地表示成中心和半径的形式，即［Y］= ＜c［Y］，r［Y］＞，［βi］=＜c［βi］，r［βi］＞，［ε］= ＜c［ε］，r［ε］＞.那么，上述方程可以转化成下面两个线性回归方程:

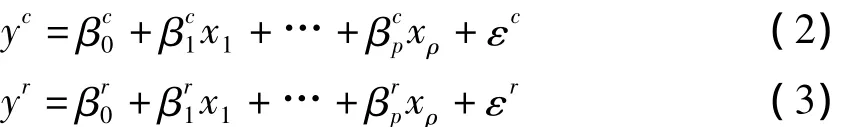
因此，［Y］的预测值可以写成［］=［，］，其中=－

1.3 链梯法［12］

链梯法依赖每年的赔付数据，并用流量三角形形式将这些数据加以表述，见表1.Cij表示事故发生在第i年，而在第i+j年的赔付额.可将表1表示成累计赔付额流量三角形.用Dij代替Cij，其中根据链梯法的基本假设，各进展年间的赔付额有稳定的比例

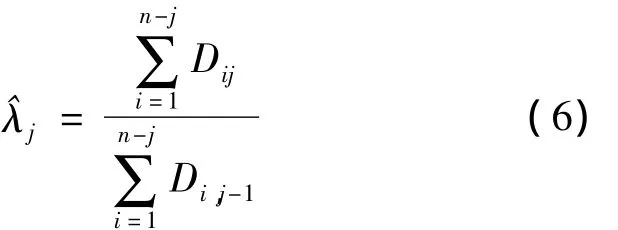
(j=1，2，…，n)称为各个发展年间的进展因子.因此，未来未决赔款准备金的预测方程为

在得到累计赔款额估计值之后，可求未来n年的赔款增量.即:

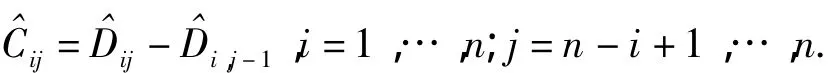
因此，可求出未来未决赔款准备金的总额V=

1.4 指数型进展因子

为了避免估计参数过多的问题出现，引进SHERMAN［3］的指数型进展因子模型:

其中，rj(j=1，2，…，n)表示各进展年的进展因子.a和b是待估参数.方程(9)等价于如下线性方程:

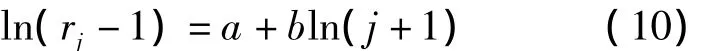
表1 流量三角形Table 1 Run－off triangle

2 区间数回归估算法及其应用

2.1 区间数回归估算法

结合流量三角形的数据特点，为充分利用数据信息，将方程(10)转换成一个区间数回归模型:

其中，Rj=ln(Min{r1j，r2j，…，rn－j，j}－1)，=ln(Max{r1j，r2j，…，rn－j，j}－ 1)，j=1，2，…，n.［a，a］和［b］是待估系数，［ε，］是一个误差项.利用NETO等［10－11］提出的区间数回归方程参数估计理论，将模型(11)转化成如下两个线性回归方程:

将上述区间数回归方法应用于未决赔款准备金评估，可分为以下4步:

(1)根据累计赔款流量三角形算出链接比三角形，如表2.

表2 链接比三角形Table 2 Link ratio triangle

(2)应用区间数回归方法计算各发展年间的进展因子.在计算出链接比三角形后，将各年的进展因子ri，j转化成区间数形式，即Rj=ln(Min{r1j，r2j，…，rn－j，j}－1)=ln(Max{r1j，r2j，…，rn－j，j}－1)，这样得到了1组区间数［Rj，］.根据区间数，［，］［，］.r=回归方法 估计出参数 和 根据j1+ea(j+1)b，计算出=1+(j+1)和=1+(j+1)，为了简化计算过程，可令区间数的期望作为进展因子的估计值

(3)确定发展因子.当j≤s时，定义表示的是发展年j到s的发展因子.

(4)预测未来累计赔偿金.根据链梯法的原则，可以得出未来累计赔偿金的计算公式:

2.2 实际应用分析

(1)赔款数据集

表3中的数据来源于某财产保险公司长尾业务的赔款数据，数据单位是万元.纵向表示的是事故发生年，横向表示的是事故发生后的进展年.各赔款数据表示的是赔款增量的流量三角形，为了方便计算，将表3转换成累积赔款流量三角形的形式(表4).

(2)估算结果

依表4数据，利用EXCEL得出链梯法的未来未决赔款准备金估算结果见表5.

表3 赔款增量数据集Table 3 Claim incremental data set

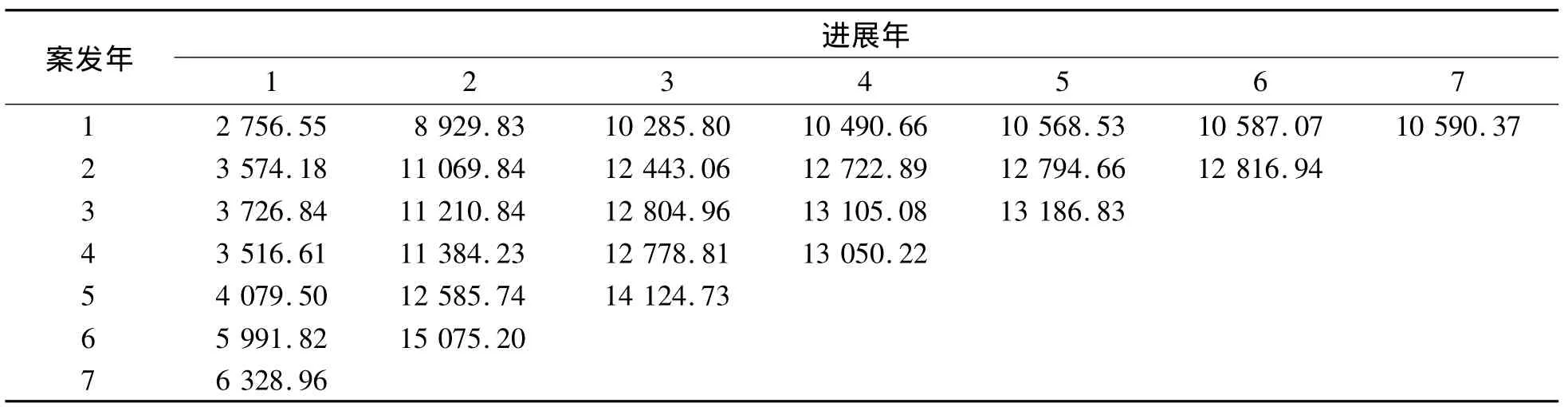
表4 累积赔款流量三角形Table 4 Cumulative claim run－off triangle

表5 链梯法结果Table 5 The results of chain ladder method

根据表4的数据，计算出链接比三角形(表6).

在表6中，令Rj=ln(Min{r1j，r2j，…，rn－j，j}－1)，=ln(Max{r1j，r2j，…，rn－j，j}－1)，得到了1组区间数据，利用区间数据回归方法，经SPSS软件估计［］，j=1，2，…，6.结果如下:

j

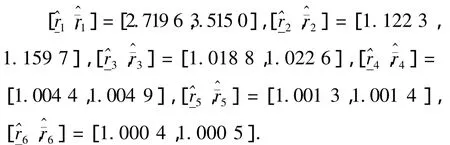
表6 实际数据中的链接比三角形Table 6 Run－off triangle in our numerical applications

为了简化计算过程，令区间数的期望E(［，，

，其作为进展因子的估计值通过EXCEL计算出未来未决赔款准备金的结果见表7.

根据表5和表7可以计算出2003年至2008年的赔款增量见表8.

由表8可见，后几年的增量赔款额逐年减少，且减少幅度越来越小，恰好符合Sherman的指数型发展模型.

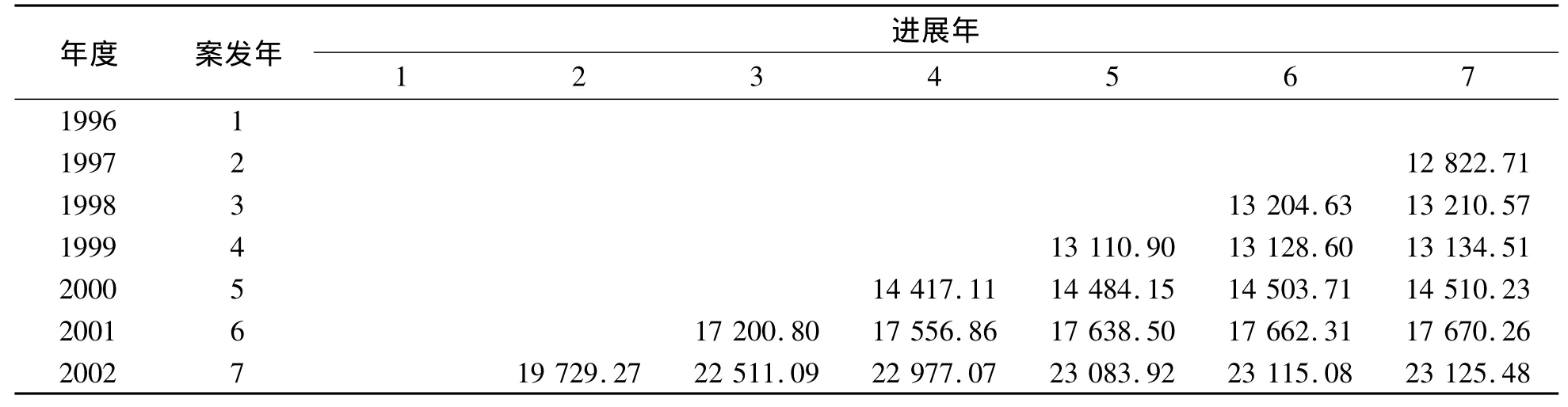
表7 区间回归模型计算结果Table 7 The results of interval regression model

表8 2003～2008年的赔款增量估计值Table 8 The estimate of claim incremental from 2003 to 2008

(3)对比分析

在计算过程中，表4中第6行第2列的数据明显与其他数据相差较大，可认为此项为异常值.为了能够比较合理地反应结果，可利用平均值去代替这个异常值.此外，在对比链梯法和区间回归方法的优劣时，本文做了如下的误差分析.用两种方法估计出来的值减去相应年份的实际赔偿额作为误差值，结果见表9.表9显示，区间数回归方法的估计值与实际值相差较小，比链梯法的估计误差明显降低.

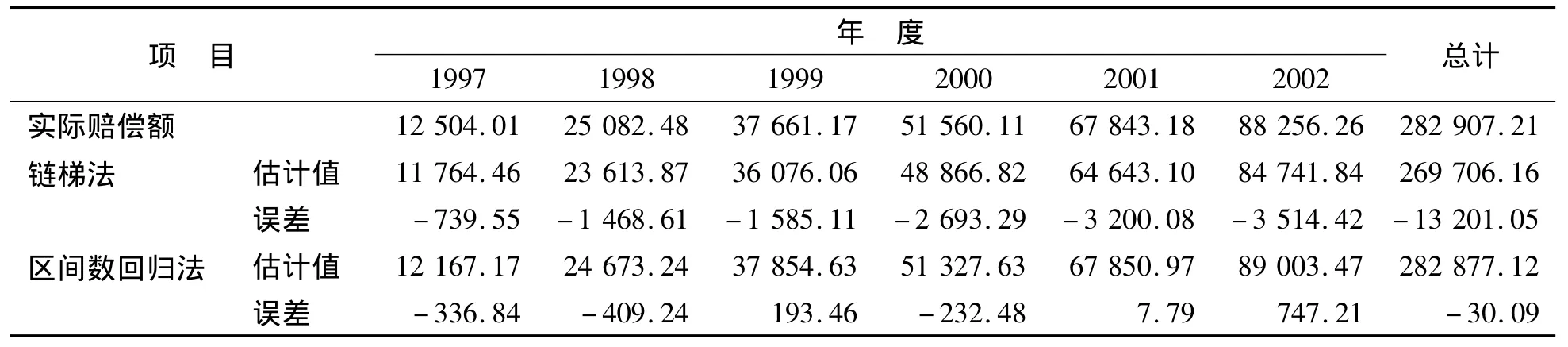
表9 链梯法与区间回归模型的结果分析Table 9 The analysis results of chain ladder method and interval regression model

3 结束语

本文尝试用区间数回归模型估算非寿险未决赔款准备金，所得结果表明区间数回归模型法相对于传统的链梯法估计效果有一定优势.链梯法易受异常值影响，估计误差通常较大.而区间数回归模型方法在缺乏分布模型的条件下，结合区间数回归的相关理论，充分挖掘和利用数据信息，从数据真实反映出险理赔规律.这种方法可较好地排除异常值的影响，且计算简便.

［1］ KREMER E.IBNR claims and the two way model of ANOVA［J］.Scand Actuar J，1982，1:47－55.

［2］ MACK T.A simple parametric model for rating automobile insurance or estimating IBNR claims reserves［J］.Astin Bull，1991，21(1):93－109.

［3］ SHERMAN R E.Extrapolating，smoothing and interpolating development factors［J］.Proc Casu Actuar Sci，1984，71:122－123.

［4］ RENSHAW A E，VERRALL R J.A stochastic model underlying the chain ladder technique［J］.Brit Actuar J，1998，4(4):903－923.

［5］ 孟生旺.非寿险准备金评估的广义线性模型［J］.统计与信息论坛，2009，24(6):3－7.MENG S W.Generalized linear models and their applications in non－life insurance loss reserving［J］.Stat Inform Forum，2009，24(6):3－7.

［6］ 卢志义，刘乐平.广义线性模型在非寿险精算中的应用及其研究进展［J］.统计与信息论坛，2007，22(4):26－31.LU Z Y，LIU L P.The applications of generalized linear models in non－life insurance and their development［J］.Stat Inform Forum，2007，22(4):26－31.

［7］ 陈迪红，陈睿.卡曼滤波在非寿险未决赔款准备金估算中的应用［J］.系统工程，2009，27(1):77－81.CHEN D H，CHEN R.Application of Kalman filter in estimating non－life outstanding claims reserving［J］.Syst Engin，2009，27(1):77－81.

［8］ SÁNCHEZ J A.Calculating insurance claim reserves with fuzzy regression［J］.Fuzzy Sets Syst，2006，157:3091－3108.

［9］ BILLARD L，DIDAY E.Regression analysis for interval－valued data［M］.Berlin:Springer－Verlag，2000:369－374.

［10］ LIMA N E A，CARVALHO F A T.Center and range method for fitting a linear regression model to symbolic interval data［J］.Comput Statist Data Anal，2008，52:1500－1515.

［11］ LIMA N E A，CARVALHO F A T.Constrained linear regression models for symbolic interval－valued variables［J］.Comput Statist Data Anal，2010，54:333－347.

［12］张博.精算学［M］.北京:北京大学出版社，2005.

ZHANG B.Actuarial science［M］.Beijing:Peking University Press，2005.

［13］张琳，王轶铭.未决赔款准备金评估模型研究［J］.江西财经大学学报，2006，45(3):41－44.ZHANG L，WANG Y M.The research of outstanding claims reserve evaluation model［J］.J Jiangxi Finan Univ，2006，45(3):41－44.