考虑桨叶陀螺效应的四旋翼定点飞行动态面控制

邵鹏杰，董文瀚，马骏，冯通

(空军工程大学 航空航天工程学院，陕西 西安710038)

0 引言

四旋翼是一个四驱动、六自由度的强耦合非线性系统，文献［1］建立了其典型的数学模型。模型中桨叶陀螺效应相比于各桨叶旋转产生的升力对机体的扭矩较小，绝大多数文献基于微小型四旋翼进行研究，为简化控制器设计，该项常被忽略［2］。随着载重的增加，对四旋翼执行机构的抗变形性提出了更高的要求;随着桨叶材质性能的提高，其转动惯量相应增大，桨叶陀螺效应对四旋翼运动的影响也随之增大。因此，建模时桨叶陀螺效应必须考虑。

实际应用中，飞行控制仍以PID方法为主。但传统PID方法有如下缺点:控制器参数较多、仅由经验选取，且提高快速性后会导致高频振荡［3］;当桨叶陀螺效应变大时，高频振荡特性将会更加凸显出来。近年来为了克服上述缺点，研究人员提出了多种非线性控制方法，比较典型的有Backstepping控制［4］、滑模控制［5］、H∞控制［6］等。文献［4］保留了对系统有用的非线性内容，设计了一种基于Backstepping方法的控制器，但其控制算法过于复杂、工程实现困难。为此，研究人员在反步法的基础上提出了动态面控制方法［7］。

本文首先针对桨叶陀螺效应对四旋翼的影响，建立了较为精准的动力学模型;然后，为了克服传统PID控制方法的缺点，提出了一种克服桨叶陀螺效应对四旋翼运动不利影响的动态面控制方法，并通过仿真试验验证了该方法的有效性。

1 四旋翼动力学建模

四旋翼结构模型如图1所示。

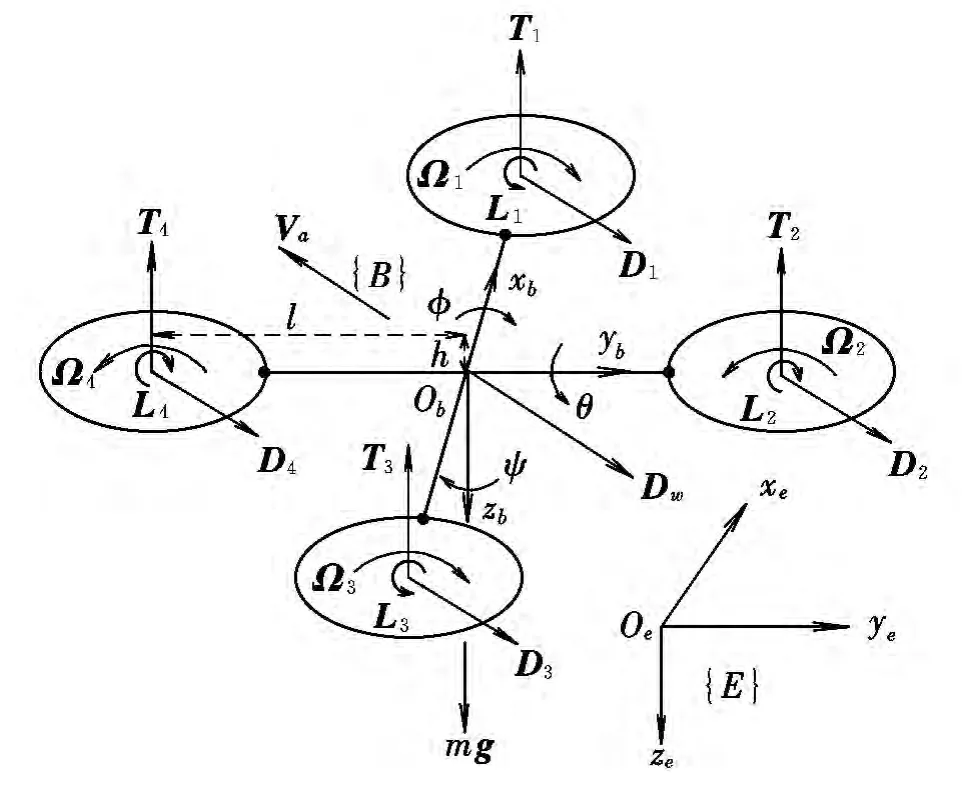
图1 四旋翼结构模型Fig.1 Structure model of quadrotor

图中:{E}系统为惯性坐标系;{B}系统为机体坐标系;l为旋翼中心到机体质心的纵向距离;h为旋翼中心到机体质心的垂直距离;Va为空速;Dw为机体与空气摩擦产生的阻力;Ωi为旋翼i的转速(i=1，2，3，4);Ti为旋翼 i产生的升力;Di为旋翼 i产生的阻力;Li为旋翼i产生的侧倾力矩;φ为滚转角;θ为俯仰角;ψ为偏航角。

四旋翼由图1中四个电机和桨叶提供动力，1，3桨叶和2，4桨叶的旋转方向相反，同时增大或减小4个电机的旋转速度可引起四旋翼的垂直运动;使1，3电机的转速反向变化，可引起四旋翼的俯仰运动;使2，4电机的转速反向变化，可引起四旋翼的滚转运动;4个电机的转速的代数和引起四旋翼的偏航运动。每个电机产生一个和电机转速Ωi的平方成正比的升力Ti，即Ti=bΩ2i［8］，b 为升力系数。

根据牛顿第二定律，系统动力学方程为:

式中:F，M分别为{E}系中加在四旋翼上的合外力、合力矩;m为四旋翼质量;V为四旋翼在{E}系中的速度;H为四旋翼在{E}系中的角动量。

现有文献中，研究对象一般为微小型四旋翼，其桨叶质量与机体质量相比较小，桨叶陀螺效应对机体运动的影响甚微，为便于研究，在建模或控制器设计过程中一般予以忽略［9］。对大型四旋翼而言，桨叶质量增大，桨叶陀螺效应随之增大，对于机体运动的影响不可忽略。因此，模型中必须引入如下桨叶陀螺效应计算公式:

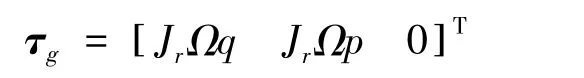
式中:Ω=Ω1－Ω2+Ω3－Ω4;q，p分别为机体绕 y，x轴的转动角速度;Ir为桨叶转动惯量。

根据受力分析可知，机体在{B}系中所受合力与合力矩为:

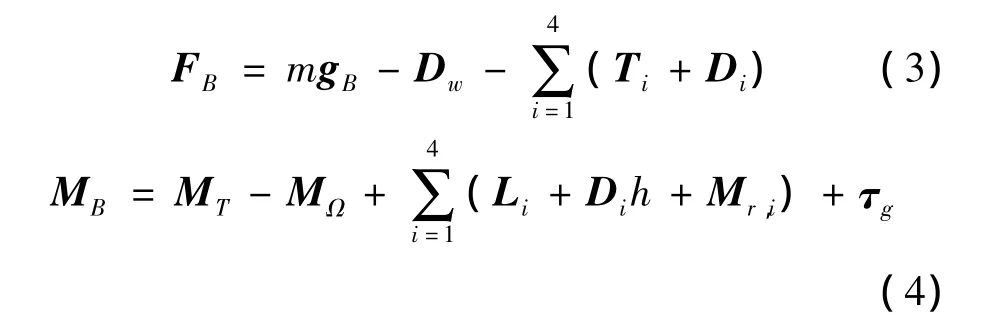
运动学方程如下:

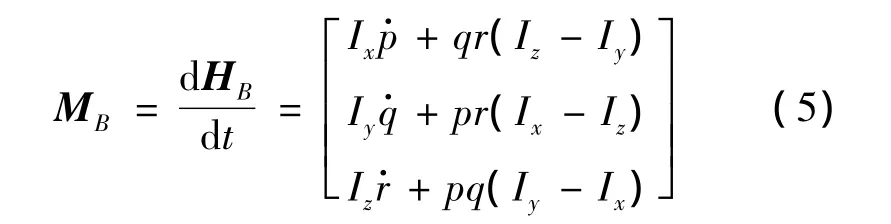
式中:Ix，Iy，Iz分别为四旋翼在{B}系中绕三轴的转动惯量。

机体坐标系到惯性坐标系的转换矩阵:

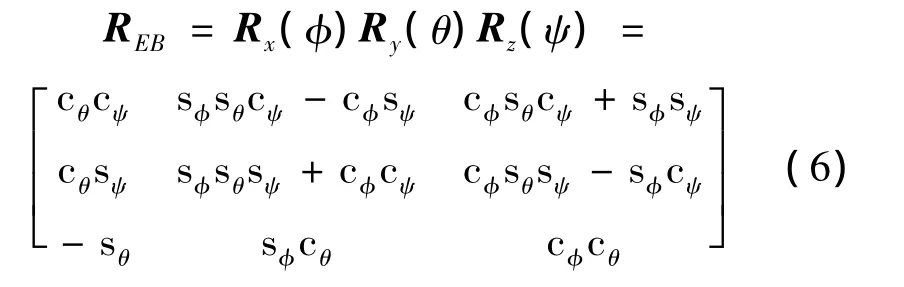
式中:c*=cos*;s*=sin*;*=θ，φ，ψ。

假设{B}系原点与质心重合，即h=0;考虑到四旋翼飞行速度慢，因此忽略小量Li，Dw，MΩ。将所有公式转换到惯性坐标系{E}中，于是得到以下考虑桨叶陀螺效应的四旋翼动力学模型:

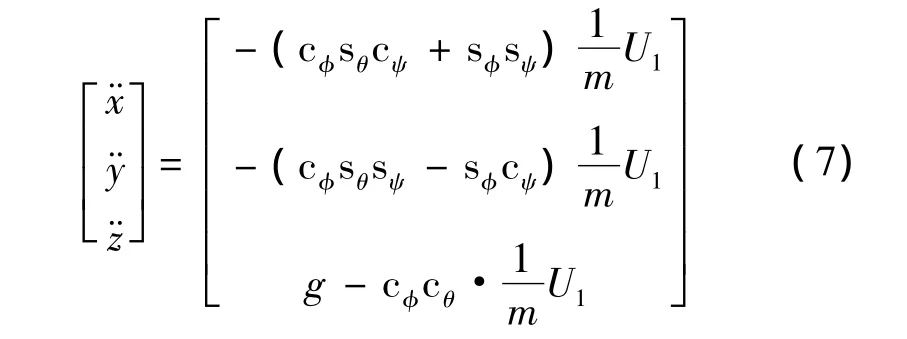
定义输入量:

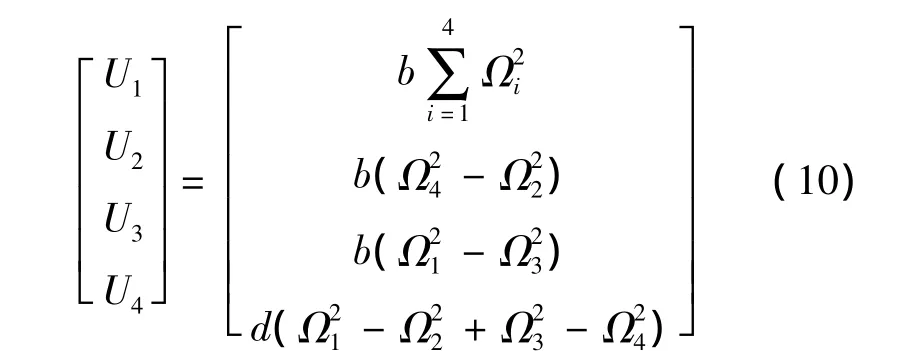
2 考虑桨叶陀螺效应的动态面控制律

2.1 四旋翼双回路控制系统

通过定义 U1，U2，U3，U4系统被分解成 4个独立的控制通道。控制器设计分为内环控制和外环控制，内环回路为姿态控制回路，外环回路为位移控制回路。四旋翼双回路控制结构如图2所示。

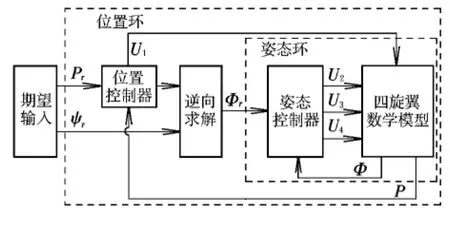
图2 控制系统结构Fig.2 Structure of control system

图中:Pr为期望位置;ψr为期望偏航角;Φr为期望欧拉角。

2.2 内环姿态控制律

考虑到桨叶陀螺效应会对机体的运动产生干扰，需要在控制器的设计中抵消桨叶陀螺效应的影响。因此，在PID-DSC控制方法［10］的基础上进行改进，对姿态环进行DSC控制设计，并分别在U2，U3通道中加入相应的抵消项本文以滚转通道控制器设计为例，进行内环姿态控制律设计。

Step1:定义动态面S1=φ－φd，对其求导得:

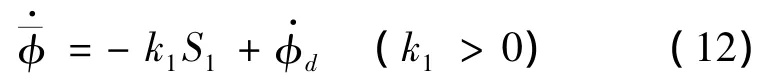
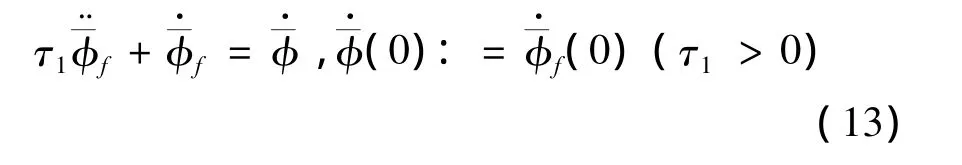
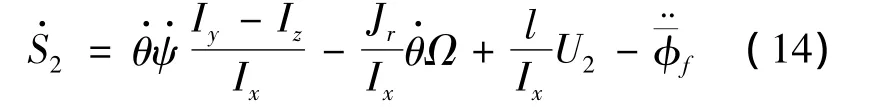
为了使S2→0，实际可取输入U2为:

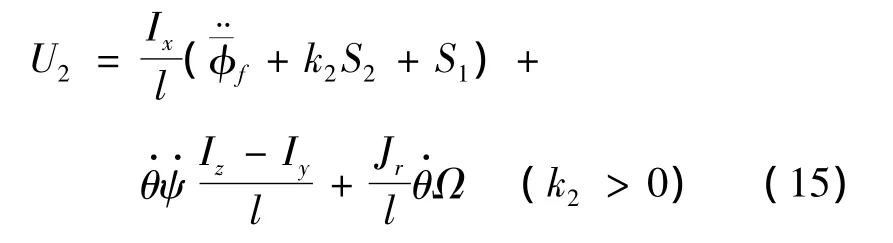
Step3:稳定性分析。定义跟踪误差为:

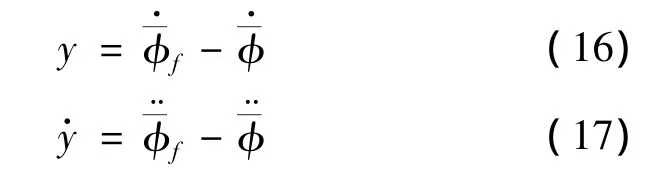
结合式(14)和式(15)，得到:

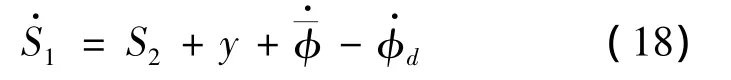
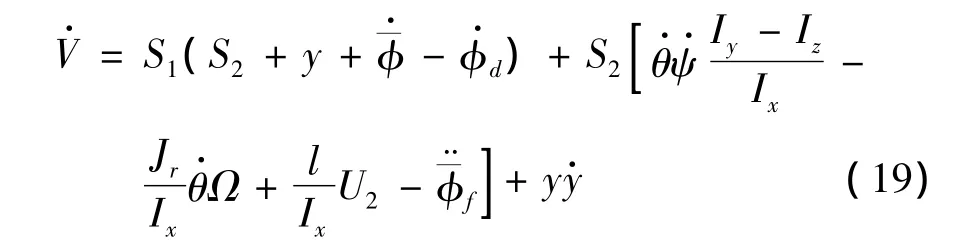
再结合式(13)和式(18)，式(19)可写为:

结合式(12)和式(14)，式(17)可写为:

很容易得到以下不等式:

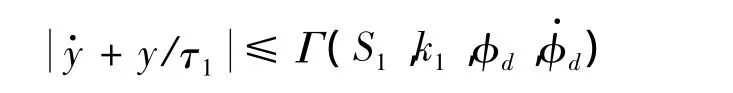
对连续函数Γ而言，若对任意的 p＞0，q＞0，满足A:={V≤p}和，则函数Γ存在一个最大值M。因此，式(20)可化为如下不等式:

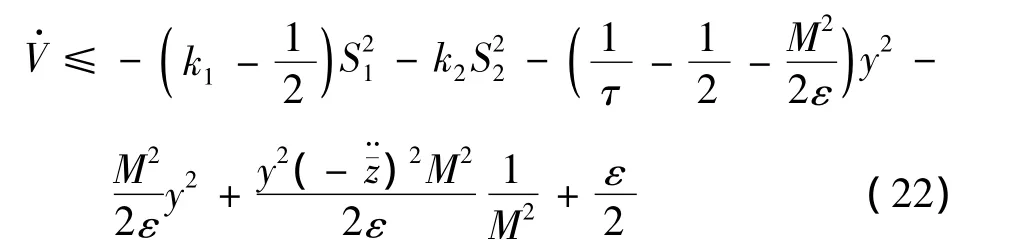
根据Lyapunov稳定性定理，上述设计过程得到的闭环系统渐进稳定。

同理，可以求得俯仰通道的控制器为:

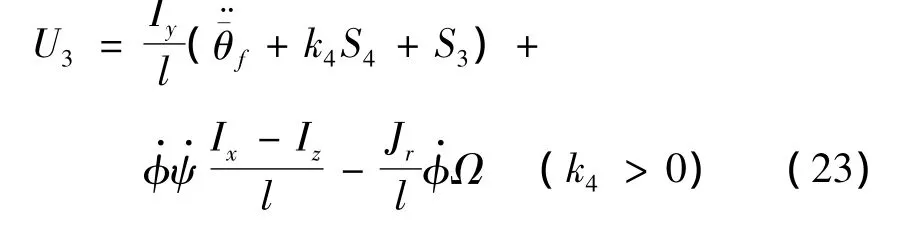
其中:

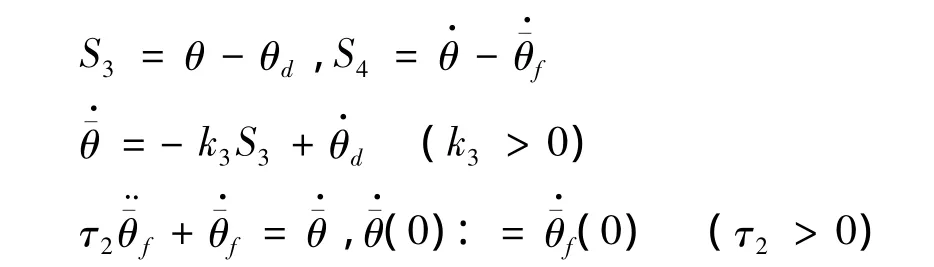
偏航通道控制器为:

其中:

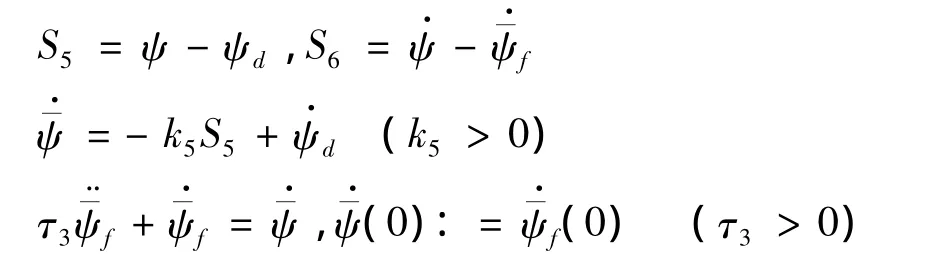
2.3 外环位置控制律

同内环姿态控制律设计，求得高度控制器为:

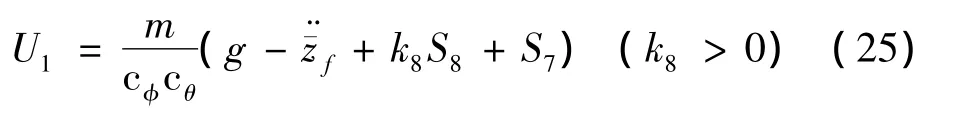
其中:

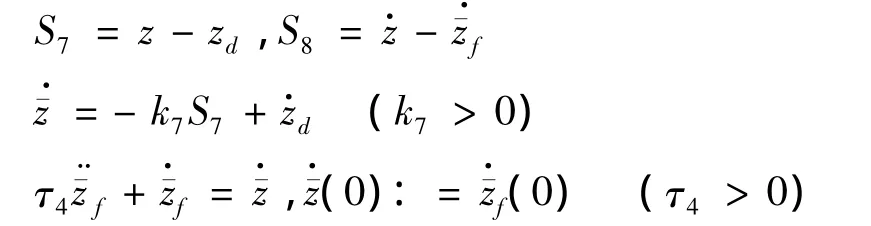
考虑到四旋翼在运动过程中姿态角变化很小(φ≈0，θ≈0)，将 U1带入式 (13)中 x方向方程可得期望滚转角φd，即:

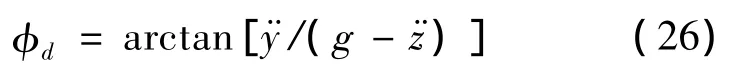
其中:

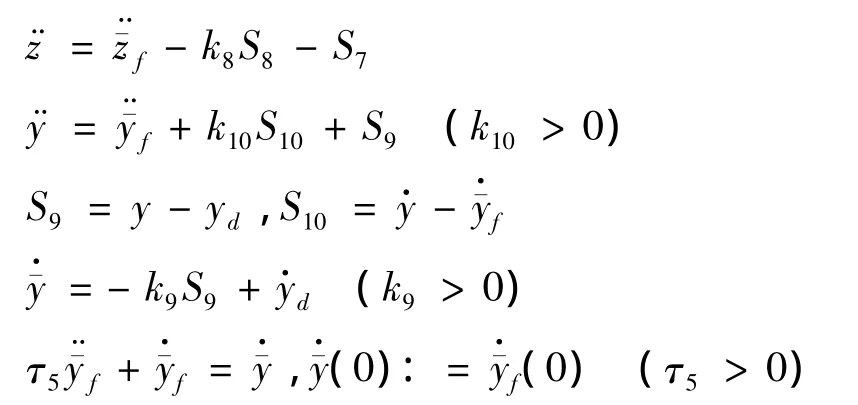
同理，将U1带入式(8)中y方向方程可得期望俯仰角 θd，即:

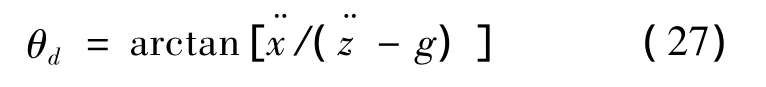
其中:

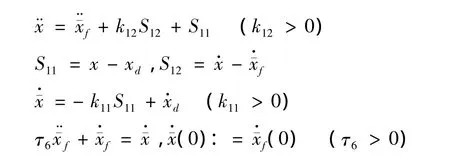
3 仿真结果及分析

为验证本文针对考虑桨叶陀螺效应所设计的DSC方法的可靠性，与文献［10］提出的PID-DSC方法进行对比试验，控制器参数分别如表1和表2所示。

表1 PID控制器参数Table 1 Parameters of PID controllers

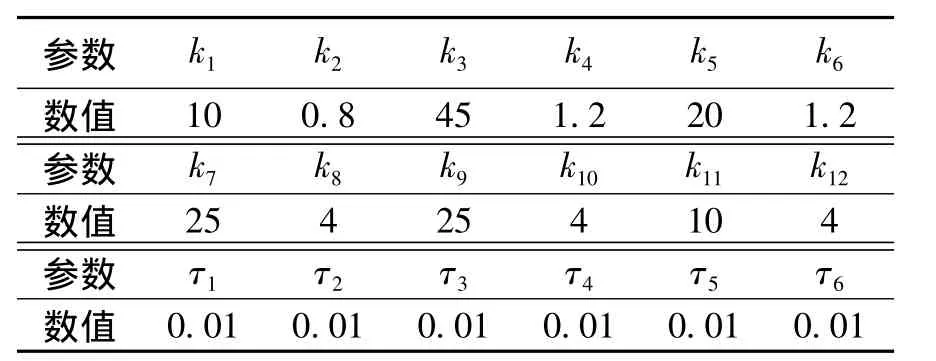
表2 DSC控制器参数Table 2 Parameters of DSC controllers

该算例令样机从惯性坐标系原点起飞，到达空间某一位置并保持悬停。设置仿真时间t=10 s。初始状态:P=(0，0，0)m，Φ =(0，0，0)rad;目标状态:P=(5，5，10)m，Φ =(0，0，0.3)rad。始末状态的线速度和角速度均为0。由于每个电机受最快转速和安全最低转速的制约，每个通道的输入均有一个阀值:U1∈［0，20］，U2∈［－5，5］，U3∈［－5，5］，U4∈［－0.182，0.182］。

本文仿真模型动力学参数为:m=1.626 5 kg，l=0.321 m，Ix=0.031 517 kg˙m2，Iy=0.031 528 kg˙m2，Iz=0.049 75 kg˙m2，Ir=0.008 kg˙m2，b=1.55e－05，d=2.82e－07。设置 3组对比仿真试验，结果如图3所示。

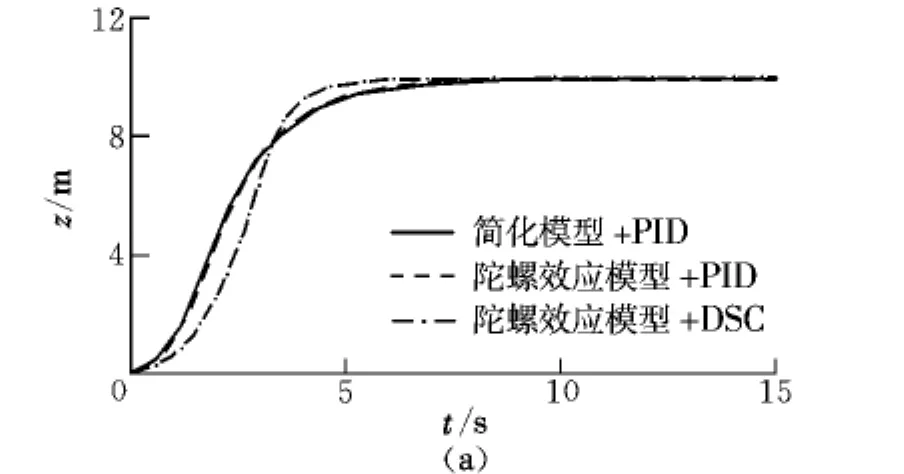
图3 位移、姿态角仿真结果Fig.3 Simulation results of position and attitude

由图3及表1、表2可以得出以下结论:

(1)不考虑桨叶陀螺效应时，PID能有效控制四旋翼，各指标调节时间ts均比较长。考虑桨叶陀螺效应时，控制器参数相同的PID控制器不能完全有效控制四旋翼，位置收敛效果较好;但姿态角收敛效果及稳定性变差，滚转角φ和俯仰角θ在平衡位置小角度高频振荡，偏航角ψ严重漂移。

(2)考虑桨叶陀螺效应时，DSC能有效控制住四旋翼，各指标收敛迅速、稳定性好，且调节时间ts均比较短。

(3)基于PID，DSC控制算法的控制器需分别设计并调试18个，12个参数，DSC算法下的控制器参数变少，简化了控制器。

4 结束语

本文提出的DSC方法能有效克服传统PID方法对考虑桨叶陀螺效应模型控制稳定性不强、部分信号漂移的缺点。该方法具有以下优点:算法比反步法简单;参数较PID控制器少，便于控制器设计;反应迅速，调节时间ts比PID控制短;稳定性强，有效克服了PID方法下出现高频振荡的缺点。

［1］ Schreier M.Modeling and adaptive control of a quadrotor［C］//Proceeding of the 2012 IEEE International Conference on Mechatronics and Automation.IEEE，2012:383-390.

［2］ Fernando H C T E，De Silva A T A，De Zoysa M D C，et al.Modelling，simulation and implementation of a quadrotor UAV［C］//2013 IEEE 8th International Conference on Industrial and Information Systems.IEEE，2013:207-212.

［3］ 李杰，齐晓慧，韩帅涛.基于GA-Vague-PID的小型四旋翼飞行器姿态控制方法［J］.自动化技术与应用，2013，32(3):1-6.

［4］ 聂博文.微小型四旋翼直升机建模及控制方法研究［D］.长沙:国防科学技术大学，2006.

［5］ Bouadi H，Simoes Cunha S，Drouin A，et al.Adaptive sliding mode control for quadrotor attitude stabilization and altitude tracking［C］//2011 IEEE 12th International Symposium on Computational Intelligence and Informatics.IEEE，2011:449-455.

［6］ 蔡国玮，陈本美，李崇兴，等.无人驾驶旋翼飞行器系统［M］.北京:清华大学出版社，2012:103-111.

［7］ Liang Yong，Li Ruitao，Zhang Youan，et al.An improved method of dynamic surface control for a class of nonlinear systems［C］//Proceeding of the 30th Chinese Control Conference.IEEE，2011:401-404.

［8］ Prouty R W.Helicopter performance，stability，and control［M］.Boston:Krieger Publishing Company，1986:20-23.

［9］ Li Sen，Li Baokui，Geng Qingbo.Adaptive sliding mode control for quadrotor helicopters［C］//Proceedings of the 33rd Chinese Control Conference.IEEE，2014:71-76.

［10］ Lee K U，Kim H S，Park J B，et al.Hovering control of a quadrotor［C］//2012 IEEE 12th International Conference on Control， Automation and Systems.IEEE，2012:162-167.