分析力学方法在弹性力学中的应用
2015-12-28张波
张波
(中煤科工集团重庆研究院,重庆 400039)
分析力学方法在弹性力学中的应用
张波
(中煤科工集团重庆研究院,重庆 400039)
摘要:分析力学中,在构建刚体的运动微分方程时,使用拉格朗日方程非常方便,因为借助拉格朗日方程来建立运动微分方程时,只需写出系统的动能和势能。现以铁木辛柯梁和小挠度矩形薄板为研究对象,沿用分析力学的方法,实现了分析力学方法在弹性力学中的应用。
关键词:分析力学;弹性力学;铁木辛柯梁;小挠度矩形薄板;挠曲线方程;最小势能原理
0引言
在经典的弹性力学书籍中[1-3],变分原理是应用最为广泛的一个原理,可是在实际模型中,对能量函数进行变分还是相对繁琐,能不能用一些方程取代这些复杂的变分过程,让应用者有公式可套,就像在分析力学一样,只要列出系统的动能和势能,借助拉格朗日方程转化,系统的运动微分方程即可确立。
与此同时,文中所提到的外力势能,摆脱了边界条件产生的外力势能,即边界条件并不参与方程的建立,它只参与方程的求解。这与弹性力学变分原理有些不同,因为在弹性力学变分原理中边界条件产生的外力势能也参与变分。在后文的工程应用中将体现这种思路,同时这种思路与分析力学也相吻合,因为在分析力学中初始条件只是在方程求解时发挥了作用,而并没有参与方程的构建。
文中建立了两个一般性的欧拉方程,并对其作出了数学证明,借助这两个方程,铁木辛柯梁和小挠度矩形薄板的挠曲线方程很快就能建立。
在方程求解方面,状态空间法[4-6]为求解弹性体的精确解析解开辟了新思路。然而状态空间法需要构建哈密顿矩阵,并求出其零本征值的本征向量和非零本征值的本征向量,这并不是件容易的事。介绍另一种能精确求解铁木辛柯梁解析解的方法,即参数法,高等数学对这种方法有过阐述,但那只是对一维问题的求解,将其引用到二维问题中来,当然实际应用时还可以将其拓展到更高维的问题中去。
1数学模型分析
第一类泛函:
K=
这个泛函取极值时应满足的条件为:
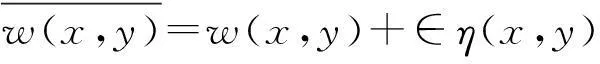
其中:∈η(x,y)在边界时函数值为零。
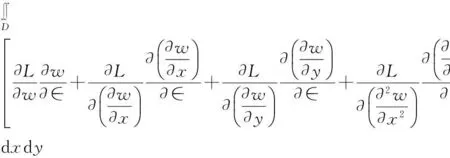

根据偏导顺序可调换有:
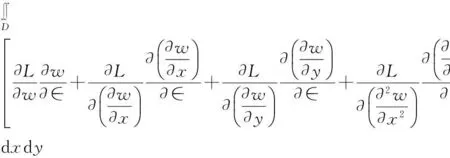

根据偏导顺序可调换有:
根据偏导顺序可调换有:
xdy=

由格林公式[7]导出:
∮(Aηdy-Bηdx)=xdy+xdy
由于边界积分为0, 故等式左边为0,那么有:
xdy=-xdy
由格林公式导出:

由于边界积分为0, 故等式左边为0,那么有:
xdy=-xdy
再由格林公式导出:

由于边界积分为0, 故等式左边为0,那么有:
-xdy=xdy
即有:
xdy=xdy
同理:
xdy=xdy
xdy=xdy
得证:
第二类泛函:

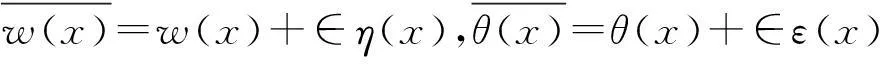
其中:∈η(x),∈ε(x)在边界时函数值为零。
根据偏导顺序可调换,有:
(1)
由于边界积分为0,那么式(1)为:
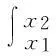

2工程应用
1) 列出在分布力q(x,y)作用下小挠度矩形薄板的挠曲线方程(x0z平面内)。q(x,y)方向向下,I为板截面绕中性轴的惯性矩,E为材料的杨氏模量,G为材料的剪切模量,μ为泊松比。
解:先将板在横截面上分成N份(单位面积)。
每份的外力势能为:T=-qw
每份的变形势能为:
V=∫vWdv=∫ΩWdΩ
其中W为板的应变比能,根据根据基尔霍夫假设[1]及应变和位移的几何关系可导出:
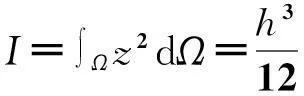

令:
故矩形薄板在外力作用下的总势能为:
根据最小势能原理δS=0及已证第一类泛函取极值的条件,得小挠度矩形薄板的挠曲线方程为:
2) 求解纵横载荷联合作用下“铁木辛柯梁”的挠曲线方程(x0z平面内)。其中横向载荷为分布力q(x)及分布外力矩M0(x),q(x)方向向下,M0(x)为顺时针,纵向载荷为拉力F。A为横截面面积,I为梁截面绕中性轴的惯性矩,E为材料的杨氏模量,G为材料的剪切模量,μ为泊松比。
解:先将长度为L的梁在长度方向上分成N份(单位长度)。
由于铁木辛柯梁需考虑剪切变形的影响,故引入两个广义位移:梁轴线的挠度w(x)及横截面转角θ(x)。
由微弧分公式有:
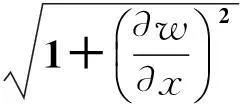
挠度作用下的轴向应变为:
每份的外力势能为:
每份的变形势能为:
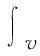
其中W为铁木辛柯梁的应变比能,根据应变和位移的几何关系有:

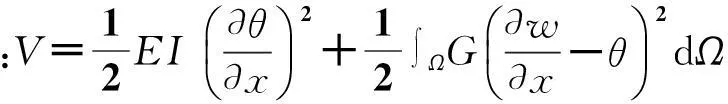
参考文献一般假定横截面上的切应力为常数,但实际并非如此,因此引入剪切修正系数k,具体可[2] ,其中k与截面有关。故:
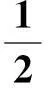
令:
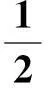
故铁木辛柯梁在外力作用下的总势能为:
根据最小势能原理δS=0及已证第二类泛函取极值的条件,得“铁木辛柯梁”的挠曲线方程为:

EI2θ+KGA=-M0(x)
将该方程组写成矩阵形式:

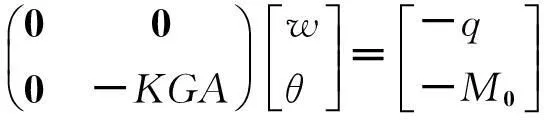
(2)
其中:
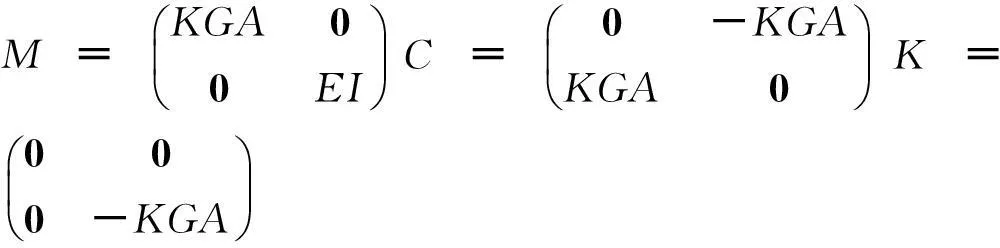

将式(2)写成矩阵形式为:
(3)
令:

那么:
(4)
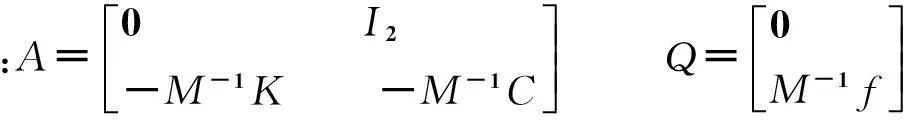
将式(4)化为积分方程[8]:
(5)
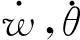
已经化简到了这一步,计算交由电脑来完成。MATLAB是一个很好的工具,在MATLAB中可以直接调用expm来处理矩阵函数eAx,int来处理积分函数,利用文献[9]的库程序可以求出S(x)的表达式。A是一个四阶矩阵,求解速度很快。
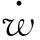
3结论
1) 文中列方程的思路几乎与分析力学中列运动学微分方程的思路一模一样,这一点在实例中得到了很好的体现。通过对铁木辛柯梁和小挠度矩形薄板的研究,实现了分析力学方法在弹性力学中的应用。
2) 已经证明的两个方程是基本方程,其桥梁作用在实例中也已经得到了很好的体现。但是这两个方程不应只局限于这两个模型,它们的作用应该得到拓展。即只要所求系统的能量函数在结构上与这两个方程类似,那么在构建方程时就可以借助这两个方程。
3) 可以看到,在构建挠曲线方程时,边界条件并没有参与方程的构建。这样的思考来源于两点:一是这一类问题都是边界已知的变分问题,即只发生弹性变形;二是由于弹性体是一个连续系统,那么在弹性体中任何一点的挠曲线方程应该是连续的,边界处也不例外。
4) 在求解铁木辛柯梁的方程时,借助参数法,实现了高阶微分方程向低阶微分方程转化的思路。当然参数法还可以应用到其他问题中去,比如多自由度系统的线性振动问题,求解其振动响应也是非常的便捷。
[1] 杨伯源,张义同. 工程弹塑性力学[M]. 北京:机械工业出版社,2003.10.
[2] 付宝连. 弹性力学中的能量原理及其应用[M]. 北京:科学出版社,2004.
[3] 姚伟岸,钟万勰. 辛弹性力学[M]. 北京:高等教育出版社,2002.4.
[4] 钟万勰. 分离变量法与哈密顿体系[J]. 计算结构力学及其应用,1991,8(3).
[5] 徐新生,邱文彪,付月,等. 辛方法在弹性圆板屈曲问题中的应用[J]. 应用力学学报,2009,9(3).
[6] 钟阳,李锐,刘月梅. 四边固支矩形弹性薄板的精确解析解[J]. 力学季刊,2009,6(2).
[7] 同济大学数学系. 高等数学第六版下册[M]. 北京:高等教育出版社,2007.6.
[8] 史荣昌,魏丰. 矩证分析[M]. 北京: 北京理工大学出版社,2005.
[9] 陈怀琛,龚杰民. 线形代数实践及MATLAB入门[M]. 北京:电子工业大学出版社,2009.1.
Application of Analytic Mechanics Method in Elasticity Theory
ZHANG Bo
(China Coal Technology Engineering Group Chongqing Research Institute, Chongqing 400039, China)
Abstract:In analytic mechanics, when differential equations of motion of rigid body are constructed, the Lagrange equation is chosen. Since the differential equation of motion is established with the aid of the Lagrange equation, it only needs writing the kinetic and potential energy of the system. This article takes the Timoshenko beams and small deflection thin plate as the research objects and the analytic mechanics method is applied to the elasticity theory.
Keywords:analytical mechanics; elastic mechanics; timoshenco beam; small deflection thin plate; equation of deflection curve; theorem of minimum potential energy
收稿日期:2014-11-29
中图分类号:TB125
文献标志码:A
文章编号:1671-5276(2015)03-0071-04
作者简介:张波(1985-),男,江西吉安人,硕士研究生,主要从事生产技术管理工作。
