连续傅里叶变换在通信原理和信号与系统课程中的应用

连续傅里叶变换在通信原理和信号与系统课程中的应用

税奇军，唐炳华，董赛鹰

(四川文理学院物理与机电工程学院，四川达州635000)

摘要：针对学生在学习通信原理和信号与系统课程中忽视连续傅里叶变换重要作用的现象，结合实例分析了连续傅里叶变换在求解连续复杂信号的频谱、复杂的广义积分和数字基带信号频谱中的作用，从而让学生在学习这两门课程的过程中熟练掌握连续傅里叶变换，为后续专业课的学习奠定坚实基础.

关键词：通信原理；信号与系统；连续傅里叶变换

收稿日期：2014-10-12

基金项目:四川省教育厅2015年度自然科学基金“光载超宽带信号传输特性研究”( 15ZB0320) ；四川文理学院2013年度教育教学改革研究项目“应用型人才培养目标下《信号与系统》和《通信原理》课程优化整合的探索研究”( 2013JY47) ；四川文理学院2013年度面上项目“基于电吸收调制器的变频技术研究”(2013Z002Z)

作者简介：税奇军( 1976—)，男，四川遂宁人.讲师, 主要从事光通信及微波光电子学研究.

中图分类号：G642.0文献标志码：A

0引言

连续信号的傅里叶变换是信号与系统和通信原理课程中非常重要的一种变化，它是将信号从时域变换到频域的方法，其反应了连续非周期信号时域特性和频域特性之间的内在联系，因此连续信号的傅里叶变换在信号与系统和通信原理课程学习中具有重要作用.[1]多年的教学实践经验表明，学生对这些知识点的掌握不够熟练，从而缺乏融会贯通的能力.文章针对这一现象通过实例分析了连续信号傅里叶变换存在的条件和连续信号傅里叶变换的应用.

1连续信号的傅里叶变换存在条件

如果一个连续非周期信号满足狄里赫利条件：(1)连续非周期信号绝对可积；(2)在任何有限区间内，连续非周期信号只有有限个最大值和最小值；(3)在任何有限区间内，连续非周期信号有有限个不连续点，并且在每个不连续点都必须有有限值.其时域和频域满足如下的傅里叶变换关系:

(1)

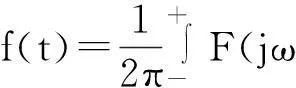
(2)

(1)式和(2)式中f(t)是连续非周期信号，F(jω)是连续非周期信号的频谱.[2]

2连续信号傅里叶变换特点

由于连续非周期信号的频谱是一个复数，所以可以将其写成模和相位的形式:

(3)

(4)

对(3)式求频谱的共轭复数后和(4)式相等，可以得到：

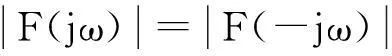
(5)

θ(-ω)=-θ(ω)

(6)

由(5)式和(6)式可以发现一连续非周期信号其幅频是偶函数，相频是奇函数.对于一个实偶连续非周期信号其频谱是实偶函数，对于一个实奇连续非周期信号其频谱是纯虚奇函数.

3连续傅里叶变换的应用

在信号与系统和通信原理课程中，连续信号傅里叶变换得到广泛应用，主要表现在分析连续确知信号频谱和随机信号频谱以及求解复杂的广义积分上.

3.1利用连续信号傅里叶变换计算复杂信号的频谱

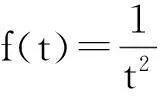
(7)

由傅里叶变换的对偶性得到：

(8)

将(8)式恒等变形可以得到：

(9)

根据傅里叶变换时域求导性质可以得到：

(10)

3.2利用连续信号傅里叶变换性质计算复杂的广义积分

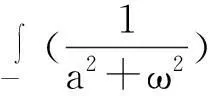
(11)

双边指数信号的频谱为：

(12)

将(12)式的时域和频域代入(11)式得到：

(13)

将(13)式恒等变形就可以立即计算出该广义积分，其结果为：

(14)

3.3利用连续信号傅里叶变换性质计算数字基带信号的频谱

数字基带信号的频谱是通信原理课程中非常重要的一个内容， 通过对数字基带信号频谱的分析可以发现信号在传输中的特性.比如信号有没有直流成分，有没有可供提取同步信号用的离散分量以及根据其连续谱可以确定基带信号的带宽.由于数字基带信号是非确知信号，所以其频谱只能用统计的方法体现功率谱密度，对数字基带信号可以将其表示成非周期的交变波和周期的稳态波，非周期的交变波的功率谱密度表达式如下：

ps(f)=fsp(1-p)

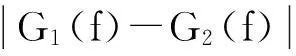
(15)

fs是二进制基带信号一个码元宽度的倒数，p是二进制码元‘0’出现的概率，G1(f)和G2(f)分别是‘0’和‘1’对应的傅里叶变换.如一个随机序列矩形脉冲表示，并且该矩形脉冲是双极性不归零，随机序列中‘0’和‘1’出现的概率相等，求其交变波的频谱.[5]根据(15)式可以得到随机序列在等概情况下交变波功率谱表达式为：

(16)

由于表示数字信号的基本码元是双极性不归零矩形脉冲，所以有：

G2(f)=-G1(f)

(17)

(18)

将(17)式和(18)式代入(16)式，可以得到该随机序列的频谱为：

(19)

4结束语

文章分析了连续信号傅里叶变换在信号与系统和通信原理课程中的重要作用，利用连续傅里叶变换能够计算和分析复杂广义积分，数字基带信号交变波的功率谱密度和复杂连续信号的频谱，为学生在学习信号与系统和通信原理课程中把握连续傅里叶变换的重要性起了一定的指导作用.

参考文献：

[1] 杨晓非，何丰.信号与系统[M].北京：科学出版社，2008:87.

[2] 刘树堂.信号与系统：第2版[M].西安：西安交通大学出版社，2000:126.

[3] 段哲明. 信号与系统[M].北京：电子工业出版社，2008:132.

[4] 陈生潭. 信号与系统[M].西安：西安电子科技大学出版社，2001:73.

[5] 樊昌信，曹丽娜.通信原理：第6版[M].北京：国防工业出版社，2008:200.

[责任编辑范藻]

The Application of Continuous Fourier Transform

in the Communication Principle and Signal & System Courses

SHUI Qijun, TANG Binghua, DONG Saiying

(Physics and Mechanical-Electrical Engineering School of Sichuan University of Arts and Sciences, Dazhou Sichuan 635000,China)

Abstract:As for the phenomenon that students tend to ignore the importance of continuous Fourier transform in learning the courses of communication principle and the signal and system, this paper, based on the case analysis of Continuous Fourier transform in solving continuous complex signal spectrum and complex generalized integral and the role of digital baseband signal spectrum, aims to improve students' mastery of continuous Fourier transform in learning these two courses and lay a solid foundation for the follow-up professional course learning.

Key words:communication principle; signal and system; continuous Fourier transform