离散序列线性卷积和循环卷积的关系
2015-12-28王益艳
离散序列线性卷积和循环卷积的关系
王益艳
(四川文理学院物理与机电工程学院,四川达州635000)
摘要:针对时域离散序列,探讨了线性卷积和循环卷积之间的关系.分析了两者等价的条件,并研究了其不等价情形下的误差范围,最后通过仿真实验证明了理论结果的正确性.
关键词:线性卷积;循环卷积;混叠误差
收稿日期:2015-08-06
基金项目:四川文理学院2013年度重点教改项目“电子学专业信号处理系列课程教学模式改革与实践”(2013JZ12)
作者简介:王益艳(1982—),男,湖北咸宁人.讲师,硕士,主要从事图像与信号处理研究.
中图分类号:O411.1文献标志码:A
0引 言
线性卷积是时域离散线性时不变(LTI)系统中最重要的运算之一,通过卷积可以有效建立系统输入和输出之间的关系.[1]另外,FIR滤波器在实际中一般都是通过线性卷积实现的.[2]而离散傅里叶变换(DFT)又是在频域实现线性系统运算的一条有效途径,通过循环卷积定理可知,[3]DFT可用来计算循环卷积.若序列x(n)的长度(即非零点的个数)为M,h(n)的长度为N,则计算两者L点(L≥max[M,N])的循环卷积yL(n)=x(n)⊗h(n)的方法如下:[4]
(1)在x(n)的尾部补L-M个零点,在h(n)的尾部补L-N个零点;
(2)分别计算L点的X(k)=DFT[x(n)]和L点的H(k)=DFT[h(n)],其中k=0,1,2,…,L-1.
(3)计算YL(k)=X(k)H(k),k=0,1,2,…,L-1.
(4)计算L点的yL(n)=IDFT[YL(k)],n=0,1,2,…,L-1.
因此,循环卷积既可以在时域直接计算,也可以在频域计算.同时,上述计算过程中的DFT和IDFT均可采用快速傅里叶FFT算法实现.[5]当L很大时,在频域计算循环卷积的速度要快得多.
与计算循环卷积一样,为了提高运算速度,人们也希望用FFT计算线性卷积.然而FFT只能直接用来计算循环卷积.因此,研究线性卷积和循环卷积的关系以及两者等价的条件具有重要的意义.[6]
1线性卷积和循环卷积等价的条件
不失一般性,假定x(n)和h(n)都是有限长序列,其长度分别为M和N.则它们的线性卷积和循环卷积可分别表示如下:[4]
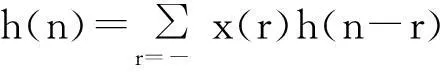

(1)
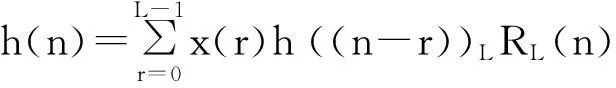
(2)

(3)
对比式(1)和式(3),可得
(4)
将式(4)代入式(3),得
(5)
式(5)表明,yL(n)等于yc(n)以L为周期的周期延拓序列的主值区间.众所周知,线性卷积yc(n)的长度为M+N-1.因此,只有当循环卷积的长度L≥M+N-1时,yc(n)以L为周期进行周期延拓时序列才没有混叠现象.此时其主值区间必定满足yL(n)=yc(n).由此证明了循环卷积和线性卷积等价的条件为L≥M+N-1.下图1给出了其Matlab实验结果.实验参数取M=8,N=5,循环卷积的点数L分别取10,12,15.
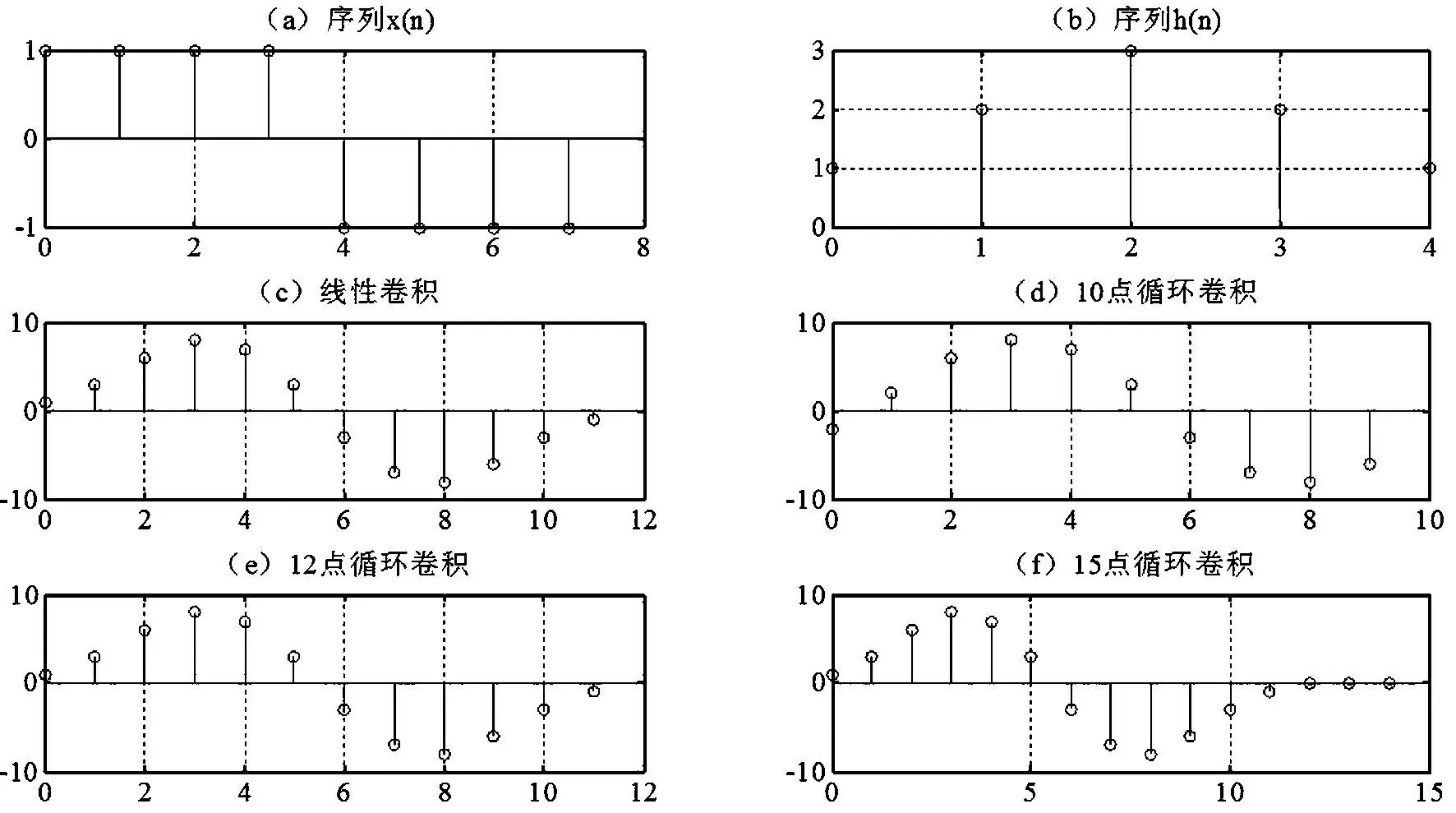
图1 线性卷积与循环卷积对比实验结果
由上述实验结果可知,线性卷积的长度为M+N-1=12(图(1-c)).因此,只有当L≥12时,循环卷积的波形才与线性卷积结果相同(即图(1-e)、图(1-f)和图(1-c)结果一样),而当L<12时,循环卷积的波形出现了一定程度的混叠失真(即图(1-d)和图(1-c)结果不一样).
2线性卷积和循环卷积不相等的误差分析
为了用DFT快速求解线性卷积,必须适当选取长度L.然而,在实际中,经常遇到两个序列的长度相差很大的情况,例如M≫N.若仍选取L≥M+N-1,以L为循环卷积的长度,并采用DFT快速计算线性卷积.则要求对较短的序列补很多零点,而且长序列必须全部输入后才能进行快速计算.这必然导致存储容量大,运算时间长,无法满足实时性的要求.而且在一些特殊的应用场合,序列长度不定或者认为是无限长,如医学超声信号和遥感信号等.[7-10]因此,在要求实时处理时,直接采用上述方法是行不通的.解决这个问题的方法一般是将长序列分段处理,具体包括重叠相加法和重叠保留法.[11]另一方面,当L取为小于M+N-1的值来做循环卷积,则必然会引起混叠,导致计算结果出现误差.下面对其误差进行分析和讨论.首先,假设L满足:
max(M,N)L (6) 根据式(5),令误差e(n)为 (7) 因为L≥max(M,N),仅有对应于m=±1的两项保留在式(7)的求和运算中,所以 e(n)=[yc(n+L)+ yc(n-L)]RL(n) (8) 一般来说,x(n)和h(n)都是因果序列,因此两者的线性卷积yc(n)也是因果的,则 yc(n-L)=0;0nL-1 (9) 所以, e(n)=yc(n+L);0nL-1 (10) 式(10)表明,当max(M,N)L 图2 线性卷积与循环卷积混叠误差实验结果 测试指标长度有效范围序列x(n)M=200,1,2….19序列h(n)N=90,1,2,….8线性卷积M+N-1=280,1,2,….2720点循环卷积误差Δ1=(M+N-1)-L1=28-20=80,1,2,….720点循环卷积正确值L1-Δ1=20-8=128,9,10,….1924点循环卷积误差Δ2=(M+N-1)-L2=28-24=40,1,2,324点循环卷积正确值L2-Δ2=24-4=204,5,….2326点循环卷积误差Δ3=(M+N-1)-L3=28-26=20,126点循环卷积正确值L3-Δ3=26-2=242,3,4,….25 由上述实验结果可知,当max(M,N)L 3结语 本文从理论分析的角度研究了离散序列两种卷积的关系,发现循环卷积本质上可以看成线性卷积以其长度为周期的周期延拓序列的主值序列,从而得出两者相等应满足的条件.同时还对两者不相等情形下的误差进行了探讨,得出了相应误差点的个数和范围.最后,通过Matlab仿真实验,验证了该结论的正确性. 参考文献: [1] Won Y. Yang.SignalsandSystemswithMATLAB:影印版[M]. 北京: 电子工业出版社, 2012:13-20. [2] Philips L, Parr M, Riskin E A.Signals,Systems,ansTransforms[M]. Fourth Edition, NJ, Pearson Education Inc, 2008: 213-227. [3] Vinary K. Ingle.DigitalsignalprocessingusingMatlab:影印版[M]. 北京: 科学出版社, 2003:125-131. [4] 程佩青. 数字信号处理教程[M]. 北京: 清华大学出版社, 2007:103-110. [5] Vinay K. Ingle, John G. Proakis.数字信号处理:MATLAB版[M].刘树棠,译. 西安:西安交通大学出版社, 2008:134-140. [6] 伍世云, 王益艳. Matlab在DSP课程教学中的几个典型应用[J]. 计算机与现代化, 2011(8):185-189. [7] 宋寿鹏, 李萍萍. 基于卷积模型的超声回波分离技术及其应用[J]. 仪器仪表学报, 2009(6):1175-1179. [8] 朱莉莉, 李晖, 谢树森. 用去卷积法提高超声调制光学成像的空间分辨率[J]. 激光生物学报, 2008(1): 110-114. [9] 许姜严, 王卫星. 基于平均加权四元数卷积的岩石节理裂隙检测[J]. 光电工程, 2009(10): 76-80. [10]陈奋, 赵忠明. 遥感影像反卷积复原处理[J]. 数据采集与处理, 2008(2): 168-175. [11]高西全, 丁玉美. 数字信号处理教程:第三版[M]. 西安: 西安电子科技大学出版社, 2008:90-93. [责任编辑范藻] Relationship Between Linear Convolution and Circular Convolution of Discrete Sequence WANG Yiyan (Physics and Mechanical-Electrical Engineering School of Sichuan University of Arts and Sciences, Dazhou Sichuan 635000,China) Abstract:The relationship between linear convolution and circular convolution is discussed for time-domain discrete sequence in this paper. It not only analyzes the equivalent condition of two convolutions, but also studies the range of error under in-equivalent situations. Finally, the theoretical results are proved by simulation. Key words:linear convolution; circular convolution; aliasing errors