大动脉血管中孤立子波的性质分析*

*基金项目:山东省自然科学基金(项目编号:ZR2012AM021)。

大动脉血管中孤立子波的性质分析*

*基金项目:山东省自然科学基金(项目编号:ZR2012AM021)。

岳超刘照军张敬军张东升李海霞孙艳丽卢海威张兆臣

(泰山医学院，山东 泰安271000)

摘要：目的分析大动脉血管中孤立子波的性质及意义。 方法运用齐次平衡法求血管壁应变满足的Kdv方程的解。 结果验证了大动脉血管中存在孤立子波。 结论从临床应用的角度看, 可以通过检测血管壁应力孤立子波的参数来辅助诊断大动脉血管病变。

关键词：应力孤立字波； 约化摄动分析；色散关系； 齐次平衡法

Analysis on characteristic of solitary waves in large arterial vessel

YUEChaoLIUZhao-junZHANGJing-junZHANGDong-shengLIHai-xiaSUNYan-liLUHaiweiZHANGZhao-chen

(Taishan Medical College, Taian 271000 , China)

Abstract:Objective:To analyse the characteristic and significance of solitary waves in large arterial vessel. Methods: Using the homogeneous balance method to obtain solution of KdV equation strain satisfied for vessel wall. Results: Verified the existence of solitary waves in large arterial vessel. Conclusion: From the point of view of clinic application, we can diagnose large arterial vessel diseases assistantly by testing the parameters of the vessel wall stress waves.

Key words:stress solitary waves；reductive perturbation analysis； dispersion relation；the homogeneous balance method

从20世纪60年代以来, 许多学者关于血液流动做了大量的研究工作[1-4]。 具体到大动脉血管中血液流动的研究，要考虑大动脉中通常同时存在着血液流动与血管壁运动的耦合。 据文献[5]的结论可知, 由于血液流体体积模量(K) 远大于血管壁材料杨氏模量(E) , 所以人体血液内的扰动一般以血管壁应力波的形式传播。在文献[6]中，作者进一步分析了血管壁应变满足的波动方程及其孤立子波解的意义。本文运用齐次平衡法求出了血管壁应变满足的KdV方程的解，并以髂动脉为例, 将正常人的生理参数代入大动脉血管壁应变表达式，借助于计算机作图，验证了大动脉血管壁扰动正是以应力孤立子波的形式传播的结论。从临床应用的角度看, 可以通过检测血管壁应力孤立子波的参数来辅助诊断大动脉血管病变。

1对象与方法

1.1研究对象大动脉血管壁应力孤立子波的存在与性质，以髂动脉为例。

1.2方法

1.2.1建立大动脉血管壁应变演化的波动方程

我们所研究的大动脉血管, 在理论上一般都认为是充满血液流体的、无限长且各向同性的直圆弹性管。根据文献[4], 给出大动脉中血液流动时满足的连续性方程和运动方程

其中μ(x,t)是血液流动的速度，A(x,t)为大动脉血管的横截面积，ρ0是血液的密度，p(x,t)表示血液流动时血管壁内外的压强差。 假设在内部压力作用下， 动脉血管半径由平衡时的r0变为r，在轴对称坐标下各个应变分量[7]如下

两个应力分量分别为

其中E为血管壁的杨氏模量。 在弱非线性条件下，由(3) 式可得

r=r0(1+εr)，A(x,t)=πr2(x,t)

=A0(1+εr)2≈A0(1+2εr)(5)

于是, 方程(1) 可变形为

由(4)式可得用血管壁应变表示的血管壁运动控制方程

其中ρw和h分别是血管壁的密度和厚度。引入无量纲变换

将(8) 式代入方程(2) , (6) , (7)可得

1.2.2色散关系分析

为了研究大动脉血管壁应力波的特性, 可采用摄动方法对方程(9) , (10) , (11) 作如下色散分析，首先设

将(12) 式分别代入方程(9) , (10) , (11) , 计算得到如下线性方程

1.2.3非线性方程的约化摄动分析

引入如下变换[8]

将其代入方程(9)，(10)(11)并作摄动展开

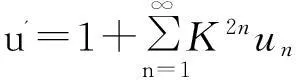
进一步计算可导出KdV方程：

下面运用齐次平衡法[9-16]求其解。设其解为如下形式：

ε1=f' 'zξ2+f'zξξ(16)

其中f=f(z),z=z(ξ,ν)为待定函数。

将(16)式代入(15)式并整理， 可得：

令6f''f'''+f(5)=0(18)

解之得f=2lnz。进而可得如下关系，

f＇f＇ ＇=-f＇ ＇ ＇，f＇ 2=-2f＇ ＇(19)

利用(18)和(19)式，(17)式可简化为：

令f＇ ＇ ＇，f＇ ＇,f＇的系数为零，只须z(ζ,v)满足

zζv+zζζζζ=0(20)

由于齐次方程有指数形式的解，依齐次平衡法设z(ζ,v)=1+ec1ζ+c2v，代入(16)，(20)，(21)得

2结果与讨论

为了研究大动脉血管壁应力孤立子波的实际意义， 我们将(22) 式代入(14) 式，得到无量纲的应变表达式， 再把结果代回(8)式, 得到含有实际参数的大动脉血管壁应变表达式

图1

图2

我们以髂动脉为例, 将正常人的生理参数[17]代入(23) 式。 这里髂动脉血管壁的杨氏模量取E=7×105N·m-2，血管壁厚度h=0.002m，血管受平衡压强时的半径r0=0.013m，血液的密度ρ0=1050kg·m-3，血管壁的平均密度ρw=1060kg·m-3。在这里考虑长波近似, 波数k=0.3。图1中表示了在这种情况下髂动脉血管壁应力波随时间t和位置x变化的图像, 从前到后分别为时间间隔0.02s的应力孤立子波波形。根据图1 所计算的应力波的波速约为7.1611m·s-1，与实验结果(6.78～7.17m·s-1)吻合，从而进一步验证了大动脉血管壁扰动正是以应力孤立子波的形式传播的结论。从(23) 式还可以看出, 当人体内血管发生病变时, 其杨氏模量、厚度将随之变化, 血管壁应力波的波速、振幅都会相应改变。图形会给我们更为直观的效果。例如再取E=5.5×105N·m-2，h=0.0023，其余参数不变，可得图2，此时波速约为6.8071m·s-1，振幅减小，所以, 从临床应用的角度看, 可以通过检测血管壁应力孤立子波的参数来辅助诊断大动脉血管病变。

参考文献:

[1]WomersleyJR.Oscillatoryflowinarteries:Theconstrainedelastictubeasamethodofarterialflowandpulsetransmission[J].PhysicsofMedicineandBiology, 1957 , 2 : 178 -187.

[2]柳兆荣, 李惜惜. 关于脉图的分析[J]. 中国科学(B辑) , 1983 , 34 (2) : 131-138.

[3]袁凡, 吴望一. 脉象的血管位移波理论[J]. 应用数学与力学, 1989 , 10 (6) : 238-242.

[4]YomosaS.Solitarywavesinlargebloodvessels[J].JournalofthePhysicalSocietyofJapan, 1987 ,56 (2) : 506-520.

[5]陶祖莱. 生物流体力学[M]. 北京: 科学出版社, 1984.

[6]易金桥. 人体动脉血管中非线性波的特性研究[M],西北师范大学硕士学位论文.

[7]陈金娥. 动脉中脉搏波的分析与数值计算[J]. 上海力学, 1982 , 3 (2) : 79-81.

[8]刘式适, 刘式达. 物理学中的非线性方程[M]. 北京: 北京大学出版社, 2000.

[9]WangMingliang,ExactsolutionsforacompoundKdV-Burgersequation[J].Phys.Lett.A. 1996,213(5-6):279-287.

[10]FanEngui,Twonewapplicationsofthehomogeneousbalancemethod[J].Phys.Lett.A.2000,265(5-6):353-357.

[11]范恩贵,张鸿庆.非线性波动方程的孤波解[J].物理学报, 1997,46(7):1254-1258.

[12]Zhang,Yufeng，HonY.C.，MeiJianqin，Asystematicmethodforsolvingdifferential-differenceequations[J].Commun.NonlinearSci.Numer.Simul.2010,15(10):2791-2797.

[13]张玉峰，张鸿庆.Burgers-KdV方程的二类行波解[J]. 应用数学和力学, 2000,21(10),1009-1012.

[14]夏铁成, 张鸿庆, 闫振亚. 一类非线性演化方程新的显式行波解[J]. 应用数学和力学, 2001, 22(07),701-705.

[15]XiaTiecheng，XiongShouquan.Exactsolutionsof(2+1)-dimensionalBogoyavlenskii'sbreakingsolitonequationwithsymboliccomputation[J].Comput.Math.Appl. 2010,60(3):?919-923.

[16]ZhangSheng，XiaTiecheng.Variable-coefficientJacobiellipticfunctionexpansionmethodfor(2+1)-dimensionalNizhnik-Novikov-Vesselovequations[J].Appl.Math.Comput.2011,218(4): 1308-1316.

[17]RF施密特,G特夫斯. 人体生理学[M]. 北京: 科学出版社,1991:1-80.

收稿日期(2014-11-20)

doi:10.3969/j.issn.1004-7115.2015.02.001

中图分类号：O29

文献标识码：A

文章编号：7115-1004(2015)02-0121-03

通讯作者：张兆臣，E-mail:zczhang@tsmc.edu.cn。

作者简介:岳超(1971—)，男， 山东泰安人，副教授， 主要研究方向: 孤立子方程求解与可积系统。