中频逆变器数字控制延时的线性化近似

刘春喜，陈鹏荣，高 姬，杨玉岗

（辽宁工程技术大学电气与控制工程学院，葫芦岛125105）

引言

逆变电源采用数字控制的特有问题之一是由采样、计算及数字PWM等过程产生的延时会对系统的动态和稳态特性产生较大影响，由于延时的存在，系统带宽被减小，在某些情况下，系统会发生振荡甚至失去稳定性[1-2]。在中频400 Hz系统中，基波频率是50 Hz的8倍，因此相同的延时会有更大的影响[3-4]。 文献[5-7]采用数字控制方法来改进 400 Hz系统的控制性能，但并未考虑数字延时带来的影响；文献[3-4,8]考虑了数字延时带来的影响，并通过控制方法来消除延时的影响，不可避免会增加系统的复杂性；文献[9]详细分析了数字控制延时对工频系统性能的影响，但没有分析延时对中频系统的影响；文献[10]分析了各种SPWM方法产生的数字控制延时，但并没有在考虑延时的情况下对系统控制参数进行设计。

解决中频逆变器数字控制延时问题的最简单方法是在系统控制器设计时考虑延时的影响，保证控制系统具有合适的相角裕度。而延时环节本身是一个非线性环节，在采用传统的频域方法设计系统时，需要对其进行线性化近似。本文分析了延时环节对400 Hz系统频域特性的影响，并对延时环节不同阶数的Pade近似进行了比较，给出了适合于中频400 Hz逆变器的Pade近似方法。最后通过一个400 Hz逆变系统的设计和实验对理论分析进行了验证，实验结果验证了理论分析的正确性。

1 逆变器等效延时环节

单相H桥逆变器的数字控制结构如图1所示。图中，Ed为直流侧电压，L、C分别为输出滤波电感和电容，r为滤波电感等效串联电阻、死区效应等各种阻尼因素的综合等效电阻。反馈变量v被检测后，经信号调理、A/D采样，变成数字量输入至处理器中，与参考信号比较后，按照所设计的控制规律，求得控制量的调制信号m，并输出到数字PWM模块，与载波进行比较，得到控制脉冲信号，这些信号经驱动电路放大后去控制开关管。

图1 逆变器数字控制结构Fig.1 Topology of inverter digital control

逆变电源的数字控制可采用不同采样方法[10]。以单极性不对称规则采样法为例，如图2所示，分析数字控制延时对系统性能的影响。图2（a）为调制波 m（k）的采样数据，k，k+1，k+2，……为采样时刻点；图 2（b）为载波 c（t）与调制波 m（k）的比较图，载波c（t）数据变化较快，可近似认为是连续变化；图 2（c）为输出电压 uo（t）波形。 采样周期 Tsm等于载波周期Tcr的1/2，在载波过零点和峰值点时开始采样，并更新调制波数据为上一个采样周期计算所得到的值，脉宽数据更新时刻相对于采样时刻滞后Tsm。数字SPWM过程可近似为一个延时环节，延时时间为Tsm/2。采用不对称规则采样，从开始采样到输出相应的脉冲宽度，总延时为3/2 Tsm，其中采样计算引入的延时为Tsm，零阶保持引入的延时为Tsm/2。单极性调制时，开关器件的开关频率fs为采样频率 fsm的 1/2。

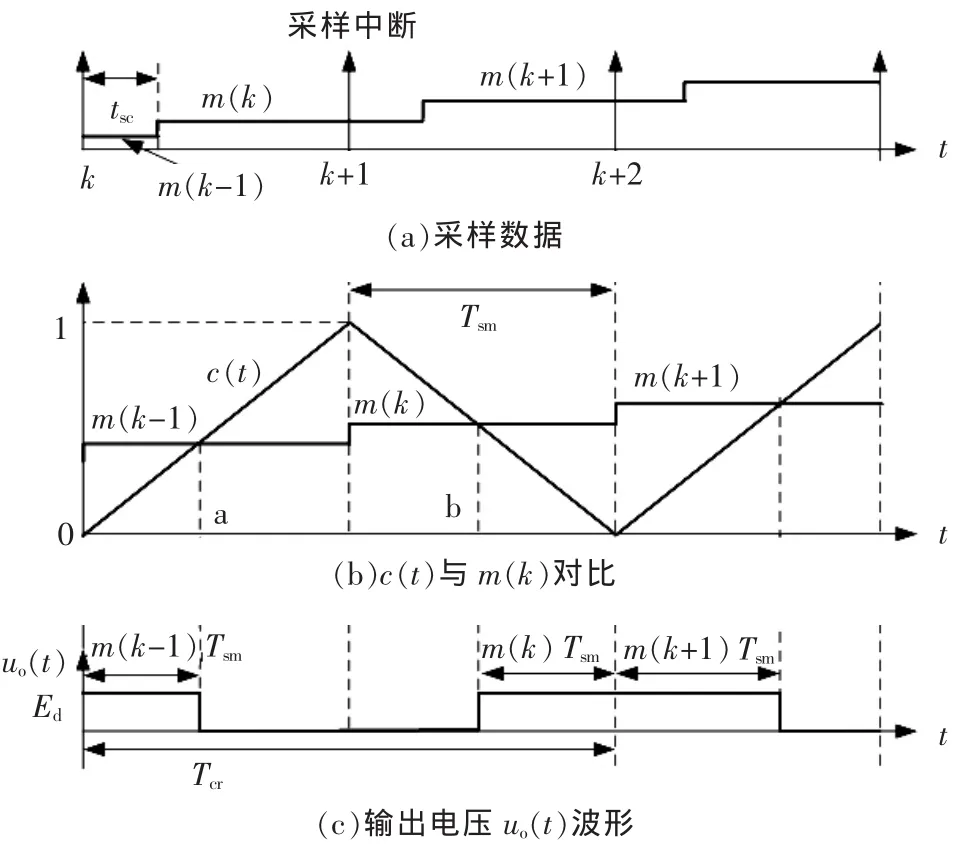
图2 不对称规则采样PWMFig.2 Asymmetric uniformly sampling PWM

采用上述PWM方法，不同开关频率或采样频率时的数字控制延时如表1所示。

表1 不同采样频率时的数字控制延时Tab.1 Digital control delay with different switching frequencies

2 延时对逆变器系统频域特性的影响

2.1 延时环节的频率特性

如果线性系统G1（s）中引入时间滞后，那么它的传递函数 G（s）会包括一个 e-τs项（τ为延时时间，τ＞0），即

函数e-τs在整个复平面是解析的，没有有限的极点和零点。延时项的频域响应由它在虚轴上的幅值和相位来确定。对所有的频率f，延时环节的幅值和相位分别为

由式（2）、式（3）可知，延时只影响系统相频特性，不影响幅频特性。对于f＞0，它的相位是负的，且呈线性递减。

若H桥逆变器的开关频率fs为40 kHz，则采用不对称规则采样PWM方法数字控制延时时间τ为37.5 μs（见表1）。则延时环节的频域特性如图3所示，图中相位单位为（°），而式（3）中得到的相位为rad。

图3 τ=37.5 μs时延时环节的频域特性Fig.3 Frequency domain characteristic of the delay when τ is 37.5 μs

由图3可见，延时引起的相位滞后和频率成线性关系。 在 50 Hz处为 0.675°，400 Hz处为 5.4°，500 Hz处为 6.75°，在 4 000 Hz处为 54°。 对于工频系统，该延时在其带宽频率（一般为基波频率的10倍左右）附近引入的相位滞后约为6.75°。这时，按传统的控制系统设计方法，留30°～60°的相位裕量，仍能得到合适的控制参数。对于400 Hz系统，该延时在其带宽频率（若仍取基波频率的10倍左右）附近引入的相位滞后约为54°。这时，控制系统设计时再留30°～60°的相位裕量，得到的控制系统将会不稳定，或稳定性很差。所以基波频率较高时，延时引起的相位滞后较大，不利于系统带宽的提高。若不考虑延时，仍采用传统的控制要求来设计基波频率较高的系统，会使系统稳定性很差甚至不稳定。

若开关频率fs为8 kHz，则延时时间τ为187.5 μs，延时环节的频域特性如图4所示。延时引入的相位滞后在50 Hz处为3.37°，在 500 Hz处为33.7°。开关频率越低，同样的延时在系统带宽频率处引入的相位滞后越大。因此，在设计工频系统时，若开关频率较低，也必须考虑延时的影响。

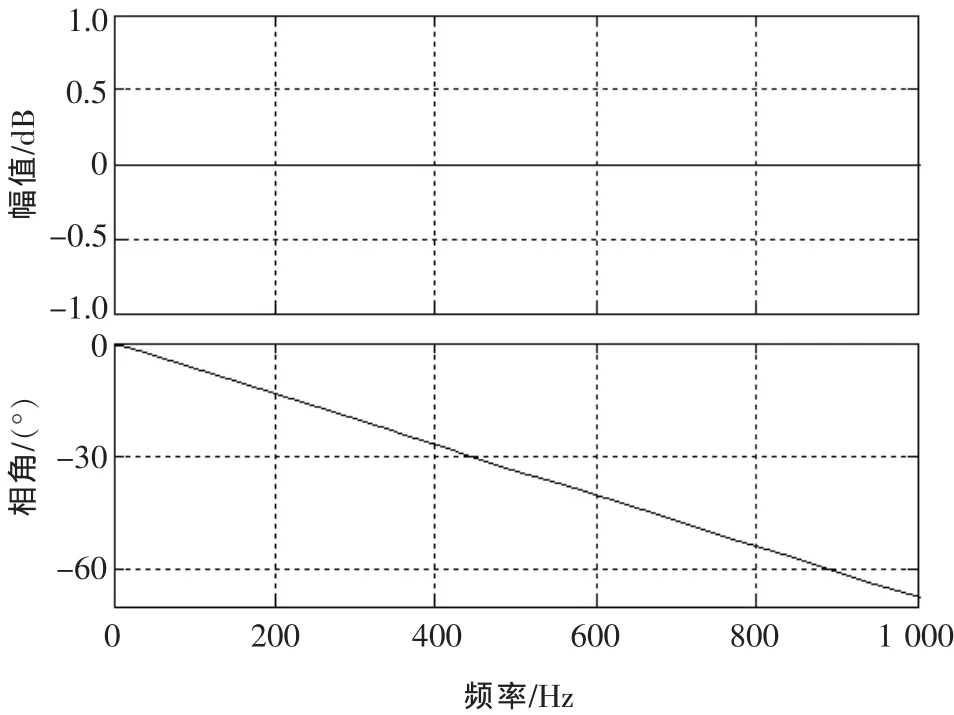
图4 τ=187.5 μs时延时环节的频域特性Fig.4 Frequency domain characteristic of the delay when τ is 187.5 μs

2.2 Pade近似分析

e-τs是一个无理函数，若在系统中直接加延时环节e-τs，分析会比较困难。通常需要用有理函数来近似代替延时环节e-τs，以简化设计过程。近似的方法有多种，例如Pade近似、Bessel函数和拉格朗日多项式等[11]。在这些方法中，Pade近似更为精确，其表达式为

l、k的值越大，近似就越精确。表2给出了1～4阶的Pade近似表达式。

表2 Pade近似表达式（l=k）Tab.2 Pade approximation

当数字控制引入的延时时间τ为187.5 μs时，1～4阶Pade近似的阶跃响应曲线和相频特性如图5所示。由图5（a）可知，阶数越高，近似就越精确，但计算量越大，所以应综合选取Pade近似的阶数。

图5 Pade近似的阶跃响应和相频特性Fig.5 Step response and phase-frequency characteristic of Pade approximation

延时环节主要影响系统的相频特性，使系统在同一频率处的相位滞后增大，而相位滞后的增大必然使系统稳定性变差。400 Hz逆变系统基波频率较高，为了得到好的系统性能，必然要求系统具有较大的带宽，这样，延时对400 Hz逆变系统的影响更大。当延时时间τ为187.5 μs时，1～4阶Pade近似的相频特性曲线如5（b）所示。由图可见，频率越高，Pade近似与实际延时的相频特性差别越大。1、2阶Pade近似与实际延时特性的相位滞后较大，当f＜3 000 Hz时，3阶近似与实际延时特性基本重合。因此，对于这种情况下，使用3阶Pade近似即可。

3 考虑延时的比例谐振控制系统设计

单相逆变器主电路参数为：输入电压Ed=50 V，开关频率fs=5.6 kHz，采样频率fsm=11.2 kHz，基波频率 fo=400 Hz，滤波电容 C=40 μF，滤波电感L=136 μH，阻尼电阻 r=0.35 Ω，输出电压 Uo=11 V。

考虑延时环节的逆变器控制框图如图6所示。图中，Gv（s）为控制器函数（其中包含逆变桥增益），Gd（s）为延时等效环节。若把负载电流看作一个干扰输入，则控制系统的开环传递函数Uo（s）为

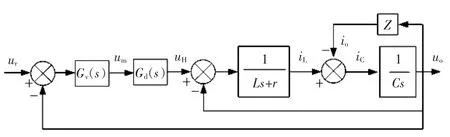
图6 逆变器控制框图Fig.6 Control block diagram of inverter

控制器采用比例谐振控制[12]，则 Gv（s）的表达式为

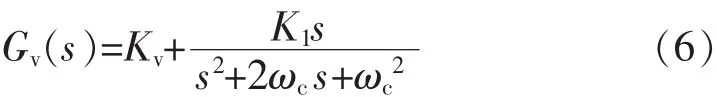
式中：Kv为比例系数；K1为基波谐振系数；ωc为谐振控制器的截止角频率；ω为基波角频率。采用不对称规则采样时，数字控制延时为3/4 Ts，可采用3阶Pade近似来进行系统参数设计。根据参数根轨迹法[13]，可得 Kv＝0.2，ωc＝10 rad/s，K1＝2 000，相应地开环频域特性如图7所示，幅值为5.74 dB，相位裕量40.8°。因开环时系统稳定性最差，加载后系统稳定性会更好一些。

图7 Kv=0.2，K1=2 000时系统开环频域特性Fig.7 Frequency domain characteristic of system open loop when Kvis 0.2 and K1is 2 000

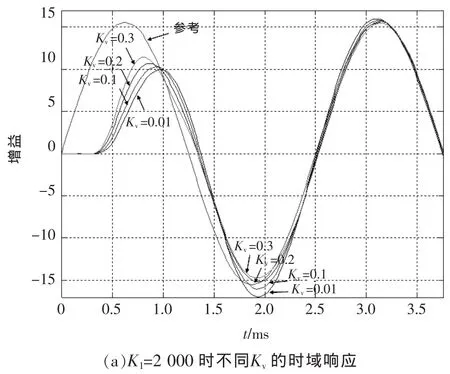
为了比较比例参数Kv和谐振参数K1对系统性能的影响，分别取不同的Kv和K1，相应的时域响应曲线如图 8所示。当 K1＝2 000时，Kv分别取0.01、0.1、0.2、0.3时，根据传递函数可画出系统对正弦信号的响应曲线如图8（a）所示，正弦信号有效值为11。由图8可以看出，随着Kv增大，输出电压响应速度增快，稳态误差更小。当Kv取值较小时，在第1个波谷处会出现过冲，Kv越小，过冲越大。当Kv超过 0.4 后，系统变得不稳定。 当 Kv＝0.2，K1分别取 500、1 000、2 000、3 000 时， 系统响应曲线如图8（b）所示。由图可以看出，随着K1增大，输出电压响应速度变快。当K1＝3 000时，在1.5个基波周期内即可达到稳定，稳态误差近似为零；当K1＞3 000时，系统稳定性变差，并逐渐变得不稳定。

4 实验验证

选取相应的控制参数，对理论分析进行实验验证。开关频率5.6 kHz，开关死区1 μs，没有进行死区补偿，参考电压有效值为11 V。当K1＝2 000，Kv分别取0.01、0.1、0.2、0.3时，系统输出电压启动波形如图9所示。随着Kv增大，输出电压响应速度增快，在第1个波谷处出现的过冲越小，与理论分析一致。但理论分析中当Kv取0.2和0.3时，不存在过冲，而实验中仍存在比较明显的过冲，这是因为，理论分析是基于3阶Pade近似得到的。由分析可知，系统采用3阶Pade近似时的时域响应曲线和实际还是有一些差别，所以实验结果和理论分析的波形不完全一致。实验中，Kv取值不宜比0.3大，否则系统稳定性会变差并逐渐变得不稳定。

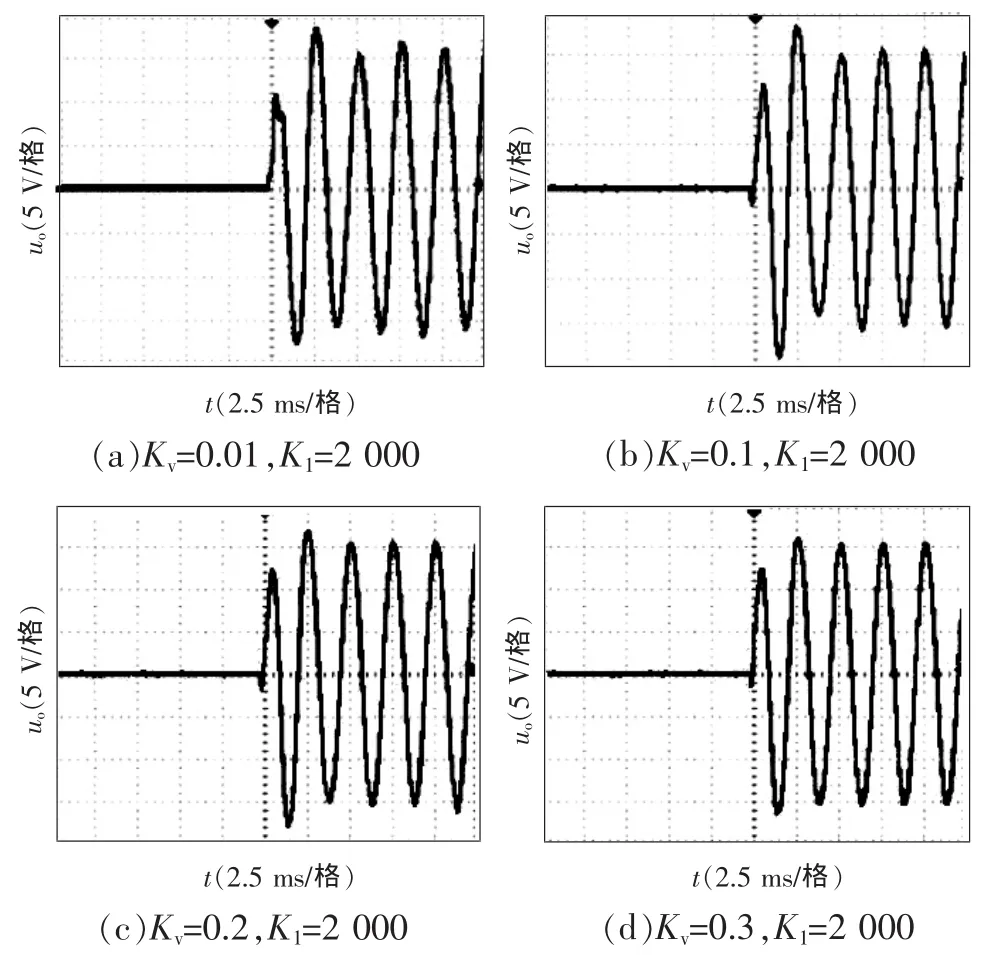
图9 K1＝2 000时Kv变化时空载启动电压波形比较Fig.9 uowaveforms with Kvchanging when K1is 2 000

当 Kv＝0.2，K1分别取 500、1 000、2 000、3 000时，系统输出电压的启动波形如图10所示。随着K1增大，输出电压响应速度增快，当K1＝2 000时，在2个基波周期内即可达到稳定，但出现了过冲。当K1＝3 000时，系统稳定性已经很差了。

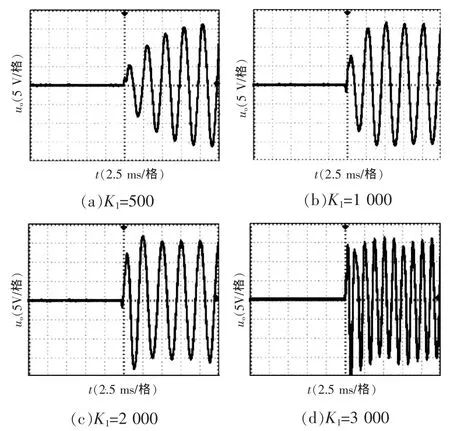
图10 Kv＝0.2时K1变化时空载启动电压波形比较Fig.10 uowaveforms with K1changing when K1is 0.2

图11 Kv=0.2，K1=2 000时uo谐波含量分析Fig.11 uoharmonic analysis when Kv is 0.2 and K1is 2 000

当 Kv＝0.2，K1＝2 000 时， 系统带 2 Ω 电阻负载稳定后的谐波含量分析如图11所示。输出电压THD为2.29%，和设计要求相一致。由于死区的影响，3次谐波的含量较大，若采用合适的死区补偿方法，可以减小死区对低次谐波的影响，输出电压的THD会更小一些。

系统突加突减负载时的波形如图12所示。由图可见，突加负载时，系统在2.5个周期内可以恢复到稳态；突减负载时，1个基波周期内可恢复到稳态。在突加和突减负时，电压会出现突变，突变小于2 V。系统具有较好的动态性能。

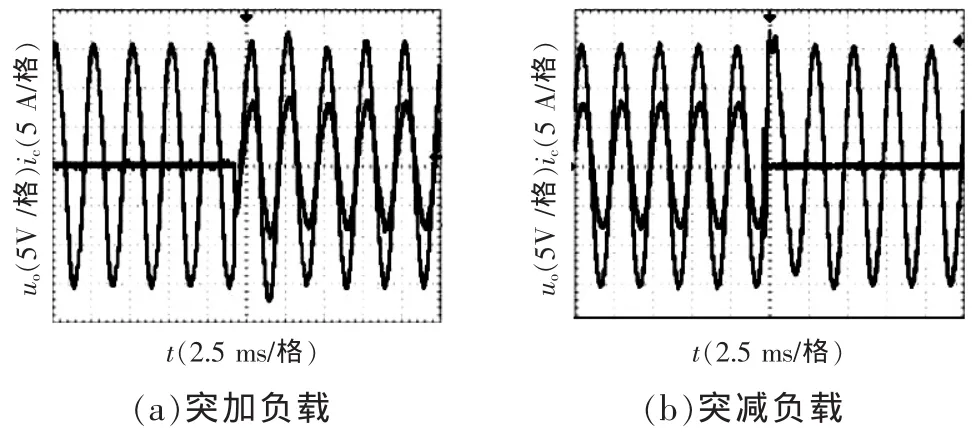
图12 Kv=0.2，K1=2 000时电压电流波形Fig.12 Waveforms of output voltage and current when Kvis 0.2 and K1is 2 000

5 结语

中频逆变系统的基波频率远大于工频系统，因此相同的延时在中频逆变系统中会有更大的影响。当采用传统的频域方法设计系统控制参数时，可通过对延时环节进行线性化近似，以保证控制系统具有合适的相角裕度。对于400 Hz系统，当延时较大时，可以采用3阶Pade近似；延时较小时，可以采用2价Pade近似。

[1]Mihalache L.DSP Control of 400 Hz Inverters for Aircraft Applications[C].37th IAS Annual Meeting.2002：1564-1571.

[2]Mihalache L.Improved Load Disturbance Rejection Method for 400Hz GPU Inverters[C].IEEE APEC’04,2004：95-101.

[3]谢孟，蔡昆，胜晓松，等.400 Hz中频单相电压源逆变器的输出控制及其并联运行控制[J].中国电机工程学报，2006，26（6）：78-82.Xie Meng,Cai Kun,Sheng Xiaosong,et al.Output control and parallel operation control of 400 Hz single-phase voltage-source inverter[J].Proceedings of the CSEE,2006,26（6）：78-82（in Chinese）.

[4]李子欣，王平，李耀华，等.采用数字控制的400 Hz大功率逆变电源[J].中国电机工程学报，2009，29（6）：36-42.Li Zixin,Wang Ping,Li Yaohua,et al.400 Hz high-power voltage-source inverter with digital control[J].Proceedings of the CSEE,2009,29（6）：36-42（in Chinese）.

[5]蔡昆，李耀华，胜晓松，等.高性能单相电压源逆变器的输出控制[J].电工技术学报，2005，20（1）：104-107.Cai Kun,Li Yaohua,Sheng Xiaosong,et al.Output control of the high performance voltage source inverters[J].Transactions of China Electrotechnical Society,2005,20 （1）：104-107（in Chinese）.

[6]李剑，康勇，陈坚.400 Hz恒压恒频逆变器的一种模糊-重复混合控制方案[J].中国电机工程学报，2005，25（9）：54-61.Li Jian,Kang Yong,Chen Jian.A hybrid fuzzy-repetitive control scheme for 400 Hz CVCF inverters[J].Proceedings of the CSEE,2005,25（9）：54-61（in Chinese）.

[7]葛红娟，蒋华，王培强.基于内模原理的新型三相航空静止变流器闭环控制系统[J].电工技术学报，2006，21（9）：88-92.Ge Hongjuan,Jiang Hua,Wang Peiqiang.a novel threephase aviation static inverter closed-loop control system based on the internal model principle[J].Transactions of China Electrotechnical Society,2006,21 （9）：88-92（in Chinese）.

[8]唐诗颖，彭力，康勇.脉宽调制逆变电源数字双环控制技术研究[J].中国电机工程学报，2009，29（15）：55-60.Tang Shiying,Peng Li,Kang Yong.Research on dual-loop digital control technique for pulse width modulation inverters[J].Proceedings of the CSEE,2009,29 （15）：55-60（in Chinese）.

[9]单鸿淘，彭力，孔雪娟，等.数字化过程对脉宽调制逆变电源性能的影响机理[J].中国电机工程学报，2009，29（6）：29-35.Shan Hongtao,Peng Li,Kong Xuejuan,et al.Effect of digital process on the performance of pulse width modulation inverter[J].Proceedings of the CSEE,2009,29（6）：29-35（in Chinese）.

[10]刘春喜，孙驰，高姬.SPWM方法对系统延时的影响[J].电力系统自动化设备，2013，33（6）：75-80.Liu Chunxi,Sun Chi,Gao Ji.Effect of digital SPWM on system delay[J].Electric Power Automation Equipment，2013，33（6）：75-80（in Chinese）.

[11]王成山，石颉.考虑时间延迟影响的电力系统稳定器设计[J].中国电机工程学报，2007，27（10）：1-6.Wang Chengshan,Shi Jie.PSS Designing with consideration of time delay impact[J].Proceedings of the CSEE,2007,27（10）：1-6（in Chinese）.

[12]刘春喜，马伟明，孙驰，等.大功率400Hz逆变电源数字控制设计研究[J].电工技术学报，2011，26（1）：100-107.Liu Chunxi,Ma Weiming,Sun Chi,et al.Digital control design of high power 400 Hz inverters[J].Transactions of China Electrotechnical Society，2011，26 （1）：100-107（in Chinese）。