低渗透油藏反九点井网水驱前缘研究
2015-12-28朱圣举张皎生安小平
朱圣举 朱 洁 张皎生 安小平
(1.中国石油长庆油田分公司勘探开发研究院,西安 710018;2.低渗透油气田勘探开发国家工程实验室,西安 710018;3.长安大学地球科学与资源学院,西安 710054)
水驱油过程中,前缘含水饱和度所处的位置就叫水驱前缘,它是研究水驱开发油藏油水运动规律的重要因素之一。对于水驱前缘的研究,有的文献采用试井理论分析方法[1-2],这种方法不能有效描述实际水驱规律;有的文献采用动态监测方法[3-4],这种方法成本较高;有的文献采用油藏工程计算和数值模拟方法[5-8],这种方法可以有效描述水驱规律,但没有延伸到反九点面积注采井网的水驱前缘运动规律问题。
本次研究基于低渗透油藏水驱理论,建立低渗透油藏反九点井网的水驱前缘计算模型,通过三角变换方法,给出水驱前缘图的绘制方法和步骤。根据鄂尔多斯盆地某低渗透油藏的实际资料进行计算,对模型与实际结果的一致性加以验证。
1 水驱前缘模型
反九点井网中1个注采井组可以划分为16个渗流单元[9]。如图1所示,其半横轴长度)与半纵轴长度的关系为:图形符号“△”表示注水井,“○”表示采油井;设mL。x、m均为系数,无因次。
对于每一个渗流单元,根据低渗透油藏反九点井网渗流理论[9],水驱前缘位置分别由2个函数来描述:Lf1和 Lf2。
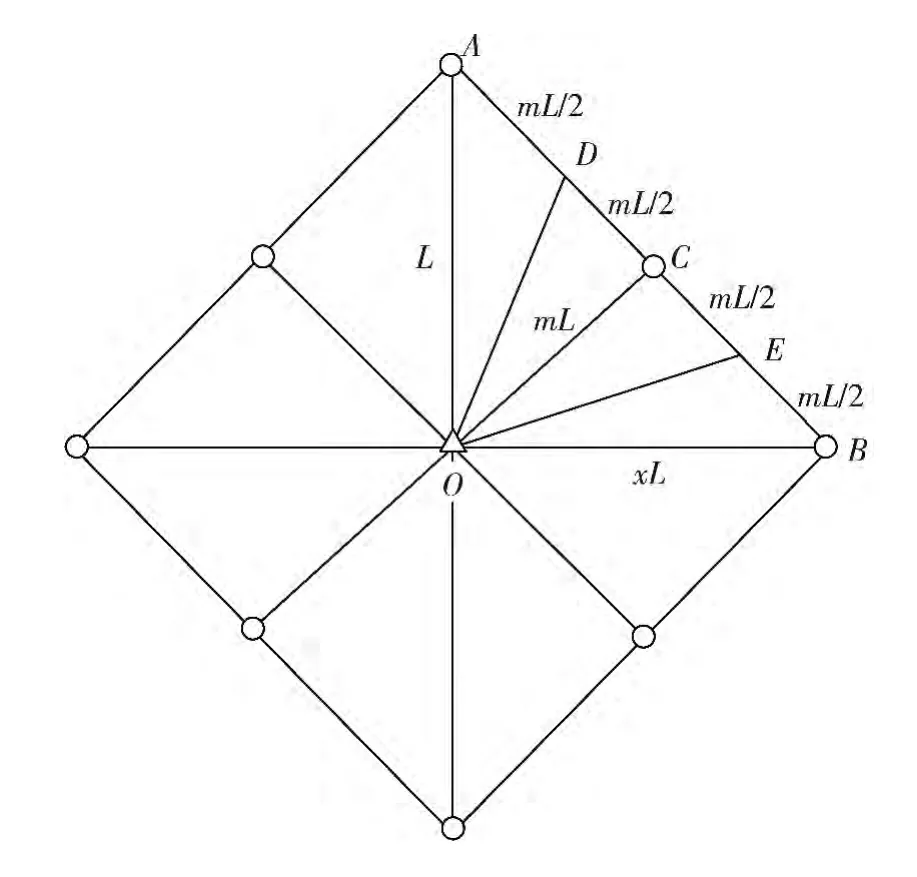
图1 反九点井网渗流单元划分示意图
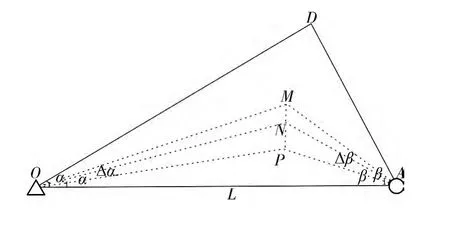
图2 三角形OAD渗流单元图
在渗流单元△OAD中,不同角度的水驱前缘达到图2中N 处的时间为 t1(α)[9]:

式中:α、β — 角变量,rad;
K— 储层渗透率,10-3μm2;
μ—地层流体黏度,mPa·s;
λ—启动压力梯度,MPa/m;
ph—注水井井底流压,MPa;
pf—采油井井底流压,MPa;
L— 流线长度,即流管中线,m;
rw— 井筒半径,m;
f'w(Swf)—前缘含水饱和度Swf对应的含水率变化率;
φ—储层孔隙度;
t1(α)—不同角度的水驱前缘达到图2中N处时的时间,d。
当α趋近于0时,得水驱前缘沿注采井连线OA到达N处对应的时间t1[9]:
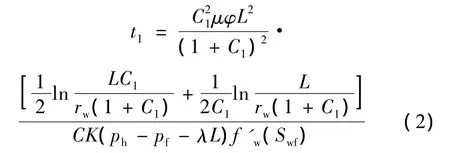
不同角度的水驱前缘到达生产井底A时的时间t2(α)[9]:
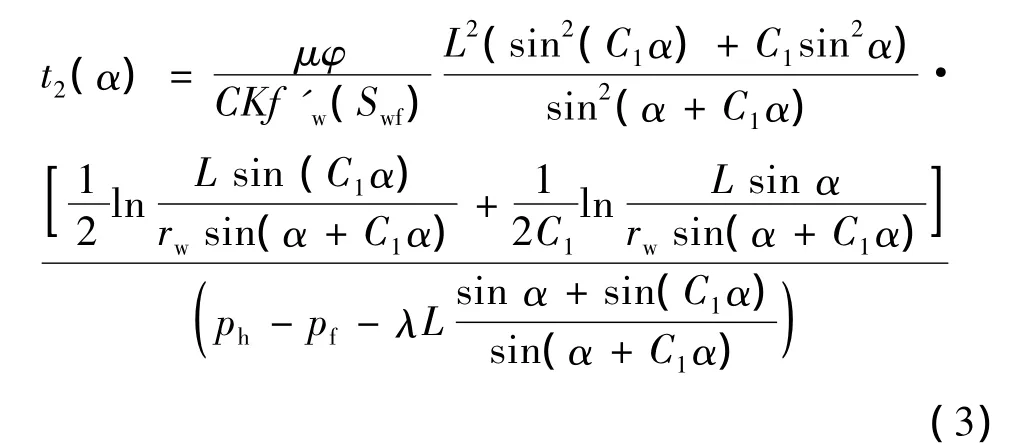
当α趋近于0时,得水驱前缘沿注采井连线OA到达生产井底A处的时间t2[9]:
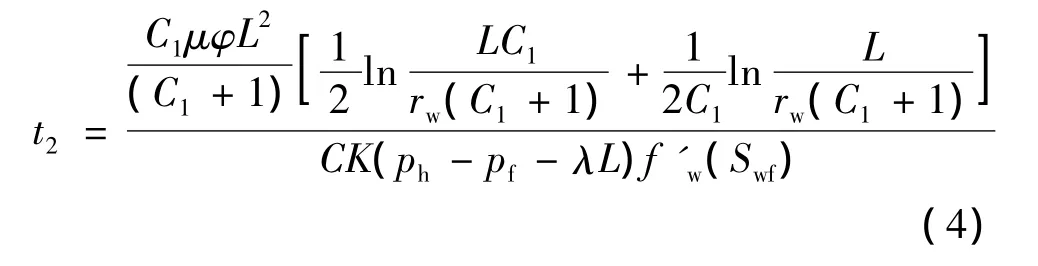
非达西渗流中一定存在启动压力梯度,在相应的井网和注采压差下,整个面积内的流体并不一定都能流动,而是必然有一个启动角α0,启动角由式(5)计算[10]:
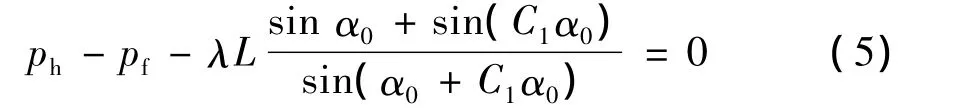
对于任一时间t,可分别在3种不同情况下计算水驱前缘位置:
第一种情况,当t≤t1时,水驱前缘位置函数Lf1为[9]:
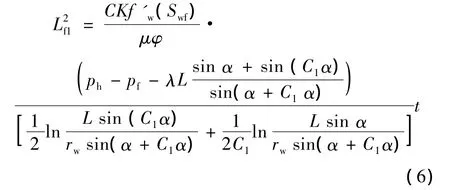
第二种情况,当t1<t≤t2时,可由式(1)确定αm值。在αm<α≤α0处,用油水前缘位置函数Lf1;在α<αm处,用油水前缘位置函数L[9]f2:
第三种情况,当t>t2时,可由式(1)和式(3)分别确定αm值和αn值:在αm<α≤α0处,用油水前缘位置函数Lf1;在αn≤α≤αm处,用油水前缘位置函数Lf2。
2 水驱前缘位置处理方法
在此,以渗流单元△OAD为例进行分析。
(1)先计算出 t1,t2,α0。
(2)对于任一时间t,采用试凑法,计算出与t相对应的αm及αn。
(3)建立直角坐标系,以注水井点为坐标原点,以2条对角线分别为横坐标轴、纵坐标轴,并由函数Lf1及Lf2计算出不同角度α的坐标(x、y)。
对于函数Lf1:

对于函数Lf2, 令:
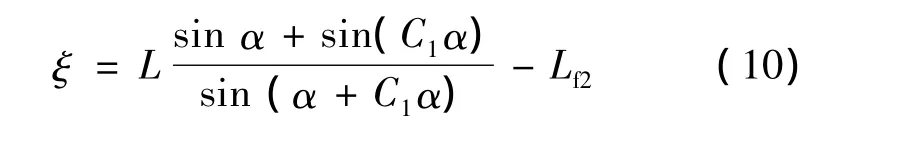
则
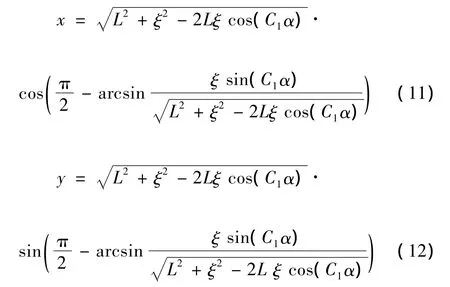
(4)根据不同时间、不同角度的坐标(x,y),绘出水驱前缘图。
3 实例应用分析
鄂尔多斯盆地某低渗透油藏为反九点井网,采用注水开发方式,各项参数如下:C=0.086 4,φ=0.14,f'w(Swf)=1.57,μw=0.5 mPa·s,μo=2.4 mPa·s,K=5.6 × 10-3μm2,λ =0.017 5 MPa/m,L=212 m,rw=0.1 m,C1=2.441,α1=0.321 75 rad,x=1,m =/2,ph-pf=20 MPa。
计算不同时间t的水驱前缘位置。如图3所示,以注水井为中心,由内向外,水驱前缘的时间分别为 100,200,300,400,500,1 000,1 500,2 000,2 500,3 000 d。
由图3可以看出,在等时间距的情况下,水驱前缘等时线分布由疏到密,这说明水驱前缘位置的移动速度发生变化,先快后慢。
该井组在注水井的注水时间长达6 a,共2 230 d。在距注水井120 m的地方钻开1口检查井,图3中图形符号“●”表示检查井,结果显示注入水已驱到此处。而水驱前缘计算结果表明,在t=2 000 d时,水驱前缘到达此处。两者结果相近。
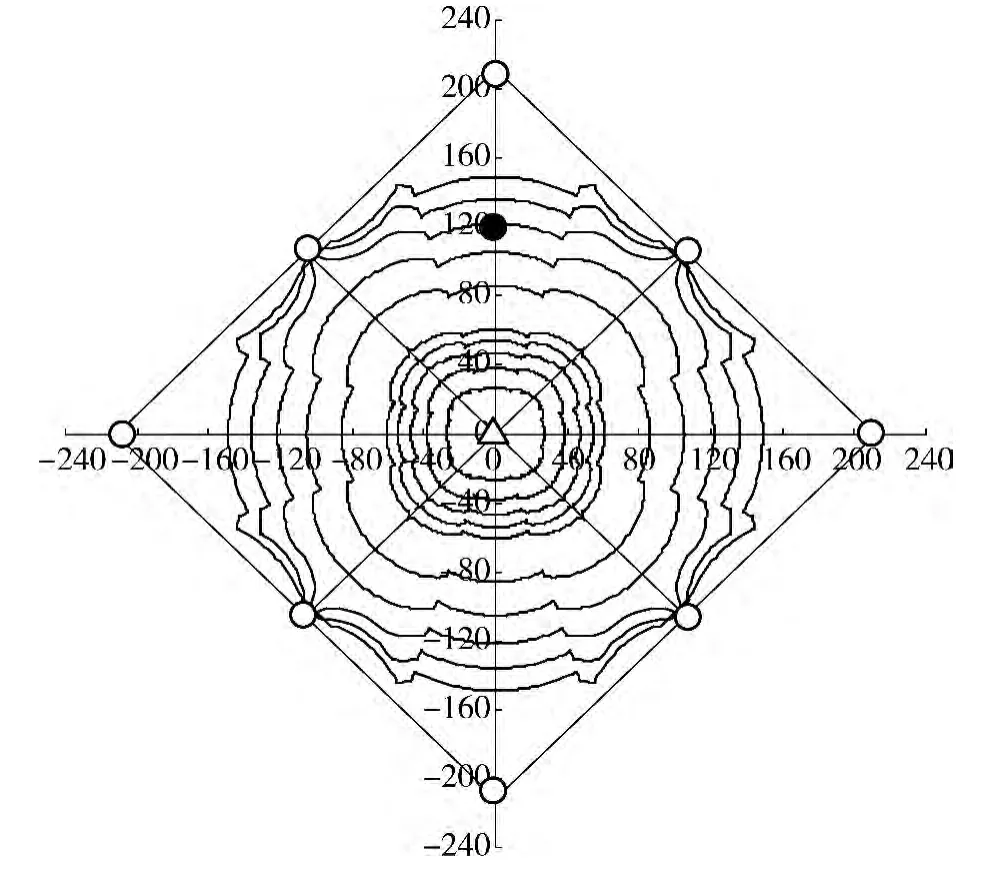
图3 反九点井网不同时间水驱前缘位置图
4 结语
本次研究中运用解析法,首次创立了低渗透油藏反九点井网水驱前缘位置计算方法及绘图步骤,经实践检验,该方法合理可行。研究发现,以注水井为中心,水驱前缘向采油井方向的移动规律是先快后慢。
[1]李星,张公社,曹琴,等.应用试井资料研究水驱油藏剩余油饱和度分布[J].油气井测试,2008,17(2):1-4.
[2]刘佳洁,贾永禄,路建国,等.试井分析确定陆梁油田J2x4油藏水驱前缘变化特征[J].重庆科技学院学报(自然科学版),2010,12(3):34-35.
[3]刘东丰,李小玲,李幸来,等.注水井水驱前缘监测技术及应用[J].中外能源,2008,13(6):51-53.
[4]杨志冬,周金燕,常智勇,等.利用注水前缘监测技术跟踪水推速度[J].中国工程科学,2012,14(4):31-33.
[5]丘勇松,杨正明,李捷,等.低渗透油层注水开发的层间突进研究[J].西安石油学院学报(自然科学版),2003,18(1):27-29.
[6]徐庆岩,杨正明,何英,等.特低渗透多层油藏水驱前缘研究[J].油气地质与采收率,2013,20(2):74-76.
[7]汪全林,柴世超,程自力,等.基于两相流低渗油藏合理注采井距确定方法[J].东北石油大学学报,2012,36(4):45-48.
[8]卜亚辉,姚军,李爱芬,等.三维油藏流动电位数值模拟及油水前缘预测[J].中国石油大学学报(自然科学版),2014,38(1):81-86.
[9]朱圣举,朱洁,安小平,等.低渗透油藏菱形反九点井网面积波及系数研究[J].重庆科技学院学报(自然科学版),2013,15(2):80-84.
[10]计秉玉,李莉,王春艳.低渗透油藏非达西渗流面积井网产油量计算方法[J].石油学报,2008,29(2):256-261.
