等重叠率螺旋线的非球面抛光轨迹规划

曲兴田,王宏一,樊成,吴文征,刘孝龙

(1.吉林大学机械科学与工程学院,130025,长春;2.苏州大学机器人与微系统研究中心,215021,江苏苏州)



等重叠率螺旋线的非球面抛光轨迹规划

曲兴田1,王宏一1,樊成2,吴文征1,刘孝龙1

(1.吉林大学机械科学与工程学院,130025,长春;2.苏州大学机器人与微系统研究中心,215021,江苏苏州)

为改善抛光轨迹以获得更好的加工精度,分析了轨迹在非球面上所产生的去除区域的覆盖情况,并提出了一种等重叠率螺旋线抛光轨迹规划方法。基于赫兹接触理论的去除区域的覆盖情况分析表明,常用的阿基米德螺旋线由于弹性接触变化和投影行距变化导致轨迹间去除区域接触变化,从而不能保证加工精度均匀一致,为此引入了重叠率的概念以量化分析该变化情况。提出的轨迹规划方法分析了重叠率的变化特点,并依据螺旋线的性质建立了螺旋线行距与非球面面形的变化关系,保证了轨迹间去除区域的稳定接触。仿真结果表明,在非球面抛光过程中应用等重叠率螺旋线轨迹,重叠率变化范围从阿基米德螺旋线轨迹的56.1%～26.2%缩小到现在方法的56.1%～55.3%,为非球面抛光的均匀性和一致性奠定了基础。

非球面;抛光;螺旋线轨迹;等重叠率

随着现代光学技术的飞速发展,非球面光学元件的应用已日趋广泛。小工具头抛光技术由于控制准确、抛光灵活性高等优势使加工的精度及效率大幅度提高,成为了非球面光学元件制备的主要手段之一。抛光轨迹规划作为抛光工艺的重要研究方向,直接影响着加工质量、加工时间和使用寿命。因此,通过抛光轨迹的合理规划实现良好的抛光效果就显得尤为重要。对于传统轨迹规划方法已经有大量研究,其基本理论包括参数线法[1-2]、截面线法[3-4]、等残余高度法[5-6]等。这些算法大都针对车削、磨削工艺进行研究,并没有充分考虑小工具头抛光的特点。近年来,相关学者针对小工具头抛光特点建立了很多抛光轨迹规划方法。文献[7]将具有良好的适应性和覆盖性的Peano轨迹应用到抛光领域。文献[8]借鉴质点系平衡的加权平均思想,提出了引入残差分布的轨迹规划方法。文献[9]为消除一般轨迹产生的规则轨迹误差提出了伪随机抛光轨迹。文献[10]针对光栅轨迹抛光提出了行距适应算法增加轨迹在自由曲面上覆盖的均匀性。所以,对于抛光轨迹而言,提高轨迹覆盖的均匀性有助于改善曲面零件的加工质量。

本文通过分析表明,通常使用的阿基米德螺旋线由于抛光时工具头与工件的弹性接触变化和投影行距变化,造成了轨迹产生去除区域在非球面覆盖不均匀,其主要表现在轨迹间去除区域的接触情况变化较大。抛光去除区域内不同位置材料的去除情况不同,轨迹间去除区域接触变化会引起变化的抛光残留。此外,抛光迭代去除模型往往建立在稳定的抛光轨迹间去除区域情况之上。因此,稳定的轨迹间去除区域接触情况就成为了保证非球面均匀一致的加工精度的必要前提。

为此,本文基于赫兹接触理论对螺旋线上去除区域覆盖变化情况进行建模分析,建立了螺旋线与非球面联系,实现了等重叠率的非球面螺旋线轨迹规划方法,保证了加工轨迹产生去除区域分布的均匀一致。

1 抛光接触建模

接触模型建立在赫兹接触理论之上,文献[11-12]将赫兹接触理论应用于小工具头抛光均取得了良好效果。文献[13]指出,在固定行距下,抛光接触区域随着工件曲率变化发生了改变而不能保证恰好完整的覆盖工件。因此,为引入接触区域变化,本文提出以轨迹所产生的去除区域覆盖变化情况来衡量轨迹对加工精度的影响。

1.1 接触区域计算

图1 接触点曲率半径

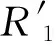
(1)

椭圆的半轴方向与主曲率方向一致,即非球面的经线和纬线方向。半轴长度a和b计算公式如下

(2)

(3)

式中:F代表抛光力;μ1、μ2分别为两个物体的泊松比;E1、E2分别为两个物体的弹性模量;系数m、n与B/A有关,令cosγ=B/A,根据γ值,对应m、n值可由表1插值计算得到,A、B计算方程如下

(4)

(5)

式中:φ代表两个物体在接触点处法面之间的夹角。

表1 m、n参数插值计算表[14]

1.2 非球面上接触区域建模

非球面任意点位置的接触区域可以通过式(1)～式(5)计算而得,但是得到接触区域边界在工件的空间位置仍是一个复杂的过程。接触区域较小,其所在平面接近且几乎平行于接触点切平面。为简化计算,将接触区域放置在接触点在非球面的切平面上,并将接触边界在工件上的投影作为接触区域在非球面上的空间位置。

以非球面的回转轴为z轴、顶点为坐标原点O,建立Oxyz坐标系。如图2所示,以非球面任意经线截面为xz平面。在xz平面的非球面母线方程可表示为

z=a1x+a2x2+a3x3+a4x4+…

(6)

式中:a1、a2、a3、a4为方程系数。那么,接触区域在xy平面的投影可由下式计算

(7)

式中:am、amxy为经线方向接触椭圆半轴;bc、bcxy为纬线方向接触椭圆半轴。式(7)所得区域沿z轴投影到非球面,得到工具头与非球面在接触点的去除区域。距离回转轴相同距离的位置点具有相同的几何性质,非球面其他位置接触建模也可相应求出。

图2 非球面经线截线示意图

2 阿基米德螺旋线仿真与分析

加工中常用的阿基米德螺旋线轨迹的极坐标形式可表示为

r=kθ

(8)

式中:k为控制螺旋线间距的参数,螺旋线在径向上等间距。由于螺旋线和非球面的连续性,仅对过回转轴的一侧截面轨迹间去除区域变化情况进行分析,可以代表整体变化情况。相关仿真数据见表2,所用抛光力F=8 N。

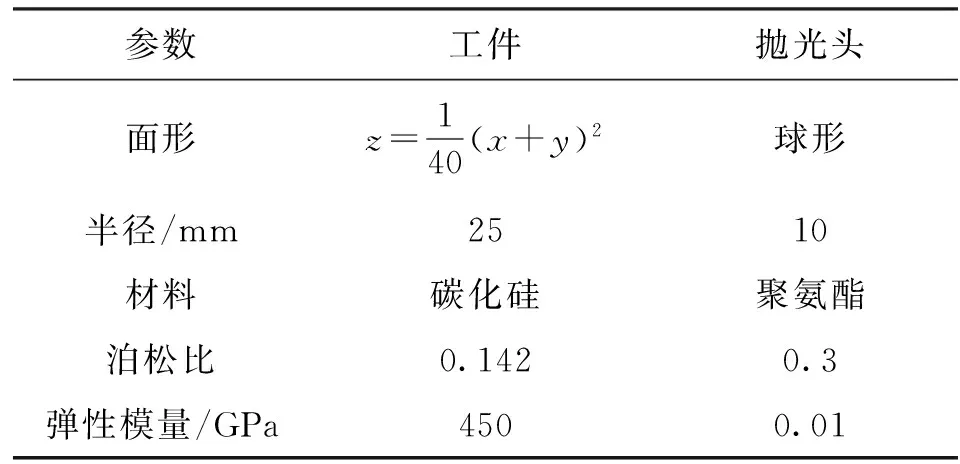
表2 接触模型仿真数据

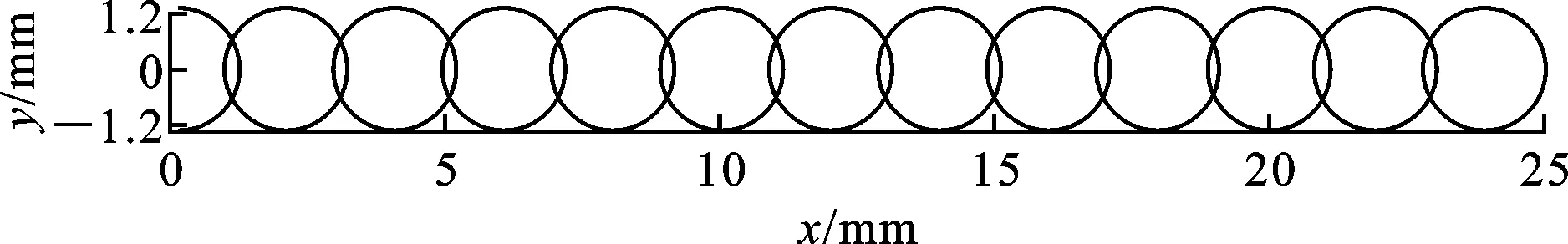
图3 去除区域的渐变情况

图3为去除区域在非球面上从中心到边缘的渐变情况,可见由于非球面曲率变化,不同位置去除区域并不一致。此外,由于非球面陡度变化引起投影后阿基米德螺旋线实际行距也发生了变化。两方面因素共同造成了阿基米德螺旋线轨迹间去除区域接触的变化。实际行距s计算公式如下

(9)

(10)

行距为2时阿基米德螺旋线在非球面上轨迹间去除区域接触情况见图4a。图5a为去除区域在xy平面的投影。轨迹间去除区域在回转中心附近相互重叠,到边缘去除区域相互之间已有较大间隙。这样在靠近非球面边缘处轨迹间已经出现了未加工的区域,显然造成了加工精度的下降和不一致,同时即使靠近中心区域满足精度要求,为避免未加工区域也要缩小行距,降低了加工效率。

(a)行距为2 (b)行距为1图4 阿基米德螺旋线去除区域的接触情况

图4b、图5b为行距为1时截面上的去除区域情况,可见在回转中心附近,轨迹间去除区域重叠较多,在边缘处重叠部分较少。为量化这一变化,本文引入重叠率的概念

(11)

(a)行距为2

式中:an-1、an为加工轨迹径向相邻轨迹点接触椭圆经线方向半轴;si为径向相邻轨迹点距离。重叠率与si位置定义在an轨迹点位置。

(b)行距为1图5 接触区域在xy平面的投影

行距为1时的重叠率变化情况见图6,重叠率从回转轴附近的56.1%逐渐下降到26.2%。如图6所示,即使采用较小行距,轨迹间去除区域变化依然较大。

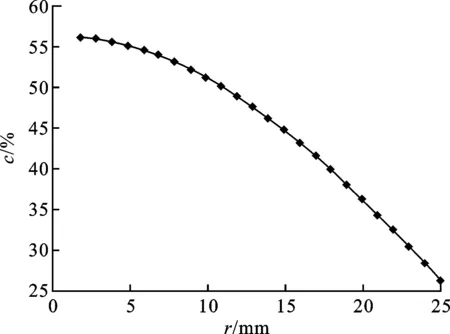
图6 行距为1时的重叠率变化情况

抛光加工精度可分为表面粗糙度与面形精度两个方面。轨迹间去除区域接触变化往往造成抛光残留变化引起非球面上表面粗糙度不一致,也为保证上一道工序的面形精度增加了不确定因素。此外,去除区域接触情况与其他抛光参数设定密切相关,变化的去除区域接触情况使得抛光难以维持在一个良好的抛光工艺组合上,造成了加工精度与效率的下降。因此,所采用螺旋线有必要根据所加工非球面面形进行变化,以保证非球面上稳定一致的轨迹间去除区域接触情况。

3 等重叠率螺旋线轨迹规划

为保证轨迹间去除区域的稳定接触,本文对阿基米德螺旋线进行了改进。通过建立螺旋线与投影行距变化和弹性接触变化的关系,实现了螺旋线的有效控制,使重叠率保持稳定。

由于回转型非球面距离回转轴相同位置r具有相同的几何性质,且螺旋线中心与回转轴重合,即r可以代表螺旋线极径长度。因此,建立螺旋线平面行距变化与r的关系,分析影响重叠率变化的因素,并通过r构建两者的联系,实现等重叠率的螺旋线轨迹规划。

3.1 螺旋线行距控制

螺旋线可以看作一点P的运动轨迹,这时P绕中心点O以等角速度旋转的同时,P点沿动射线OP以速度v远离中心点。当速度v为常数(v=k)时,该螺旋线为阿基米德螺旋线。由于螺旋线径向相邻点对应角度变化均为2π,因此平面上径向相邻点Pn-1、Pn的距离b(即行距)为

(12)

从式(12)可以观察到,v与b有着近似的等比例变化关系,即通过改变v可以近似控制螺旋的行距变化,从而改变轨迹间去除区域的接触。因此,引进关于r的速度变化函数将阿基米德螺旋线v=k变为

v=d(r)k

(13)

由式(12)、式(13)得到近似行距控制如下

b(r)=d(r)2πk

(14)

3.2 等重叠率螺旋线实现

由于行距值较小,轨迹间相邻点接触椭圆半轴值接近。由ai-1≈ai,式(11)可以化简为

(15)

由此重叠率变化主要由位置点实际行距与经线方向半轴长度比值变化产生。下面,确定d(r)应有的变化关系,以使两者比值不发生变化。

如图7所示,以非球面顶点为原点,建立非球面母线的Oxy坐标系。从原点O开始,在非球面上离散点P0,P1,P2,…,Pn。离散点水平间距b相等,b值与基础螺旋线相关,b=2πk。

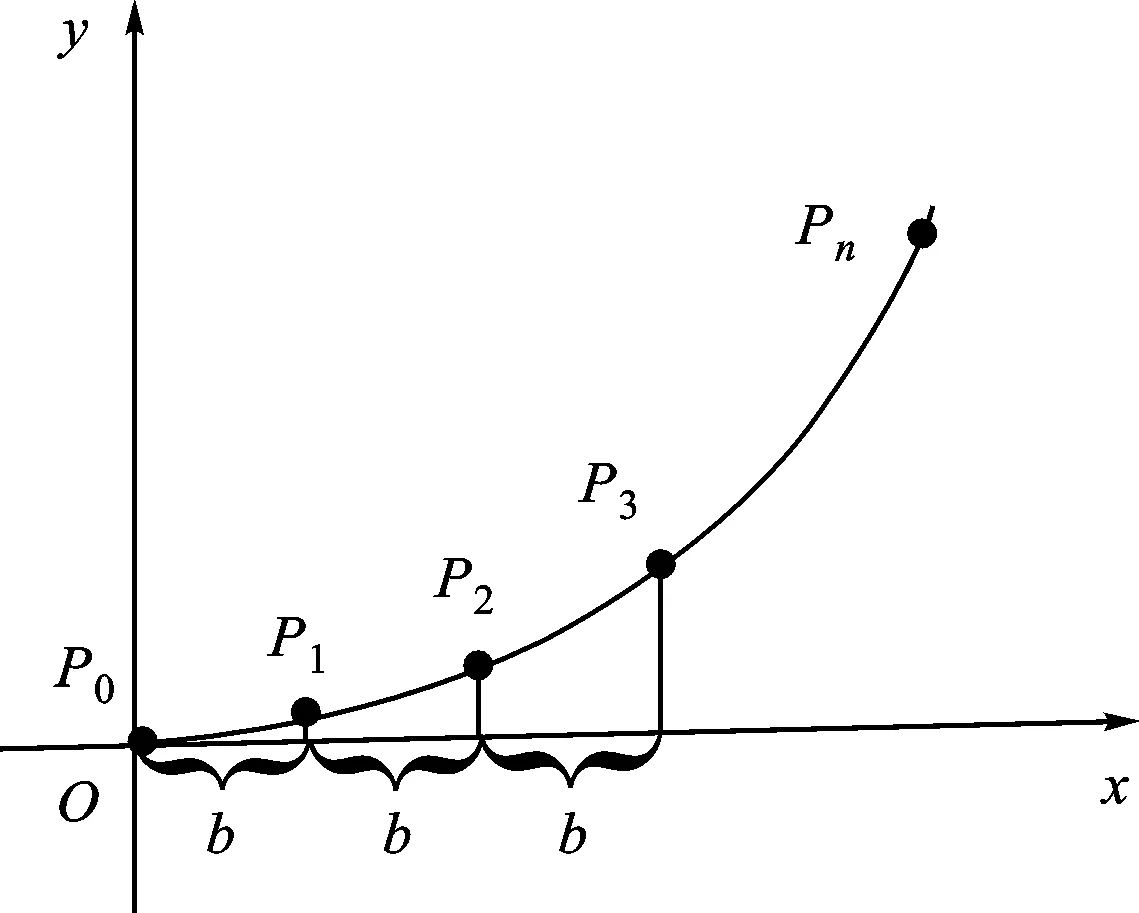
图7 离散点选取示意图

为使si/ai不发生变化,则Pi点处应有如下关系

(16)

式中:bi为螺旋线在Pi点处应有行距;a0、ai分别为P0、Pi点处经线方向半轴长度;hi=si/b为投影变化比。由式(2)、式(16)可导出

(17)

式中:m0、mi为对应点在式(2)中计算得到的m值;A0、Ai为对应点在式(2)中计算得到的A值。由式(14)变化关系,d(r)可由求得离散点经多项式拟合得出

(18)

由式(18)可知,Ai、mi仅与对应点主曲率变化相关,hi变化仅与基础行距b和非球面面形相关,且基础行距b对d(r)影响很小,只需根据常用行距进行选取。在使用不同行距时无需改变b,这样速率变化函数d(r)仅与非球面面形与抛光头曲率变化相关。当改变非球面材质、抛光力等参数时,等重叠率螺旋线并不发生变化。

如上建立的质点径向运动速率v与r的变化关系,则质点运动到r位置时,平均速度为

(19)

由此,改变后的螺旋线方程由r=kθ变为

(20)

显然,在回转轴处c(r)=1。在实际加工中,螺旋线轨迹离散为密集的点(q1,q2,q3,…,qn),相邻点离回转轴距离接近。因此,变化后的螺旋线上的点可迭代求出,计算公式如下

(21)

4 实 例

根据等重叠率螺旋线轨迹规划方法,重新生成表2数据的加工轨迹。

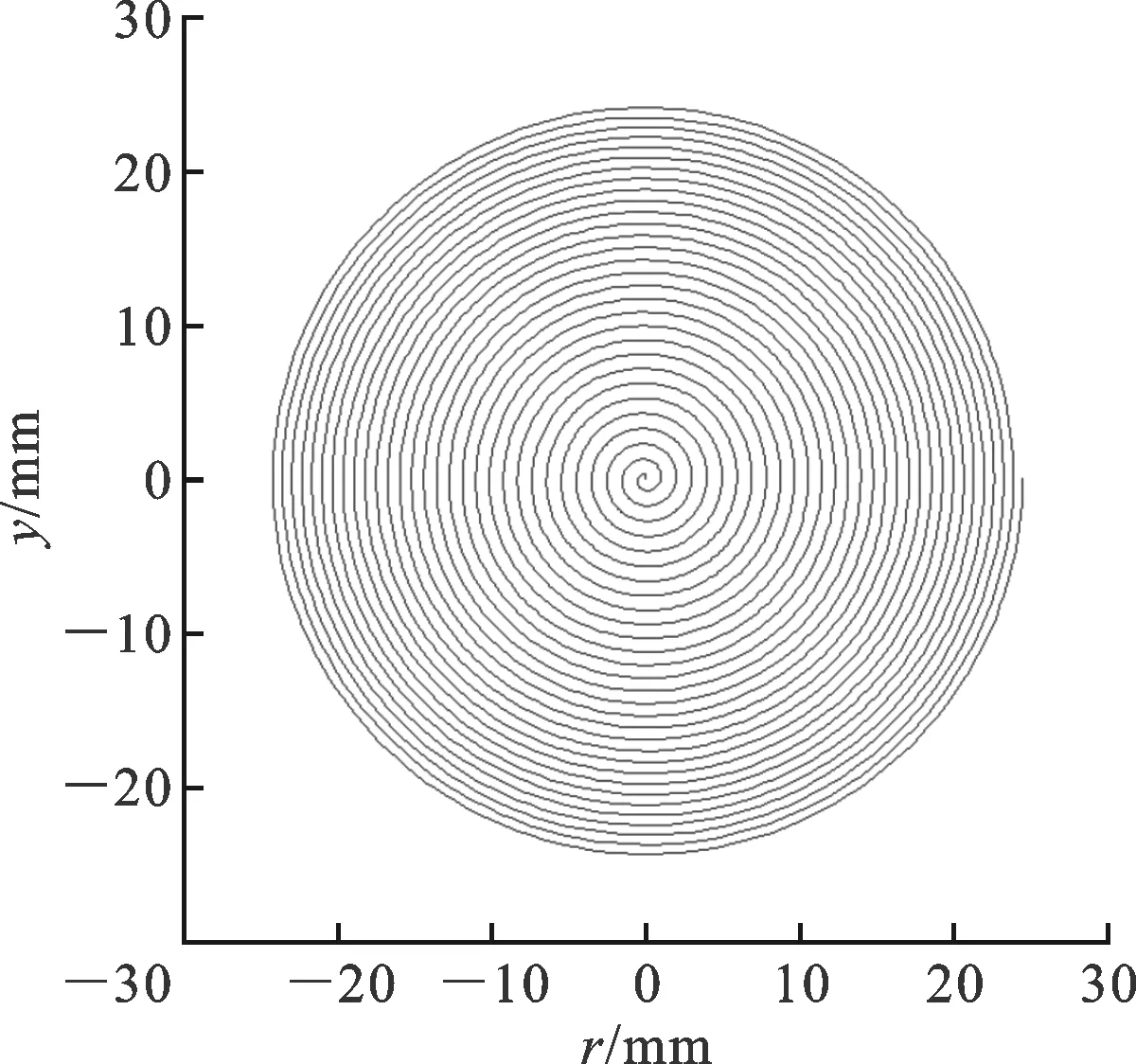
图8 等重叠率时的螺旋线轨迹

对行距为1的阿基米德螺旋线改变后的螺旋线轨迹见图8。改变后螺旋线根据极径变化调整行距,从图中可以观察到,变化后螺旋线从中心靠近边缘逐渐收窄。

行距为1的阿基米德螺旋线改变后螺旋线轨迹间去除区域情况如图9a、图10a所示,轨迹间去除区域接触情况基本一致。图11为改变前后重叠率变化对比,改变后重叠率变化控制在56.1%与55.3%之间。

(a)行距为1 (b)行距为2图9 等重叠率螺旋线去除区域接触情况

(a)行距为1

(b)行距为2图10 等重叠率螺旋线去除xy平面的投影

行距为2的阿基米德螺旋线改变后螺旋线轨迹间接触区域情况如图9b、图10b所示,可见得到了稳定的轨迹间去除区域接触。

变化后螺旋线保证了轨迹间去除区域的稳定接触,为均匀一致的加工精度奠定了良好基础。在本节,对非球面应用两种不同的行距均取得了良好的效果,验证了算法的有效性。

图11 两种方法重叠率的对比

5 结 论

(1)由于抛光头与非球面接触区域变化和投影行距变化,阿基米德螺旋线轨迹间去除区域接触情况变化较大,不能保证均匀一致的加工精度。

(2)以去除区域在非球面上的覆盖情况衡量轨迹对加工精度的影响,并提出了重叠率的概念,量化了去除区域覆盖变化情况。

(3)采用等重叠率螺旋线轨迹算法,保证了非球面上稳定的去除区域覆盖情况,为均匀一致的加工精度奠定了基础。通过仿真验证了算法的有效性,重叠率变化范围从改变前的56.1%～26.2%缩小到改变后的56.1%～55.3%。

[1]LEI M, BIN H.Iso-parametric CNC tool path optimization based on adaptive grid generation [J].The International Journal of Advanced Manufacturing Technology, 2009, 41(5): 538-548.

[2]吴福忠, 柯映林.组合曲面参数线五坐标加工刀具轨迹的计算 [J].计算机辅助设计与图形学学报, 2003, 15(10): 1247-1252.

WU Fuzhong, KE Yinglin.Iso-parametric tool-path planning for five-axis compound surface machining [J].Journal of Computer-Aided Design & Computer Graphics, 2003, 15(10): 1247-1252.

[3]FENG H, TENG Z.Iso-planar piecewise linear NC tool path generation from discrete measured data points [J].Computer-Aided Design, 2005, 37(1): 55-64.

[4]樊文刚, 王小椿, 姜虹, 等.一种开阔自由凹曲面五坐标加工多点刀位算法 [J].西安交通大学学报, 2010, 44(9): 69-73.

FAN Wengang, WANG Xiaochun, JIANG Hong, et al.Multi-point tool positioning strategy for five-axis machining of open sculptured concave surfaces [J].Journal of Xi’an Jiaotong University, 2010, 44(9): 69-73.

[5]LEE Y S.Non-isoparametric tool path planning by machining strip evaluation for 5-axis sculptured surface machining [J].Computer-Aided Design, 1998, 30(7): 559-570.

[6]王太勇, 张志强, 王涛, 等.复杂参数曲面高精度刀具轨迹规划算法 [J].机械工程学报, 2007, 43(12): 109-113.

WANG Taiyong, ZHANG Zhiqiang, WANG Tao, et al.High precision tool path planning algorithm for complex parametric surface [J].Chinese Journal of Mechanical Engineering, 2007, 43(12): 109-113.

[7]MIZUGAKI Y, SAKAMOTO M, SATA T.Fractal path generation for a mental-mold polishing robot system and its evaluation by the operability [J].CIRP Annals: Manufacturing Technology, 1992, 41(1): 531-534.

[8]邓伟杰, 郑立功, 史亚莉, 等.离轴非球面数控抛光路径的自适应规划 [J].光学精密工程, 2009, 17(1): 65-71.

DENG Weijie, ZHENG Ligong, SHI Yali, et al.Adaptive programming algorithm for generating polishing tool-path in computer controlled optical surfacing [J].Optics and Precision Engineering, 2009, 17(1): 65-71.

[9]DUNN C R, WALKER D D.Pseudo-random tool paths for CNC sub-aperture polishing and other applications [J].Optics Express, 2008, 16(23): 18942-18949.

[10]TAM H, LUI C, CK MOK A.Robotic polishing of free-form surfaces using scanning paths [J].Journal of Materials Processing Technology, 1999, 95(1): 191-200.

[11]ROSWELL A, XI F J, LIU G.Modelling and analysis of contact stress for automated polishing [J].International Journal of Machine Tools and Manufacture, 2006, 46(3): 424-435.

[12]FAN C, ZHAO J, ZHANG L, et al.Predictive models of the local and the global polished profiles in deterministic polishing of free-form surfaces [J].Proceedings of the Institution of Mechanical Engineers: Part B Journal of Engineering Manufacture, 2014, 228(8): 868-879.

[13]ROSOSHANSKY M, XI F, LI Y.Coverage based tool path planning for automated polishing using contact stress theory [J].Journal of Manufacturing Systems, 2011, 30(3): 144-153.

[14]徐芝纶.弹性力学 [M].北京: 人民教育出版社, 1990: 299-302.

(编辑 杜秀杰)

Uniform-Overlap-Rate Spiral Path for Aspheric Polishing

QU Xingtian1, WANG Hongyi1, FAN Cheng2, WU Wenzheng1, LIU Xiaolong1

(1.Institute of Mechanical Science and Engineering, Jilin University, Changchun 130025, China;2.Robotics and Microsystems Centre, Soochow University, Suzhou, Jiangsu 215021, China)

To improve the polishing path and obtain better machining accuracy, the removal area generated by path on aspheric surface is analyzed, and a novel spiral tool path planning with uniform-overlap-rate is proposed.The removal area analysis following Hertz contact theory shows that the generally used Archimedes spiral fails to ensure the uniform and consistent machining accuracy due to varying contact of the removal area brought from changed elastic contact and projection path interval.Thus the concept of overlap rate is introduced to quantitatively describe the varying contact.The characteristics of varying overlap rate are revealed in the proposed path planning, and the changing relation between spiral and aspheric surface is established to guarantee the stable contact of the removal area between adjacent tool paths.The simulation shows that the range of overlap rate decreases from 56.1%-26.2% for Archimedes spiral path to 56.1%-55.3% for the proposed uniform-overlap-rate spiral path in aspheric surface polishing.

aspheric; polishing; spiral tool path; uniform overlap rate

2014-08-12。 作者简介:曲兴田(1962—),男,教授;吴文征(通信作者),男,讲师。 基金项目:国家重点基础研究发展计划资助项目(2011CB706702)。

时间:2015-04-21

http:∥www.cnki.net/kcms/detail/61.1069.T.20150421.1711.002.html

10.7652/xjtuxb201506020

TH161

A

0253-987X(2015)06-0126-06