自仿射接触点及其在分形接触理论中的应用
2015-12-27周安安陈天宁王小鹏奚延辉
周安安,陈天宁,王小鹏,奚延辉
(西安交通大学机械工程学院,710049,西安)
自仿射接触点及其在分形接触理论中的应用
周安安,陈天宁,王小鹏,奚延辉
(西安交通大学机械工程学院,710049,西安)
为了深入研究分形方法在接触理论中的应用,利用数值模拟实验研究了分形粗糙表面的接触机理,并提出了自仿射接触点的概念。该概念充分利用分形函数自仿射的优点,改善了传统分形接触理论中微凸体不满足分形特性的缺陷,去除了接触理论中微凸体相互作用无法考虑等假设。将自仿射概念应用于分形接触理论中,建立了新的接触模型。模型基于粗糙表面均为各向同性的无润滑表面且可以利用W-M函数模拟的假设,利用接触中接触点最大变形量与接触面积的关系,对分形接触模型进行修正,得到更符合实际情况的分形接触理论。与经典的统计及分形接触模型进行对比,结果表明:G-W模型是一个弹性模型,较少考虑塑性接触,因此G-W模型在整体上会低估粗糙表面的接触压力;M-B模型利用单个余弦函数模拟微凸体,得到的最大接触变形量偏小,且微凸体尺寸分布函数的使用也不准确,M-B模型高估了接触压力;提出的基于自仿射接触点的分形接触模型利用自仿射接触点代替微凸体进行理论推导,能更准确地计算出接触压力;在相同的接触面积下,粗糙表面分形维数越大或分形特征尺度越小,接触压力越小。
接触理论;数值模拟;分形;微凸体
在过去的几十年中,接触机理的研究一直贯穿在各个领域中,如物理(包括机械、电、磁和热等)、化学及生物研究等[1]。在此期间,很多学者提出了不同的接触模型,文献[2]创造性地将微凸体的高度分布与赫兹接触理论结合,推导了整个粗糙表面上的弹性接触模型(G-W模型)。此后,有很多学者基于G-W模型推导了一系列优化模型[3-5],但值得注意的是,G-W模型所使用的统计参数如表面粗糙度等对测量仪器的分辨率有很大的依赖性,所以不能对粗糙表面进行唯一表征,导致接触模型也不唯一。因此,在证明了粗糙表面在一定尺度内满足分形特性后[6-7],文献[8]将分形理论引入接触理论的研究中,推导了分形接触理论(M-B模型)。M-B模型自从被提出后,就引起很多争议,如很多学者意识到M-B模型中假设每个微凸体都完全变形是不正确的,因此文献[9]改进了M-B模型,认为每个微凸体的变形量都可以是从0到最大变形量中的任意一个(M-E模型)。但是,M-E模型仅仅是单个微凸体的接触模型,故文献[10]利用M-E模型的方法推导了整个接触表面上的接触模型。本文研究发现M-B模型中还有一个严重的问题未被意识到:M-B模型利用著名的Weierstrass-Mandelbrot函数(W-M函数)模拟粗糙表面,并基于Hertz接触理论推导接触点上的压力和接触面积的关系,但却仅仅用W-M函数中波长为l的余弦函数代表微凸体,该做法与分形的理念相违背。事实上,分形粗糙表面的任意接触点都应该是自仿射的,即经过放大后,会有更多细节被观察到。特别地,对于由W-M函数模拟生成的粗糙表面,每个接触点都应该由多个余弦函数叠加而成。另外,在M-B模型中微凸体尺寸分布函数的使用也不准确。
因此,本文采用数值实验的方法研究粗糙表面的接触点,并提出一个新的、更加准确的接触点的概念——自仿射接触点,并将其应用到分形接触理论中,推导出更符合分形定义的接触理论。
1 数值模拟
本文的目的是通过数值仿真研究粗糙表面的分形特性,然后利用此特性修正分形接触理论。首先采用多种不同的分形曲线验证经典的Korcak经验法则,然后进一步研究粗糙接触表面上各个接触点的接触面积与该接触点最大变形量的关系。
1.1 海岛面积与个数的Korcak法则验证
分形接触理论的研究中广泛地应用了文献[11]中提出的Korcak经验法则,即面积大于a的岛屿的个数服从以下规律
N(A>a)=Nca-B
(1)
式中:B为和岛屿轮廓有关的参数;Nc为比例系数。
Korcak经验法则最早由地理学家Korcak在研究岛屿分布时提出,但限于当时的测试水平,只有3组岛屿被用做研究,而且关系式中的指数B被认为恒等于1/2。文献[11]指出,参数B是一个和岛屿所在海岸线的轮廓有关的参数,B=Dc/2,Dc是海岸线的分形维数。如果转化为适用于粗糙表面的关系式,则Dc=D-1,D为粗糙表面的分形维数。因此,对于二维粗糙表面B的范围为[0,1/2],而对于三维表面,B的范围为[1/2,1]。在M-B模型中,则认为B=D/2。从Korcak法则被提出以来,就不停有学者试图验证这种关系,文献[7]试图通过实验的方法验证Korcak法则,并用来预测粗糙表面微凸体的整体分布。尽管实验确实证明了接触点尺寸和个数符合指数关系,但并没有证明指数B和分形维数D的关系。文献[12]没有通过验证,而是直接利用Korcak法则计算粗糙表面的分形维数。至今为止,Korcak法则尽管被多次使用,但尚未被人明确证明是否普遍适用于任何分形表面,或者是否适用于粗糙表面上微凸体尺寸分布的研究。因此,本文将通过大量的数值实验验证Korcak法则及其在粗糙表面研究中的适用性。
1.1.1 模拟分形表面的点数对模拟结果的影响 本文选用分形维数D=1.2的粗糙表面测试数值模拟结果,模拟点数独立性如图1所示。之所以要做模拟点数独立性测试,是因为当模拟点数达不到一定数量时,分形表面就不会表现出自仿射性。换言之,当利用电脑软件模拟一个确定轮廓时,如果使用的点数不够,也就是分辨率太低的话,经过多次放大后的轮廓,不会跟原来的相似。因此,在对Korcak法则进行验证之前,有必要先研究用于分形表面模拟的点数对模拟结果的影响。

图1 模拟点数对结果的影响
由图1发现,随着模拟点数的增加,模拟结果逐渐趋于稳定,当点数超过70 000后,数值模拟结果基本可以认为跟模拟点数的选取无关。因此,本文选取最优化点数为70 000来模拟粗糙表面轮廓,图1中的纵坐标指数x将会在后面进一步讨论。
1.1.2 Korcak海岛实验数值仿真 本文利用数值仿真的方法验证Korcak测试海岛分布的实验。首先,用经典的W-M函数生成海底轮廓,而海平面则用一个绝对平面代替,如图2所示。从图2可以看到,复杂的海底轮廓被海平面截断,而截断的面积就是海岛的面积。

图2 Korcak实验示意图
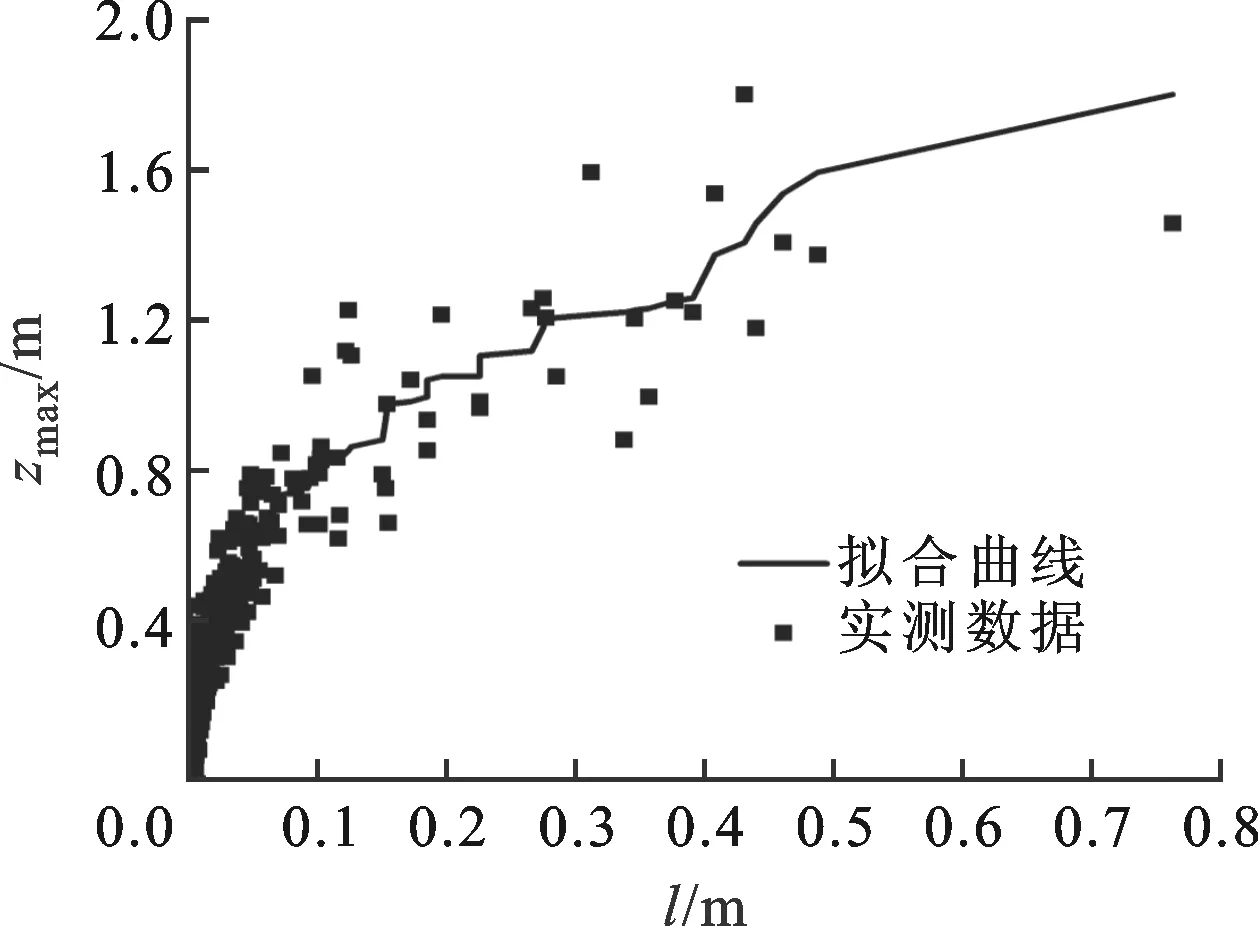
如同Korcak在实验中所做的,本文利用软件对一定取样长度内的岛屿个数N及岛屿直径l进行了记录,即所有被海平面截断的海底轮廓的长度和个数,结果表明:大于某一确定直径的岛屿的个数随此直径的增大而减小,其在双对数坐标下的关系如图3所示。

图3 岛屿个数N与岛屿直径l的关系
从图3可以看出,岛屿个数N与岛屿直径l满足指数关系,即
N(L>l)=Ncllx
(2)
式中:Ncl为比例系数。
为了研究指数x与海底轮廓的分形维数D的关系,本文分别选取从1.2到1.8的7组不同分形维数的海底轮廓进行Korcak海岛实验,从而得到了指数x和分形维数D的关系如图4所示。从图4中可以看出,指数x和分形维数D的关系可表示为
x=1-D
(3)
因此式(2)可化为
N(L>l)=Ncll1-D
(4)
为了验证式(4)并非某种特定曲线的特例,除了W-M函数外,本文还选用分形布朗函数模拟分形表面(海洋轮廓),得到的结果如图4所示。两种曲线得到的结果基本无差别,从而证明式(4)所示的关系是所有分形表面的固有特性。至此,Korcak的海岛实验已经通过软件模拟的方法得到了验证。因为Korcak法则是分形曲线的固有特性,所以在验证过程中,如果将海底轮廓改为粗糙表面,亦可证明,Korcak法则同样适用于分形粗糙表面。

图4 指数x和分形维数D的关系
1.1.3 不同的海平面高度对实验结果的影响 现实中,海平面处于不停的波动状态,每次测量时,海平面高度都是随机的,因此本文做了一个有趣的数值实验以研究不同海平面高度对实验结果的影响,结果如图5所示。图中选取的海底轮廓的分形维数为1.3,对于每个海平面高度,本文都分别进行了3次Korcak海岛实验。通过图5可以观察到,海平面的轻微波动不会影响实验结果,但当海平面过高或过低(高于海岛轮廓高度的80%或低于海底轮廓高度的30%)时,实验结果可能出现较大误差。这在证明Korcak经验法则的稳定性的同时,也从另一方面证明,Korcak在不同时间内测得的岛屿个数与岛屿面积的关系无太大的差别。

图5 不同海平面高度占海底高度的比例对实验结果的影响
1.2 接触点面积与该接触点上最大变形量的关系
看上去近乎平面的粗糙表面上其实有很多大小不一的微凸体[13-14]。当两粗糙表面接触时,随着接触压力的增加,粗糙表面上接触到的微凸体会逐渐消失或者结合成为更大的微凸体,所以对微凸体的跟踪较为复杂。不同于M-B模型,本文将不再研究微凸体如何变形,而仅讨论自仿射接触点(简称接触点)的变化。接触点和微凸体的区别在于接触点是一个动态概念,在接触过程中存在,离开接触便没有意义,并且一个接触点可能由很多微凸体组合而成。因此,接触点的概念比微凸体更复杂而且更适合用于研究接触过程。利用W-M函数生成的粗糙表面上的接触点也应该是很多余弦函数叠加的结果,因为W-M函数本身就是多个余弦函数的叠加,而在M-B模型中,却利用单余弦函数模拟微凸体,这必然导致计算结果不准确。另外,使用接触点的概念也可以排除分形接触模型中的很多假设,如传统接触理论中,认为微凸体之间的相互作用可以忽略,这和实际不太相符。利用接触点的概念后,将不再需要考虑微凸体的相互作用,因为接触点本身就是微凸体相互作用的结果,如果没有相互作用,微凸体和接触点的概念将是一致的。然而,多余弦函数叠加的显示表达式并不容易获得,所以从M-B模型被提出到现在,都没有学者提出改进方案。鉴于以上原因,本文利用数值仿真实验方法,统计地研究接触点最大变形量与接触面积的关系,然后利用此关系对分形接触模型进行修正,得到更符合实际情况的分形接触理论。
粗糙表面间的接触可简化如图6所示。首先,利用W-M函数生成一个可变形的分形粗糙表面,然后使刚性平面与该粗糙表面接触,得到截断后的表面。在这个过程中,本文记录了接触点直径l与最大接触变形量zmax关系如图7a所示,对图中的点进行拟合并画在双对数坐标下如图7b所示,其中分形特征尺度G=0.12 m1/2,分形维数D=1.7。
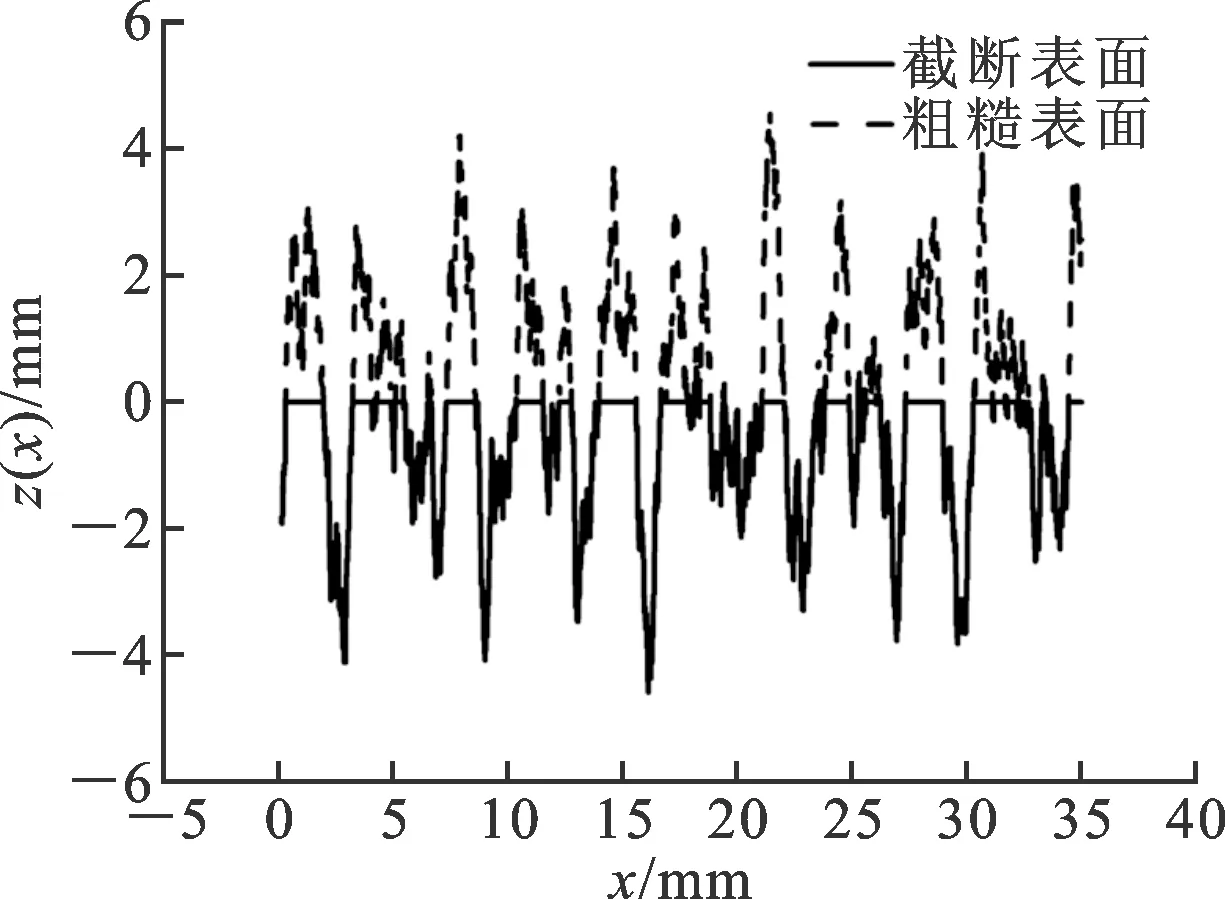
图6 两粗糙表面接触的简化示意图
(a)接触点直径l与最大变形量zmax的关系

(b)接触点直径l与最大变形量zmax关系的双对数形式图7 最大变形量与接触点直径的关系
通过图7可以发现,在双对数坐标下接触点直径和最大变形量近似满足线性关系,因此最大变形量可以假设为
zmax=Imlxm
(5)
式中:Im和xm分别为最大变形量时的乘子和指数。值得注意的是,在传统的M-B模型中,zmax-MB=GD-1l2-D,G被定义为粗糙表面的分形特征尺度,但这仅仅是利用单余弦函数模拟微凸体而得到的结果。

图8 指数xm和分形维数D的关系
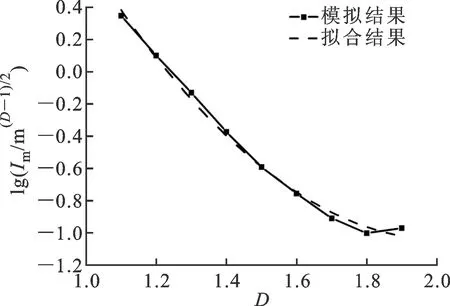
1.2.1 指数xm本文通过W-M函数模拟了不同的分形曲线,从而得到了指数xm和分形维数D的关系如图8所示。图8表明,指数xm和分形维数D近似满足线性关系,即
(6)
对于M-B模型中的微凸体,xm-MB=2-D。本文同样对不同的分形特征尺度G进行了研究,同时除了W-M函数外,分形布朗函数也被用作模拟粗糙表面轮廓。研究发现,指数xm由分形维数D唯一决定,跟其他参数无关。
1.2.2 乘子Im比起指数xm,乘子Im的确定更复杂。在不同的分形特征尺度下,乘子随分形维数的变化情况也不同,如图9所示。从图9中可以总结以下两点。
(a)G=1.2×10-3 m1/2

(b)G=1.2×10-2 m1/2

(c)G=1.2×10-1 m1/2

(d)G=1.2 m1/2图9 不同分形特征尺度G下乘子与分形维数的关系
(1)乘子Im由分形特征尺度G和分形维数D共同决定。在不同的特征尺度G下,乘子随分形维数的变化规律也不同,图9中利用多项式拟合了这一关系。
(2)随着分形特征尺度G的增加,最小乘子所对应的分形维数逐渐减小。
本文利用多项式拟合乘子与分形维数及特征尺度的关系
lgIm=3-lgG+(-4+lgG)D+1.8D2
(7)
Im=GD-1101.8D2-4D+3
(8)
而对于M-B模型,Im-MB=GD-1,两者之比为
(9)
从式(9)可以发现,随着分形维数的增加,两种方法得到的最大变形量的比值也逐渐增加,当分形维数D=1.1时,比值最小。换言之,分形维数越大,多余弦函数叠加的效果也就越显著。
为了对比单余弦函数和多余弦函数构造接触点的不同,本文选取参数G=0.12 m1/2、D=1.5来构造接触点,通过图10可以发现,单余弦函数所构造接触点的最大变形量过小。

图10 单余弦函数和多余弦函数构造接触点的对比
2 基于自仿射接触点的分形接触模型
在得到自仿射接触点的最大变形量与接触面积的关系后,本文将利用此关系进一步推导新的分形接触模型。本文推导的分形接触模型基于粗糙表面均为各向同性的无润滑表面,并且可以利用W-M函数模拟的假设。如图6所示,由于所有接触都不完美,接触表面由很多个不同尺度的接触点组成。在经典分形接触模型M-B中,微凸体概念的使用并不准确,因此在对其进行改正,得到一个全新的、更加准确的接触点定义后,本文将推导更符合粗糙表面分形特性的分形接触理论。
在利用W-M函数生成的分形表面上,接触点表现为由多个余弦函数叠加而成,如图11所示。

图11 分形粗糙表面接触点示意图
从图11中可以看出,单一接触点的形状与余弦函数很相似。因此,在得到接触点最大变形量与接触直径的关系后,本文假设直径为l的接触点的变形量可表示为
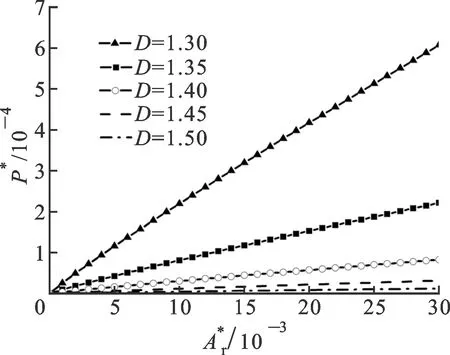
-l/2 (10) 该接触点在顶点处的曲率半径为[2] (11) 在第1节中已经证明经典的Korcak法则适用于粗糙接触表面,即 (12) 式中:al为接触点最大接触面积。因此,接触点的尺寸分布函数可由式(12)的微分得到 (13) 根据Hertz接触理论,接触点的接触面积和弹性接触压力可表示为 a=πRz (14) (15) 式中:E为复合弹性模量。 塑性接触压力为[8] pp(a)=Kσya (16) 式中:K为材料硬度系数;σy为材料屈服强度。 将式(14)和式(11)带入式(15),得到弹性接触压力和接触面积的关系为 (17) 由于受力的不同,粗糙表面的接触点将表现为弹性变形或塑性变形的状态,而弹性变形与塑性变形的临界变形量为[2] (18) 利用本文得到的接触点的最大变形量与接触面积的关系,可得接触点的临界接触面积为 (19) 式中:φ=σy/E。 正如传统分形接触理论M-B模型中发现的一样,本文接触点的变形规律同样为:当接触点的接触面积大于临界接触面积时,接触点处于弹性接触阶段;当接触面积小于临界接触面积时,接触点处于塑性接触阶段。这一特点与传统的认识相悖,也有学者一直在争论称其不合理,因此本文将结合分形表面的特点论述这一规律。 对于分形表面上任意一个接触点,不论接触面积大小,其最大接触变形量与接触直径满足式(5),因此最大接触变形量与接触直径的比值为ζ=zmax/l=Iml(1-D)/2。由于分形维数1 将式(13)带入单个接触点的接触压力表达式,即可得到整个接触面上的弹性和塑性接触压力 对于不同材料及尺寸的粗糙表面,将总压力转换为非量纲形式将更有利于对比研究 3.1 与M-B模型及G-W模型对比 为了验证推导得到的接触模型,将本文模型与经典的M-B和G-W模型进行对比,如图12所示。其中比较关心的参数有D=1.38,G*=10-10,Aa=10-6m2及φ=0.05[8]。 图12 3种模型结果对比 通过图12可以看出,由于G-W模型是一个弹性模型,较少考虑塑性接触,因此G-W模型在整体上会低估粗糙表面的接触压力,M-B模型则利用W-M函数中的单个余弦函数模拟微凸体。本文的研究表明,自仿射接触点比微凸体更适合应用于分形接触模型的推导中,在接触中,单个余弦函数模拟微凸体所得到的最大接触变形量偏小。另外,M-B模型中微凸体尺寸分布函数的使用也不准确。综上所述,M-B模型高估了接触压力。因此,图12说明本文推导的模型能更加准确地揭示接触机理。 3.2 分形维数及分形特征尺度对结果的影响 在分形接触模型中,粗糙表面的分形维数和特征尺度由接触表面的材料决定,因此有必要研究分形维数及特征尺度对分形模型模拟结果的影响。本文选取了不同的分形维数对比理论推导,结果如图13所示。在相同的接触面积下,分形维数越大的表面,接触压力越小。究其原因,分形维数和接触点的分布有直接关系:在一定的面积内,接触点越多,粗糙面的分形维数越大。因此,分形维数越小的表面,就需要越大的力以使粗糙表面发生相同的变形,从而具有相同的接触面积。 图13 分形维数对接触模型的影响 本文选取不同的分形特征尺度对比理论推导,结果如图14所示。结果与预想的一样,为了达到相同的接触面积,具有较大分形特征尺度的表面需要的变形量更大,因此压力也必须足够大。 图14 分形特征尺度对接触模型的影响 (1)利用数值实验方法,通过选用不同的分形曲线验证了分形研究中广泛使用的Korcak法则,同时研究了不同的海岸线高度对实验结果的影响,从而证明Korcak法则是分形曲线的固有特性。 (2)研究了分形粗糙表面的接触机理,发现在传统的分形接触理论中,微凸体概念的使用并不恰当,因此利用自仿射接触点代替微凸体进行理论推导。 (3)得到了接触点变形量和接触点面积的关系。随后,利用赫兹接触理论,计算了产生该变形量所需的接触压力,结合接触点的尺寸分布函数得到了整个粗糙表面的压力分布,从而推导了新的接触模型。研究表明,不同的分形维数和分形特征尺度对接触模型的影响较大。 [1]GORYACHEVA I G.Contact mechanics in tribology [M].Berlin, Germany: Springer-Verlag, 1998: 1-3. [2]GREENWOOD J A, WILLIAMSON J B P.Contact of nominally flat surfaces [J].Proceedings of the Royal Society of London: Series A Mathematical and Physical Sciences, 1966, 295(1442): 300-319. [3]CHANG W R, ETSION I, BOGY D B.An elastic-plastic model for the contact of rough surfaces [J].Journal of Tribology, 1987, 109(2): 257-263. [4]ZHAO Y W, MAIETTA D M, CHANG L.An asperity microcontact model incorporating the transition from elastic deformation to fully plastic flow [J].Journal of Tribology, 2000, 122(1): 86-93. [5]YOU J M, CHEN T N.Statistical model for normal and tangential contact parameters of rough surfaces [J].Proceedings of the Institution of Mechanical Engineers: Part C Journal of Mechanical Engineering Science, 2011, 225(1): 171-185. [6]MAJUMDAR A.Fractal surfaces and their applications to surface phenomena [D].Berkeley, USA: University of California, 1989. [7]MAJUMDAR A, BHUSHAN B.Role of fractal geometry in roughness characterization and contact mechanics of surfaces [J].Journal of Tribology, 1990, 112(2): 205-216. [8]MAJUMDAR A, BHUSHAN B.Fractal model of elastic-plastic contact between rough surfaces [J].Journal of Tribology, 1991, 113(1): 1-11. [9]MORAG Y, ETSION I.Resolving the contradiction of asperities plastic to elastic mode transition in current contact models of fractal rough surfaces [J].Wear, 2007, 262(5): 624-629. [10]MIAO X M, HUANG X D.A complete contact model of a fractal rough surface [J].Wear, 2014, 309(1): 146-151. [11]MANDELBROT B B.The fractal geometry of nature [M].London, UK: MacMillan, 1983: 116-119. [12]RUSS J.Fractal surfaces [M].New York, USA: Springer-Verlag, 1994: 14-16. [13]张学良, 黄玉美.机械结合部动态特性参数识别的优化方法 [J].太原重型机械学院学报, 1995, 16(4): 314-318. ZHANG Xueliang, HUANG Yumei.An optimization method for identification of machine joint structural parameters [J].Journal of Taiyuan Heavy Machinery Institute, 1995, 16(4): 314-318. [14]尤晋闽, 陈天宁.结合面法向动态参数的分形模型 [J].西安交通大学学报, 2009, 43(9): 91-94. YOU Jinmin, CHEN Tianning.Fractal model for normal dynamic parameters of joint surfaces [J].Journal of Xi’an Jiaotong University, 2009, 43(9): 91-94. [本刊相关文献链接] 方江龙,王小鹏,陈天宁,等.动理论在预测非阻塞性颗粒阻尼能量耗散中的应用.2015,49(4):12-17.[doi:10.7652/xjtuxb201504003] 田红亮,赵美云,郑金华,等.新的柔性结合部法向接触刚度和接触阻尼方程.2015,49(1):118-126.[doi:10.7652/xjtuxb201501020] 田红亮,陈从平,方子帆,等.应用改进分形几何理论的结合部切向刚度模型.2014,48(7):46-52.[doi:10.7652/xjtuxb 201407009] 李昕,张娟,李全福,等.面向集成电路的大尺寸单晶石墨烯的可控制备方法.2014,48(6):103-109.[doi:10.7652/xjtuxb201406018] 张超,陈天宁,王小鹏,等.颗粒阻尼线性离散元模型参数的选取方法.2014,48(3):96-101.[doi:10.7652/xjtuxb201403 018] 舒歌群,赵文龙,梁兴雨,等.约束阻尼结构的振动分析及结构参数优化研究.2014,48(3):108-114.[doi:10.7652/xjtuxb201403020] 欧阳武,陈润霖,彭林,等.考虑局部固体接触的滑动轴承主刚度和主阻尼研究[J].2014,48(1):112-117.[doi:10.7652/xjtuxb201401019] 刘石,仲继泽,冯永新,等.使用磁流变阻尼器的大型汽轮发电机定子端部绕组振动控制.2013,47(4):39-43.[doi:10.7652/xjtuxb201304008] 宿月文,陈渭,朱爱斌,等.分形特征表面接触磨损模拟.2013,47(7):52-56.[doi:10.7652/xjtuxb201307010] 薛士明,曹军义,林京,等.分数阶阻尼裂纹转子的非线性动力学特性分析.2012,46(1):76-80.[doi:10.7652/xjtuxb 201201014] 田红亮,赵春华,朱大林,等.整个螺栓结合部的法向连接动刚度及试验验证.2012,46(9):31-36.[doi:10.7652/xjtuxb 201209007] 张学良,温淑花,兰国生,等.平面结合面切向接触阻尼分形模型及其仿真.2011,45(5):74-77.[doi:10.7652/xjtuxb 201105014] 王建伟,徐晖,马宁.内嵌自主移动钢球欧拉梁自适应碰撞减振研究.2010,44(11):103-108.[doi:10.7652/xjtuxb201011 021] 刘雅琳,徐自力,上官博,等.时频域交互法在微滑移干摩擦阻尼叶片振动分析中的应用.2009,43(11):22-26.[doi:10.7652/xjtuxb200911005] 尤晋闽,陈天宁.结合面法向动态参数的分形模型.2009,43(9):91-94.[doi:10.7652/xjtuxb200909020] 曹军义,谢航,蒋庄德.分数阶阻尼Duffing系统的非线性动力学特性.2009,43(3):50-54.[doi:10.7652/xjtuxb200903 011] (编辑 杜秀杰) Self-Affine Contact Spot with Applications in Fractal Contact Theory ZHOU An’an, CHEN Tianning, WANG Xiaopeng, XI Yanhui (School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China) The numerical simulation for contact essence between fractal rough surfaces is conducted, and a concept of self-affine contact spot is introduced to propose a new fractal contact model.Compared with the asperity in classical fractal contact model, the self-affine contact spot better describes the process of fractal contact.The self-affine contact spot now gets fractal, and the assumption of no interaction between asperities is unnecessary.Under the assumption that the rough surfaces are all unlubricated isotropic surfaces, this model can be simulated by W-M function.Making use of the relationship between the maximum deformation and contact area of contact spot, the classical fractal contact model is modified to further approach the engineering practice.It is found that G-W model ignores plastic deformation of contact spot thus to underestimate the contact load of rough surfaces; M-B model leads to a smaller maximum deformation to difficultly use size-distribution function and overestimates the contact load.The self-affine contact spot instead of asperity enables to accurately evaluate the contact pressure, The more the fractal dimension (or the less the fractal characteristic scale), the less the contact pressure is needed for same contact area. contact theory; numerical simulation; fractal; asperity 2014-09-28。 作者简介:周安安(1987—),男,博士生;陈天宁(通信作者),男,教授,博士生导师。 基金项目:国家科技重大专项资金资助项目(2011ZX04002-031);陕西省科学技术研究发展计划资助项目(2014SJ-09)。 时间:2015-03-23 http:∥www.cnki.net/kcms/detail/61.1069.T.20150323.1713.004.html 10.7652/xjtuxb201506002 TH113.1 A 0253-987X(2015)06-0008-083 模型对比结果与讨论


4 结 论
