Halin图谱半径的进一步论述

张超权， 刘晓辉

(桂林航天工业学院 理学部 广西 桂林 541004)



Halin图谱半径的进一步论述

张超权， 刘晓辉

(桂林航天工业学院 理学部 广西 桂林 541004)

Halin图； 谱半径； 正则图； 行和； 内点； 外点

0 引言

矩阵谱半径的计算和估计，不仅在理论数学方面相当重要，而且在需要用到谱半径的一个初始估计值的迭代过程方面也体现出了相当重要的作用，该问题引起了大量学者的兴趣，也得到了很多重要的结果[1-4].

1969年，Halin[4]在讨论最小3-连通平面图时引入了Halin图，随后，研究者对Halin图的点、边着色、全色数、谱半径的上界和极图等展开了研究[4-8]，并得到了比较好的结果.

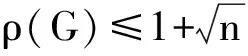
本文研究了上面不等式取得等号的极图，并且对含有2个内点的Halin图的谱半径进行了讨论，得到了该类Halin图的谱半径呈递增的趋势.

1 主要结论

设G是n阶简单连通图，A(G)是图G的邻接矩阵，A(G)的最大特征值ρ称为图G的谱半径，记为ρ(G).ρ(G)所对应的的单位特征向量X称为图G的Perron向量.G中与顶点v相关联的边的数目称为顶点v的度，如果G的所有顶点都有相同的顶点度k，则称G是k-正则图，简称为正则的.

设T是一个除1度点外，其余点的度至少是3的树，将树T的1度点顺次连接成一个圈所得到的图称为Halin图.我们称圈上的点为Halin图的外点，其余的点为Halin图的内点.

定理1 设Gn为n阶Halin图，a表示Halin图的内点个数(a≥2)，则

当a=2时，见图1，有

sv1(A2-2A)=sv1(A2)-2sv1(A)=3n1+n2+1-2(n1+1)=n1+n2-1=n-3,

sv2(A2-2A)=sv2(A2)-2sv2(A)=3n2+n1+1-2(n2+1)=n2+n1-1=n-3,

在与v1相邻的左边的n1个点中任取一个点，记为v，则

sv(A2-2A)=sv(A2)-2sv(A)=2×3+n1+1-2×3=n1+1，

在与v2相邻的右边的n2个点中任取一个点，我们不妨也记为v，则

sv(A2-2A)=sv(A2)-2sv(A)=2×3+n2+1-2×3=n2+1，

当a=3时，见图2(注：与顶点v2相邻的顶点也可能会位于下面的边上，但这并不会影响到下面行和的计算，所以我们可以假设它们全部都位于某一条边上，下面当a取别的数值时也做同样的处理)，有

图1 内点为2的n阶Halin图Fig.1 n-order Halin graphs with interior points for 2

图2 内点为3的n阶Halin图Fig.2 n-order Halin graphs with interior points for 3sv1(A2-2A)=sv1(A2)-2sv1(A)=3n1+n2+2-2(n1+1)=n1+n2,sv2(A2-2A)=sv2(A2)-2sv2(A)=3n2+n1+1+n3+1-2(n2+2)=n1+n2+n3-2,

sv=(A2-2A)=sv(A2)-2sv(A)=2×3+n3+1-2×3=n3+1=3，

当a=4时，见图3，有

sv1(A2-2A)=sv1(A2)-2sv1(A)=3n1+n2+2-2(n1+1)=n1+n2，

sv2(A2-2A)=sv2(A2)-2sv2(A)=3n2+n1+1+n3+2-2(n2+2)=n1+n2+n3-1，

sv3(A2-2A)=sv3(A2)-2sv3(A)=3n3+n2+2+n4+1-2(n3+2)=n2+n3+n4-1，

sv4(A2-2A)=sv4(A2)-2sv4(A)=3n4+n3+2-2(n4+1)=n3+n4，

sv(A2-2A)=sv(A2)-2sv(A)=2×3+n3+2-2×3=n3+2=3，

图3 内点为4的n阶Halin图Fig.3 n-order Halin graphs with interior points for 4

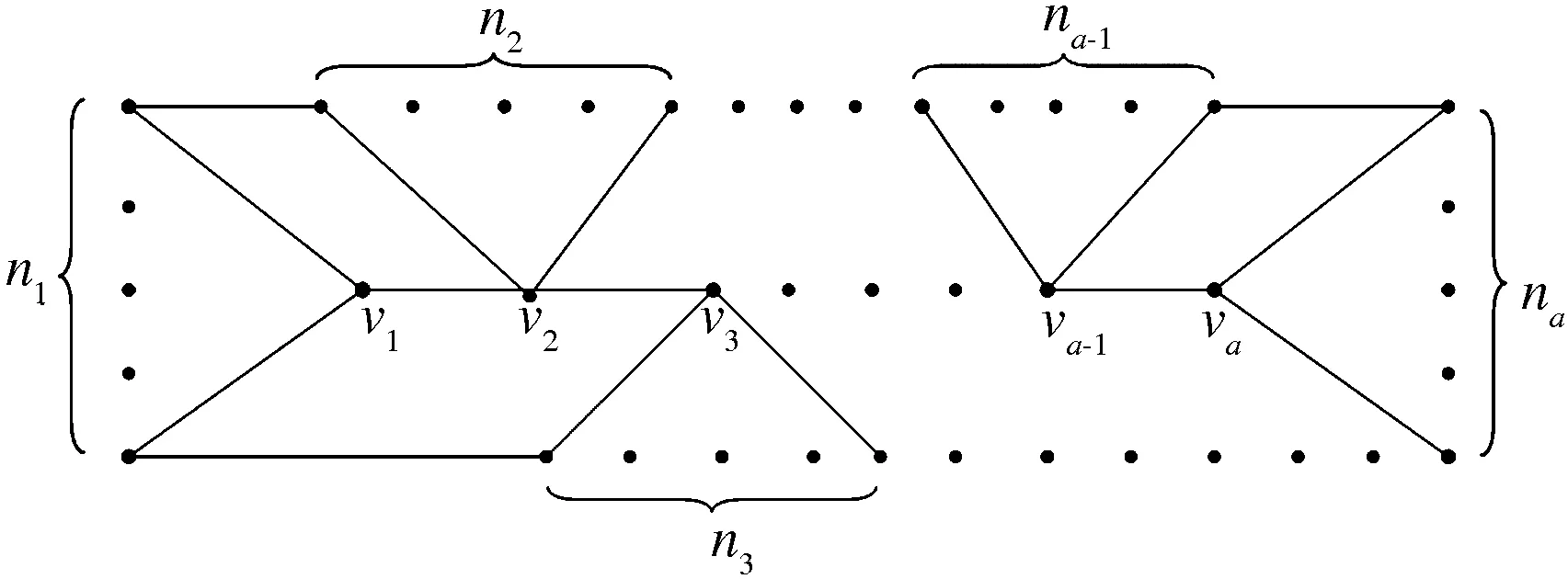
图4 内点数≥5的n阶Halin图Fig.4 n-order Halin graphs with interior points ≥5

当a≥5时，见图4，有

sv1(A2-2A)=sv1(A2)-2sv1(A)=3n1+n2+2-2(n1+1)=n1+n2,

sv2(A2-2A)=sv2(A2)-2sv2(A)=3n2+n1+1+n3+2-2(n2+2)=n1+n2+n3-1,

sv3(A2-2A)=sv3(A2)-2sv3(A)=3n3+n2+2+n4+2-2(n3+2)=n2+n3+n4,

sv4(A2-2A)=sv4(A2)-2sv4(A)=3n4+n3+2+n5+2-2(n4+2)=n3+n4+n5,

… … …

sva-2(A2-2A)=sva-2(A2)-2sva-2(A)==na-3+na-2+na-1,

sva-1(A2-2A)=sva-1(A2)-2sva-1(A)==na-2+na-1+na-1,

sva(A2-2A)=sva(A2)-2sva(A)==na-1+na,

图5 内点数为2且n1=2的n阶 Halin图(n≥7)Fig.5 n-order Halin graphs with interior points for 2 and n1=2(n≥7)

定理2 设Gn为内点数为2且n1=2的n阶Halin图(n≥7)，见图5，则

ρ(Gn-1)<ρ(Gn)<ρ(Gn+1).

证明 含有2个内点的Halin图阶数至少必须是6，所以在这里我们假设n≥7.下面证明ρ(Gn-1)严格单调递增.

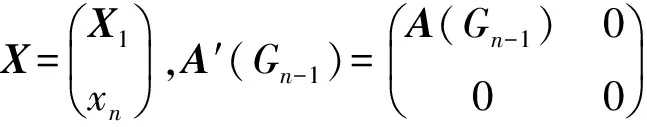
即A′(Gn-1)表示在矩阵A(Gn-1)的基础上加一行和一列0所得到的n阶矩阵.则

XTA(Gn)X-XTA′(Gn)X=XT(A(Gn)-A′(Gn))X=2(x2xn+x4xn+xn-1xn-x4xn-1)=

2[(x2+x4+xn-1)xn-x4xn-1],

2 数值实例

我们通过Mathematics演算得到了内点数为2且n1=2的部分n阶Halin图Gn的谱半径，见表1.

表1 内点数为2且n1=2的n阶Halin图的谱半径Tab.1 The spectral radius of n-order Halin graphs with interior points for 2 and n1=2

上面表格中的结果显示随着n取值的增大ρ(Gn)呈递增的趋势.

3 结束语

[1] Liu Jianzhou，Zhang Chaoquan．Some criteria for nonsingular H-matrices[J]． Natural Science Journal of Xiangtan University，2008，30(3)：21-29．

[2] 张超权，刘晓辉．矩阵谱半径的一类迭代算法[J]．梧州学院学报，2009，19(6)：16-18．

[3] 徐允庆．关于图谱半径的一个不等式[J]．信阳师范学院学报:自然科学版，1992，5(3)：263-268．

[4] Halin R. Studies on minimallyn-connected graph[C]∥Proceedings of Combi Math and its Applications. Oxford，1969．

[5] 李鸿祥，张忠辅，张建勋．Halin图的色性[J]．上海铁道学院学报，1994,15(1):19-24．

[6] Zhang Zhongfu，Wang Jiangfang， Li Hongxiang．A note on the total chromatic number of 3-regular Halin graph[J]．Mathematics in Economics，1997,14(2):9-12．

[7] 束金龙，洪渊．外平面图和Halin图谱半径的上界[J]．数学年刊，2000,21A(6)：677-682．

[8] 袁劲松，束金龙．Halin图谱半径的新上界及极图[J]．高校应用数学学报，2008,23(3):335-342．

(责任编辑：王浩毅)

A Further Discussion of the Spectral Radius of Halin Graphs

ZHANG Chao-quan， LIU Xiao-hui

(FacultyofScience,GuilinUniversityofAerospaceTechnology,Guilin541004，China)

Halingraph;spectralradius;rowssum;interiorpoint;exteriorpoint

2015-01-10

广西壮族自治区教育厅科研项目，编号201106LX709;桂林航天工业学院2012年科研项目，编号X12Z022.

张超权(1979-)，女，湖南桃江人，讲师，硕士，主要从事应用数学研究，E-mail：zhang_chao3201@163.com.

张超权，刘晓辉.Halin图谱半径的进一步论述[J].郑州大学学报：理学版，2015，47(3)：30-33.

O

A

10.3969/j.issn.1671-6841.2015.03.005