具有多重休假和修复非新的Gaver并联系统
2015-12-27孟宪云陈雨田
金 宇, 孟宪云, 张 力, 陈雨田
(燕山大学 理学院 河北 秦皇岛 066004)
具有多重休假和修复非新的Gaver并联系统
金 宇, 孟宪云, 张 力, 陈雨田
(燕山大学 理学院 河北 秦皇岛 066004)
研究了一个修理工多重休假、两个修复如新同型部件并联和一个修复非新部件冷贮备的Gaver并联系统. 修理工可多重休假, 休假时间服从一般连续型分布. 运用几何过程理论、补充变量法和Laplace变换等数学工具, 得到系统瞬时可用度、瞬时可靠度等可靠性指标.
多重休假; 修复非新; 补充变量; 可用度
0 引言
Gaver并联可修系统在可修系统的研究中受到很多关注. 因为设备都有一定的使用寿命, 修复非新这一假定也越来越多地应用到可修系统的研究中, 使理论更接近实际情况. 文献[1]在假定部件修复如新的前提下研究了带有一个冷贮备部件的Gaver并联可修系统,利用向量Markov过程理论和Laplace变换方法, 通过求解一组微分方程, 得到了系统稳态可用度和稳态故障频度等可靠性指标. 文献[2]研究了两个修复非新且不同型部件的冷贮备退化可修系统,并假定随着修理次数的增多, 每次修理时间越来越长, 工作时间越来越短;系统中只有一个单重休假的修理工,利用微分方程和Laplace变换等方法得到一系列可靠性指标. 文献[3-5]分别从并联、冷贮备和相依等角度研究分析了两部件可修系统. 文献[6-8]专注于不同分布的冷贮备可修系统,研究分析了带有修复非新的两个不同型部件的冷贮备退化可修系统. 文献[9-10]分别研究了不同的温贮备系统. 文献[11-12]分别研究了一般分布的可修系统和可修系统在计算机方面的应用.
作者在已有文献的基础上, 将修复非新这一假定引入到Gaver并联可修系统中. 假定系统中两个并联部件修复如新, 工作时间服从指数分布, 修理时间服从一般分布. 一个冷贮备部件修复非新, 且随着修理次数的增多, 寿命越来越短, 修理时间越来越长,运用补充变量法和Laplace变换得到系统的可用度、可靠度等可靠性指标.
1 模型假定
(1)系统由两个同型部件、一个不同型部件和一个修理工组成.
(2)初始时刻三个部件都是新的, 两个同型部件工作, 一个不同型部件冷贮备, 修理工休假.
(3)部件状态之间的转换通过转换开关实现, 开关完全可靠且在瞬间完成.
(4)对两个同型部件的修理是修复如新, 一个不同型部件的修理是修复非新的.
(5)系统的第n个周期是指不同型部件的第n-1次修理完成与第n次修理完成之间的时间间隔,n=1,2,3,…



X(2)和Y(2)分别记为两个同型修复如新部件的工作寿命和修理时间,其分布为
F(2)(t)=1-exp(-λ2t),

修理工的休假时间服从一般分布

其中,t≥0,a>0,λ1>0,λ2>0,α>0,μ1>0,μ2>0;n=1,2,…
(7)修理工多重休假, 无空闲. 若一次休假结束后无故障部件, 则再次休假. 若休假结束后有两个或两个以上部件故障, 随机选一个故障部件进行修理. 所有故障部件修复后, 修理工又马上开始休假.
(8)所有随机变量均相互独立.
2 模型分析
记N(t)为系统在t时刻所处的状态, 则系统状态如下:
0: 两个如新部件工作, 非新部件贮备, 修理工休假;
0′: 一个如新部件和非新部件工作, 另一个如新部件贮备, 修理工休假;
1: 一个如新部件和非新部件工作, 另一个如新部件故障, 修理工休假;
1′:两个如新部件工作, 一个非新部件故障, 修理工休假;
2: 一个如新部件工作, 非新部件和另一个如新部件故障, 修理工休假;
2′: 非新部件工作, 两个如新部件故障, 修理工休假;
3: 一个如新部件和非新部件工作, 另一个如新部件修理;
3′:两个如新部件工作, 非新部件修理;
4: 一个如新部件工作, 另一个如新部件修理, 非新部件待修;
4′: 一个如新部件工作, 非新部件修理, 另一个如新部件待修;
4″: 非新部件工作, 一个如新部件修理, 另一个如新部件待修;
5: 三个部件均待修, 修理工休假;
6: 一个如新部件修理, 另一个如新部件和非新部件待修;
6′: 非新部件修理, 两个如新部件待修.
上述状态中, 状态0,0′,1,1′,2,2′,3,3′,4,4′,4″是系统的工作状态, 状态5,6,6′是系统的故障状态. 由假定知此过程不是Markov过程, 引入补充变量如下:
X(t): 当N(t)=0,0′,1,1′,2,2′,3,3′,4,4′,4″时,X(t)表示在时刻t修理工已经用去的休假时间;
Y(t): 当N(t)=5,6,6′时,Y(t)表示在时刻t部件已经用去的修理时间;
S(t): 非新部件在时刻t的周期数.
则{S(t),N(t),X(t),Y(t),t≥0}构成一个Markov过程.有
Pik(t,x)=P{N(t)=i,S(t)=k,x≤X(t) Pjk(t,y)=P{N(t)=j,S(t)=k,y≤Y(t) 引入如下记号: 引理1 系统状态方程组解的Laplace变换表达式为 (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) ak-1λ1(ak-1λ1-3λ2)(ak-1λ1-2λ2)-1(e-ak-1λ1x-1)-2λ2(e-(ak-1λ1+λ2)x-1)](ak-1λ1-λ2)-1× (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) 其中, c5k(s)=(ak-1λ1-λ2)-1[λ2h*(s+ak-1λ1+λ2)- ak-1λ1h*(s+2λ2)+(ak-1λ1-λ2)h*(s+2λ2)], 证明 根据模型假定及系统分析可建立系统状态方程组如下 : (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) 边界条件如下: (37) (38) (39) (40) (41) (42) (43) (44) (45) Pik(t,0)=0,i=1,1′,2,2′,5, (46) (47) (48) (49) 初始条件为P01(0,1)=0, 其余为零. 定理1 设系统瞬时可用度为A(t), 则其Laplace变换表达式为 证明 系统瞬时可用度指在时刻t系统处于工作状态的概率, 本模型中工作状态有0,0′,1,1′,2,2′,3,3′,4,4′,4″,则有 两边做Laplace变换,有 定理2 设系统瞬时故障频度为W(t), 则其Laplace变换表达式为 证明 系统瞬时故障频度是指在时刻t系统由工作状态转为故障状态的概率,在本模型中即指系统中只有一个部件工作, 且该工作部件故障的概率. 则有 定理3 设系统瞬时等待修理的概率为Pw(t), 即系统处于故障状态的同时修理工处于休假状态的概率,亦即本模型的状态5, 则有 证明 两边做Laplace变换, 并将引理1的相关结果代入,即得 定理4 设修理工的休假概率为Pv(t), 则其Laplace变换表达式为 其中,K13=[(ak-1λ1-λ2)(ak-1λ1-2λ2)]-1,K14=[2(λ2-ak-1λ1)(ak-1λ1+λ2)]-1. 证明 分析系统状态可知修理工休假的状态有0,0′,1,1′,2,2′,5,则 定理5 设系统可靠度为R(t),则其Laplace变换表达式为 证明 由可靠度定义可得 (50) 为求得系统的可靠度R(t), 将本模型中的故障状态5,6,6′视为随机过程的吸收态, 得到一个新的随机过程,此时系统状态空间为 E={0,0′,1,1′,2,2′,3,3′,4,4′,4″}. 系统方程与前系统大致相同, 不同之处在于删掉方程(34)~(36),(44)和(45), 另由方程(41)、(42)得 (51) 由方程(43)得 (52) 对式(50)做Laplace变换可得 利用引理1的相关结果以及方程(51)、(52)可得 (53) (54) (55) (56) 在实际情况中, 系统部件往往不是修复如新的, 随着部件使用时间越久, 修复次数增多,部件修理时间会越来越长,鉴于此,将修复非新这一条件加入到Gaver并联可修系统中,研究了修理工可多重休假,并带有一个修复非新的冷贮备部件的Gaver并联可修系统,利用Markov过程理论和Laplace变换的方法,得到了系统瞬时可靠度的Laplace变换式,以及系统瞬时可用度等一系列可靠性指标. [1] 岳德权, 朱建玲, 秦雅玲, 等.修理工可多重休假的带有一个冷贮备部件的Gaver并联系统[J].系统工程理论与实践, 2006, 6(6):59-68. [2] 梁小林,莫兰英,唐小伟.具有修理工休假的冷贮备退化可修系统的研究[J].系统工程学报,2010,25(3):426-432. [3] 马淑莲,汪云芬, 刘海涛,等.具有单重休假和修复不如新的两部件并联系统[J].数学的实践与认识,2011,41(16):111-117. [4] 孟宪云,刘海涛,李芳,等.两个不同型部件冷贮备系统的几何过程模型[J].辽宁工程技术大学学报:自然科学版,2011,30(1):146-149. [5] 刘海涛,孟宪云,张建龙.两个相依部件并联系统的几何过程模型[J].黑龙江大学自然科学学报,2012,29(2):169-173. [6] Chen Yutian,Meng Xianyun,Chen Shengqiang. Reliability analysis of a cold standby system with imperfect repair and under Poisson shocks[J].Mathematical Problems in Engineering,2014,4:1-11. [7] 赵丹,周岩,孟宪云,等.寿命服从PH分布的冷贮备可修系统[J].河南科技大学学报:自然科学版, 2014,35(1):92-97. [8] Yu Haiyang,Yalaoui F,Chtelet E, et al. Optimal design of a maintainable cold-standby system[J]. Reliability Engineering and System Safety,2007,92(1): 85-91. [9] 孟娅丽,郑海鹰.修理工可多重休假的温贮备系统[J].浙江大学学报:理学版, 2012,39(5):517-523. [10]刘海涛,孟宪云.具有单重休假和修复不如新的两部件温贮备系统[J].自动化学报, 2012,38(4):639-646. [11]Wen Zhiyuan,Gen Qixu.Modelling of a deteriorating system with repair satisfying general distribution[J]. Applied Mathematics and Computation, 2012, 218(11): 6340-6350. [12] 陶有德,于景元,朱广田. 一类可修复计算机系统的稳定性和可靠性[J].信阳师范学院学报:自然科学版, 2011,24(1):18-21. (责任编辑:孔 薇) Gaver’s Parallel System with Repair of Non-new and a Repairman with Multiple Vacations JIN Yu, MENG Xian-yun, ZHANG Li, CHEN Yu-tian (CollegeofScience,YanshanUniversity,Qinghuangdao066004,China) A Gaver’s parallel system attended by a repairman with multiple vacations, two parallel units with repair of new and a cold standby unit with repair of non-new was studied. The repairman vacation time obeyed the general distribution. The system’s instantaneous availability, instantaneous reliability and other reliability indices were obtained by using the geometric process theory, the supplementary variable method, Laplace transform and other math tools. multiple vacation; repair of non-new; supplementary variable; availability 2015-03-12 河北省教育厅高等学校自然科学研究指导项目,编号Z2014123. 金宇(1988-),女,黑龙江伊春人,硕士研究生, 主要从事可靠性理论应用研究,E-mail: 624268434@qq.com. 金宇, 孟宪云, 张力,等. 具有多重休假和修复非新的Gaver并联系统[J].郑州大学学报:理学版,2015,47(3):7-16. O213.2 A 1671-6841(2015)03-0007-10 10.3969/j.issn.1671-6841.2015.03.002

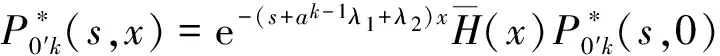


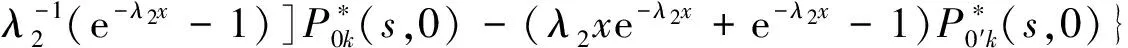



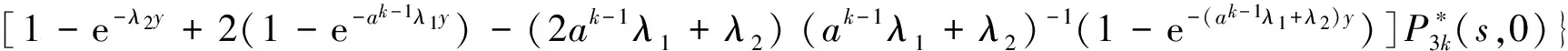



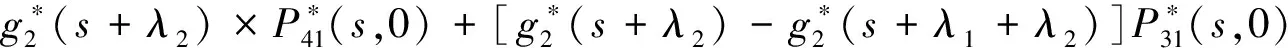


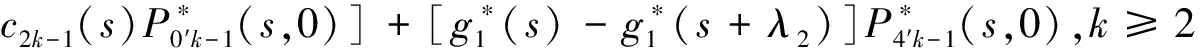
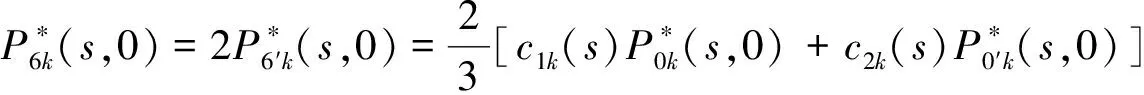

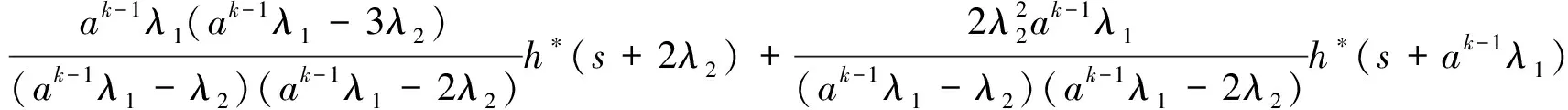
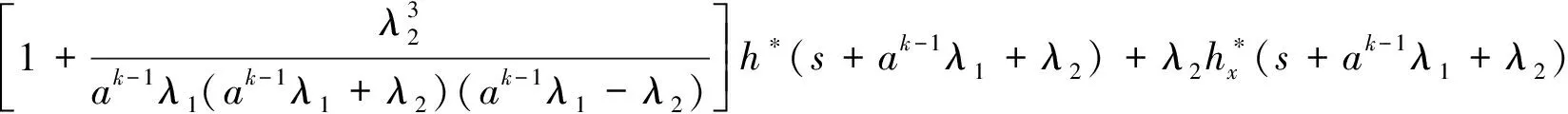

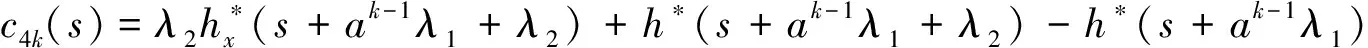

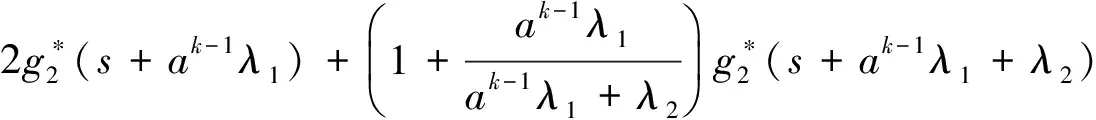
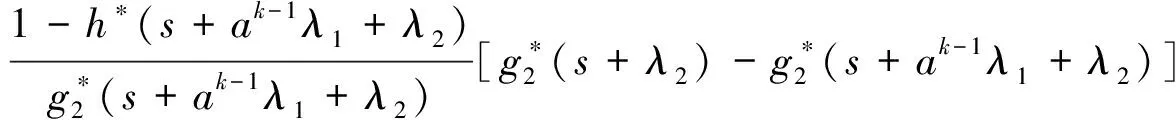

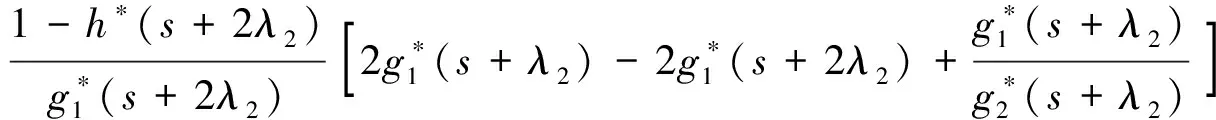




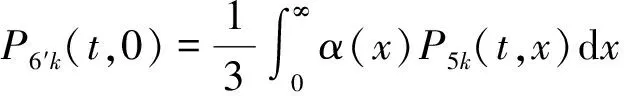
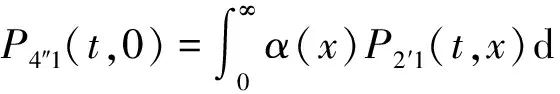
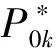
3 主要结果及证明
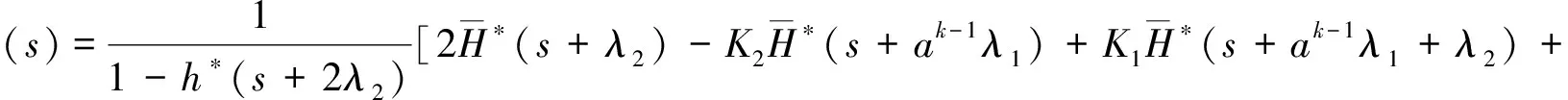


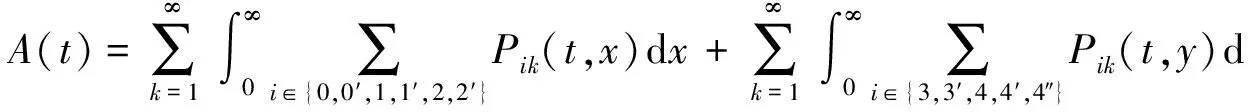

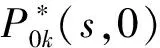


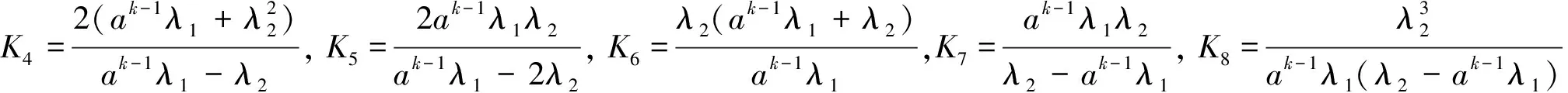

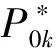

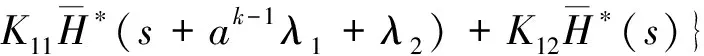


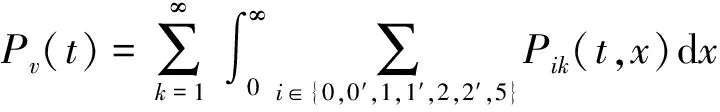




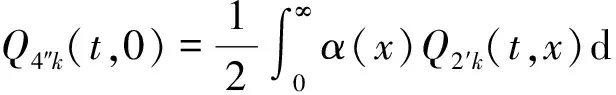

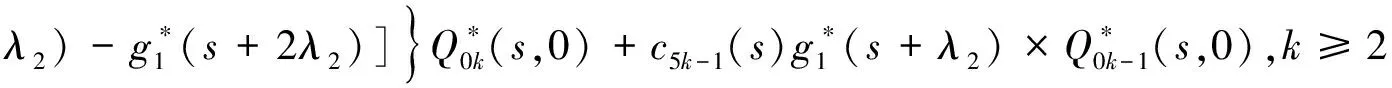


4 结束语
