完备自适应近邻图嵌入的局部鉴别投影算法*

2015-12-26王永茂

数据采集与处理 2015年6期

关键词：降维识别率人脸

王永茂李赓

(河南理工大学计算机科学与技术学院,焦作,454000)

完备自适应近邻图嵌入的局部鉴别投影算法*

王永茂李赓

(河南理工大学计算机科学与技术学院,焦作,454000)

针对基于自适应近邻图嵌入的局部鉴别投影算法(Neighborhood graph embedding based local adaptive discriminant analysis, LADP)仅仅利用局部类内离差矩阵主元空间的鉴别信息而丢失了其零空间内大量鉴别信息的不足，结合全空间的基本思想提出了完备的基于自适应近邻图嵌入的局部鉴别投影算法(Complete LADP,CLADP)。在局部类内离差矩阵的零空间内，通过最大化局部类间离差矩阵提取不规则鉴别特征，在局部类间离差矩阵的主元空间内，通过最大化局部类间离差矩阵的同时最小化局部类内离差矩阵提取规则鉴别特征，最后将不规则鉴别特征和规则鉴别特征串联形成CLADP特征。在ORL，Yale以及PIE人脸库上的人脸识别实验结果证明了CLADP的有效性。

人脸识别;自适应近邻图；局部鉴别分析；完备特征；降维

引言

在诸如人脸识别的应用领域中经常会遇到高维数据，降维是重要的预处理手段之一。降维的过程就是将高维数据投影到一个低维空间内,同时保持高维数据内在的本质特征。根据投影变换是否为线性变换，降维方法可以分为线性方法和非线性方法。主元成分分析(Principle component analysis，PCA)与线性鉴别分析(Linear discriminant analysis，LDA)[1]是两种最为经典的线性降维方法。相比于线性降维方法，非线性降维方法可以很好地处理复杂的非线性分布的数据，非线性降维方法一般分为两大类：基于流形学习的降维方法[2]和基于核空间的降维方法[3]。经典的基于流形学习的降维方法包括：等距映射、局部线性嵌入(Locally linear embedding，LLE)以及拉普拉斯映射(Laplacian eigenmap，LE)，但这些算法的最大缺陷就是不能映射新的测试样本，为此，局部Fisher鉴别分析(Local fisher discriminant analysis,LFDA)[4]、局部保形投影(Locality preserving projection，LPP)[5]以及近邻保持嵌入(Neighborhood preserving projection，简称NPE)[6]等线性的基于流形学习的降维方法相继提出。另外基于核空间的降维方法也是近年来的一个重要研究方向，传统的线性降维方法可以利用核技巧得到其相应的非线性降维方法，如核主元成分分析(Kernel PCA，KPCA)和核线性鉴别分析(Kernel LDA，KDA)等。为了更好地揭示各种降维方法之间的共同特征，Yan等和提出了统一的图嵌入框架理论[7]，在降维的过程中，需要构造两类图，一个是固有图，用于描述在降维过程需要保持的几何特性；一个是惩罚图，用于描述在降维过程中需要避免的几何特性，现存的大部分降维方法都可以用图嵌入框架来描述，其差别仅仅表现在图构造的不同。

在降维的过程中，为了保持高维数据的流形结构，往往要根据数据的近邻点来构造固有图和惩罚图，然而近邻点个数的选择对于最优的投影变换影响较大。作者在文献[8]中根据样本的分布特性以及样本间的相似度自适应计算类内和类间的近邻点，提出了基于自适应近邻图嵌入的局部鉴别分析算法(Neighborhood graph embedding based local adaptive discriminant analysis，LADP)。然而，同其他降维方法一样，LADP算法也是基于向量的降维方法，在进行降维前需要将数据转换为一维向量形式，这种转换大大增加了数据的维数，由于用于训练的数据个数有限，常常遭遇小样本问题[9]，这时局部类内离差矩阵通常为奇异矩阵。为解决这一问题，通常先利用PCA对样本进行降维，使得在PCA子空间内的局部类内离差矩阵为非奇异矩阵，这实际上仅仅利用了局部类内离差矩阵主元空间的鉴别信息而丢失了其零空间的大量鉴别信息。为了充分利用主元空间和零空间内的鉴别信息，基于全空间的特征提取算法[10-12]得到了广泛的关注。本文将全空间的思想与LADP相结合，提出了完备的LADP算法(Complete LADP,CLADP)，充分利用局部类内离差矩阵的零空间和主元空间内的鉴别信息。

1 基于自适应近邻图嵌入的局部鉴别分析算法

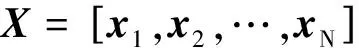
(1)

(2)

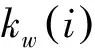
(3)

(4)

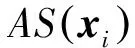
(5)

(6)

式(1)可以通过求解广义特征值问题得到

(7)

在LADP算法中，为了使SlW为非奇异矩阵，首先利用PCA方法对样本数据进行降维，使得SlW在PCA子空间内满秩，即所有的特征值均大于零，因此LADP算法仅仅利用SlW主元空间内的鉴别信息而丢失了SlW零空间内大量的鉴别信息。本文提出了CLADP算法，充分利用SlW零空间和主元空间内的鉴别信息。

2 完善的LADP算法

2.1 去除鉴别无关信息

对于总体离差矩阵SlT=SlW+SlB，其零空间由矩阵SlB和SlW的公共零空间组成，在该空间内，所有的样本均投影到同一点而无法区分，所以SlT的零空间内不含有任何鉴别信息，所有的鉴别信息存在于SlT的主元空间内。

(8)

(9)

2.2 规则鉴别特征和不规则鉴别特征提取

(10)

(1)规则鉴别特征提取

(11)

对于一个样本x，其规则鉴别特征为

(12)

式中：Ar=PQV为规则鉴别特征的投影变换矩阵。

(2)不规则鉴别特征提取

(13)

(14)

式中：Air=PQ⊥R为不规则特征的变换矩阵。

2.3 两种鉴别特征融合

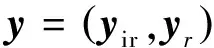
(1)自适应计算xi的类内和类间近邻点集合，根据类内类间近邻点个数构建类内类间近邻图的权值矩阵W和Wp，进而得到SlW，SlB与SlT。

3 实验结果与分析

为了评估本文提出的CLADP算法的性能，设计两类实验，实验1在ORL人脸库上，通过低维空间的可视化比较CLADP与LFDA，LADP的鉴别能力，对于CLADP算法，比较分别采用规则鉴别特征，不规则鉴别特征以及融合两种特征的识别性能；实验2在Yale和PIE人脸库上比较CLADP与PCA，LDA，LFDA与LADP等算法的分类性能。

3.1 ORL人脸库上的实验

ORL人脸库是由英国剑桥大学建立，共有40个人，每人10张图像，共有400张人脸图像，图像的面部表情和面部细节有着不同程度的变化，人脸姿势也有相当程度的变化，比较充分地反映了同一人不同人脸图像的变化和差异，ORL人脸库图像经剪切后大小均为32像素×32像素，用一个1 024维的向量表示。图1是ORL人脸库的部分样本。

图1 ORL人脸数据库Fig．1 ORL face database

3.1.1 实验1

通过对低维空间的可视化来比较CLADP与LDA，LFDA，LADP的鉴别能力。在实验中，随机从ORL人脸库中选取6个人的人脸图像，分别用符号“*”，“□”，“○”，“+”，“△”和“☆”表示，任意选择每个人的5幅图像作为训练图像，剩余的图像作为测试图像，分别采用LDA，LFDA，CLADP和LADP等算法将其投影到二维子空间内，LFDA算法中近邻点的个数k=4，LDA，LFDA与LADP算法中PCA步骤，保持99%的主元能量，图2为ORL人脸库上6人脸的二维子空间可视化结果。

图2 ORL图像库上6人脸的二维子空间Fig．2 Two dimension subspace of six persons in ORL face database

为了更加有效清晰比较各种算法的鉴别能力，采用Fisher标准值(Fisher criterion,FC)来评价在二维子空间内样本之间的区分程度[13]，FC定义如下

(15)

式中：Sw和Sb分别为二维子空间内样本类内和类间离差矩阵。FC值越大，说明在相应的子空间内的不同类别的样本的区分度越大，即鉴别能力越强。表1为在ORL人脸库的二维子空间内，各种算法的FC值。

表1 二维子空间内人脸Fisher标准值

从图2可以看出，对于ORL人脸库，在CLADP算法得到二维子空间内6个人的人脸图像具有较大的区分程度，LDA，LFDA与LADP算法得到的子空间内不同类别的人脸具有不同程度的交叠，反映在FC值上，CLADP为17.52，LADP，LFDA与LDA分别为6.66，2.47与3.91，说明在二维子空间内，CLADP的鉴别能力最强，LADP与LDA次之，LFDA最弱。

3.1.2 实验2

对于CLADP，比较分别采用规则鉴别特征，不规则鉴别特征以及融合两种特征的识别性能。实验中，随机选取每一个人的3幅图像组成训练样本集，剩余的图像组成测试样本集，重复进行10次，共得到10组不同的训练样本集和测试样本集。表2所示为分别采用规则特征，不规则特征以及融合两种特征的平均最高识别率以及对应的维数。从表2可以看出，单独采用规则鉴别特征其平均最高识别率为85.36%，单独采用不规则鉴别特征其平均最高识别率为87.69%，而融合了规则和不规则鉴别特征的CLADP算法的平均识别率进一步提高至88.19%。

表2 不同特征下LADP算法的识别率

3.2 Yale以及PIE人脸库上的实验

通过在Yale以及PIE人脸库上的实验，比较本文提出的CLADP与PCA,LDA，LFDA和LADP等算法的识别性能。Yale人脸库由美国耶鲁大学建立，包含15个人，每人11张图像，共有165张人脸图像，主要包括光照条件的变化(左侧光照、右侧光照、中央光照)，表情的变化(正常、高兴、悲伤、睡眠、惊讶、眨眼)及有无眼睛修饰等。PIE人脸图像库由68人的41 368幅不同姿态、不同光照、不同表情的图像组成。在本文中，选择了仅包括光照变化的20人的正面人脸的400张人脸图像组成的PIE子库(每人20张图像)作为实验图像。在实验中，所有图像均根据眼睛坐标进行旋转、剪切、缩放到大小为32像素×32像素的图像，未作任何其他处理。图3显示了预处理后各人脸图像库的图像示例。

图3 预处理后的图像Fig．3 Preprocessed face images

在每个库上进行实验，从每一个类别中选取m个样本组成训练样本集，记作Gm，其余的n个样本组成测试样本集，记作Pn，然后利用各种特征提取方法提取特征，最后利用欧式距离作为相似度度量的最近邻分类器完成分类任务，每组实验均重复10次。对于PCA以及LDA，LFDA，LADP中PCA步骤，实验中保持99%的能量，另外，LFDA中的近邻点个数k设置为n-1,n为训练样本集中每一个类别的个数。表3和表4分别给出了各种特征提取方法在Yale以及PIE上的平均最高识别率(括号中的数值为对应的维数)。

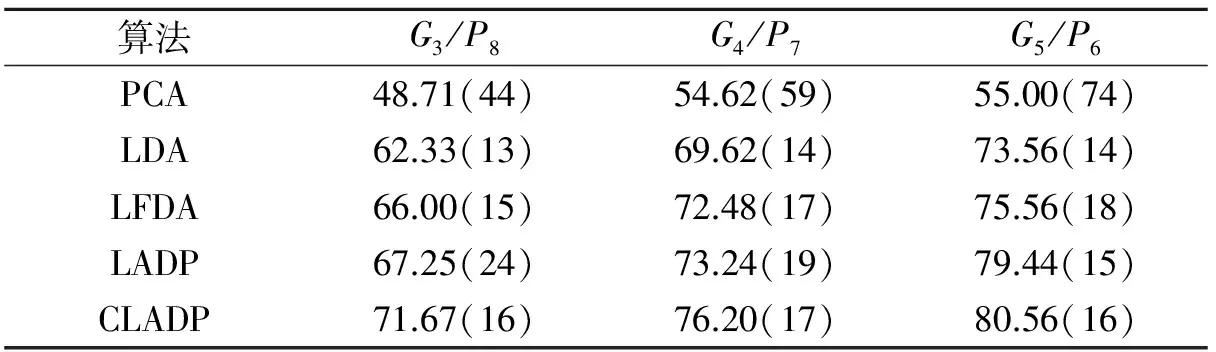
表3 Yale图像库上的平均最高识别率

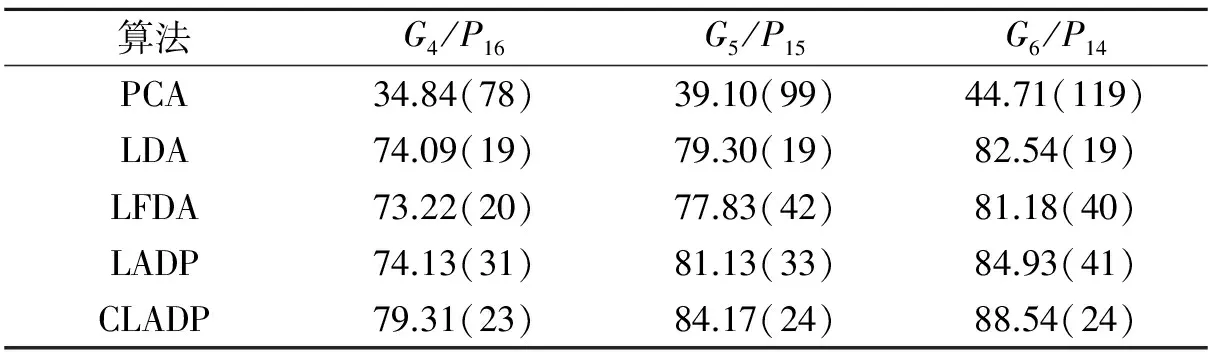
表4 PIE图像库上的平均最高识别率

从表3和表4可以看出，本文提出的CLADP算法在Yale和PIE人脸库上均取得了较好的识别效果。在Yale人脸库上，CLADP算法的识别率平均比PCA算法高23.37%，比LDA算法高7.64%，比LFDA算法高4.8%，比LADP算法高2.83%；在PIE人脸子库上，CLADP算法的识别率平均比PCA算法高44.46%，比LDA算法高5.36%，比LFDA算法高6.6%，比LADP算法高3.94%。随着训练样本的增加，CLADP与PCA，LDA，LFDA，LADP等算法的识别率都相应地提高。

4 结束语

本文在分析LADP算法仅仅利用局部类内离差矩阵主元空间内鉴别信息的不足之处的基础上，提出了同时利用主元空间和零空间内鉴别信息的CLADP算法，由于零空间的鉴别信息对于识别任务具有更加重要的作用，因此相较于LADP算法，CLADP算法具有更强的识别性能。通过人脸识别实验，本文将CLADP算法与PCA，LDA，LFDA，LADP等4种流行的降维算法进行比较，实验结果表明CLADP算法具有最好的识别率。

[1] Martinez A M, Kak A C. PCA versus LDA[J].IEEE Trans Pattern Analysis and Machine Intelligence, 2001, 23(2):228-233.

[2] 陈国明.数据降维中若干问题的研究及应用[D].广州:中山大学,2009.

Chen Guoming.Research and application of several problems in data dimensionality reduction[D].Guangzhou:Sun Yat-Sen University,2009.

[3] 林月娥.特征提取方法研究及其在人脸识别中的应用[D].哈尔滨:哈尔滨工程大学,2009.

Lin Yue′e. Research and application of feature extraction for face recognition[D].Harbin:Harbin Engineering University,2009.

[4] Sugiyama M. Dimensionality reduction of multimodal labeled data by local Fisher discriminant analysis[J].Journal of Machine Learning Research,2007,8(5):1027-1067.

[5] He X F， Niyogi P. Locality preserving projection[C]//Proceedings of the 16th Advances in Neural Information Processing Systems. Vancouver, Canada: Neural Information Processing Systems Foundation, 2003:153-160.

[6] He X F, Cai D, Yan S C, et al. Neighborhood preserving embedding [C]// Proceedings of 10th IEEE International Conference on Computer Vision. Beijing, China: IEEE, 2005: 1208-1213.

[7] Yan S C,Xu D, Zhang B Y, et.al. Graph embedding and extension:A general framework for dimensionality reduction[J]. IEEE Trans on Pattern Analysis and Machine Intelligence,2007,29(1):40-51.

[8] 王永茂,徐正光,赵珊. 基于自适应近邻图嵌入的局部鉴别投影算法[J]. 电子与信息学报, 2013,35(3):633-638.

Wang Yongmao, Xu Zhengguang, Zhao Shan. Neighborhood graph embedding based local adaptive discriminant projection[J]. Journal of Electronics and Information Technology,2013,35(3):633-638.

[9] 江艳霞，任波.基于加权邻域极大边界准则的人脸识别[J].数据采集与处理,2011,26(5):515-520.

Jiang Yanxia, Ren Bo. Face recognition based on weighted neighborhood maximum margin criterion[J]. Journal of Data Acquisition and Processing, 2011, 26(5):515-520.

[10]杨利平, 龚卫国, 辜小花,等. 完备鉴别保局投影人脸识别算法[J]. 软件学报,2010,21(6):1277-1286.

Yang Liping, Gong Weiguo, Gu Xiaohua, et al.Complete discriminant locality preserving projections for face recognition[J].Journal of Software,2010,21(6):1277-1286.

[11]殷俊, 金忠. 完备非监督鉴别投影于人脸图像分析[J]. 计算机辅助设计与图像学学报, 2010, 22(11): 1913-1918.

Yin Jun, Jin Zhong.Complete unsupervised discriminant projection and face image analysis[J].Journal of Computer Aided Design and Computer Graphics,2010,22(11):1913-1918.

[12]Wang Y, Wu Y. Complete neighborhood preserving embedding for face recognition[J]. Pattern Recognition, 2010, 43(3):1008-1015.

[13]Raducanu B, Dornaika F. A supervised non-linear dimensionality reduction approach for manifold learning[J]. Pattern Recognition, 2012, 45(6): 2432-2444.

Local Discriminant Projection Algrorithm Based on Complete Adaptive Neighborhood Graph Embedding

Wang Yongmao, Li Geng

(School of Computer Science and Technology, Henan Polytechnic University, Jiaozuo, 454000, China)

The existing adaptive neighborhood graph embedding method based on local discriminant projection(LADP) only uses discriminant information in the principle space of local within-class scatter matrix, which leads to the loss of discriminant information in the null space. To overcome the drawback of LADP, a complete LADP(CLADP) is proposed for face recognition. In the null space of local within-class scatter matrix, irregular discriminant features are extracted by maximizing the local between-class scatter matrix. In the principle space of local within-class scatter matrix, regular discriminant features are extracted by maximizing the local between-class scatter matrix and minimizing the local within-class scatter matrix. Finally, irregular discriminant features and regular discriminant features are combined as the features of CLADP for face recognition. The experimental results on ORL, Yale face database and PIE subset illustrate the effectiveness of the proposed CLADP.

face recognition; adaptive neighborhood graph; local discriminant analysis; complete feature; dimensionality reduction

河南省教育厅科学技术研究(12B520021)资助项目；河南理工大学博士基金(B2014-043)资助项目。

2014-03-05；

2014-05-12

TP391.4