小波去噪算法在含噪盲源分离中的应用*

2015-12-26吴微彭华王彬

数据采集与处理 2015年6期

关键词：盲源小波信噪比

吴微彭华王彬

(解放军信息工程大学信息系统工程学院，郑州，450002)

小波去噪算法在含噪盲源分离中的应用*

吴微彭华王彬

(解放军信息工程大学信息系统工程学院，郑州，450002)

无噪模型下的盲源分离算法在信噪比较低的情况下并不适用。针对该情况一种解决方案就是先对含有高斯白噪声的混合信号进行去噪预处理，然后使用盲源分离算法进行分离。为此，本文提出了一种适用于信噪比较低条件下的基于平移不变量的小波去噪算法。该算法首先使用高频系数滑动窗口法准确估计含噪混合信号的噪声方差，然后使用Bayesshrink阈值估计算法得到更加合理的阈值，最后在不降低去噪效果的同时缩小了平移不变量的范围，减少了运算量。实验仿真表明，在信噪比较低的情况下，与传统小波去噪算法相比，该算法可以更加有效地去除噪声，在很大程度上提升盲源分离算法的性能。

小波阈值收缩算法；平移不变量；含噪盲源分离；贝叶斯收缩算法

引言

盲源分离(Blind sources separation，BSS)是指在多个源的传输过程中，不知源信号和传输通道参数的情况下，仅根据输入源信号的统计特性，由若干个观测信号恢复出源信号的过程。由于无噪条件下的BSS估计问题本身已相当困难[1]，因此很多BSS算法的研究都是在不含噪声的条件下进行的，如广泛使用的快速独立分量分析(Fast independent component analysis，FastICA)[1]和稳健独立分量分析(Robust independent component analysis，RobustICA)[2]等算法。含噪情况下，若信噪比(Signal to noise ratio，SNR)较高，虽然分离后信号的质量有所下降，但这些算法仍然有效。但在信噪比较低的情况下这些算法的分离性能会急剧恶化，甚至完全分离失败，此时已有的无噪BSS算法并不适用。

为了解决含噪盲源分离问题，最直接有效的方法就是对含噪观测信号进行去噪预处理。目前，去噪方法主要有小波去噪、卡尔曼滤波去噪、粒子滤波去噪和曲线阈值去噪等等。对于盲源分离问题而言，几乎无法获得关于原始信号的任何先验信息，因此也无法建立准确的信号模型。而基于小波理论[3-4]的小波去噪算法模型简单，几乎不需要含噪信号的任何先验信息，且小波变换具备良好的时频特性，在去噪领域中也受到了许多学者的重视，并应用小波去噪获得了非常好的效果[5-7]，因此将小波去噪作为含噪盲源分离中去噪预处理方法是十分合适的。然而，小波去噪在信噪比较高时去噪效果较为理想，但在信噪比较低时则会出现较大的偏差。本文主要针对信噪比比较低(0 dB≤SNR≤15 dB)情况下的小波去噪算法进行了深入研究，提出了一种适用于该信噪比区间的小波去噪算法，并将其应用于含噪盲源分离，实验结果表明该算法能够有效去除噪声，显著提升BSS算法的性能。

1 含噪盲源分离概述

1.1 含噪盲源分离模型

含有噪声的盲源分离模型可以描述为

(1)

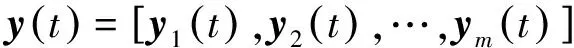
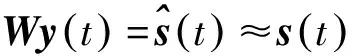
1.2 含噪盲源分离问题解决方案

文献[8]提出了一种基于小波变换的含噪盲源分离解决方案如图1所示。该方法的思路就是将较为复杂的含噪分离问题通过小波去噪预处理转换为相应的无噪分离问题，从而使问题得到简化。文中主要在去噪预处理部分使用了小波阈值收缩算法，并假设噪声方差已知，阈值为极小化斯坦无偏风险估计(Stein′s unbiased risk estimate,SURE)准则。然而，在盲源分离问题中噪声方差通常是无法获得的，并且该文献中没有对小波阈值收缩算法中的参数针对信噪比较低这一条件进行优化。

图1 基于小波去噪的含噪盲源分离解决方案[8]Fig．1 Solution of noisy BSS based on wavelet denoising[8]

本文提出了一种适用于信噪比较低条件下基于平移不变量的小波阈值收缩算法。该算法首先仅使用接收到的观测信号对噪声方差进行估计，然后针对信噪比较低这个前提条件选择合适的阈值估计方法、阈值函数以及循环平移范围。在信噪比较低时，该算法较文献[8]中的方法具有更好的去噪性能，能够进一步提升BSS算法的分离性能。

2 基于平移不变量小波去噪算法的改进

本节首先使用含噪观测信号对噪声方差进行估计，已有的噪声方差估计算法缺乏稳健性，本文提出了一种更加稳健的噪声方差估计算法；其次，对阈值和阈值函数这两个要素在信噪比较低条件下对小波阈值收缩算法性能的影响进行研究，进而选择合适的阈值估计方法和阈值函数；然后针对平移不变量方法中的循环平移量的范围进行研究，在运算量和去噪效果中找到合适的平衡点。

2.1 噪声方差估计的改进算法

(2)

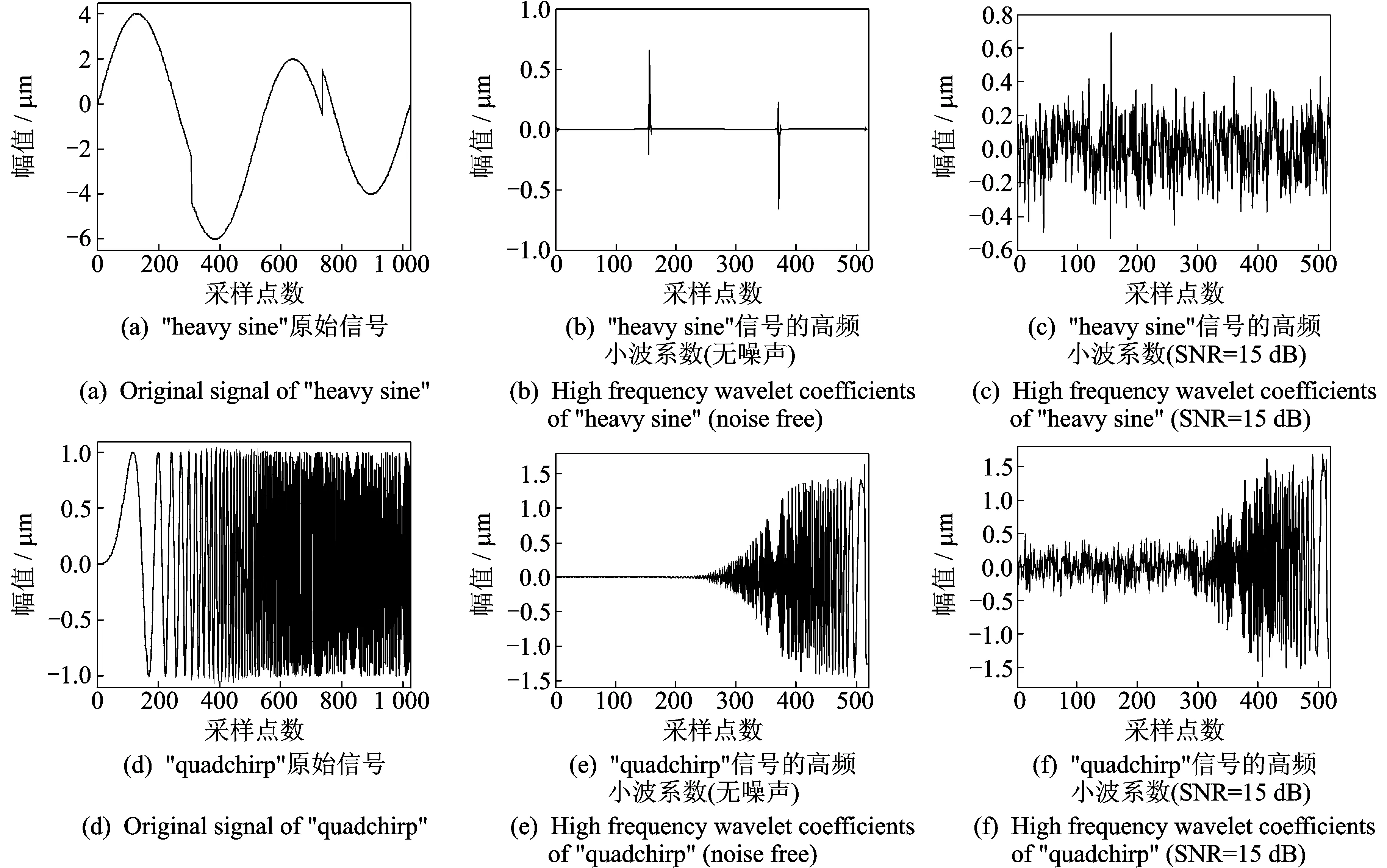
图2 小波高频系数对比示意图Fig．2 Comparison of high frequercy coefficients of wavelet

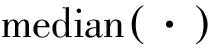
由此，本文对文献[9]提出的方法进行了改进，即在估计噪声方差时不是简单一次性使用所有高频系数，而是在小波高频系数上使用滑动窗口。具体算法描述如下。

(1) 确定初始窗口长度winit和滑动步长sinit。设小波高频系数长度为L，则

(3)

式中[·]表示向下取整。

(5) 根据比值R和Comp2重新设置窗口长度wnew和滑动步长snew。比值R越大或者Comp2越小，窗口长度和滑动步长较初始值增加越多；反之，减小越多。

2.2 阈值和阈值函数

Donoho等提出了小波阈值收缩方法[9]，其主要理论依据是：小波变换特别是正交小波变换具有很强的去相关性，它能够使信号的能量在小波域集中在一些大的小波系数上，而噪声能量分布于整个小波域内。对信号作小波分解后估计出合适的阈值，用阈值处理函数将信号的系数保留或收缩，而使大部分噪声系数归零，用处理后的小波系数重构就得到去噪后的信号。

小波阈值收缩方法中的两个基本要素是阈值和阈值函数。尽管阈值的选取有多种方法，但是并没有一种方法针对任何情况都最优，每种方法都有其自身的特点。统一阈值[9]计算简单，但是其趋向于“过扼杀”小波系数，从而会导致较大的重建误差。最大最小阈值由于基于悲观决策的思想也会“过扼杀”系数。极小化SURE准则[10]和广义交叉验证法[11]在信噪比较高时可以获得较为满意的去噪效果，但是在信噪比较低时其估计得到的阈值则会由于过于“保守”而产生误差，此外，这两种方法的运算量相对较大。文献[12]已经证明BayesShrink阈值能够获得接近于理想阈值的去噪效果。本文主要讨论的是信噪比较低情况下的阈值选取，为此选择BayesShrink阈值，该阈值算法可以在运算量和去噪效果上均获得满意的结果。

在小波阈值收缩方法中，阈值函数体现了对小波系数的不同处理策略，主要分为以下3种：硬阈值函数、软阈值函数和半软阈值函数。一般来说，硬阈值方法可以很好地保留信号边缘等局部特征，但会产生一些间断点；软阈值处理相对要平滑，但会造成一定的高频信息损失。因此，很多学者对半软阈值函数进行了研究，通过参数的设置，使得阈值函数在软阈值与硬阈值之间进行很好的折中，达到更好的去噪效果。然而，由于高斯白噪声污染了所有的小波系数，且贡献相同，而在信噪比较低的情况下，噪声能量较大，噪声对所有小波系数的污染都很严重。由于软阈值函数对每个小波系数都进行了一定的收缩，因此更适合信噪比较低情况下的噪声消除。

2.3 平移不变量小波去噪

小波去噪过程中会产生伪吉布斯现象，这是由于正交小波基不能从多尺度的角度很好地匹配信号的局部结构特征，从而可能使小波变换后的信号产生剧烈振荡的现象。为了有效地消除这种人为的振荡现象，可以使用平移不变量小波去噪方法[13]，该方法是在小波阈值收缩法基础上的改进。

平移不变量小波去噪方法是指在一定的平移量范围内，对所获得的原始信号进行循环平移，对平移后信号作小波变换，再用软或硬阈值对小波系数进行处理，用小波逆变换重构，得到去噪后的新信号，对信号作相反的循环平移，从而得到与原始信号同相位的信号。改变平移量，重复这一过程，对所获结果求平均值。这一平均过程具有很好的去噪性能和光滑性，能很好地逼近真实信号。当平移量的范围是信号长度时称为全平移-平移不变量小波去噪。

对于平移不变量小波去噪中的平移量范围选取，选取范围大，例如全平移-平移不变量小波去噪算法，可以很好地去除伪吉布斯现象，但是运算量非常大；反之，选取范围过小则不能很好去除伪吉布斯现象。因此，需要在运算量和去噪效果之间进行平衡。通过研究发现，随着平移量的增加，去噪性能刚开始提升明显，随后很快趋于一个稳定状态，即当平移量继续增加时，其去噪效果几乎没有改变。实验表明，信号的采样点为1 024时，平移量选取为16时可以获得同全平移-平移不变量小波去噪算法相当的去噪效果。

2.4 一种适用于信噪比较低条件下的小波去噪算法

综上所述，本文提出了一种针对信噪比较低情况下的基于平移不变量的小波去噪算法，算法描述如下。

(1) 对含噪信号进行循环平移，最大平移量为16；

(2) 选定小波基函数和分解层数，对平移后的信号进行小波变换；

(3) 使用小波阈值收缩算法去噪，其中阈值使用BayesShrink阈值，噪声方差使用高频系数滑动窗口法进行估计，阈值函数使用软阈值函数；

(4) 对去噪后的小波系数重构，进行小波反变换，得到重构信号；

(5) 对重构信号进行反向平移，得到一个去噪后的信号；

(6) 判断是否达到最大平移量，若没有，重复步骤(1)～(5)；若已达到最大平移量，对得到的一组去噪后的信号进行平均，即为最终的去噪信号。

3 实验仿真与性能分析

3.1 实验1

为了验证高频系数滑动窗口法估计噪声方差的稳健性，对Matlab中的″heavy sine″，″quadchirp″和″doppler″3个信号分别使用高频系数中值法和高频系数滑动窗口法估计噪声标准差，并同真实的噪声标准差进行比较，信噪比从-4 dB以步长2 dB增加至28 dB，每个实验点重复试验100次，对结果进行平均。得到的结果如图3所示。从图中可以看出高频系数滑动窗口法对于3个信号均可得到满意的结果，因此使用高频系数滑动窗口法估计噪声标准差更加稳健。

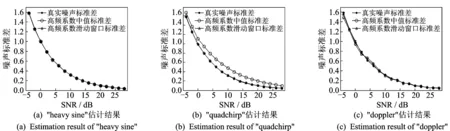
图3 使用不同方法估计噪声标准差结果比较Fig．3 Comparison of estimating noise standard deviation using different methods

3.2 实验2

为了更精确描述算法去噪性能的优劣，这里使用信号均方误差(Signal mean square error, SMSE)作为评判准则，公式如下

(4)

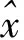
本实验主要对统一阈值、极小化SURE准则、启发式阈值、最大最小阈值、广义交叉验证法和BayesShrink阈值这几种阈值估计算法在信噪比较低情况下的性能进行比较。实验信号取实验1中的3个信号，加入高斯白噪声，使用小波阈值收缩算法进行去噪，这里使用软阈值函数对小波系数进行处理。所选小波为″sym7″，小波变换层数为4。两个信号的采样点数为1 024，信噪比从0 dB以步长为1 dB增加到20 dB，每个实验点重复实验100次，对结果取平均，得到的结果如图4所示。

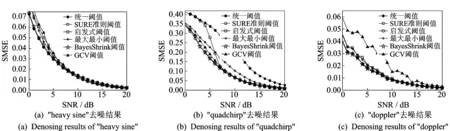
图4 使用不同阈值的去噪结果比较Fig．4 Comparison of denosing results using different thresholds

从图4中可以看出，对“heavy sine”和“doppler”信号的去噪结果中，BayesShrink阈值在0 dB≤SNR≤15 dB区间中均可获得较为满意的结果。而对“quadchirp”信号来说，SURE准则阈值和BayesShrink阈值均可获得满意结果，然而由于SURE准则阈值的计算量较大，因此使用BayesShrink阈值更加合适。综上所述，在信噪比较低的情况下，BayesShrink阈值是最佳选择。

3.3 实验3

为了验证软阈值函数选取的合理性，仍对实验1中的3个信号进行去噪实验，使用BayesShrink阈值算法估计阈值，分别使用软阈值函数、硬阈值函数以及两个半软阈值函数对小波系数进行处理。

半软阈值函数1[14]表达式为

(5)

式中：n为任意正常数，n→∞时阈值函数等效于软阈值函数，n→0时阈值函数等效于硬阈值函数。

半软阈值函数2[15]表达式为

(6)

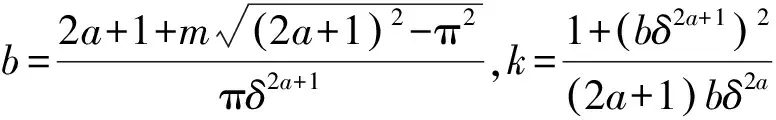
图5 两种半软阈值函数示意图Fig．5 Two half-soft thresholding functions

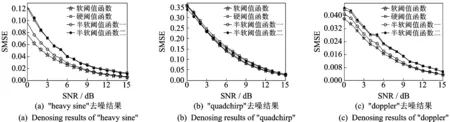
图6 使用不同阈值函数去噪结果比较Fig．6 Comparison of denosing results using different thresholding functions

3.4 实验4

为了验证平移不变量小波去噪算法中的平移范围，进行实验如下：使用BayesShrink阈值算法和软阈值函数，循环平移的采样点数分别为2，4，8，16，32，64，128，256，512和1 024。由于吉布斯效应通常发生在信号起始位置以及不连续点，因此，为了能够更加有效评价该算法对吉布斯效应的抑制效果，仅对去噪后信号的前64个采样点进行比较，得到的结果如图7所示。从图中的比较可以看出，从平移16个采样点开始，平移不变量小波去噪算法的改进效果已不明显，从图中已经较难区分。因此当采样点数为1 024时，选择平移量为16可以获得同全平移-平移不变量小波去噪算法相当的去噪效果，但运算量只有其1/64。

图7 使用不同平移量去噪结果比较Fig．7 Comparison of denosing results using different translation invariant

3.5 实验5

本节的实验主要为了验证将本文提出的改进的基于平移不变量的小波去噪算法应用于含噪盲源分离的有效性。实验安排如下：(1)仅使用经典的FastICA算法和RobustICA算法进行盲源分离；(2)分别使用文献[8]中的小波去噪算法(记为WT)和本文提出的小波去噪算法(记为New WT)对含噪混合信号去噪，然后再使用FastICA算法和RobustICA算法进行盲源分离。

仿真分别使用了两组信号，其中1组由3个亚高斯信号组成，另一组由3个超高斯信号组成。每组信号分别经过随机生成的3×3混合矩阵后，加入高斯白噪声，信号的采样点数为1 024，对混合后的含噪信号使用上述几种方法进行分离。图8是对3个亚高斯信号进行仿真实验，信噪比为5 dB时，仅使用FastICA算法以及先使用本文提出的改进的小波去噪算法进行去噪后再使用FastICA算法进行分离的结果示意图。

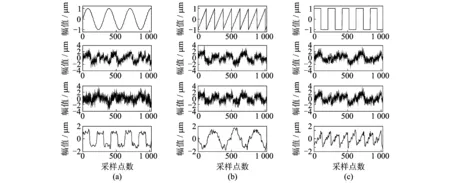
图8 使用FastICA算法时的盲源分离示意图(SNR=5 dB)Fig．8 Comparison of BSS results using FastICA algorithm (SNR=5 dB)

在图8中，第1行是3路原始信号；第2行是3路原始信号经过一个随机混合矩阵后加入高斯白噪声，得到三路含噪混合信号；第三行是仅使用经典的FastICA算法进行分离后得到的分离结果；最后一行是使用本文提出的算法进行去噪后再使用FastICA算法进行分离得到的分离结果。从图中可以直观地看出，仅使用经典的FastICA算法进行分离，分离效果较差，其中锯齿波和正弦波已经无法分辨；而去噪后再进行分离的信号的效果较直接分离的效果显著改善。

图9 几种方法进行含噪盲源分离后结果比较Fig．9 Comparison of separation results using different noisy BSS algorithms

改变信噪比，从0 dB以步长1 dB增加至20 dB，计算分离信号的信号均方误差，每个实验点重复实验100次，对结果取平均，实验仿真结果如图9所示。从图9中可以看出，同文献[8]中的小波去噪算法相比，本文提出的基于平移不变量的小波去噪算法在信噪比较低的情况下性能更好，能够进一步提升盲源分离算法的性能。因此，该方法不失为解决含噪盲源分离问题的一个有效方法。

4 结束语

解决含噪盲源分离问题的一个有效途径就是对含噪混合信号进行去噪，然后使用盲源分离算法进行分离。本文提出的基于平移不变量的小波去噪算法，首先使用高频系数滑动窗口法代替高频系数中值法来估计噪声方差可以得到更准确的噪声方差；其次针对信噪比较低这个条件，对阈值估计算法和阈值函数进行研究，确定使用BayesShrink阈值算法和软阈值函数；再次缩小循环平移范围，较全平移算法而言大幅降低了运算量，而去噪效果几乎没有降低；最后将该算法应用于含噪盲源分离中。实验仿真表明，该算法在信噪比较低的情况下具有更好的去噪性能，能在很大程度上提升盲源分离算法的分离质量。

[1] Hyvärinen A, Karhunen J, Oja E. Independent component analysis[M]. New York: John Wiley & Sons, 2001: 94-112.

[2] Zarzoso V, Comon P. Robust independent component analysis by iterative maximization of the kurtosis contrast with algebraic optimal step size[J]. IEEE Transactions on Neural Networks, 2010, 21(2): 248-261.

[3] Mallat M S. A wavelet tour of signal processing[M]. 3rd Edition. Salt Lake City: Academic Press, 2009: 4-9.

[4] Antoniadis A. Wavelet methods in statistics: Some recent developments and their applications[J]. Statistics Surveys, 2007(1): 16-55.

[5] Ho J, Hwang W L. Wavelet Bayesian network image denoising[J]. IEEE Transactions on Image Processing, 2013, 22(4): 1277-1290.

[6] Boubchir L, Boashash B. Wavelet denoising based on the MAP estimation using the BKF prior with application to images and EEG signals[J]. IEEE Transactions on Signal Processing, 2013, 61(8): 1880-1894.

[7] 郭业才, 康景磊. 形态学算子和小波变换的虹膜去噪算法[J]. 数据采集与处理, 2013, 28(5): 586-590.

Guo Yecai, Kang Jinglei. Suppressing eyelash interference algorithm based on morphology and wavelet analysis[J]. Journal of Data Acquisition and Processing, 2013, 28(5): 586-590.

[8] Paraschiv-Ionescu A, Jutten C, Aminian K. Source separation in strong noisy mixtures: A study of wavelet de-noising pre-processing[C]∥ICASSP′2002. Orlando, Florida: [s.n.], 2002: 1681-1684.

[9] Donoho D L, Johnstone I M. Ideal spatial adaptation via wavelet shrinkage[J]. Biometrika, 1994, 81(3): 425-455.

[10]Donoho D L, Johnstone I M．Adapting to unknown wavelet shrinkage[J]．Journal of the American Statistical Association, 1995, 90(432): 1200-1224.

[11]Jansen M, Malfait M, Bultheel A. Generalized cross-validation for wavelet thresholding[J]. Signal Processing, 1997, 56(1): 33-44.

[12]Chang S G, Yu Bin, Vetterli M. Adaptive wavelet thresholding for image denoising and compression [J]. IEEE Trans Image Processing, 2000, 9 (9): 1532-1546.

[13]Cuevas J P, Chicken E. A trimmed translation invariant denoising estimator[J]. Journal of Statistical Computation and Simulation, 2012, 82(9): 1299-1310.

[14]张维强, 宋国乡. 基于一种新的阈值函数的小波域信号去噪[J]. 西安电子科技大学学报：自然科学版, 2004, 31(2): 296-299.

Zhang Weiqiang, Song Guoxiang. Signal denoising in wavelet domain based on a new kind of thresholding function[J]．Journal of Xi′dian University: Natural Science Edition, 2004, 31(2): 296-299.

[15]刘卫东, 刘尚合, 胡小锋, 等. 小波阈值去噪函数的改进方法分析[J]. 高电压技术, 2007, 33(10): 59-63.

Liu Weidong, Liu Shanghe, Hu Xiaofeng, et al. Analysis of modified methods of wavelet threshold denoising functions[J]. High Voltage Engineering, 2007, 33(10): 59-63.

Application of Wavelet Denoising Algorithm in Noisy Blind Source Separation

Wu Wei， Peng Hua， Wang Bin

(Institute of Information System Engineering, PLA Information Engineering University, Zhengzhou, 450002, China)

Blind source separation (BSS) algorithms based on the noise-free model are not applicable when the SNR is low. To deal with this issue, one way is to denoise the mixtures corrupted by white Gaussian noise, firstly, and then utilize the BSS algorithms. Therefore, a Waveshrink algorithm is proposed based on translation invariant to denoise mixtures with strong noise. The high-frequency coefficients sliding window method is utilized to estimate the noise variance accurately, and BayesShrink algorithm is utilized for a more reasonable threshold. Consequently, the scope of the translation invariant is narrowed without degrading the performance of denoising, thus reducing the computation amount. Simulation results indicate that the proposed approach perform better in denoising compared with the traditional Waveshrink algorithm, and can remarkably enhance the separation performance of BSS algorithms, especially in the case with low signal SNRs.

waveshrink algorithm; translation invariant; noisy blind source separation; BayesShrink algorithm

国家自然科学基金(61401511)资助项目。

2013-09-11；

2014-03-21

TN911.7