深孔内径的在线精密测量原理及系统

丁正龙,徐月同,傅建中

(浙江大学流体动力与机电系统国家重点实验室,310027,杭州)



深孔内径的在线精密测量原理及系统

丁正龙,徐月同,傅建中

(浙江大学流体动力与机电系统国家重点实验室,310027,杭州)

针对深孔零件内径测量精度要求高、测量空间受限的问题,利用机械测量转换机构和电感位移传感器,研制了一种深孔内径在线精密测量装置。首先对测量转换机构进行力学分析,推导出影响该机构测量精度的主要因素,然后提出一种针对该装置系统的误差补偿方法,并搭建了在线测量平台,最后将测量装置安装在自动化生产线上,在工作状态下对某已标定深孔内径尺寸的工件进行多次重复测量实验,根据六西格玛理论对该测量系统进行统计学分析。分析结果表明:为了提高系统的测量精度和动态特性,转换机构设计时应该选择较大的刚性比和合理的簧片高度,以保证较小的寄生转角和较大的固有频率。实验结果表明:测量系统偏倚为0.02 μm,测量极差为2 μm,测量精度为3 μm。该装置具有结构简单、测量精度高的优点,能够满足深孔内径在线测量要求。

深孔;内径测量;转换机构;寄生转角;误差补偿

深孔内径测量是长度测量中的关键技术之一。自动化生产线在线测量环境较为恶劣,测量精度影响因素众多,受工作环境与测量空间的限制,高精度传感器一般很难直接安装到被测孔内进行自动化测量,因此如何高精度、高效率地测量深孔内径一直是行业技术难题[1]。

目前,针对深孔内径测量问题的研究主要分为非接触式测量和接触式测量两个方向。非接触式测量在工业测量中已广泛应用,例如综合运用电子学、光电探测以及图像处理等技术的工业视觉检测[2-7]。但是,采用高精度非接触式方法测量深孔内径时,对测量环境要求比较高,所需要的系统也比较复杂,使附加成本急剧上升,在工业在线检测实践中难以推广[8-9]。此外,三坐标测量机和触发式测头在工业实践中也有广泛应用,但是三坐标测量机由于设备灵活性低,一般适用于线下测量;触发式测头容易受机床自身精度影响,一般用于高精度机床的机内测量。在检测机构设计中,悬臂梁机构由于结构简单,可靠性好,已有广泛应用[10-13]。传统的悬臂梁结构多用在三维测头上,导向范围比较小,寄生转角所引起的导向误差为纳米级,可忽略不计,但是为了适应深孔内径高精度测量,必须增加测量臂的长度以及平动板行程,误差经过测量臂放大后,对实际测量数据的影响需要进行精确分析和补偿。

本文利用机械结构稳定性好的特点,结合高精度的电感位移传感器,设计出一种深孔内径测量转换机构,然后通过力学分析推导出测量精度的主要影响因素,继而提出一种误差补偿方法,并以此理论为基础制造出转换机构实体,搭建了在线检测量平台进行测量实验,进行了统计学分析。实验结果表明,该深孔内径测量系统具有结构简单、反应灵敏、导向精度高和结构紧凑等优点,提高了深孔类零件在线检测效率和精度。

1 转换机构工作原理

图1所示为测量转换机构简图,实线所示为簧片在外力作用下处于大变形状态,即初始状态,双点划线所示为测量状态。为便于测量臂进入孔内测量,测量前在外力作用下平动板带动测量臂向内收缩;待测量臂进入孔内时,撤去外力,此时簧片恢复力大于弹簧力,平动板随着簧片沿孔径向往外运动,直到两个测头皆与工件内孔表面接触后才停止运动,传感器测出平动板水平方向位移,结合两个转换机构传感器的数据,得出工件孔径尺寸。

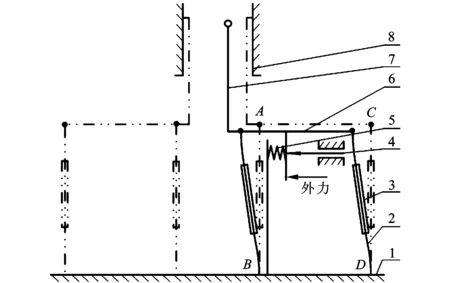
1:测量平台;2:簧片;3:刚性夹板;4:传感器;5:弹簧;6:平动板;7:测量臂;8:内孔表面图1 转换机构简图

在理想状况下,测量过程中簧片AB、CD发生的弹性变形完全相同,平动板相对于测量平台做平动。在实际测量过程中,由于簧片AB、CD受力变形情况并不相同,平动板会发生微小角度旋转,称该转角为寄生转角α。

2 转换机构力学分析

2.1 转换机构受力分析

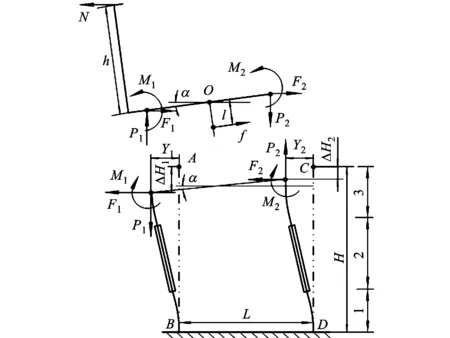
图2 转换机构受力分析示意图

图2所示为转换机构工作时受力分析示意图,在不影响结果的前提下,为了简化模型,把测量臂、平动板以及刚性夹板设为刚性,忽略重力作用。簧片AB在水平方向的力F1、弯矩M1以及垂直方向上的压力P1的共同作用下,产生向左偏转和压缩变形;簧片CD在水平方向的力F2、弯矩M2以及垂直方向上的拉力P2的共同作用下,产生向左偏转和拉伸变形。由于两簧片变形量不同,导致平动板发生寄生旋转,两簧片在水平方向的变形量分别为X1、X2,在垂直方向的变形量分别为ΔH1、ΔH2,簧片总高度为H,弹簧预紧力为f,弹簧作用点与中心点O的距离为l,测量臂高度为h,两簧片间距离为L,簧片中间刚性夹板长为a,簧片上下柔性部分长度皆为b。

2.2 簧片挠曲变形分析

簧片AB和CD结构相同,可以简化为单个悬臂梁进行分段建模。为了便于求解,将簧片分为上中下3段,其中上下两段均为弹性体,弹性模量为E,中间段为刚性体,如图3a所示,此处由于垂直分力P对簧片挠曲变形影响较小,可以忽略。ω为挠度,β为簧片变形转角,由于簧片是由3段组合而成的,根据挠曲线方程(1)和叠加法求解弯曲变形[14],可以得到簧片挠度和转角分段函数,如式(2)～(4)所示,具体分段过程参见图3。

(a)簧片整体挠曲变形

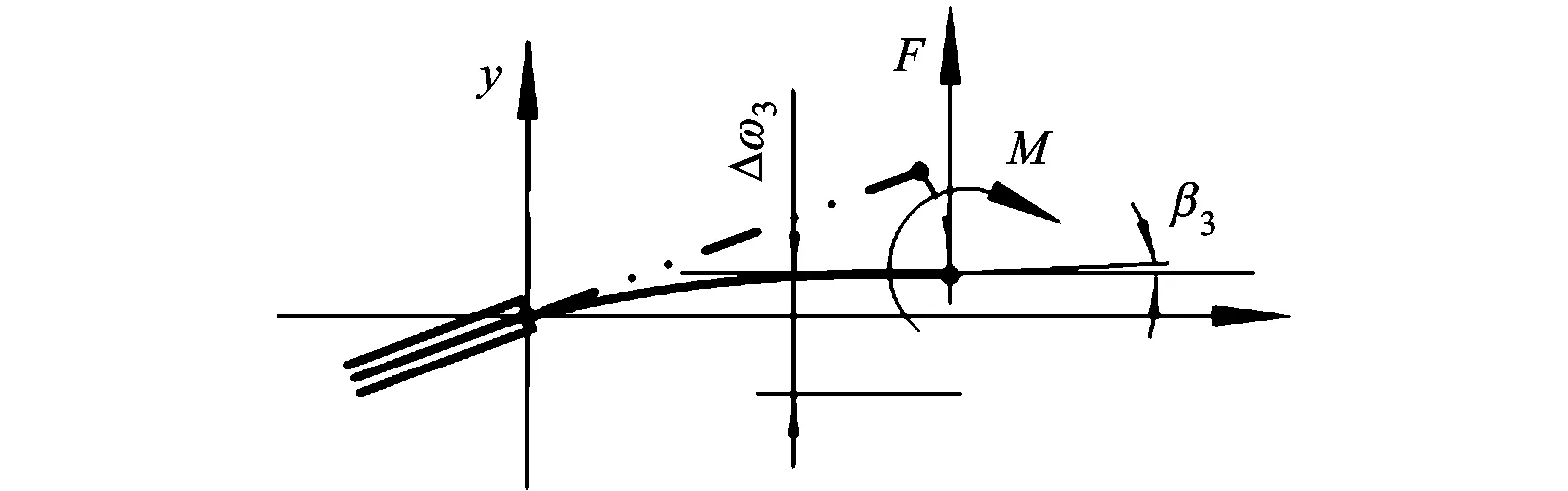
(b)第3段簧片挠曲变形图3 悬臂梁简化模型示意图

挠曲线方程为

(1)

(1)当x∈[0,b)时,由叠加法求解弯曲变形可得ω1=ωF1+ωM1,ωF1、ωM1分别表示力F和力矩M对第1段簧片作用所产生的挠度;β1=βF1+βM1,βF1、βM1分别表示力F和力矩M对第1段簧片作用所产生的转角;由挠曲变形公式可得簧片第1段的挠度ω1和转角β1的表达式如下

(2)

(2)当x∈[b,H-b)时,簧片为刚性,此时簧片挠度由两部分组成,一部分为b点挠度,另一部分为转角α引起的刚性部分的位移(x-b)tanβb。在该区间内转角为常数,且b点处转角连续,即β1(b)=β2(b),根据叠加法求解弯曲变形公式和挠曲变形公式,可推导出该段簧片挠度ω2和转角β2的表达式如下

(3)

(3)当x∈[H-b,H]时,对机构整体分析可知,平动板寄生转角远小于簧片挠曲变形后的转角,因此簧片顶端挠度方向和转角方向与前两段相反,根据叠加法求解弯曲变形公式和挠曲变形公式,可推导出该段簧片挠度ω3和转角β3的表达式如下

(4)

由于簧片顶端与平动板固定,即簧片顶端挠度ω(H)=Y,记Y为簧片顶端测量位移;转角β(H)≈0,又ω(0)=0,β(b)=β(a+b),代入式(4)可推出簧片所受力与力矩,如下式所示

(5)

2.3 求解平动板寄生转角

根据图2所构建的分析模型,对机构整体分别进行几何和力学分析,列出变形协调方程,得到下式

(6)

(7)

当α趋于很小时,sinα≈α,cosα≈1,则式(6)和式(7)可以简化为式(8)和式(9)

(8)

(9)

在机构中,簧片变形由挠度变形和拉压变形组合而成,其沿x轴方向的变形量为

(10)

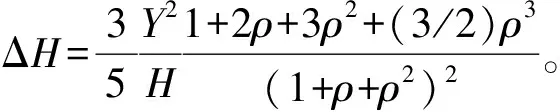
联解方程组(9)和(10)可得

(11)

联解方程组(4)、(8)、(9)和(11),可以得到平动板的寄生转角为

(12)

2.4 转换机构动力学特性分析

转换机构AB和CD上各有2段小簧片,对测量过程中某一簧片进行分析,将簧片整体简化为伪刚体模型,建立如图4所示的坐标系。

图4 簧片受力伪刚体模型

单个簧片在载荷作用下的弹性势能可表述为V=kβ2/2,整个转换机构的总势能如下

VT=(m1+m2)gH+2kβ2

(13)

式中:m1为平动板质量;m2为刚性夹板质量;k为簧片刚度系数。在簧片上取任意一点(x,y)对时间求导,可以得出该点速度,然后对簧片进行动能积分。由2.2小节的边界条件可知,单个簧片的动能T=mb2β2/2,因此整个转换机构的总动能如下

(14)

式中:m为簧片单位长度质量;J为刚性夹板的转动惯量。由式(13)、(14)及系统Lagrange函数可知,转换机构的动力学方程为

(15)

由式(15)可知系统固有频率为

ωn=[(4k-2mb2)/(m1H2+2J)]1/2

(16)

由上式可知,系统固有频率受簧片性能参数(见表1)影响较大:①簧片长度b越小(刚性比ρ越大),固有频率ωn越大;②簧片几何参数确定时,固有频率ωn随簧片刚度k的增加而增加;③簧片高度H增大,固有频率ωn减小。

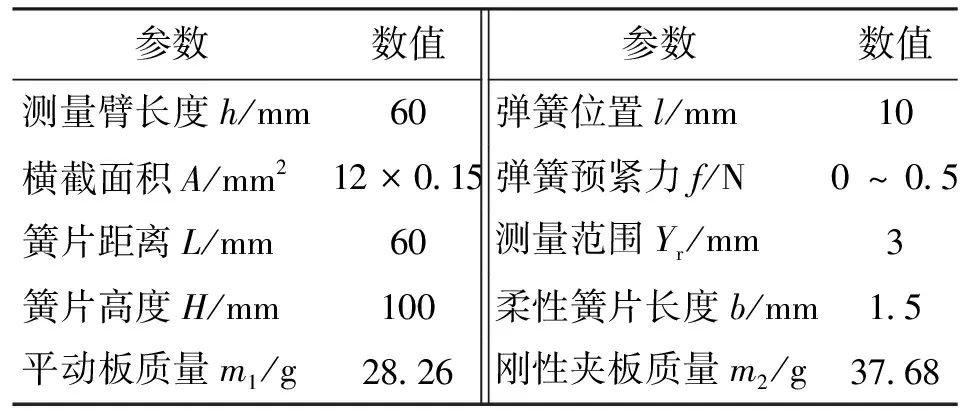
表1 转换机构物理参数

将表1参数代入式(16)中,其中簧片机构所选材料的弹性模量E为128 GPa,泊松比μ为0.3,得出ωn=2.7 kHz,远大于生产线振动频率。在实际测量过程中,未发现共振现象,检测装置采样时间为4 s,动态特性能够满足生产线在线检测要求。

3 转换机构误差研究

测量转换机构误差主要由机构安装误差、测头补偿误差以及平动板导向误差3部分组成。机构安装误差δ1是指测头中心轴线与工件中心平面的偏差,一般通过千分表进行手工调整或者通过软件进行补偿。测头补偿误差δ2是指测头规划位置和测头实际位置存在的偏差,可采用在线标定技术建立测头补偿的误差列表,然后采用双线插值运算得到测头球面任意位置法矢信息和测头半径补偿值,再根据法矢信息找到对应的误差值进行对应补偿[16]。

3.1 平动板导向误差分析

平动板导向误差是通过平动板寄生转角α来表达的,α越小,则导向精度越高。因此,可以通过间接分析测量转换机构各参数对寄生转角的影响,来分析平动板导向误差。由式(12)可知,在保证足够测量位移Y的前提下,为了减小转换机构导向误差,提高测量精度,可以适当增加两簧片间距离L和簧片柔性部分横截面积A,亦可以合理减小弹簧的预紧力f。图5所示为寄生转角α与测量位移Y之间的关系。由图可知,在Y及其他参数一定的情况下,簧片越高,平动板寄生转角越小,但当簧片高度H达到一定值时,继续增加H对寄生转角的影响逐渐减小。由式(16)可知,ωn随H的增大而减小。因此,在满足导向精度的前提下,应该合理地选择H,以提高系统的抗干扰能力。

图5 寄生转角与测量位移之间的关系

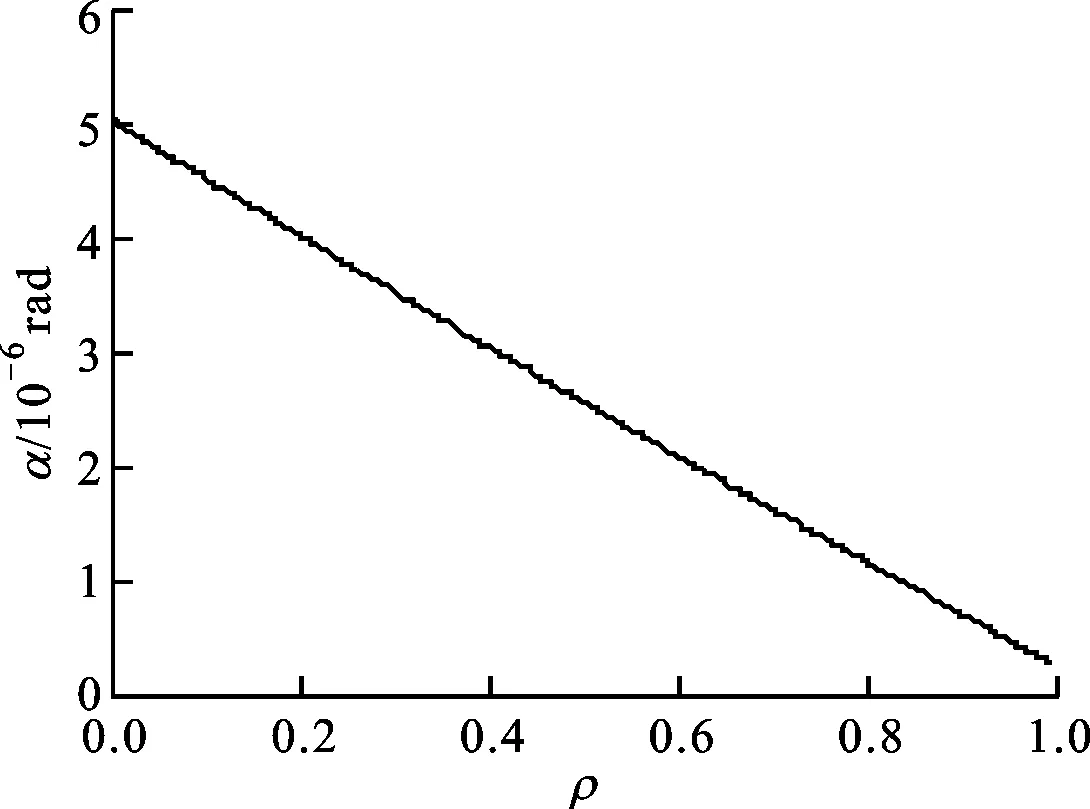
图6 寄生转角与簧片刚性比之间的关系

比较图5和图6可知,在其他参数一定时,ρ比Y所引起的寄生转角大10倍左右。因此,在综合考虑各参数对ωn和α的影响程度后,合理地选取转换机构各主要参数,得到较小的α,并计算出寄生转角所引起的平动板导向误差

δ3=(h+l)α

(17)

3.2 误差补偿

由上述误差分析可知,补偿后工件内孔直径可以表达为

YR=YM+δ1+δ2+δ3

(18)

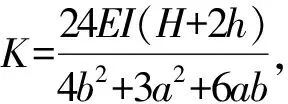
(19)

工控机在获得测量数据后,补偿上述3种误差,即可得到工件实际尺寸,总体误差补偿流程图如图7所示。

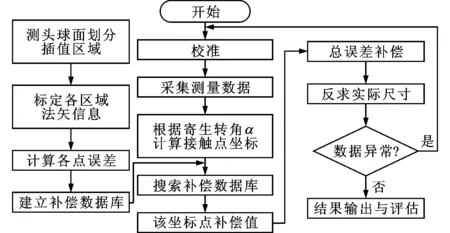
图7 误差补偿流程图

3.3 实验验证

在上述理论基础上设计并搭建了测量装置样机,如图8所示(为了便于表达,图中省去装夹具),具体参数见表1。将测量装置安装在自动化生产线上,如图9所示,其中电感传感器分辨率为0.5 μm。

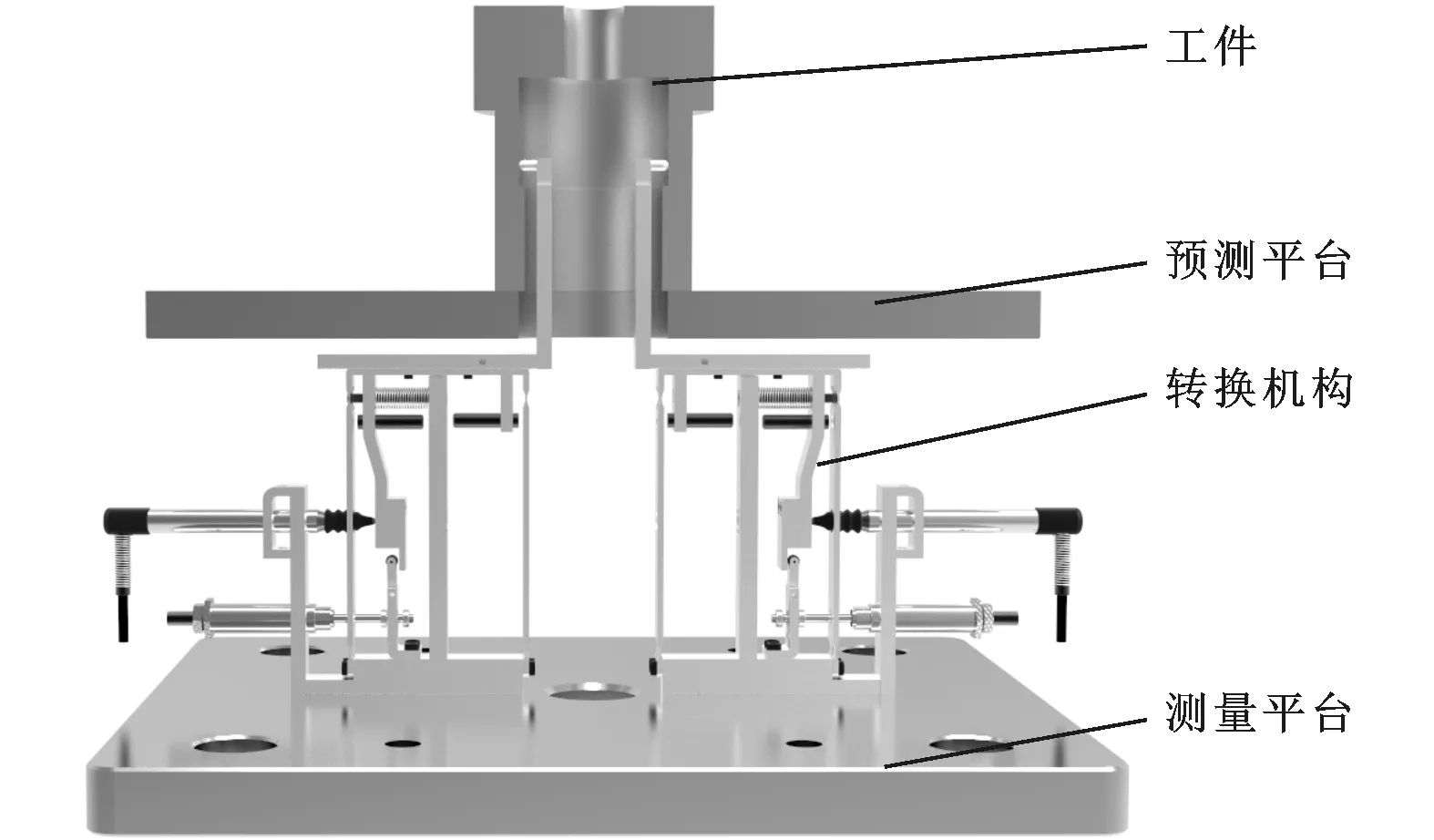
图8 测量装置示意图

在生产线正常工作状态下,对某孔径YB为52.001 mm、孔深为300 mm的零件进行测量实验,实验分为20组,每组分别进行5次测量,测量结果如表2所示。

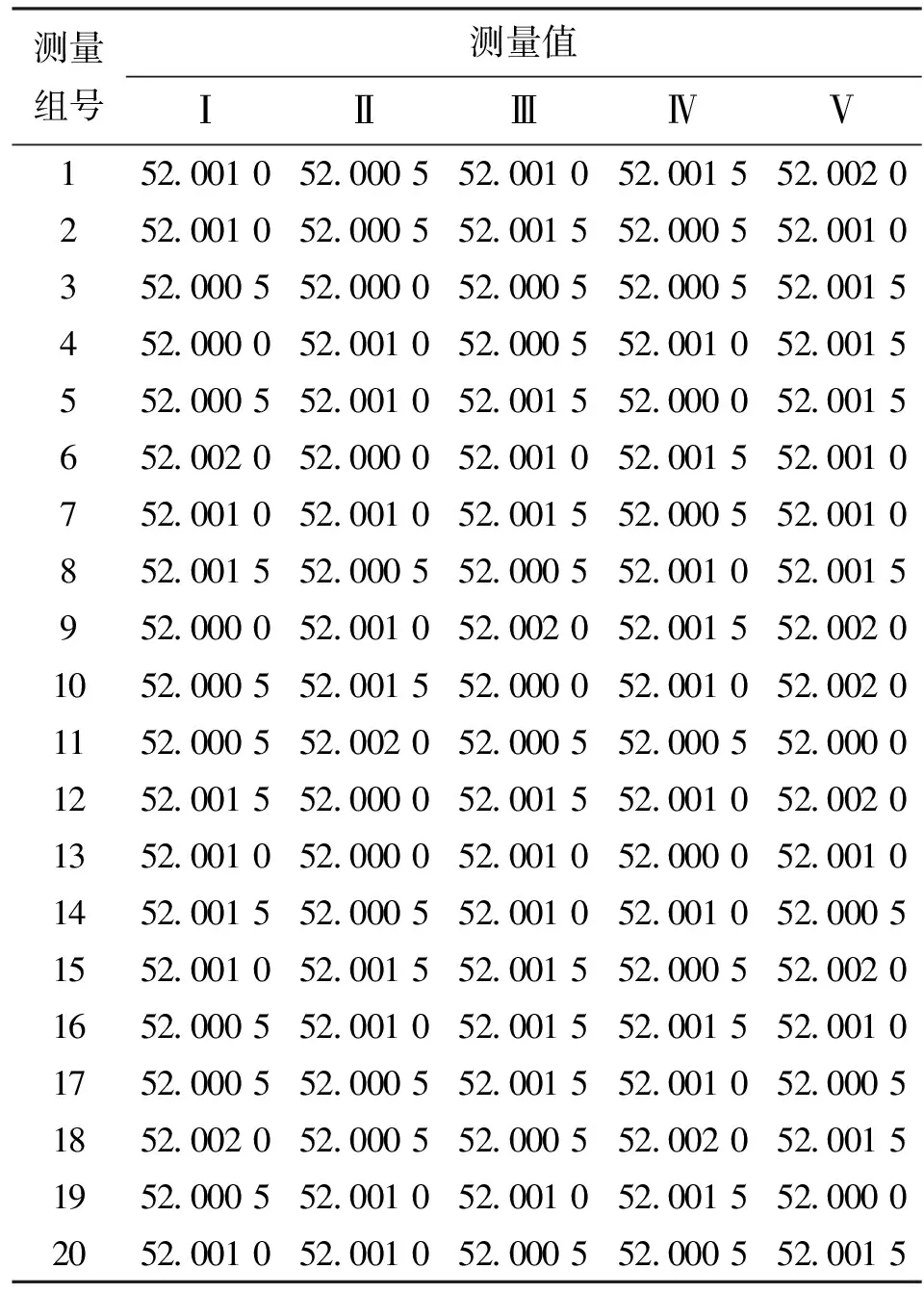
表2 测量结果 mm

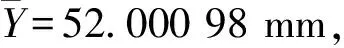
(20)

4 结 论

通过对深孔内径测量转换机构建立整体数学模型,并对转换机构中簧片提出分段建模,然后进行力学和几何分析,找出了测量机构工作过程中影响测量精度的主要因素有两簧片间距离L、簧片的横截面积A、弹簧的预紧力f、簧片高度H、簧片刚性比ρ以及测头半径补偿误差δ2;最后,提出一种误差补偿方法,并搭建了深孔内径测量平台,对理论进行了实验验证。实验结果显示,深孔内径测量系统误差为0.02μm,测量极差为2μm,测量精度为3μm,表明该测量系统具有结构简单、反应灵敏以及测量精度高等优点,有效地解决了深孔内径测量问题。

[1] MA Y Z, YU Y X, WANG X H. Diameter measuring technique based on capacitive probe for deep hole or oblique hole monitoring [J]. Measurement, 2014, 47: 42-44.

[2] SHAHABI H H, RATNAM M M. Assessment of flank wear and nose radius wear from workpiece roughness profile in turning operation using machine vision [J]. International Journal of Advanced Manu-facturing Technology, 2009, 43(1/2): 11-21.

[3] 裘祖荣, 陈浩玉, 胡文川, 等. 基于嵌入式的角度视觉检测及误差补偿 [J]. 光学精密工程, 2013, 21(10): 2480-2487. QIU Zurong, CHEN Haoyu, HU Wenchuan, et al. Embedded angle vision inspection and error compensation for line structured lights [J]. Opt Precision Eng, 2013, 21(10): 2480-2487.

[4] RIBY A B, PRASHANT S, SONAKAR M, et al. Identification of defects on highly reflective ring components and analysis using machine vision [J]. International Journal of Advanced Manufacturing Technology, 2011, 52(1/2/3/4): 217-233.

[5] YU Y X, ZHANG H, WANG Z C, et al. Deep-hole inner diameter measuring system based on non-contact capacitance sensor [J]. Transactions of Tianjin University, 2010, 16(6): 447-451.

[6] 叶树亮, 谭久彬. 基于动态阿贝原则的高精度激光深孔内径测量 [J]. 光电子·激光, 2008, 8(15): 971-974. YE S L, TAN J B. High precision laser deep hole diameter measurement based on dynamic Abbe’s prin-ciple [J]. Journal of Optoelectronics·Laser, 2008, 8(15): 971-974.

[7] 王家贵, 李林峰. 基于迈克尔逊干涉原理的孔径测量及装置设计 [J]. 工具技术, 2013, 47(4): 58-60. WANG Jiagui, LI Linfeng. Aperture measurement which based on Michelson interference principle and design of device [J]. Tool Engineering, 2013, 47(4): 58-60.

[8] STONE J, MURALIKRISHNAN B. Geometric effects when measuring small holes with micro contact probes [J]. Journal of Research of the National Institute of Standards and Technology, 2011, 116(2): 573-587.

[9] HRIOSHI M, AKIO K, HIROMICHI O. Development of a system for measuring micro hole accuracy using an optical fiber probe [J]. Journal of Advanced Mechanical Design, Systems and Manufacturing, 2010, 4(5): 995-1004.

[10]刘宇, 段耀宇, 刘利, 等. 悬臂梁陀螺仪机械性能优化及系统实现 [J]. 光学精密工程, 2012, 20(9): 2051-2059. LIU Yu, DUAN Yaoyu, LIU Li, et al. Mechanical performance optimization and system implementation of cantilever beam gyroscope [J]. Opt Precision Eng, 2012, 20(9): 2051-2059.

[11]赵立波, 徐龙起, 热合曼艾比布力, 等. 矩形微悬臂梁的流固耦合谐振频率分析 [J]. 西安交通大学学报, 2013, 47(11): 60-64. ZHAO Libo, XU Longqi, RAHMAN Hebibul, et al. Resonant frequency of the rectangular micro-cantilever in fluid-structure interaction [J]. Journal of Xi’an Jiaotong University, 2013, 47(11): 60-64.

[12]乔龙学, 王伟刚, 何姗. 双悬臂梁直径测量传感器性能分析 [J]. 浙江大学学报: 工学版, 2012, 46(6): 1060-1066. QIAO Longxue, WANG Weigang, HE Shan. Perfor-mance analysis on twin-cantilever transducer for measuring diameter [J]. Journal of Zhejiang University: Engineering Science, 2012, 46(6): 1060-1066.

[13]崔岩, 张吕权, 夏劲松, 等. 压电微悬臂梁探针的制作工艺研究 [J]. 西安交通大学学报, 2011, 45(1): 79-82. CUI Yan, ZHANG Lvquan, XIA Jinsong, et al. Fabrication of novel piezoelectric microcantilever probe [J]. Journal of Xi’an Jiaotong University, 2011, 45(1): 79-82.

[14]闫晓鹏, 武瑛. 材料力学 [M]. 北京: 清华大学出版社, 2013.

[15]MURANAKA Y, INABA M, ASANO T, et al. Parasitic rotation in parallel spring movements [J]. Int J Jpn Soc Pre Eng, 1991, 25(3): 208-213.

[16]王立成, 黄兴达, 丁汉. 原位检测系统中触发式测头的误差分析与补偿 [J]. 中国机械工程, 2012, 23(15): 1774-1778. WANG Licheng, HUANG Xinda, DING Han. Error analysis and compensation for touch trigger probe of on-machine measurement system [J]. China Mechanical Engineering, 2012, 23(15): 1774-1778.

[17]马逢时, 周暐, 刘传冰. 六西格玛管理统计指南 [M]. 北京: 中国人民大学出版社, 2013.

[本刊相关文献链接]

李朝辉,王昭,黄军辉,等.滚转角测量中直角棱镜相位损失及解决方法.2014,48(9):112-116.[doi:10.7652/xjtuxb2014 09019]

彭希锋,王玲,杨文剑,等.自适应优化控制的人工髋关节磨损三坐标测量及评估方法.2014,48(8):128-135.[doi:10.7652/xjtuxb201408022]

俞珏,庄健,于德弘.采用李雅普诺夫函数的电液伺服系统反馈线性化控制.2014,48(7):71-76.[doi:10.7652/xjtuxb 201407013]

杨军,施虎,梅雪松,等.双驱伺服进给系统热误差的试验测量与预测模型构建.2013,47(11):53-59.[doi:10.7652/xjtuxb201311010]

曹建安,张乐平,吴昊,等.采用倾角传感器实现空间旋转角度测量的解析方法研究.2013,47(10):109-114.[doi:10.7652/xjtuxb201310019]

吕涛,刘志刚,邓忠文,等.一种光纤组量程扩增的激光频率扫描干涉绝对测距系统.2013,47(9):77-82.[doi:10.7652/xjtuxb201309013]

钟丽红,王昭,汤善治,等.机床滚转角测量中敏感元件倾斜引起的误差分析.2013,47(5):99-103.[doi:10.7652/xjtuxb 201305018]

邓玉芬,郭俊杰,王金栋,等.激光跟踪仪在重型车床几何精度检测中的应用.2013,47(1):74-79.[doi:10.7652/xjtuxb 201301015]

韩有昂,张英杰,喻明让.一种有向投影的测量数据刀具轨迹生成技术.2011,45(9):11-14.[doi:10.7652/xjtuxb2011 09003]

张维光,赵宏.线结构光多传感器三维测量系统误差校正方法.2011,45(6):75-80.[doi:10.7652/xjtuxb201106014]

(编辑 荆树蓉)

On-Line Precise Measurement Principle and System for Deep-Hole Diameter

DING Zhenglong,XU Yuetong,FU Jianzhong

(The State Key Lab of Fluid Power Transmission and Control, Zhejiang University, Hangzhou 310027, China)

Considering the requirement on the high-precision measurement of deep-hole diameter with limited measuring space, a precise on-line measurement device for deep-hole diameter was designed using the mechanical measurement transformation mechanism and the inductive displacement transducer. First, the mechanics analysis of the measurement transformation mechanism was performed and the main factors affecting the measuring accuracy were deduced. Then, a method of systemic error compensation for the device was proposed, and the on-line measurement platform was set up. Finally, the measurement device was installed on the automatic production line, and the measuring experiments were carried out repeatedly to measure the calibrated inner hole diameter of a workpiece. The statistical analysis of the measurement system was performed based on the theory of Six Sigma. The analysis results suggest that in order to improve the measuring accuracy and dynamic performance of the system, a larger rigid ratio and a reasonable reed height should be chosen to ensure a smaller parasitic rotation and a higher natural frequency when the transformation mechanism is designed. The experimental results suggest that the system bias is 0.02 μm, the range is 2 μm and the measuring accuracy is 3 μm. The device has the advantage of simple structure and high precision, which meets the requirements of on-line measurement of deep-hole diameter.

deep-hole; diameter measurement; transformation mechanism; parasitic rotation; error compensation

2014-06-09。

丁正龙(1988—),男,硕士生;傅建中(通信作者),男,教授,博士生导师。

国家科技支撑计划资助项目(2013BAF05B00)。

时间:2014-10-15

10.7652/xjtuxb201501011

TH822;TH135

A

0253-987X(2015)01-0065-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20141015.1751.001.html