后方交会测量精度影响冈素研究

2016-03-22付海珊

科技传播 2016年1期

付海珊

摘要交会测量是控制点加密的常用方法，由未知点向控制点观测进而得出未知点坐标的后方交会法，其应用非常的广泛，所以对其精度的研究应更加得到关注，本文从角度，边长，边角同测的后方交会的近似精度评定公式和考虑起算的数据存在误差时的严密精度评定式出发，分别讨论三种不同的后方交会的精度影响因素，并关注这些因素的变化从而导致待定点精度的变化。最后通过实验实例，分别对边长，角度，边角同测等后方交会的精度及坐标进行分析与比较。

关键词后方交会；测量平差；精度分析

中图分类号 S29

文献标识码 A

文章编号 1674-6708（2016） 154-0049-03

在测量中常常遇到控制点因建筑物阻挡等其他原因造成不能通视，不得不临时增设测量点来进行测量或工程施工放样。加设控制点方法有许多，一种较好的方法是在视野辽阔、通式条件好且不容易受到毁损的未知点上用全站仪向已知点进行观测的后方交会，经研究发现，角度、距离、控制点个数的变化对其精度有很大的影响，本文通过对常用后方交会的原理及精度评定出发，通过数学演算得出这些影响因素是如何影响其精度的，然后在野外进行试验从而验证这些规律，本文最后结合工程实例，通过后方交会解算的精度影响因素研究，从而提高未知点精度，进而提高工程质量。

1 后方交会

1.1 定义

定义1（测角后方交会）：后方交会是指仅在未知点P上架设仪器，向最低三个或三个以上的已知控制点4、B、C观测两个水平夹角a，B，从而计算未知点的坐标。

由于测距仪以及全站仪逐渐的广泛使用，后方交会还有如下的两种解释：边长角度同测的后方交会以及仅仅测边后方交会。

定义2（测边后方交会）：在未知点P上向控制点，观测两个水平距离PA、PB的边长以、6，再利用三边求解三角形，从而加密P点的坐标。

定义3（边角同测后方交会）：在未知的控制点上P上安置仪器，再向已知点A、β观测两个边长的距离以及水平角y，进而求得P点的坐标。

1.2 计算原理

后方交会计算的方法种类有很多，不同种类的后方交会的计算方法也尽不相同。

1.2.1 测角后方交会

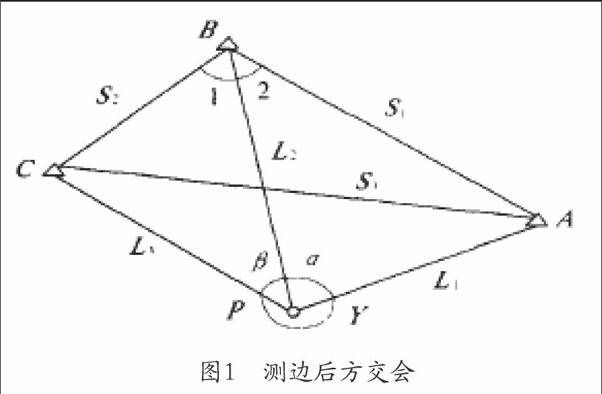
如下图的图l表示，已知A、B、C三点的坐标分别为A（Xa，Ya）、B（Xa，Ya）、c（x，，y），观测角度分别为a，β，再求待定点P的坐标（Xa，Ya）。

1.2.2边角后方交会

随着全站仪的全面普及，边角同测在测量中用的越来越广泛，其计算可分为以下两种情况，第一种情况如图2，A、β位已知点，所以A点与B点的距离SAB以及方位角aBA为已知。观测量为PB的边长S以及LAPB的角度B。显然在这样的图形中观测边位于观测角的右边。

1.2.3测边后方交会

仍在图1中，S、s：、S3为三角形的已知边长，厶1、厶2、厶3为测量的边长，厶1、厶2为辅助角，求待定点的坐标P （xp，yp）。从理论上来说，只需要两点的后方距离交会就可计算未知点P的坐标，当有3个已知点或更多点存在时候，则存在一个或对个多余观测。

2 精度影响因素的研究

2.1 角度后方交会的影响因素

在角度后方交会中（或三点后方交会），如图1。其P点的X、Y方向的坐标精度，即不考虑初始数据误差的影响，故P点的坐标中误差为：

故P点的坐标的精度就可用参数K1、K2、K3来显现。由于K1、K2、K3是通过观测的角度变化而变化的，且K1、K2、K3可有引数查表，所以m，的值与交会点P相对于已知点的位置（图形位置）有关，且与观测角度的位置有关。

2.2 边长后方交会的影响因素

在前面的计算与精度评定中，已推算出P点的X、y方向的精度表达式，所以P点的点位中误差为：

现在考虑全站仪的标称误差，即：m2s a2+（6*s）2，式子中，a为固定误差；b为比例误差，以毫米（ mm）为单位；S为测距的边长值，以千米（km）为单位。

正常情况下，在工程测量中，所测的边长大多在lkm到2km之内，所以当交会点点位分布适宜，所测的两条边的距离其差值不会很大（大多数在lkm之内），这样按标称误差的公式估算，两条测边的m，值和m。值非常接近，故对于精度的约算来说，从而可以来说两条所测的测边精度一样或大约一样，即：所以P点的误差又可以写成如下面的式子：

从以上的推导式子可以看出测边后方会的影响因素主要由交会角度y、仪器的标称精度以及所测的距离有关，具体是如何影响其精度也将在后面的实验中呈现出来。

2.3 边角同测后方交会的影响因素研究

将上式中的（7）式进一步简化，得到如下式子：

从公式可以看出，边角后方交会的精度与测角、测边以及交会图形有关，现在我们作以下式分析。

1）当y =90。时，此时m2，=oo，所以边角后方交会测量中应当尽量避免三角形中并未测量的边长与已知边相垂直或者大约垂直。即y应避免在75。到90。之间的区域。

2）当y=0。时，此时m，的值最小，所以在边角后方交会的布设图形中其角度y应该< 30。为宜。当待定点P在已知边上或者其延长线上的时候，m2，的值主要决定于值的大小。由极值理论知，当s1=s2时，s1与s2的相乘的结果最大，故当未知的点P在已知边附近，且离已知点较近时候，为边角同测的后方交会的最适宜布设点位的空间。

3）若取3=5+5 ppm，m=+10”，S。=l.Okm.可以计算不一样的s1或s2以及y角所决定的边角同测的后方交会图形中的点位精度。故可画出点位误差的等值线图。

3 实验及数据分析

3.1 实验概况

实验实例：为了研究各后方交会中的影响因素时如何影响其精度的，现在在学校的西南角取实验场地，按照以上原理方法现场模拟，按照图1的图形模拟实验，用不同的方法取得不同的数据，按照公式求得未知点坐标，再研究其是如何变化，并绘制误差等直线图。

实验的控制点和未知点的观测均使用科利达全站仪仪器，且控制点坐标均为假设，该仪器经检定达到使用精度的要求，并在有限期之内。其观测角的精度为0 5”，测距的精度为0.5mm+lx 10-6d。

3.2 角度后方交会的分析

现按图1的形状假设仪器，分别测定三个方向值，从而就可以解算出夹角a，β。再按三角形基本知识进而求得S角度，由于m，的值可由K表示，如式K=将其转为函数图形表示。

当P点越过已知点C之后，误差继续增大，K值由4.8一直增大到无穷。当S =1700时，K=10.8。S=165。时，K=19.9。此后速度则迅速加快。P点从三角形中心点向危险圆移动时，在S=600β（P点在AB边的直线上）之前，K值变化缓慢，越过AB线后K值的变化不断加快，占- 800时，K80= 13.6。当P越过危险圆之后，误差开始减小，S=1o0时，K1oo =20.4；在S=112.80时，K有最小值，且Kn2= 14.06。当S继续增大，K值又迅速增大直至无穷。

由以上分析可知，在进行三点后方交会时，P点的位置选择非常关键应避免危险圆附近区域以及远离已知点的区域。

3.3 边角后方交会的分析

将收集到的数据按公式解算出误差结果，并绘制下表，如表1所示。

顾及到图像的匀称性以及操作的具体现场，采纳图2中的角度β为0?～180?，假设要求的边长S2为已知边的0-5倍；通过精度公式（β，S2，m），求得它们之间的关系，再以交会的角度β来作为纵轴，边长S2来作为横轴，并画出误差等值线图，由图形可以由如下分析。

1）当边长S2的长度在低于已知边的长度6倍时候，其角度β无论在什么范围变动的时候，待定点P的中误差的最大值都没有超出120mm。

当角度β在0?～20?、60?～120?、160?～180?的范围内的时候。未知点的点位误差相对较小，并且与已知边的边长S2，大小没有多大联系。

当边长S2是O～5倍的已知边的长度时，角度B无论怎样变化，未知点的误差总是不超过±60mm。

当角度β在40。左右，边长S2超过已知边的边长大约4倍的时候，未知点误差相对较大；当角度β在132?左右，边长S2超过已知边的边长大约4倍的时候，未知点误差相对较大。角度误差等值曲线图中，相对集中的两个空间内突现了较高的未知点的误差。

4 结论

通过后方交会测量精度影响，所得到的主要结论如下。

1）在角度后方交会的测量中（三点后方交会），角度对其影响较大，其角度在30?～60?之间，未知点点位误差较小；此外还与已知点的位置有一定的关系，当图形对称时精度较高。

2）在测边后方交会测量中，可以看出，当边长为已知的时候，其交会角y在90?～ll0?附近时候，未知点点位误差较小；当角度一定时候，边长选择尽量选取短边：