基于双重离散小波变换的遥感图像去噪算法
2015-12-25张倩
张倩
(河南经贸职业学院信息管理系,郑州 450018)
0 引言
在遥感图像获取、传输、存储以及解码等环节中不可避免地会混入一定程度的噪声,这些噪声对图像匹配、解译及目标提取等工作造成了严重影响。近年来,对于遥感图像的噪声滤除大体上有2类思路:①空间域去噪(de-noising),代表性的方法有偏微分方程方法[1-2]和字典学习算法[3];②变换域去噪,代表性的方法有离散小波变换(discrete wavelet transform,DWT)[4-5]、非二次采样轮廓波变换(non subsampled contourlet transform,NSCT)[6]、经验模态分解 (empirical mode decomposition,EMD)[7]等。其中,变换域去噪是目前遥感图像滤波的主流方法,但该类方法仅将图像进行多尺度分解,对各类子图像统一进行去噪,较少地顾及图像信息的连续性。受上述研究成果启发,本文对具有高斯白噪声和椒盐噪声的遥感图像进行2次离散小波变换,对变换后的各小波子图像分别采用改进的二维多级中值滤波(two-dimensionalmulti-stage median filtering,TMMF)算法和改进的小波硬阈值函数模型进行处理,通过二次小波重构获得去噪后的图像。
1 DWT原理
设函数Ø(t)为一可积函数,对其进行傅里叶变换获得函数(t),且满足[8]
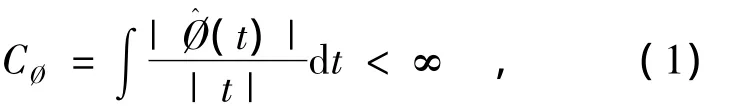
则称Ø(t)为小波母函数,并认为式(1)是小波函数可容许性条件。采用尺度因子a和平移因子b对Ø(t)进行伸缩和平移计算,得到函数Øa,b(t),即

对式(2)中的a和b进行离散化处理,即
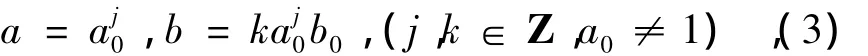
离散小波函数Øj,k(t)可定义为
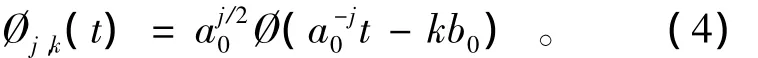
对于任意函数φ(t),对其进行离散小波变换后得到的各小波分解系数可描述为
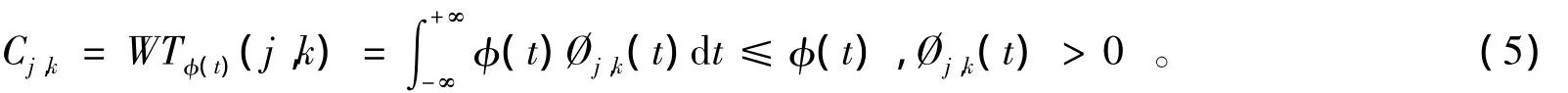
式(5)表示积分后的结果中包含2类函数。相应地,小波分解系数的重构形式为

2 TMMF及其改进算法
2.1 TMMF 算法
TMMF算法[9]通过将噪声点的一定邻域划分成4个不同方向的滤波模板(图1),分别进行中值滤波;然后将各模板的滤波结果进行适当计算,获得噪声点的滤波值。

图1 4个方向的滤波模板Fig.1 Filtering temp lates in four directions
对于图像中处于(i,j)处的噪声点,邻域大小为(2N+1)×(2N+1)(N为正整数)。采用TMMF算法滤波的过程为

式中:ax(i,j)(x=1,2,3,4)为4 个滤波模板的滤波值;Med[·]为中值滤波运算;A(i,j)为图像一定区域内的灰度矩阵。对集合{ax(i,j)}分别进行

计算,因此,对于(i,j)处的噪声点,其滤波值为

2.2 改进的TMMF算法
TMMF算法的不足之处在于:①遥感图像中尽管存在一些噪声,但从总体来说受到噪声污染的像素点所占比例很小,若对所有像素点进行滤波,会极大地增加算法的耗时;②该算法将图像中的目标信息大致分为水平(0°)、垂直(90°)、对角 45°和对角135°这4个方向,尽管对于经典中值滤波算法来说有效地刻画了图像中目标信息的方向性,但对于遥感图像来说,河流、道路、建筑物边缘等连续性信息的分布是杂乱无章的,若将这些信息的方向仅抽象为上述4个方向,显然是不太合理的;③该算法最终的滤波结果大致有2类情形,即待滤波点的灰度值要么保持不变,要么被上述4个滤波模板的滤波值替换。对于遥感图像而言,这容易导致图像中的河流、道路、建筑物边缘等部分信息出现“错位”或“移位”,且图像中的一些特征点(如建筑物“边角”、“道路拐点”等)信息丢失,就会增加后续的目标配准和图像解译的难度。
2.2.1 噪声判断准则和标记方法
对于噪声的检测方法,目前已发表了大量研究成果,主流方法是通过采用一定大小的检测模板在图像中按照行列顺序进行滑动,并按照如下准则进行噪声检测[10-11]:
1)极值检测法的判断准则为

式中f(x,y)为图像中任意一像素点的灰度值。
2)最值检测法的判断准则为

式中:f(x,y)为遥感图像中任意一像素点的灰度值;fmax(x,y),fmin(x,y)分别为噪声检测模板中的灰度最大、最小值。
上述2种方法基本上是假设图像中仅含有椒盐噪声的情形(即将图像中的极黑点或者极白点当作噪声)。而事实上,遥感图像中不仅只含有椒盐噪声,因此,本文采用5像素×5像素的方形检测窗口,对式(11)定义的检测方法进行适当改进,即
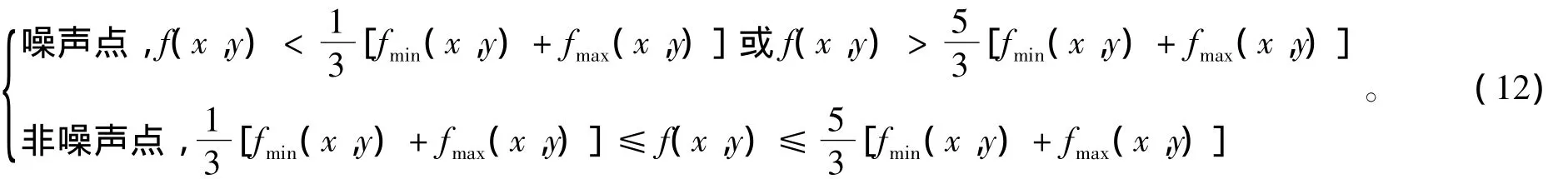
式(12)所定义的噪声检测方法能够将模板中的灰度值较低和较高的2部分像素点认定为噪声点并标记为“1”,而其余像素点则标记为“0”,因而随着检测模板在图像中的滑动,整景图像中的像素点被“二值化”,从而减少了滤波的盲目性。
2.2.2 新型滤波模板的设计
由式(7)可知,TMMF算法采用4个方向滤波模板实现对噪声点的滤除,这对于细节信息较少的一般数字图像而言比较实用。但遥感图像中大量的目标信息如河流、道路、建筑物边缘等呈多方向性分布,仅将它们的分布方向抽象成4种方向(0°,45°,90°,135°)显然是不够的。因此,本文又设计了另外4类新型滤波模板(图2),以对传统滤波模板进行必要的补充。
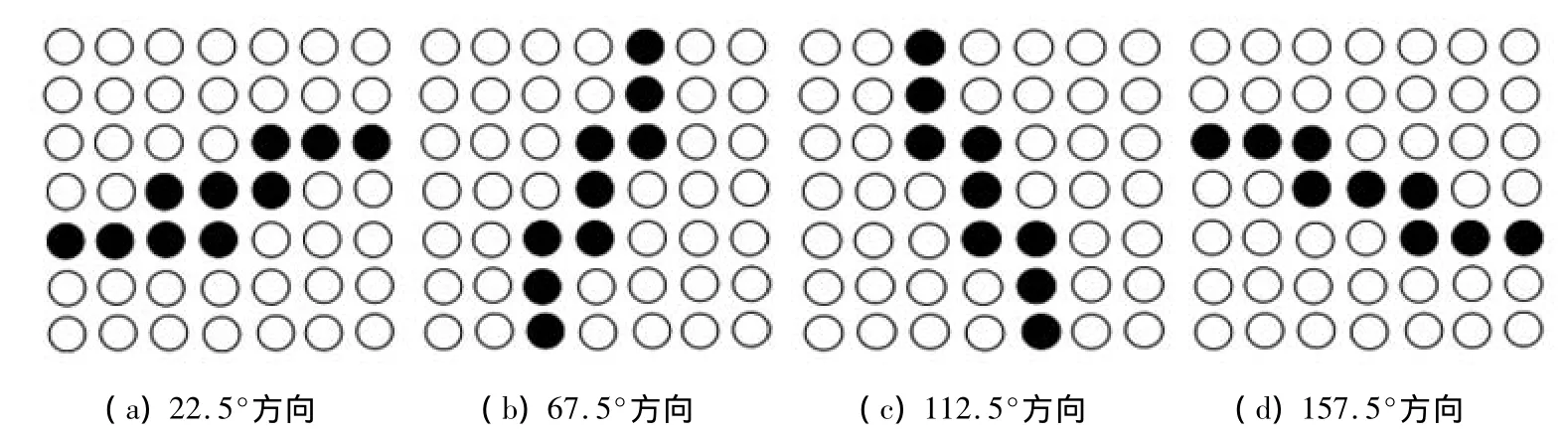
图2 4个新型的滤波模板Fig.2 Four new filtering tem p lates
图1和图2中的滤波模板组成了改进算法中的多方向滤波模板,提高了地物细节的保持能力。
2.2.3 加权滤波
对噪声点分别采用图1和图2的模板进行滤波,按照式(8)的运算思路获得如下滤波值集合,即
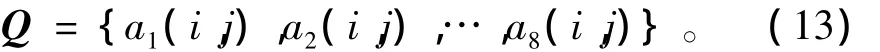
求取式(13)集合中的最大值amax(i,j)和最小值amin(i,j),并将集合Q中所有的值从大到小排列,取位于中间位置的2个值amed1(i,j)和amed2(i,j)以及噪声点灰度值f(i,j)组成集合,即
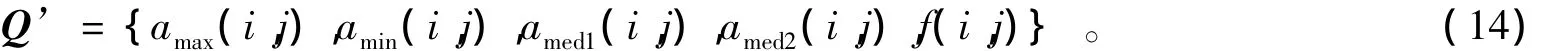
集合Q’中的前4个数值实质上就是噪声点一定邻域内的4个像素点,若采用式(9)的滤波方法(即采用它们其中的任意一值替换噪声点的灰度值),则无法充分顾及噪声点与该4个像素点的相关性。因此,本文通过设置一定的权重值,通过对集合Q’中前4个值进行加权求和,从而实现对噪声点灰度值的修正(而非简单地替换),以保持图像中目标信息的连续性。于是,最终的滤波结果为

式中:权重Px(x=1,2,3,4)为集合 Q’中前4个值对应的像素点与噪声点的几何距离。
3 实验及分析
3.1 算法的执行步骤
1)对含有噪声的遥感图像执行单层DWT,获得代表图像背景信息的低频子图像和代表图像中高频信息的高频子图像。
2)由于图像中的噪声经DWT后基本集中于高频子图像中,因此,对低频子图像可不作处理;对高频子图像再次执行单层DWT,获得次高频子图像和次低频子图像。
3)对次高频子图像,首先采用式(12)定义的噪声检测方法检测图像中的噪声并加以标记,然后对标记后的噪声点采用图1和图2所定义的多方向滤波模板、按照式(7)及式(13)—(15)定义的方法进行改进的二维多级加权中值滤波。
4)对次低频子图像,考虑到高频子图像中的噪声点随着小波分解层数的增加呈现迅速衰减的特征,采用对经典硬阈值去噪算法加以改进后的算法进行噪声抑制处理,得到

5)对步骤3)和步骤4)去噪后的小波子图像进行系数重构,最终获得去噪后的遥感图像。
3.2 实验结果及分析
分别对TMMF算法(算法1)及其改进算法[9](算法2)、小波阈值去噪算法[12](算法3)和本文算法(算法4)进行MATLAB编程实现。实验数据为3景含有混合噪声且细节信息较为丰富的图像以及1景存在一定程度失真的图像(分别记为图像1—图像4)。图像1—图像3的测试结果分别如图3—图5和表1所示;图像4的测试结果如图6所示。

图3 图像1不同算法的滤波结果Fig.3 Filtering results using different algorithms for image1

图4 图像2不同算法的滤波结果Fig.4 Filtering results using different algorithm s for image2
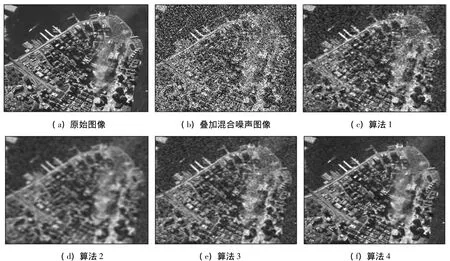
图5 图像3不同算法的滤波结果Fig.5 Filtering results using different algorithm s for image3
叠加了均值为0、方差为0.04的高斯白噪声以及密度达20%的椒盐噪声的3景遥感图像分别如图3(b)、图4(b)和图5(b)所示。①采用算法1分别对噪声图像进行去噪,图3(c)中公路中间白色线条、图4(c)中故宫护城河的边缘以及图5(c)右上角云层遮盖下的陆地边缘等连续性信息基本丧失,这是由于经典TMMF算法的最终滤波值来源于噪声点一定邻域内某像素点的灰度值的缘故。②算法2在滤波过程中分别赋予一定的权重,从而对滤波结果进行一定的修正,但图像整体上较为模糊,视觉效果较差(图3(d)、图4(d)和图5(d))。这是因为,算法2中的权重值的确定较为随机,并未充分考虑到图像中像素点间的高度相关性,这不仅不能有效地去除噪声,反而导致大量非噪声点的灰度值也被“修正”了。③算法3对图像中含有混合噪声的情况,首先采用中值滤波算法进行预处理,然后对滤波后的图像进行小波阈值去噪,处理结果分别如图3(e)、图4(e)和图5(e)所示。相对而言,算法3去噪效果优于算法1和算法2。这主要是因为算法3对图像中的混合噪声采取了逐级滤除的策略。④算法4的去噪结果如图3(f)、图4(f)和图5(f)所示,去噪后图像的清晰度明显优于其他几种算法。这主要得益于:①将噪声图像从空间域变换到小波域,仅对噪声集中的高频子图像进行处理,从而使得大部分背景信息得以保留;②通过对噪声进行预先检测和标记,提高了滤波的针对性,噪声点的滤波值是通过一定邻域的像素点灰度值加权求和得到的。
表1列出对图像1—图像3的峰值信噪比(peak signal to noise ratio,PSNR)和边缘保持指数(edge preserving index,EPI)的评价结果。
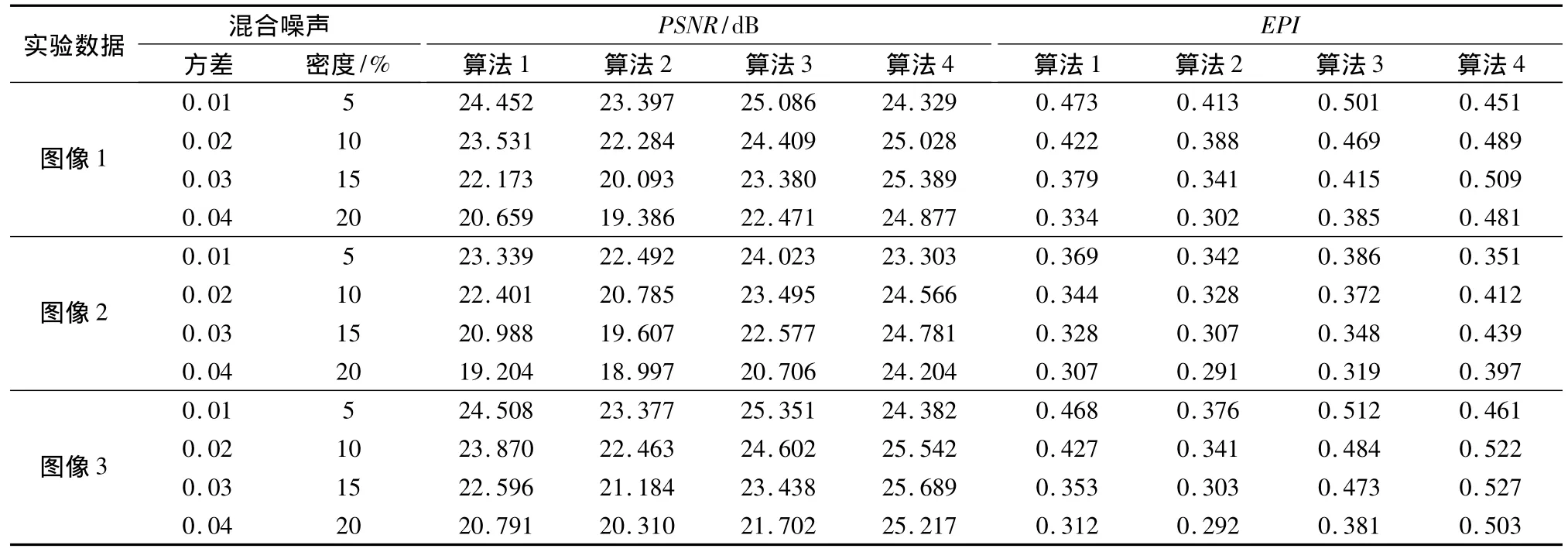
表 1 PSNR[12]与 EPI[13]评价结果Tab.1 Evaluation results of PSNR[12] and EPI[13]
从表1可以看出,算法4对于混合噪声强度较低(均值为0,方差为0.01,密度为5%的椒盐噪声所组成的混合噪声污染)图像的去噪效果不如算法3,这是因为,算法4中尽管对图像中的噪声进行了预先检测,但难免出现漏检或者误检的现象,将一些图像信息点误判为噪声点;而随着混合噪声强度的提高,算法4在噪声检测环节中的作用得以体现,绝大部分噪声被预先检测出来,从整体上看,算法4对应的PSNR值与EPI值高于其他3类算法。
图6(a)为一景四川玉树地震灾区的航空遥感图像,图像获取时由于受到震区气象条件的影响,导致获取的图像存在一定程度的失真。从图6可以看出,算法1—算法3对该图像的滤波处理收效甚微;而算法4基本实现了对图6(a)的有效滤波,说明算法4的滤波性能相对于其他3种算法而言,具有一定的优势。

图6 图像4不同算法的滤波结果Fig.6 Filtering results using different algorithms for image4
4 结论
针对含有噪声的遥感图像,提出了一种基于双重离散小波变换的去噪算法。该算法通过对噪声图像先后执行2次离散小波变换(DWT),仅对其中的次高频子图像和次低频子图像分别采用改进二维多级中值滤波(TMMF)算法和改进小波硬阈值去噪模型进行噪声抑制。理论分析和实验结果证明了该算法的有效性。
[1] 张九星,黑保琴,李盛阳,等.基于变分方法的遥感图像去噪研究[J].遥感技术与应用,2010,25(4):560-566.Zhang JX,Hei B Q,Li SY,et al.Remote sensing image noise removal research based on variational method[J].Remote Sensing Technology and Application,2010,25(4):560-566.
[2] 王相海,李 放,宋传鸣.局部自适应混合模型的遥感图像去噪算法[J].中国图象图形学报,2011,16(7):1289-1296.Wang X H,Li F,Song C M.Remote sensing image de-noising based on local adaptive mixture model[J].Journal of Image and Graphics,2011,16(7):1289-1296.
[3] 秦振涛,杨武年,潘佩芬.基于稀疏表示和自适应字典学习的“高分一号”遥感图像去噪[J].光电工程,2013,40(9):16-21.Qin Z T,Yang W N,Pan P F.The remote sensing image denoising of“the first satellite of high resolution”based on representation and dictionary learning[J].Opto-Electronic Engineering,2013,40(9):16-21.
[4] 余岸竹,姜 挺,唐志华,等.一种基于压缩感知的遥感影像混合去噪模型[J].测绘科学技术学报,2013,30(1):68-72.Yu A Z,Jiang T,Tang Z H,et al.A hybrid model for de-noising remote sensing image based on compressive sensing theory[J].Journal of Geomatics Science and Technology,2013,30(1):68-72.
[5] 王晓甜,石光明,牛 毅,等.基于移不变全方向角提升的遥感图像降噪[J].测绘学报,2011,40(5):555-562.Wang X T,Shi G M,Niu Y,et al.Translation invariant omnidirectional lifting based on remote sensing image denoising[J].Acia Geodaelica et Carlographica Sinica,2011,40(5):555-562.
[6] 李殿均,贾振红,覃锡忠,等.基于NSCT阈值萎缩法的遥感图像去噪[J].计算机工程,2012,38(5):227-229.Li D J,Jia Z H,Qin X Z,et al.Remote sensing image denoising based on NSCT threshold shrinkage approach[J].Computer Engineering,2012,38(5):227-229.
[7] 黄长均,郭际明,喻小东,等.干涉图EMD-自适应滤波去噪法[J].测绘学报,2013,42(5):707-714.Huang C J,Guo JM,Yu X D,et al.The study of interferogram de-noisingmethod based on EMD and adaptive filter[J].Acta Geodaetica Carlographica Sinica,2013,42(5):707-714.
[8] 程德强.矿井数字视频信息处理技术[M].北京:科学出版社,2012.Cheng D Q.Mine Digital Video Information Processing Technology[M].Beijing:Science Press,2012.
[9] 王明常,邢立新,杨毅恒,等.动态方向加权二维多级中值滤波的图像处理[J].吉林大学学报:信息科学版,2006,24(1):18-21.Wang M C,Xing L X,Yang Y H,et al.Directionalweighted two-dimensionalmulti-step median filtering in image processing[J].Journal of Jilin University:Information Science Edition,2006,24(1):18-21.
[10] 郑江云,陈春霞.应用中值滤波法消除高密度椒盐噪声算法[J].安庆师范学院学报:自然科学版,2013,19(4):55-58.Zheng JY,Chen CX.An algorithm for removal of high density salt and pepper noise based on median filtering[J].Journal of Anqing Teachers College:Natural Science Edition,2013,19(4):55-58.
[11] 张辰锐,樊养余,刘 姝,等.一种基于模糊决策的开关矢量中值滤波方法[J].计算机应用研究,2013,30(12):3870-3873.Zhang C R,Fan Y Y,Liu S,et al.Switching vector median filter based on fuzzy decision[J].Application Research of Computers,2013,30(12):3870-3873.
[12] 王小兵,孙久运,汤海燕.基于小波变换的图像混合噪声自适应滤波算法[J].微电子学与计算机,2012,29(6):91-95.Wang X B,Sun J Y,Tang H Y.Adaptive filtering algorithm for mixed noise image based on wavelet transform[J].Microelectronics and Computer,2012,29(6):91-95.
[13] 杨婧玮,李 贺,王智超.改进Frost算子在SAR图像斑点噪声抑制中的应用[J].测绘科学技术学报,2009,26(4):280-282.Yang JW,Li H,Wang ZC.Application of SAR image de-specklingmethod based on improved Frost filter[J].Journal of Geomatics Science and Technology,2009,26(4):280-282.
