利用交叉验证的小麦LAI反演模型研究
2015-12-25陈怀亮王连喜
任 哲,陈怀亮,王连喜,李 颖,李 琪
(1.南京信息工程大学江苏省大气环境监测与污染控制高技术研究重点实验室,南京 210044;2.南京信息工程大学环境科学与工程学院,南京 210044;3.中国气象局河南省农业气象保障与应用技术重点实验室,郑州 450003)
0 引言
叶面积指数(leaf area index,LAI)是表征植被冠层结构的关键参数,也是植被系统的一个重要参数。LAI能够对植被的冠层结构赋予直接的量化指标[1],获取准确的LAI数据对提高作物长势监测和产量预测精度具有重要价值[2]。LAI的反演研究在遥感技术发展早期就受到了重视,也一直是遥感反演领域的热点和难点之一。Bunnik[3]证实了利用遥感技术提取植被LAI的可能性,为LAI的反演奠定了基础;而高光谱遥感技术的兴起则大大加快了遥感反演技术从定性到定量发展的步伐[4]。对LAI的反演方法主要有物理模型法和经验模型法[5-6]。物理模型法用以物理方法为基础的植被冠层反射率模型进行LAI反演[7],能建立植被生理生化参数与冠层反射率的联系,但模型的解并不唯一[8];经验模型法则是指建立LAI与植被特征之间的回归模型,但模型受限于饱和效应[9]。
高光谱遥感数据具有波段窄且数量多的特点,相比多光谱数据,与LAI具有更高的相关性[10]。研究者们通常利用高光谱数据的特性确定敏感参数,建立LAI经验模型。农业遥感中,利用高光谱数据及其建立的植被指数能准确地反映出作物本身的光谱特征,并更方便地获取农学信息[11]。目前,高光谱的导数光谱技术(differential spectroscopy)及红边参数也越来越多地被用于反演 LAI[12]。利用实测光谱模拟MODIS等效反射率,构建植被指数及其与小麦LAI之间的经验模型[13],可为利用遥感技术进行大面积作物信息提取提供重要手段[14]。王秀珍等[15]通过水稻高光谱数据的各种变换形式表明,以红边面积和蓝边面积为变量的模型与水稻LAI关系密切。当前的研究主要针对LAI与高光谱数据之间的关系,反演LAI时未能充分考虑因样本数量的局限性及产生的随机误差会引起LAI经验模型中敏感参数和模型类型不同的问题。然而,通过更精确的统计学方法可以更精细地确定敏感参数以建立LAI经验模型。本文利用小麦高光谱数据、高光谱导数数据、植被指数及三边变量参数等数据,通过交叉验证建立小麦LAI的反演模型,并利用交叉验证后反演模型的决定系数(R2)和均方根误差(RMSE)判断反演结果的拟合效果。研究结果表明:交叉验证法可提高对小麦LAI反演结果的评判精度,更准确地提取反演小麦LAI的敏感参数及模型类型,并建立小麦LAI遥感反演的最优模型。
1 研究方法
1.1 试验方法
小麦高光谱数据及LAI采集试验于2014年3—5月间在河南省郑州市农业气象试验站(E 113°39',N 34°42')进行,涵盖拔节期、孕穗期、抽穗期和乳熟期等不同生育期中不同长势的小麦。试验区年平均气温14.3℃,年平均降雨量632 mm,土壤类型为砂壤土,小麦品种为郑麦366。
试验选择晴朗无云的天气,测量时间在10:00~12:00和14:00~15:00之间。本次试验选择长势具有代表性的小麦,取0.6 m×0.6 m的样方,使用冠层分析仪在垄间测定小麦的LAI值,并采集该范围内的小麦高光谱数据。样方内小麦长势均等,垄间距离相对均匀。将经过多次测量后的平均值作为该样方内小麦的光谱反射值和LAI值,以消除仪器所带来的随机噪声。
测量小麦高光谱数据的光谱仪是美国SVA公司生产的GER 1500便携式野外光谱测定仪,其光谱范围为350~1 050 nm,拥有512个通道,光谱采样间隔为1.5 nm,光谱分辨率为3 nm。每次采集数据前均用参照板对该光谱仪进行校正,以消除环境变化给采集数据带来的影响。测量小麦LAI数据的仪器是美国LI-COR公司生产的LAI-2000植物冠层分析仪,其使用320~490 nm的感应波段,通过“鱼眼”镜头感应天空被遮蔽的情况,进而得到太阳辐射的透过率。根据LAI-2000对测量天气(在阴天等散射光条件下进行观测)的要求,测量时在“鱼眼”镜头上使用了270%的遮光盖以减少阳光直射的影响,且尽可能在太阳被云遮挡的时候进行测量。测量时,光谱仪与冠层分析仪的镜头都水平朝向天空,且不被测量者身影遮挡阳光,以免测量者被计入LAI值内,而且测量者都穿着深色不反光的衣物。
1.2 数据处理
本次试验采集到81组有效的小麦高光谱及对应的 LAI数据,LAI的平均值为 4.65,最大值为7.85,最小值为1.09。计算出小麦高光谱数据样本的一阶和二阶导数光谱(对高光谱数据进行求导能在一定程度上削弱土壤背景的影响),用于进行逐步回归分析和对小麦LAI进行反演。由于高光谱数据存在着采样间隔的离散型,故导数光谱需用差分法来近似计算[16],即
一阶导数光谱为

二阶导数光谱为
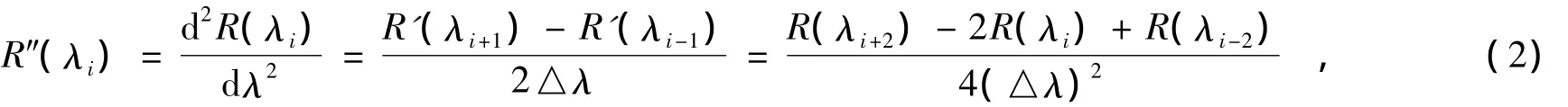
式中:λi为波段i的波长;R(λi)为波长λi处的光谱反射率;△λ为波长λi-1到λi的差值。采用导数光谱可以消除部分背景和大气散射光谱对目标光谱的影响。
为了减小样本的随机性给反演效果带来的误差,本文通过交叉验证进行模型选择。为了对模型进行验证,本文选用了2014年4月初—5月底山东省1 km空间分辨率的MODIS-L1B和MODIS-LAI数据,利用ENVI软件进行几何纠正及裁剪等预处理。在利用小麦高光谱数据构建表1中的各植被指数时,分别选用与MODIS传感器通道对应的蓝光波段(459~479 nm)、红光波段(620~670 nm)及近红外波段(841~876 nm)高光谱实测数据,模拟MODIS传感器通道进行大面积应用。

表1 研究中采用的植被指数Tab.1 Vegetation indices used in this study
利用小麦高光谱数据构建的各类常见植被指数(表 1)和三边变量参数(表 2)[15,22-23],能够很好地反映出小麦在各生育期中的植被特征。

表2 研究中采用的三边变量参数Tab.2 Trilateral variable parameters in this study
1.3 交叉验证法
交叉验证法主要用于选择模型,在统计学上是将数据样本切割为小子集,通过对各子集之间的分析与验证确立模型类型[24]。该方法不需要任何前提便可直接估计误差,具有应用普遍性和操作简便性,是一种行之有效的模型选择方法;特别是在数据量不足的情况下,数据的重复利用能在模型选择方面显示出更多的优越性[25]。交叉验证法分为保留交叉验证(hold-out)、留P交叉验证和K折交叉验证。本文使用的是9折交叉验证法。验证的基本过程为:将高光谱数据及导数光谱数据平均分为9组,轮流选取其中8组数据作为训练集,使用统计产品与服务解决方案(statistical product and service solutions,SPSS)软件进行逐步回归分析,建立LAI反演模型;利用剩余的1组数据作为验证集,进行拟合精度检验。如上所述共重复进行9次回归分析及精度检验,最后对9次精度检验的决定系数和均方根误差进行平均,来检验小麦LAI反演模型的拟合效果。所有小麦LAI数据的方差为2.81;在对数据进行分组之后,9组LAI数据的平均方差为2.73。
2 结果与分析
2.1 相关性分析
图1示出小麦高光谱数据与LAI数据的相关关系。
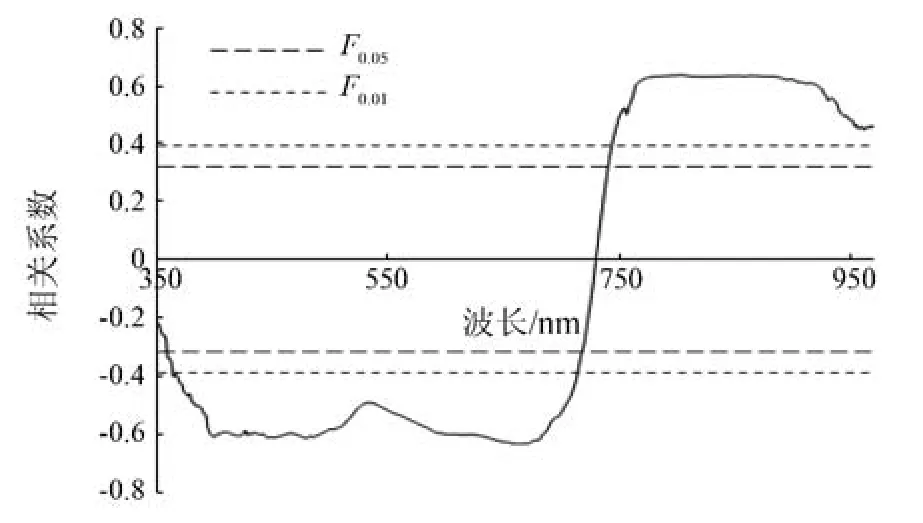
图1 小麦高光谱数据与LAI的相关关系Fig.1 Correlation between hyperspectral data and LAI of wheat
从图1可以看出,当波长小于728 nm时,小麦高光谱数据与LAI呈负相关关系,此区间内相关系数绝对值最大的为波长661 nm处的-0.634,且在该处形成了一个波谷;同时,在蓝光波段的光谱数据与小麦LAI也具有较高的相关性,形成了另一个波谷。相关系数在680 nm处开始迅速增大,在764 nm之后趋于平稳,并在802 nm处达到了最大值0.627。
对5个植被指数和6个三边变量参数与小麦LAI值进行相关性分析的结果(表3)表明,所有的参数与小麦LAI的相关性均通过了0.01的极显著性检验水平,表现出了极好的相关性。在植被指数与小麦LAI的相关分析中,RVI与小麦LAI的相关性最优(相关系数为0.905),其后依次为NDVI,MSAVI,EVI和DVI。而在三边变量参数与小麦LAI的相关分析中,相关性最好的为红边面积和蓝边面积的比值(Sred/Sblue),相关系数为0.840,但小于RVI和NDVI与小麦LAI的相关系数;而其归一化值[(Sred-Sblue)/(Sred+Sblue)]与小麦LAI的相关系数为0.833。其中,由于黄边面积Syellow为负值,因此,红边面积和黄边面积的比值(Sred/Syellow)及其归一化值[(Sred-Syellow)/(Sred+Syellow)]与小麦LAI呈负相关关系,且在所有参数与小麦LAI的相关性中表现不佳。

表3 植被指数、三边变量参数与小麦LAI的相关系数Tab.3 Correlation coefficient between vegetation indices,trilateral variable param eters and LAI of wheat
2.2 小麦LAI反演模型的效果比较
本文使用小麦高光谱数据、光谱导数数据、植被指数及三边变量参数等数据,利用交叉验证法对小麦LAI进行回归分析,其结果如表4所示。

表4 交叉验证法反演小麦LAI模型的拟合效果Tab.4 Im itative effect of wheat LAIm odel inversed by cross-validation
对小麦高光谱数据及其一阶和二阶导数光谱数据进行逐步回归交叉验证的结果表明,其反演模型的R2比植被指数和三边变量参数回归模型的R2大,在逐步回归模型中,被优先选入的波段多为近红外波段和红光波段等对绿色植被较为敏感的波段。从表4中还可以看出,经过交叉验证后,逐步回归模型的RMSE比植被指数和三边变量参数与小麦LAI回归模型的RMSE小。其中,小麦高光谱一阶导数数据对小麦LAI的逐步回归反演模型的R2达到了0.900,RMSE为0.589 3,是所有模型中拟合效果最好的;但因该逐步回归模型选入的波段数量较多以及需要采用导数计算方式,在实际应用中并不方便。
在5个植被指数对小麦LAI进行的非线性(对数、指数和立方)回归分析中,RVI和NDVI的3种回归模型的反演拟合效果明显优于其余3种植被指数反演模型,其R2较大,RMSE较小,可作为反演小麦LAI的敏感参数;其中,又以RVI的立方回归模型的拟合效果最佳(R2=0.848,RMSE=0.595 7)。其余3种植被指数(EVI,DVI和MSAVI)对小麦LAI回归模型的反演拟合效果较差,不适合用于对小麦LAI的反演。从表4可以看出,利用植被指数对小麦LAI进行非线性回归分析时,立方回归模型在整体上拟合效果优于对数回归模型和指数回归模型。
在利用三边变量参数对小麦LAI进行非线性回归分析中,其拟合效果与植被指数对小麦LAI回归分析的效果接近,其中最优的为Sred/Sblue的对数回归模型(R2=0.808,RMSE=0.648 2)。与植被指数对小麦LAI的非线性回归分析结果类似的是,利用三边变量参数对小麦LAI反演的结果中,立方回归模型在整体上拟合效果优于对数回归模型和指数回归模型。在对非线性回归的结果进行分析时可以发现,R2并不能决定该模型RMSE的大小;同时,R2也不能很好地反映出模型的估测精度。由于R2是模型估算值与真实值之间的曲线相关关系的反映[26],因此RMSE成为本次研究中更重要的判断指标。
2.3 基于敏感参数的小麦LAI反演模型
由表 4 可知,RVI,NDVI,Sred/Sblue和(Sred-Sblue)/(Sred+Sblue)在反演小麦LAI中都是较为敏感的参数,其中,RVI,NDVI,(Sred-Sblue)/(Sred+Sblue)立方回归模型以及Sred/Sblue对数回归模型对小麦LAI具有较好的拟合效果。利用小麦在所有生育期内的样本数据,通过上述4种模型对小麦LAI进行回归建模,得到的结果如图2所示。
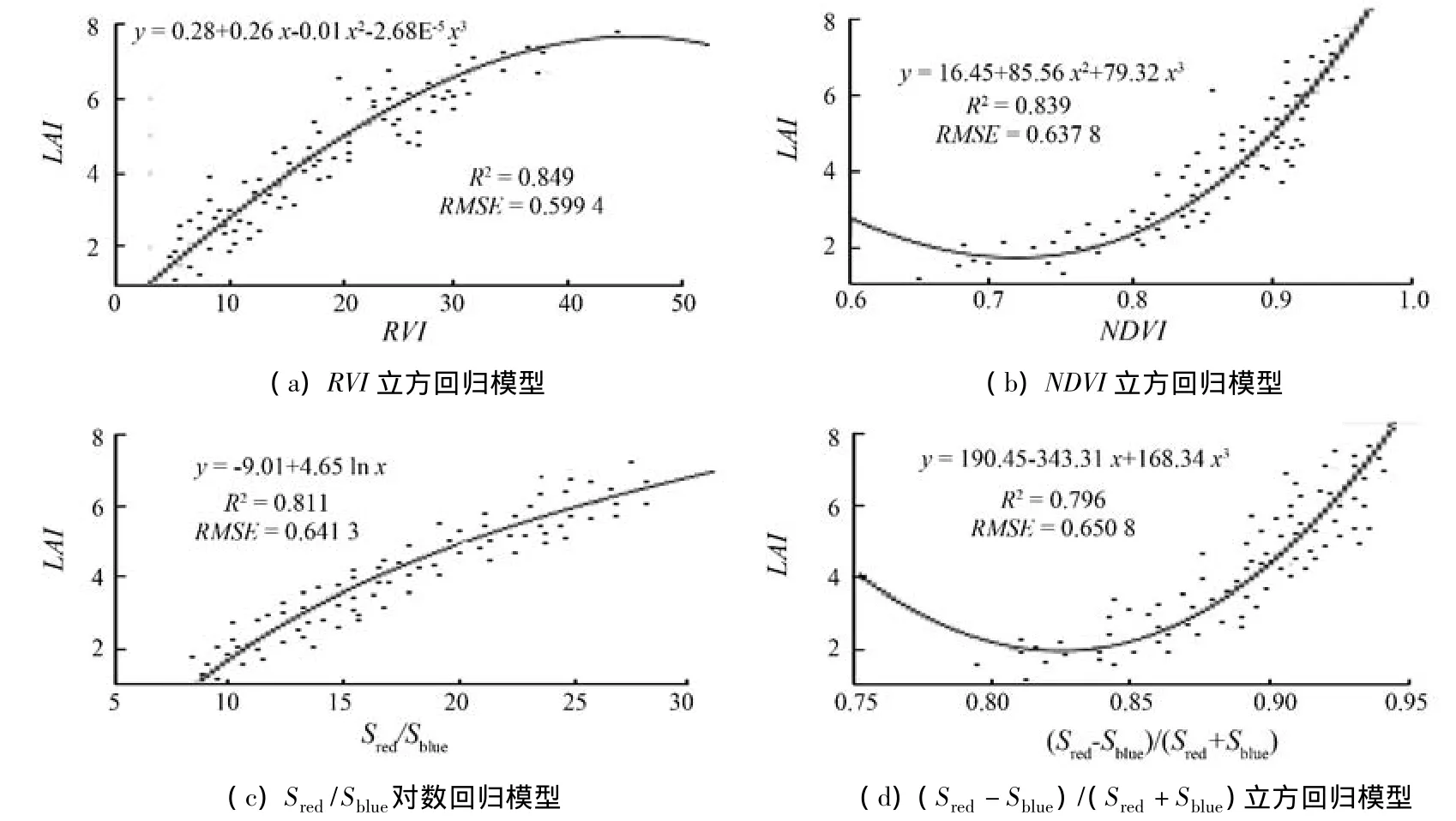
图2 基于不同敏感参数的小麦LAI反演模型Fig.2 Wheat LAI inversion model based on different sensitive parameters
通过精度分析可知,RVI立方回归模型、Sred/Sblue对数回归模型和(Sred-Sblue)/(Sred+Sblue)立方回归模型的R2比经过交叉验证的结果更大,但NDVI立方回归模型的R2比经交叉验证的结果减小了0.01。同时,与交叉验证后结果的RMSE值相比,NDVI立方回归模型、Sred/Sblue对数回归模型和(Sred-Sblue)/(Sred+Sblue)立方回归模型的RMSE值更小,但RVI立方回归模型的RMSE值增大了0.003 7。这4个模型当中,以RVI立方回归模型的拟合效果最优,其R2最大、RMSE最小。
利用所有样本的小麦高光谱数据及其一阶和二阶导数对小麦LAI进行逐步回归分析后可知,3个逐步回归模型的R2都有所增加,RMSE有所减小;但由于被选入的波段数量过多,且多为近红外与红光波段,故不便在实际工作中应用。虽然高光谱原始数据及其二阶导数的逐步回归模型的R2大于RVI立方回归模型的R2,但得到的RMSE却更大,拟合效果仍然不如RVI立方回归模型。
2.4 反演模型的验证
为了评价RVI立方回归模型对小麦LAI的反演效果,利用MODIS卫星遥感数据对其进行效果验证。验证中利用了覆盖山东省小麦种植区的MODIS-L1B及MODIS-LAI数据,利用MODIS-L1B的近红外和红光波段构建了NDVI时间序列,通过阈值法[27]提取山东省小麦种植区域,并运用这2个波段构建RVI立方回归模型以提取山东省各地区小麦LAI信息,与同期的MODIS-LAI数据进行比对。其中,对拔节期与孕穗期小麦反演得到的LAI值在整体上比同期MODIS-LAI的值偏大;而到了抽穗期与乳熟期,MODIS-LAI值在整体上比反演得到的小麦LAI值偏大。经过相关分析,反演得到的小麦 LAI值与MODIS-LAI值的相关系数为0.61,通过了0.01极显著性检验水平。验证结果表明,利用RVI立方模型进行小麦LAI的反演具有较好的效果。
3 结论
本文利用小麦高光谱数据,计算出其一阶和二阶导数数据,并构建植被指数及三边变量参数等数据;通过交叉验证法对小麦LAI进行回归分析,并对比各反演模型的拟合效果,得到以下结论:
1)利用高光谱原始数据及其一阶和二阶导数对小麦LAI进行逐步回归的拟合结果总体优于植被指数及三边变量参数构建的回归模型,其中又以一阶导数逐步回归模型的拟合效果最优;在利用敏感参数对小麦LAI进行反演时,RVI立方回归模型比其他模型的拟合效果更好。
2)在运用目前遥感技术对小麦LAI反演时,由于卫星传感器通道的限制,导致高光谱数据的导数无法完全获取。因此,RVI立方回归模型可认为是用于遥感数据反演小麦LAI的最优模型;且在利用空间分辨率更高的遥感数据时,会具有更好的相关性。随着高光谱遥感技术的发展,利用交叉验证确定敏感参数及模型类型将会进一步提高反演作物LAI的精确度。
3)经过对同一参数是否利用了交叉验证法进行回归分析的对比之后发现,各个参数对LAI反演结果中的RMSE值在交叉验证后总体上比未经交叉验证的RMSE值小,且决定系数R2比未进行交叉验证反演结果的值大。同时,在分组过程中选择不同的分组方法以及分组数量,会导致拟合效果的不同,但不影响交叉验证法在模型选择上的优越性,相信会有更好的交叉验证法用于选择小麦LAI的反演模型。
[1] Dobermann A,Pampolino M F.Indirect leaf area index measurement as a tool for characterizing rice growth at the field scale[J].Communications in Soil Science and Plant Analysis,1995,26(9/10):1507-1523.
[2] 黄敬峰,王 渊,王福民,等.油菜红边特征及其叶面积指数的高光谱估算模型[J].农业工程学报,2006,22(8):22-26.Huang JF,Wang Y,Wang FM,etal.Red edge characteristics and leaf area index estimation model using hyperspectral data for rape[J].Transactions of the CSAE,2006,22(8):22-26.
[3] Bunnik N J.The Multispectral Reflectance of Shortwave Radiation by Agricultural Crops in Relation with Their Morphological and Optical Properties[D].Wageningen:Meded.Candbouwhoge School,1978.
[4] 邢著荣,冯幼贵,李万明,等.高光谱遥感叶面积指数(LAI)反演研究现状[J].测绘科学,2010,35(s1):162-164,62.Xing Z R,Feng Y G,LiW M,et al.The research status of inversion of leaf area index with hyperspectral remote sensing[J].Science of Surveying and Mapping,2010,35(s1):162-164,62.
[5] Yang F,Sun JL,Fang H L,et al.Comparison of differentmethods for corn LAI estimation over northeastern China[J].International Journal of Applied Earth Observation and Geoinformation,2012,18:462-471.
[6] Darvishzadeh R,Atzberger C,Skidmore A,etal.Mapping grassland leaf area index with airborne hyperspectral imagery:A comparison study of statistical approaches and inversion of radiative transfer models[J].ISPRS Journal of Photogrammetry and Remote Sensing,2011,66(6):894-906.
[7] 杨贵军,赵春江,邢著荣,等.基于PROBA/CHRIS遥感数据和PROSAIL模型的春小麦LAI反演[J].农业工程学报,2011,27(10):88-94.Yang G J,Zhao C J,Xing ZR,et al.LAIinversion of springwheat based on PROBA/CHRIS hyperspectral Multi-angular data and PROSAILmode[J].Transactions of the CSAE,2011,27(10):88-94.
[8] Yang G J,Zhao C J,Liu Q,et al.Inversion of a radiative transfer model for estimating forest LAI from multisource and multiangular optical remote sensing data[J].IEEE Transactions on Geoscience and Remote Sensing,2011,49(3):988-1000.
[9] Schlerf M,Atzberger C.Inversion of a forest reflectance model to estimate structural canopy variables from hyperspectral remote sensing data[J].Remote Sensing of Environment,2006,100(3):281-294.
[10] 陈雪洋,蒙继华,朱建军,等.冬小麦叶面积指数的高光谱估算模型研究[J].测绘科学,2012,37(5):141-144.Chen X Y,Meng JH,Zhu JJ,et al.Hyperspectral estimationmodels for leaf area index ofwinterwheat[J].Science of Surveying and Mapping,2012,37(5):141-144.
[11] Nguyen H T,Lee BW.Assessment of rice leaf growth and nitrogen status by hyperspectral canopy reflectance and partial least square regression[J].European Journal of Agronomy,2006,24(4):349-356.
[12] MauserW,Bach H.Imaging Spectroscopy in Hydrology and Agriculture Determination of Model Parameters[M].Dordrecht,Netherlands:Kluwer Academic Publishing,1995:261-283.
[13] 刘东升,李淑敏.北京地区冬小麦冠层光谱数据与叶面积指数统计关系研究[J].国土资源遥感,2008,20(4):32-34,42.doi:10.6046/gtzyyg.2008.04.08.Liu D S,Li SM.Statistical relationship between LAI indices and canopy spectral data of winter wheat in Beijing area[J].Remote Sensing for Land and Resources,2008,20(4):32-34,42.doi:10.6046/gtzyyg.2008.04.08.
[14] 侯学会,牛 铮,黄 妮,等.小麦生物量和真实叶面积指数的高光谱遥感估算模型[J].国土资源遥感,2012,24(4):30-35.doi:10.6046/gtzyyg.2012.04.06.Hou X H,Niu Z,Huang N,et al.The hyperspectral remote sensing estimation models of total biomass and true LAIof wheat[J].Remote Sensing for Land and Resources,2012,24(4):30-35.doi:10.6046/gtzyyg.2012.04.06.
[15] 王秀珍,黄敬峰,李云梅,等.水稻叶面积指数的高光谱遥感估算模型[J].遥感学报,2004,8(1):81-88.Wang X Z,Huang JF,Li Y M,et al.The study on hyperspectral remote sensing estimation models about LAIof rice[J].Journal of Remote Sensing,2004,8(1):81-88.
[16] Tsai F,Philpot W.Derivative analysis of hyperspectral data[J].Remote Sensing of Environment,1998,66(1):41-51.
[17] Jordan C F.Derivation of leaf-area index from quality of light on the forest floor[J].Ecology,1969,50(4):663-666.
[18] Rouse JW,Haas R H,Schell JA,et al.Monitoring vegetation systems in the Great Plains with ERTS[C]//Proceedings of Third ERTSSymposium.Greenbelt:NASA SP-351,1973,1:309-317.
[19] Liu H Q,Huete A.A feedback based modification of the NDVI to minimize canopy background and atmospheric noise[J].IEEE Transactions on Geoscience and Remote Sensing,1995,33(2):457-465.
[20] Richardson A J,Wiegand C L.Distinguishing vegetation from soil background information[J].Photogrammetric Engineering and Remote Sensing,1977,43(12):1541-1552.
[21] Qi J,Chehbouni A,Huete A R,etal.AModified soil adjusted vegetation index[J].Remote Sensing of Environment,1994,48(2):119-126.
[22] 王秀珍,王人潮,黄敬峰.微分光谱遥感及其在水稻农学参数测定上的应用研究[J].农业工程学报,2002,18(1):9-13.Wang X Z,Wang R C,Huang JF.Derivative spectrum remote sensing and Its application inmeasurement of rice agronomic parameters of rice[J].Transactions of the CSAE,2002,18(1):9-13.
[23] 谭 倩,赵永超,童庆禧,等.植被光谱维特征提取模型[J].遥感信息,2001(1):14-18.Tan Q,Zhao Y C,Tong Q X,et al.Vegetation spectral feature extractionmodel[J].Remote Sensing Information,2001(1):14-18.
[24] Kohavi R.A study of cross-validation and bootstrap for accuracy estimation and model selection[J].Proceedings of the Fourteenth International Joint Conference on Artificial Intelligence,1995,2(12):1137-1143.
[25] 范永东.模型选择中的交叉验证方法综述[D].太原:山西大学,2013.Fan Y D.A Summary of Cross-Validation in Model Selection[D].Taiyuan:Shanxi University,2013.
[26] 陈 拉,黄敬峰,王秀珍.不同传感器的模拟植被指数对水稻叶面积指数的估测精度和敏感性分析[J].遥感学报,2008,12(1):143-151.Chen L,Huang JF,Wang X Z.Estimating accuraciesand sensitivity analysis of regression models fitted by simulated vegetation indicesof different sensors to rice LAI[J].Journal of Remote Sensing,2008,12(1):143-151.
[27] 权文婷,王 钊.冬小麦种植面积遥感提取方法研究[J].国土资源遥感,2013,25(4):8-15.doi:10.6046/gtzyyg.2013.04.02.Quan W T,Wang Z.Researches on the extraction of winter wheat planting area using remote sensingmethod[J].Remote Sensing for Land and Resources,2013,25(4):8-15.doi:10.6046/gtzyyg.2013.04.02.
