强度折减法与极限平衡法对比分析——以安康市一边坡为例

袁茂莲 赵天彪 巫正海 林 远

（1.西南石油大学地球科学与技术学院，四川 成都 610500；2.四川建筑职业技术学院交通与市政工程系，四川 德阳 618000；3.西南石油大学土木工程与建筑学院，四川 成都 610500）

0 引言

边坡稳定性分析是边坡设计的前提。然而这个问题至今仍未得到妥善解决，因为解决这一问题必须先要查清坡体的地质状况及其强度参数，同时又要有科学合理的分析方法[1]。对于均质土坡，可以通过各种优化方法来搜索危险滑动面；但是对于岩质边坡，由于实际岩体中含有大量不同构造、产状和特性的不连续结构面，传统极限平衡方法尚不能搜索出危险滑动面以及相应的稳定安全系数。而有限元强度折减法是通过不断降低边坡岩土体的抗剪切强度参数，使其达到极限破坏状态为止，从而得到边坡的强度储备安全系数，使边坡稳定分析进人了一个新的时代[2-4]。

1 有限元强度折减安全系数定义

边坡稳定性分析中，安全系数是评价边坡稳定性的一个重要指标。对于边坡安全系数的定义，在岩土工程历史中共经历了三次大的变化：第一次是采用的力矩定义[5]，第二次采用的是剪应力定义[6]，第三次采用的是抗剪强度折减定义[7-8]。其中，前两次定义都是基于极限平衡理论，而第三次关于抗剪强度折减的定义，其实质与用剪应力定义是一致的。但是，它为土坡稳定性分析的数值实施提供了理论依据，使得通过数值计算得到边坡的整体安全系数成为现实。

对于摩尔—库仑材料，抗剪强度折减安全系数可表示为:

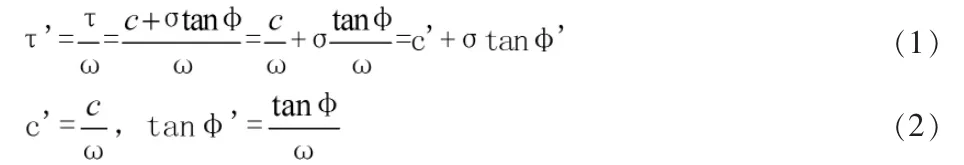
此强度折减形式的安全系数定义与边坡稳定分析的极限平衡条分法安全系数的定义形式是一致的。

2 强度折减理论中边坡失稳判据

有限元强度折减法分析边坡稳定性的一个关键问题是如何根据有限元计算结果来判别边坡是否处于破坏状态。目前的失稳判据主要有两类：

（1）在有限元计算过程中采用力和位移的不收敛作为边坡失稳的标志。

（2）以广义塑性应变或者等效塑性应变从坡脚到坡顶贯通作为边坡破坏的标志。

塑性区贯通并不一定意味着破坏，塑性区贯通是破坏的必要条件，但不是充分条件，还要看是否产生很大的且无限发展的塑性变形和位移，有限元计算中表现为塑性应变和位移产生突变[9]。

土体整体破坏的标志应是滑体出现无限移动，此时滑移面上的应变会出现突变。同时，有限元计算也会出现计算不收敛。由此可见，上述（1）（2）两种判据是一致的[10]。

3 屈服准则的选用

有限元强度折减法中岩土材料本构模型采用理想弹塑性模型，安全系数大小与采用的屈服准则密切相关，不同的准则会得出不同的安全系数。

本文采用ABAQUS6.10 对边坡稳定性进行数值计算，在ABAQUS软件中采用D-P 准则。该准则是在米赛斯准则的基础上，考虑平均压应力而将米赛斯条件推广成为如下公式:

式中，I1和J2分别为应力张量的第一不变量和应力偏张量的第二不变量，α 及k 是与岩土材料内摩擦角φ 和粘聚力c 有关的系数。

4 实例应用

湖景嘉苑小区位于安康市汉滨区瀛湖镇郭家店境内。以西为瀛湖镇街道；以东为永久性挡土墙和原修建安康水电站专用铁路线及民房；北为居民区；南为该小区正建2# 楼场地。整个场地东高西低。

4.1 岩性参数

根据勘探揭露，场地土层在勘探深度内岩土层主要为：粉质粘土和千枚岩，对应建立模型设置上层为弹塑性介质（土体），c 取24kPa，φ 取17°，γ 取19.6，泊松比0.3；下层为弹性介质（强风化千枚岩），c取10KPa，φ 取35°，γ 取23，泊松比0.25，弹性模量1.2 GPa。

4.2 稳定性系数计算

4.2.1 有限元强度折减法计算结果

本文以该边坡的工程地质勘察剖面为原型建立数值模型，采用ABAQUS6.10 数值模拟软件进行模拟。在数值模拟中，两层土体均采用理想线弹性模型，选取场变量FV1 自0.5-2.0，每间隔0.25 进行一次强度折减。建立的有限元网格模型以一个剖面为例，如图1。

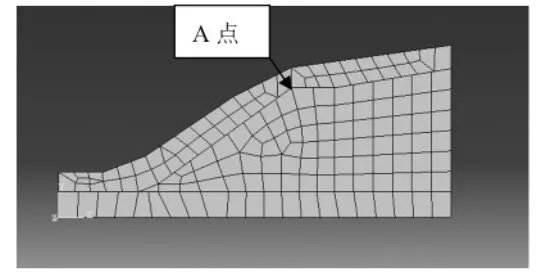
图1 边坡有限元网格模型

本文选择点A 作为场变量（FV1）和X 方向位移（U1）关系曲线的结点，利用ABAQUS 提供的Combine 函数，将FV1 随U1 的变化关系绘制出来，见图2。从图2 中可以看出，A 结点水平位移有一个明显的拐点，本文以拐点作为边坡不稳定的评价标准，则安全系数Fs=1.31。

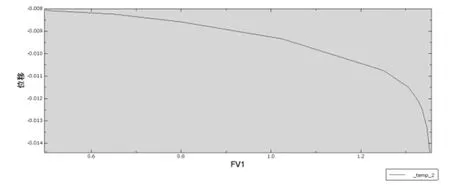
图2 场变量与X 方向位移关系曲线

图3 位移等值线云图

从图4 中，t=0.5689s 的PEMAG 图中清楚的表明了边坡失稳过程。即从一开始是A 点附近的表层土体出现屈服，并向下滑动，随后下侧土体挤压坡脚土体，导致坡脚土体发生塑性变形。

图4 积分点上的等效塑性应变

采用上述方法计算出其他剖面稳定性安全系数如表1：

表1 数值模拟稳定性计算结果

由数值计算结果可以看出：在天然状态下，勘察区内斜坡稳定系数Fs=1.25～1.59，说明在天然状态下斜坡处于稳定状态。

4.2.2 极限平衡法计算结果

勘察区斜坡荷载类型包括斜坡岩体自重静载荷和道路动载荷。本文主要目的是将有限元强度折减法与极限平衡法做对比，所以此处荷载工况仅考虑天然自重工况。

该区斜坡土质覆盖层较厚，根据《建筑边坡工程技术规范》（GB50330-2002）规范，采用复杂土层折线性计算公式对斜坡进行验算。根据《滑坡防治工程勘查规范》(DZ/T0218-2006)，安全稳定性系数fst 取1.15，计算结果见表2。

表2 斜坡稳定性计算结果

由计算结果可以看出：在天然状态下，勘察区内斜坡稳定系数Fs=1.239～1.578，说明在天然状态下斜坡处于稳定状态。

4.3 对比分析

通过对比以上两种计算结果，可以发现，强度折减法与极限平衡法相比总体都偏于不保守，其相对误差为0.31-5.28%，在工程允许范围内，也说明有限元强度折减法在求解边坡稳定性系数上是可行的。

5 结论

通过本文以一边坡工程实例，将有限元强度折减法与传统的极限平衡法计算边坡稳定性系数并进行比较，可以得出如下结论：

（1）有限元强度折减法计算的边坡稳定性系数与传统极限平衡法计算结果较为接近，可以作为工程参考；

（2）极限平衡法计算结果较有限元强度折减法更为保守；

（3）数值模拟边坡变形破坏结果更为形象直观，但也存在滑动面不清晰的缺陷。

［1］陈祖煜.土质边坡稳定分析:原理、方法、程序[M].北京:水利水电出版社，2003.

［2］Griffiths D V，Lane P A.Slope stability analysis by finite elements[J].Geotechnique，1999，49(3):387-403.

［3］Dawson E M，Roth W H，Drescher A.Slope stability analysis by strength reduction[J].Geotechnique，1999，49(6):835-840.

［4］宋二祥，高翔，邱玥.基坑土钉支护安全系数的强度参数折减有限元法[J].岩土工程学报，2005，27(3):258-263.

［5］Fellinius W.Calculation of stability of earth dams[C]//Trans 2ndinternational congress of large dams，1936(4):445.

［6］Bishop A W.The use of the slip circle in the stability analysis of slopes[J].Geotechnique，1955(5):7-17.

［7］Duncan J M.State of the art:limit equilibrium and finite element analysis of Slope[J].Journal of Geotechnical Engineering，ASCE，1996，122(7):577-595.

［8］Zienkiewicz O C，Humpheson C and Lewis R W.Associated and non-associated visco-plasticity and plasticity in soil mechanics[J].Geotechnique，1975，25(4):671-689.

［9］郑颖人，赵尚毅.有限元强度折减法在土坡与岩坡中的应用[J].岩石力学与工程学报，2004，23(19):3381-3388.

［10］郑颖人，赵尚毅，宋雅坤.有限元强度折减法研究进展[J].后勤工程学院学报，2005，3:1-6.