钢筋混凝土预制板动力特性试验研究

孟庆峰 朱东新 莫静琳 刘 东 晏金山

（1. 中国水电顾问集团中南勘测设计研究院有限公司 长沙市 410014；2. 湖南省水利水电勘测设计研究总院 长沙市 410007；3. 湖南省高速公路管理局湘西管理处 吉首市416000；4.湖南省交通规划勘察设计院 长沙市 410008）

结构动力特性一般包括结构自振频率、振型及阻尼等。它是结构所固有的特性，能准确反映出结构的整体力学性能[1～3]。而对于工程结构，容易实现和测量的恰是结构动力响应。利用结构的动力响应识别结构的模态参数和物理参数[4]，进而评价结构性能、判别结构损伤的方法即为结构动力试验检测技术。结构动力检测方法可不受结构规模和隐蔽部位的限制，只要在可接触到的结构部位安装动力响应传感器即可[5]。本文通过结构动力检测技术测试分析了一根从服役30年的房屋结构上拆除下来的一块预制板的结构动力学特性（自振频率、振型及阻尼），通过试验结果判明了其总体结构刚度和内在力学性能。

1 预制板动力特性测试与分析

1.1 试验基本情况

试验测试构件为某房屋结构预制板，板长340 cm，宽46 cm，厚12 cm，板内有预留直径为7.5 cm的圆形孔洞4 个，等间距布置。

通过模态试验分析该预制板结构的动力学特性（自振频率、振型及阻尼）、判断其总体结构刚度和内在力学特性[6]。试验主要内容包括：结构自振频率检测；结构振型检测。试验所需主要仪器设备为：振动及动态信号测试分析系统CRAS7.0；941B 型加速度传感器等。

1.2 试验方案

结构在外部激振影响下会产生随机振动。测量结构上的这种微小随机响应信号，通过频谱分析可以得出该预制板的自振频率和振型等动力特性。试验拟利用导纳法来测试结构的动力特性，导纳法测量结构动力特性已经被多次证明是适合于较低频结构测试的方法[7]。

加速度传感器测点布置一般按照结构振型形状，在变位较大的部位布置测点，尽可能避开各阶振型的节点[8]。因此事先理论计算了结构前3 阶振型的形状，并依此布置结构上的测点位置，结果共设置了18 个测点（图1 所示）。试验采用单点移动测试技术与模态合成技术相结合，固定一个测点（固定第14 号测点）移动另一个测点，通过对结构振动信号的采集与分析获取全结构的模态信息[9]。结构的振动信号拟采集结构的加速度，通过在固定测点处设置的竖向941B 型传感器采集。微小的结构加速度信号通过低通滤波放大器（AZ804）滤波放大，然后由数据采集箱（AZ308）采集，最后通过测试系统的软件分析，得到结构的模态参数。

图1 预制板模态试验测点布置示意图

1.3 试验结果

（1）测点频域波形图及频谱图。通过振动及动态信号测试分析系统采集到各测点的频域波形曲线，为节省篇幅，图2～图5 给出了部分测点的频域波形曲线。

图2 测点4 频域波形曲线

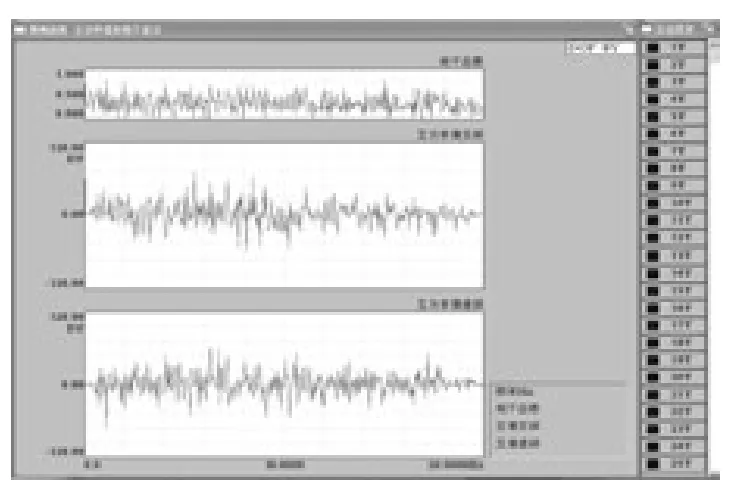
图3 测点8 频域波形曲线

图4 测点12 频域波形曲线

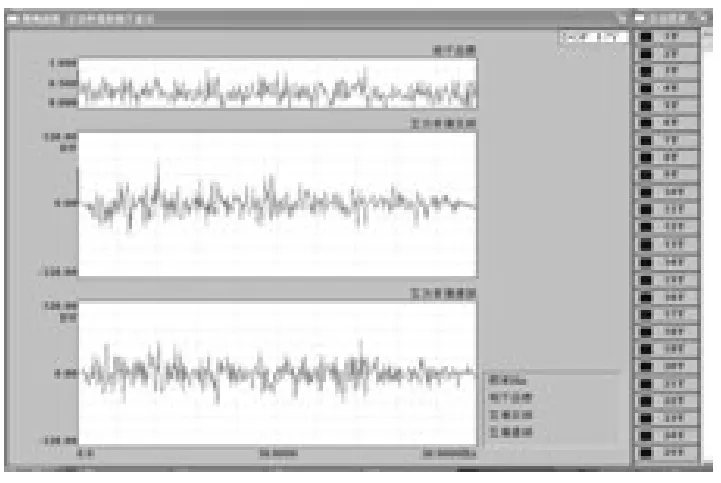
图5 测点16 频域波形曲线

通过测试软件对所采集到的各测点动力响应进行频谱分析，得到预制板全结构的频谱图如图6所示。

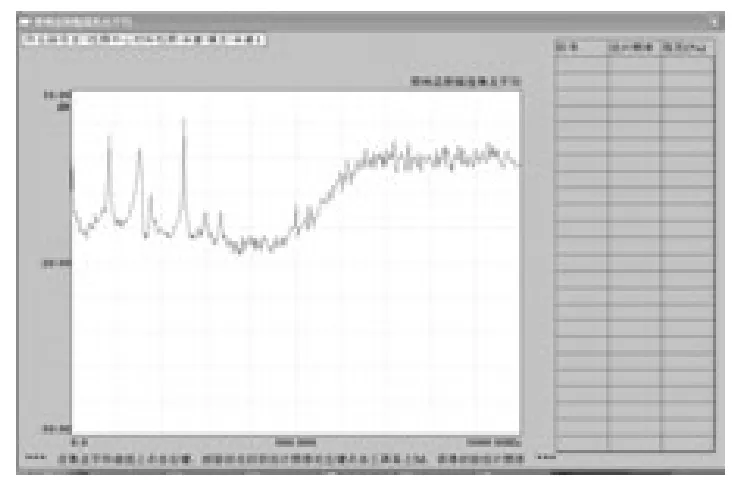
图6 结构频谱图

（2）自振频率与振型。

①理论计算的自振频率与振型。通过ANSYS建模计算[10-12]，该预制板结构的自振频率如表1，相应的理论振型如图7 所示。从结构振型图7 可以看出，结构第一阶振型表现为沿Y 向(结构竖向)的整体上下弯曲振动；第二阶振型表现为沿Y 方向（结构竖向）的反向对称上下振动；第三阶振型表现为Y 方向（结构竖向）的3 波峰对称上下振动[13-15]。

表1 结构理论自振频率

图7 结构理论振型图

图8 一阶模态实测结果-结构整体一阶对称竖弯

图9 二阶模态实测结果-结构二阶反对称竖弯

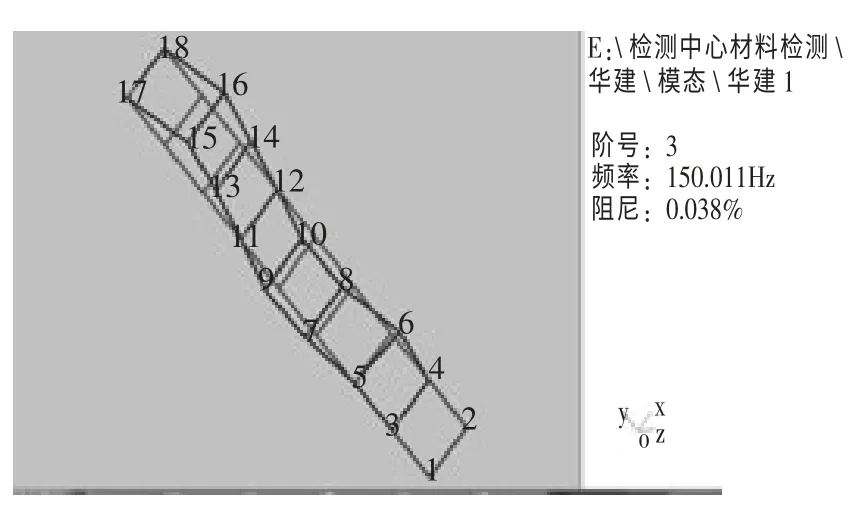
图10 三阶模态实测结果-结构三阶对称竖弯

②实测的自振频率与振型。由上述采集的各测点频域波形图，通过频谱分析，可得出各阶自振频率如表2。前3 阶模态实测结果如图8～图10 所示。

表2 结构实测自振频率

2 结 论

通过对钢筋混凝土预制板进行结构动力模态测试分析，得到以下结论：

采用随机振动的导纳测量方法，所得各阶振动模态分阶清楚，且和理论振型较为吻合，说明本试验所采用的测试方法是可行的，测试结果是可靠的。由模态试验实测基频和理论计算值对比可以看出，实测基频略大于理论计算值，说明结构的实际刚度比理论刚度大，各部件整体性能较好。

[1] 李国强，李杰.工程结构动力检测理论与应用[M].北京：科学出版社，2002.

[2] 林伟平，黄向京，丁立. 钢网面板加筋土挡墙动力特性试验的变形研究[J].公路工程，2011，37（5）：23-28.

[3] 黄向京，王祥，王维，等.双绞合六边形金属网加筋格宾挡墙地震动力特性试验研究[J]. 公路工程，2009，35（5）：36-40.

[4] 张振浩，杨伟军.基于复振型分解的多自由度非线性体系动力可靠性研究[J].地震工程与工程振动，2012，32（3）：8-15.

[5] 刘明.土木工程结构试验与检测[M].北京：高等教育出版社，2008.

[6] 张振浩，杨伟军.基于复模态随机响应的钢筋混凝土梁桥抗震可靠度分析[J]. 桥梁建设，2014，44（1）：69-75.

[7] 孙文波，梁蜜勤.剪力墙结构高阶自振频率计振型的一种近似计算方法[J]. 西北建筑工程学院学报 （自然科学版），2000，17（2）：21-25.

[8] 李杰，李国强.上海金茂大厦结构动力特性测试[J].土木工程学报，2000，33（2）：35-39.

[9] 施卫星，魏丹，韩瑞龙.钢结构房屋动力特性脉动法测试研究[J].地震工程与工程振动，2012，32（1）：56-61.

[10] 任辉启.ANSYS7.0 工程分析实例详解[M].北京：人民邮电出版社，2003.

[11] 郝文化.ANSYS 土木工程应用实例[M].北京：中国水利水电出版社，2005.

[12] 陈精一，蔡国忠. 电脑辅助工程分析ANSYS 使用指南[M].北京：中国铁道出版社，2001.

[13] 薛刚，胡行飞.体外预应力混凝土简支梁固有频率研究[J].广西大学学报(自然科学版)，2012，37（4）：89-93.

[14] 张振浩，杨伟军. 非线性体系动力可靠性分析的等效Duffing 体系法[J].土木建筑与环境工程，2012，34(3)：70-75.

[15] Zhenhao Zhang, Weijun Yang, Zhigang He. Experiment and theory study on ultimate bearing capacity of reinforced concrete tubular hollow continuous slab [J]. Applied Mechanics and Materials, v 204-208, p 782-785，2012.