小流域治理中的复杂水面线计算方法探讨

刘春玲

（宁乡县水土保持预防监督局 长沙市 410600）

1 工程概况

沩水系湘江下游左岸一级支流，发源于宁乡县扶王山，控制流域面积2 430 km2，河长144 km，平均坡降1.16‰。流域内溪沟发达，从西至东贯穿宁乡县境支流多达99 条，其中尤以乌江和楚江为最。

根据工程任务，本次河道治理段位于沩水南源上游，综合治理总长5.6 km。治理项目区地处湖南省三大暴雨地区之一——雪峰山北峰安化梅城一带边缘，属中亚热带向北亚热带过度的大陆性季风湿润气候，水量充沛。

根据调查，目前拟整治河段存在的主要问题有：其一，堤防堤身单薄，加之河道内淤积严重，减少了河流过水断面，一遇较大洪水，则造成洪水漫溢，冲刷两岸堤防；其二，由于河段地处山区，河床坡降大，流速快，水位变化较大，为保护河床、便于两岸农田灌溉，目前河道内建有多座小型河坝。这些河坝多建于20世纪50～70年代，设计标准低，运行至今，均有老化破损情况存在。由于以上原因，致使项目区内洪涝灾害频繁，年年防汛抗灾，耗费大量人力物力，也威胁着当地人民生命财产安全，阻碍了当地农村经济发展。

根据国家《防洪标准》（GB 50201-94）规定，沩水上游河道整治工程等别为Ⅴ等，主要建筑物级别为5级，堤防工程防洪标准采用10年一遇洪水设计。

2 水文计算基础资料

2.1 河段水系

工程区地处宁乡县沩水上游，河段平均坡降J=4.31‰，治理河段全长5.6 km。治理河段起始断面（0+000）集雨面积28.95 km2，断面以上河道长10.42 km，河段内有两条支流汇入主河干道，一支流入汇于桩号1+640 处，汇入口集雨面积48.09 km2，二支流入汇于桩号3+716 处，汇入口集雨面积57.8 km2。图1 为河段水系图。

图1 河段水系图

2.2 河段内涉水工程资料

治理河段地处沩水南源，系山区河流，现状河道蛇曲蜿蜒、阻水河段较多，河道狭窄，河岸边坡冲刷严重。河段内主要分布有多座小型灌溉引水河坝，多为当地村民为解决农田灌溉自发组织建设,上游河段无大型水利工程。根据测量成果，各河坝基本情况见表1。

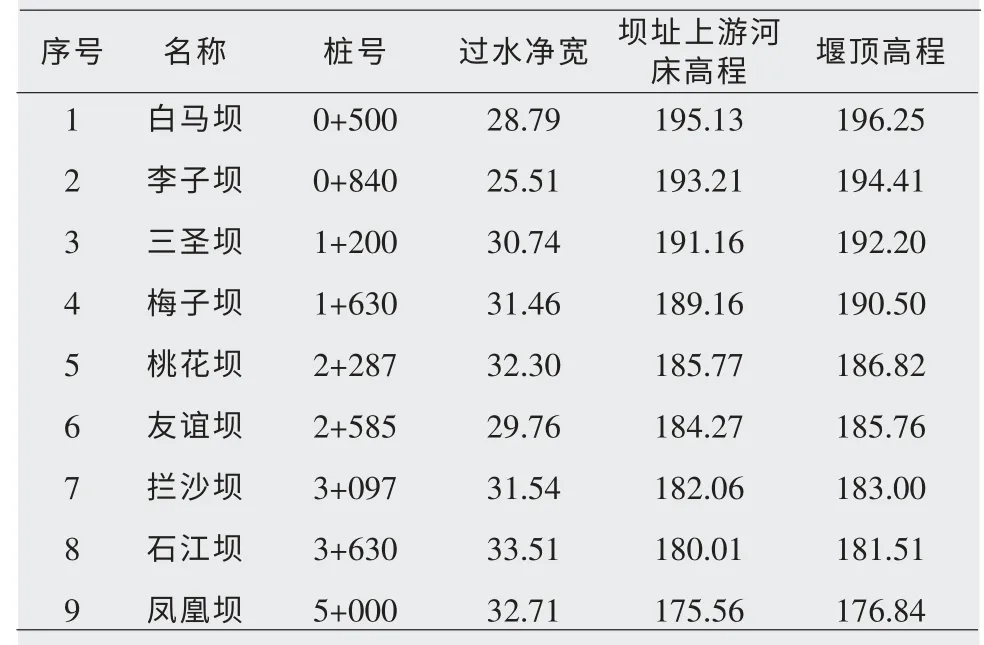
表1 各河坝基本情况 m

3 设计洪水水面线计算步骤

沩水整治河段属于山区河流，根据实地走访勘察，河段堤防洪标准较低，河段内有小型挡水固定坝9 座，对水面线有一定的影响，故水面线计算过程根据实测河道横断面和相应设计洪峰流量，将河段以河坝为界分为若干个计算段落，推算河道设计洪水水面线，具体步骤如下：

第一步，推求设计暴雨及设计洪峰流量。根据《暴雨洪水查算手册》，采用推理公式法或综合单位线法计算洪峰、洪量及洪水过程。

第二步，在河道下游段选择相对顺直、河道比降较缓河段，采用均匀流公式，计算相应的设计洪水位，并以此水位作为水面线计算的起始值。

第三步，以上述起始河道断面为计算断面，从下游向上游根据河道恒定非均匀流基本方程推求河道水面线至整治河段最后一个河坝（凤凰坝）断面下游。

第四步，根据凤凰坝断面过流量、坝下水位高程、堰高、过流宽度等基本数据，利用堰流实用计算公式，核定淹没系数，反推凤凰坝坝上水位。

第五步，将凤凰坝断面作为起始断面，再次从下游向上游根据河道恒定非均匀流基本方程推求河道水面线至整治河段倒数第二个河坝（石江坝）坝下水位。此时，汇流支流由两条变为一条，设计洪峰流量相应减小。

第六步，根据石江坝断面过流量、坝下水位高程、堰高、过流宽度等基本数据，利用堰流实用计算公式，核定淹没系数，反推石江坝坝上水位。

第七步，利用河道恒定非均匀流公式自石江坝断面继续往上游推求……。

以此类推水面线至整治河段起始断面位置。

4 设计洪水水面线计算方法

4.1 设计暴雨及设计洪峰流量计算

切入点：由于沩水整治河段无水文测站，不能直接采用流量资料推求设计洪水，故洪水计算根据《湖南省暴雨洪水查算手册》查取流域暴雨参数，并结合小流域集雨区下垫面条件，合理选取参数，采用推理公式法计算洪水过程。

计算方法：查《湖南省暴雨查算手册》，整治河段属于湖南省暴雨分区第七区，最大24 h 点雨量均值为120 mm，最大24 h 点雨量变差系数Cv＝0.50，偏态系数Cs=3.5 Cv，产流分区属第Ⅰ区，本次采用初损、地表径流系数法进行产流计算，其中初损I 取30 mm，地表径流占总径流的比值Ψ 取0.75。根据上述有关参数求得10年一遇24 h 面暴雨量为197.21 mm。

根据地形参数θ、汇流系数m 及Rt/t 关系曲线，推求P=10%设计洪水见表2。

表2 P=10%设计洪水

4.2 天然河道水面线计算

切入点： 天然河道蜿蜒曲折，过水断面很不规则，断面形状、粗糙系数及河道底坡沿程都有变化，加上河道工程的阻水影响，导致水力因素十分复杂。计算采用水力学中河道水面线的计算原理和方法。

计算原理：首先假设发生设计洪水时，河道水流属于恒定非均匀流，水面线计算采用天然河道水位沿程变化的伯努利能量方程式：

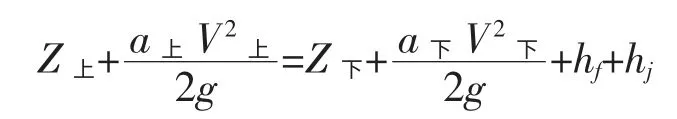
Hf——沿程损失；

Hj——局部损失；

Z上、Z下——上、下断面水位高程。

对于沿程损失hf，目前计算方法比较统一，一般采用以下公式求解：

式中 Q——设计流量；

L——上下断面间距；

A、C、R——符号意义同均匀流公式。

对于局部损失Hj，目前分析计算的方法较多。一般对于河道工程，不同的局部阻水情况有不同的分析计算方法，本次局部损失采用一般水力学法计算，计算式如下：

式中 ξ——局部水头损失系数。对于河道的局部水头损失系数，一般对逐渐收缩的流段，局部损失很小，可以忽略不计；对于扩散的河段，局部损失系数ξ 可取（-0.3～-1）之间，视扩散的急剧程度不同来选择，扩散角较小者可取-0.3，突然扩散可取-1。

V上、V下——上、下游断面流速。

4.3 起始断面水深计算

切入点：在整治河段下游选择相对顺直、河道比降较缓河段断面，通过《水力学》均匀流公式，根据设计洪峰流量Qm计算相应的设计洪水位，并以此水位和流量作为水面线计算的起始值。

计算原理：根据河段实际情况，选取距整治河段下游100 m 的5+700 断面作为水面线起始计算断面。5+700 断面水位流量关系采用均匀流公式Q=计算：

式中 A——过水断面面积，A=（b+mh）h；

m——边坡系数；

n——计算河段平均糙率，根据河床实际情况，查《水力学》渠道及天然河流的糙率n 值表，天然河道糙率取0.04，整治后河道糙率取0.035。

计算成果：起始计算断面（5+700）水位～流量关系曲线见图2。

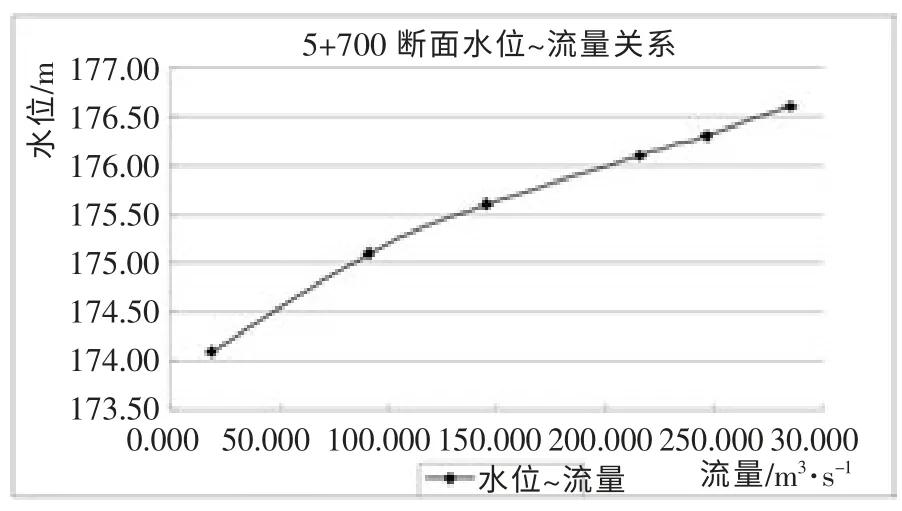
图2 起始计算断面（5+700）水位～流量关系曲线

4.4 河坝堰顶水位高程计算

切入点：已知河坝断面过流量、坝下水位高程、堰高、过流宽度等基本数据，利用宽顶堰实用计算公式，通过反复试算，反推上游坝顶水深H0,计算过坝水位高程。

计算原理：

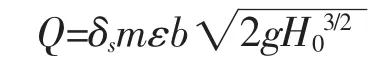
式中 δs——宽顶堰淹没系数，当Hs/H0＞0.8 时，过堰水流为淹没出流，淹没系数δs可查《水力学》表8.2 得；当Hs/H0≤0.8 时，过堰水流为自由出流，淹没系数δs＝1。

a——坝顶入口形状系数，墩头为矩形，堰顶入口为方角时，取a=0.19；

b——坝顶溢流孔净宽；

B——上游河渠宽；

m——流量系数，堰顶入口为方角时，m=0.32+0.01

P1——上游坝高；

H0——上游坝顶水深。

计算成果：由计算可知，整治前，遇设计洪水时，河段内有多座河坝堰流形态为淹没出流，δs≤1；通过清淤加固等综合治理后，遇设计洪水时，堰顶水位有所降低，堰流形态均为自由出游，δs＝1。整治河段内治理前后河坝坝顶水位高程计算成果分别见表3、表4。

5 设计洪水水面线计算成果

整治前河段底宽较窄，断面洲滩淤积严重，部分河段堤防防洪标准不足10年一遇；整治后，通过河段堤防培厚加固，洲滩清淤，工程后河道糙率减小，水面线有所降低。整治前后水面线见图3。

表3 整治前堰顶水位高程计算成果表

表4 整治后堰顶水位高程计算成果表

6 结 语

从以上对小流域治理中复杂水面线的计算推理过程来看，可基本得出如下结论：当天然河道河段内没有控制断面或水文测站时，可利用《暴雨洪水查算手册》计算河段内设计暴雨、设计洪水，以下游断面为初始计算断面逐断往上游推求水面线，起推断面选择治理河段下游河道相对顺直、比降较缓河段，起推断面水深可按均匀流公式进行计算，起推断面往上水面线计算按照天然河道水位沿程变化为恒定非均匀流的伯努利能量方程式进行推算，在推算过程中，如遇坝、闸等小型阻水建筑物，利用宽顶堰实用计算式，以坝下水位为基础，反推堰上水头，计算堰上水位高程，之后继续利用能量方程式计算上游断面水位，如此反复推算直至整治河段起始断面。用此方法推算小流域治理中多支流、多河坝河段水面线，计算成果与实际洪水调查结果基本相符，比较合理。

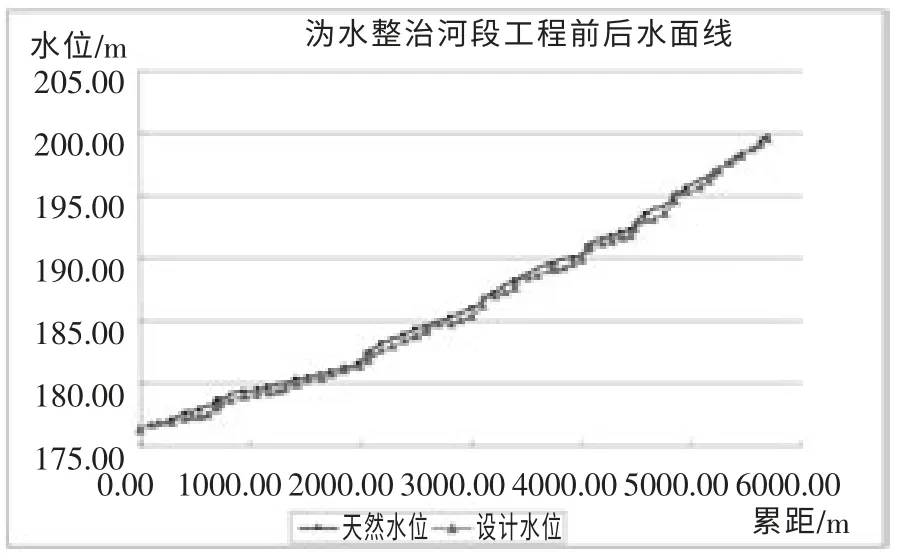
图3 沩水治理河段工程前后水面线图（P＝10%）