基于性能退化信息的系统可靠性建模分析方法
2015-12-24任占勇武月琴李永红
任占勇 武月琴 李永红
(中航工业综合技术研究所,北京 100028)
基于性能退化信息的系统可靠性建模分析方法
任占勇 武月琴 李永红
(中航工业综合技术研究所,北京 100028)
针对系统及其组成单元的性能退化问题,分析了电子产品故障特点,描述了3种基本的性能状态变化行为;研究了性能退化的系统及其组成单元的不同工作状态的确定方法;在此基础上提出了基于通用衍生函数的多状态系统可靠性建模方法。通过构建考虑单元性能退化特征的系统可靠性模型,用多状态刻画系统性能退化的动态变化特征,实现了具有性能退化特征的系统可靠性的精准描述。
性能退化;通用衍生函数;多状态系统
基于现代使用和作战任务的需要,装备及其系统组成结构和功能日益复杂,主要表现在如下几个方面:一是顶层任务具有多样性。系统的使命任务(或具体使用过程中承担的任务)往往具有多样性,多样化带来的问题较为复杂,不易用工作与故障2个状态清楚描述。二是功能单元的任务具有动态性。系统的功能单元的任务是在系统的实际运行过程中,按照运行“规则”动态分配的,功能单元的工作具有多状态性。三是系统及其组成单元的性能具有退化趋势。现有的可靠性建模分析技术在解决具有上述特点的系统可靠性分析与设计问题时存在诸多不足。如系统被假设为二态系统即只有正常工作与完全失效2种状态,这样的假设对复杂系统而言过于简单。复杂系统在工作过程中呈现出结构复杂、多状态和性能退化的特点,如卫星单元的失效会造成系统性能的降低,以及系统完成任务能力的降低,而不是整个系统的失效或任务的失败。如果不考虑系统组成单元及自身的性能退化仍利用二态系统可靠性分析方法对其分析,很难准确地描述系统性能降低或失效的内在原因。
可靠性建模是可靠性工作的重要组成部分,是实现可靠性预计、可靠性分配以及可靠性评估等的前提条件。对于复杂系统,如果没有正确的、可用的可靠性建模分析方法,在设计阶段将不能对其可靠性进行分配和预计,从而导致不能进行正确的设计,因此,也不能进行可靠性设计评价;在定型阶段,会产生任务可靠性的约束条件难以界定,从而导致任务可靠性无法验证。复杂系统由于其技术含量高以及系统内子系统和单元运行过程的复杂性等特点,其可靠性分析牵涉因素繁多,需要围绕可靠性要求及其资源约束,对可靠性相关的工作项目及其工程过程活动进行系统规划、实施和控制,而可靠性建模分析技术是实施系统可靠性工程的关键基础技术。
多状态系统主要分为2种:多工作状态系统和多性能水平系统[1]。多工作状态系统是指系统除了正常工作和完全失效2种状态外,还具有多种工作状态,如n中取k系统就是典型的多工作状态系统。多性能水平系统是指系统能够在多种性能水平下运行。如核动力装置的设计寿命一般很长,但随着运行时间的增加,由于设备的老化、磨损或维修管理不当等原因,部分设备的性能会出现退化,整个装置的技术状态呈下降趋势,呈现出多种性能水平。多态系统可靠性分析方法主要有4种:布尔模型扩展方法,随机过程方法(主要是Markov过程方法),Monte Carlo 仿真方法和通用生成函数方法[2]。通用衍生函数法是计算多状态系统可靠性的有效方法,解决了多种具体系统的可靠性建模问题[3-7]。
本文针对系统及其组成单元的多态性及性能退化问题,在分析性能退化的系统及其组成单元的状态确定方法的基础上,研究了基于通用衍生函数的多态系统可靠性建模方法。可为装备复杂系统可靠性设计分析和指标的准确评价提供技术与方法支撑。
1 电子产品使用过程中的性能状态变化分析
1.1 电子产品性能状态变化的几种基本形式
所有产品的故障都是由于其在使用过程中受到内外部因素的影响所导致。由于判别电子产品故障的判据是以其一个或多个性能参数或逻辑参数来表征的,因此电子产品的故障过程可以理解为其性能参数或逻辑参数偏离设计目标的状态变化过程[8],其基本趋势包括以下几种情形:
A、渐变的性能状态变化,例如电子设备的电性能参数随着时间的漂移,如图1所示。

图1 电子设备性能参数渐变的性能劣化示意图
B、跳变的性能状态变化,如电过应力导致的瞬时击穿致使电子设备丧失输出信号,或互联、引脚等累积疲劳断裂造成的开路等。该性能跳变过程是一个无时间的瞬时过程,如图2所示。

图2 电子设备性能参数跳变的性能劣化示意图
C、非单调的性能状态变化,如电子设备常存在的间歇性故障,是在一定的条件或激励下发生的故障。当相关条件不存在时,故障不表现出来,如图3所示。

图3 电子设备性能参数非单调性的性能劣化示意图
当然由于各种随机因素的影响,其性能变化还必须考虑随机离散性。电子产品在实际使用过程中由于其组成元器件繁多,环境多样,因此产品性能状态变化往往是由于以上几种趋势组合而成的。
1.2 性能状态变化的原因分析
一般地,电子产品性能参数发生偏离总是由于组成产品的元器件或基本功能单元性能参数偏移或发生局部故障的结果,这些局部的故障或局部性能通过产品的功能拓扑结构关系,传递到其他接口功能单元、上一层次产品直至产品顶层,最终对电子产品输出的性能参数产生影响。由于电子设备的设计特征(例如冗余和重构特征等),某一组成单元的故障或参数偏离未必立即对输出产生影响,而是取决于故障触发条件(如另一冗余单元也故障或发生明显参数偏离)。
从导致电子产品性能变化的原因角度,电子产品性能变化趋势可分为2种类型:一类是有明显趋势的状态变化过程,可以找到相应的表征性能变化的参数;另一类是无时间历程的瞬时性能状态改变,又可根据具体原因细分为2种类型,一种是由于内外因条件触发的故障类型(如过应力故障,或其他条件触发的故障); 另一种是由于互联或管脚疲劳累积损伤所导致,从量变到质变引发的性能状态的突然改变。
2 具有性能退化特点的产品的状态确定方法
性能退化产品从正常工作到完全失效是一个逐渐退化的过程,这里的产品既可指系统又可代表其组成单元。连续型性能水平产品的状态定义要依据其性能水平的取值区间,将连续型性能水平产品离散化为离散型多性能水平产品,从而进行状态定义。由于系统组成单元连续性能参数的离散化是为了计算系统的可靠性,因此,单元离散化时应考虑与系统状态之间的对应关系。在没有相关信息时,可采用下列方法对产品的连续型性能水平进行离散化:
设表征产品性能的参数为X(t),其最大值与最小值分别记为:,将区间分为n等份,每一份确定产品的一个状态。若将分点记为:,则区间分别对应产品的n个状态。当产品性能的参数X(t)属于那个区间时,就称产品处于相应的状态。比如,当时,就称产品处于状态1。
3 具有性能退化特点的系统可靠性建模方法
系统处于状态j或 j之上的概率Rsj的算法如下:
步骤 1 对于i=1,2,…,j,定义如下的u函数Ui1(z):

其中it∈{1,2,…,M},t=1,2,…,n。为了得到关于u函数的详细性质,读者可以参看文献[2]。
步骤 2 对于给定的i构造集合Ei
(1)令集合Ei1为:

其中Pl(t)是从t个到第t+kj–1这kj个连续单元处于状态l的概率,作用在r–维向量与实数y将得到一个(r+1)–维向量。例如。
(3) 如果m≤n–kj+1在u函数Uim(z)中去掉所有满足的项,并构造集合Eim,

根据下面的关系式,计算系统处于状态j的概率rsj, 其中j=0,1,2,…,M。
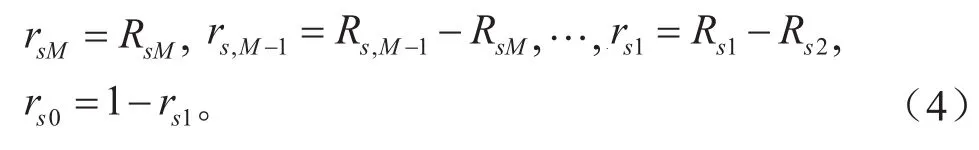
4 案例分析
一个由3个单元组成的线形多状态(C(k,n:G))系统,单元1的性能参数取值区间为[A1,B1],单元2的性能参数取值区间为[A2,B2],单元3的性能参数取值区间为[A3,B3],系统的性能参数取值区间为[A,B],其中A1,A2,A3, 分别表示单元1、单元2、单元3和系统的性能阈值,B1,B2,B3,B分别表示单元1、单元2、单元3和系统的性能初始值,并且系统与单元的性能参数是关于时间的递减函数。按照单元性能参数与系统性能参数之间的关系,将系统与单元分别离散化为4种状态,记为0,,in1∈,{02,,1,23,,…相M应},数据如下:

求系统处于不同状态的概率。
解: 3个多状态元件的u函数分别为:

1)系统处于状态1或1以上的概率的计算由于k1=3=n,

2)系统处于状态2或2以上的概率由于k2=2,

根据U21(z)中所有满足(i1,i2)≥(2,2)的项,可得

根据公式(3)可得:

3)系统处于状态3或3以上的概率由于k3=1,
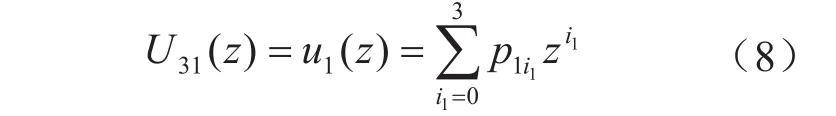
在U31(z)中i1≥3的项是p13z3,可得:
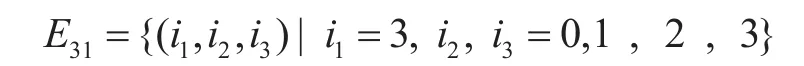



根据公式(3)可得:

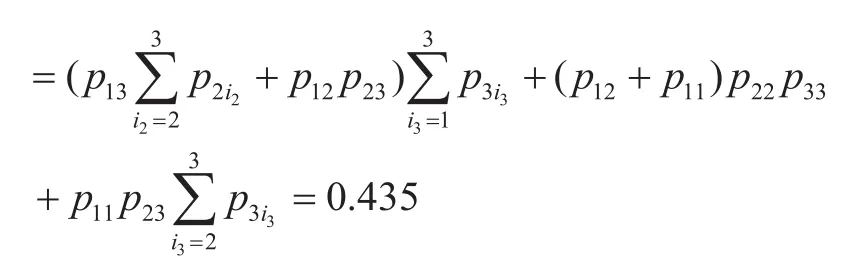
4) 系统处于不同状态的概率根据公式(4)可得:

5 结论
本文提出的具有性能退化特征的系统及其组成单元的状态确定方法,及基于通用衍生函数的多态系统可靠性建模方法,可以有效解决具有性能退化特征的复杂系统可靠性建模问题。但系统可靠性评价结果的准确性还受系统及其组成单元的性能退化信息的影响。而系统及其组成单元的性能退化信息需要通过大量试验或外场使用信息进行积累。
[1] Ross S M. Multivalued State Component Systems[C]. Annals of Probability,1979,7: 379-383.
[2] Lisnianski A.,Levitin G. Multi-state System Reliability Assessment,Optimization and Applications[M]. Singapore: World Scientific,2003.
[3] Levitin G. A Universal Generating Function Approach for the Analysis of Multi-state Systems with Dependent Elements[J]. Reliability Engineering and System Safety,2004,84: 285-292.
[4] Yeh W.C. The k-out-of-n acyclic Multistate-node Networks Reliability Evaluation Using the Universal Generating Function Method [J]. Reliability Engineering and System Safety,2006, 91(7): 800-808.
[5] Levitin G. Linear Multi-state Sliding-window Systems[J]. IEEE Transactions on Reliability,2003, 52(2): 263-269.
[6] Levitin G. Optimal Allocation of Elements in a Linear Muti-state Sliding Window System[J]. Reliability Engineering and System Safety,2002, 76: 245-254.
[7] Levitin G. Uneven Allocation of Elements in Linear Multi-state Sliding Window System[J]. European Journal of Operational Research,2005,163: 418-433.
[8] Li Yong-hong,Zhang Hui,Wang Tao,Physics of Failure Based Reliability Modeling Framework For Electronics. 10th International Conference on Reliability,Maintainability and Safety (Guangzhou), 2014.
[9] Huang J.,Zuo M.J.,Fang Z. Multi-state Consecutive-k-out-of-n Systems[J]. IIE Transactions, 2003, 35: 527-534.
(编辑:劳边)
TB114.2
A
1003–6660(2015)04–0036–05
10.13237/j.cnki.asq.2015.04.010
2015-06-09
