压电叠层梁的动力精确解

芦远腾，何博文，关 群

（1.合肥工业大学 土木与水利工程学院，安徽 合肥230009，2.西安交通大学 能源动力与工程学院，陕西 西安710049）

0 引 言

智能材料是对于外界环境的刺激，可以进行感知并加以判断、分析、处理，产生自主响应（如自我感知、自我诊断、自我修复、自我适应等）具有智能特征的材料［1］。压电材料是目前智能材料中最常见的一种，在结构的振动、噪声、形状控制以及监测结构损伤等领域均得到了广泛的应用［2］。如今以压电材料为代表的智能材料，已在一些重要工程结构的监测、控制及损伤愈合等方面发挥重要的作用，对其的动力学研究也变得十分重要。由于目前的研究主要建立在变分法和有限单元法基础上，计算量大，不适宜计算机编程计算，且有些人为假定，准确度不适宜大型工程结构计算应用，精度不能保证。

状态空间方法以弹性力学三大基本方程为基础，抛弃所有人为的位移模式和应力分布的假设，直接导出传递矩阵，得到压电叠层梁上下两个表面的状态空间变量，这些变量恰好是层间需要满足的位移和应力连续条件的状态变量。这种方法特别适用于叠层梁的求解，而且不受厚度的限制，在叠层构件的求解中得到了广泛应用［3］。本文在弹性材料状态空间解的基础上，结合压电材料的基本方程，得到压电材料的传递矩阵，进而推导出压电叠层梁的状态变量空间解。

1 压电单层梁自由振动的状态方程

如图1所示的简支压电单层梁，材料为弹性压电材料。

1.1 本构关系［4－8］：

1.2 运动方程

设压电材料的密度为ρ。在忽略体力、体电流和体电荷的情况下，梁的运动方程为：

1.3 梯度方程

1.4 简支压电单层梁自由振动的状态方程

压电单层梁的自由振动分析，首先把式（3）、（4）代入式（1）、（2）中，考虑到平衡方程与本构方程中涉及到的8个变量不是相互独立。利用方程（1）～（4）消除σx、Dx，以u、w 、σz、τxz、φ、Dx作为状态变量，得到一组只含有这6个状态变量的偏微分方程组：

Dz是圆频率

将相应状态变量按下列级数项展开：把状态变量的级数表达式带入（5），得：

其中

根据矩阵理论及弹性力学相关知识，式（6）的解为

设G（z）＝eG·z

则

式（11）即为简支压电单层梁的状态空间方程。

2 简支压电叠层梁自由振动的状态方程

如图2所示的简支压电叠层梁，一共有p层，每一层均压电材料。图3是其中任一层j的放大图。在局部坐标系图3中，每一层实际上就是一个单层梁。对于其中的每一层，可得到［9］

其中

在（11）式中，令z＝hj，得

Gj（hj）为六阶矩阵，与每层的材料属性有关。式（13）实际上通过矩阵Gj（hj）把第j层上、下表面六个状态变量联系起来。式（13）对任意一层都成立。当j＝1，2时，分别有

R1（h1）是第一层下表面六个状态变量，而R2（0）是第二层上表面六个状态变量。根据应力连续和层间位移条件，这二组状态变量应该相等，即

考虑上式，把（14）式代入（15）式，得

以此类推，可用传递矩阵把整个叠层梁上、下表面状态变量联系起来，得

则（16）式变成

式中R1（0）为第一层上表面的状态变量，而 ∏为六阶矩阵，将式（17）写成显式，得

对于压电叠层梁的自由振动问题，以梁上下表面均闭路为例，得到的电学与力学边界条件为：τzm（0）＝φm（0）＝0，σzm（h）＝τzm（h）＝φm（h）＝0，则（18）式成为

式（19）实际上是六个代数方程，包含六个未知量um（0），wm（0），um（h），wm（h），Dzm（0），Dzm（h）。现取出第3、4、5行，组成新的方程组，经化简后，得

此时式（20）中ω≠0，由于um（0），wm（0）不全为0，得方程

方程（21）为一个关于ω超越方程，对于不同的m值，均能解出相应的自振频率。

3 数值算例

设有三层简支压电叠层梁，高0.01m，长为0.4m，三层等厚，第一、三层为PZT－5压电陶瓷，第二层为Al，梁上下表面闭路，则相应的电学边界条件为φm（0）＝φm（h）＝0，相应的应力边界条件为σzm（h）＝τzm（h）＝τzm（0）＝0，用本文方法（MATLAB软件）计算梁的自振频率并与文献［10］对比。

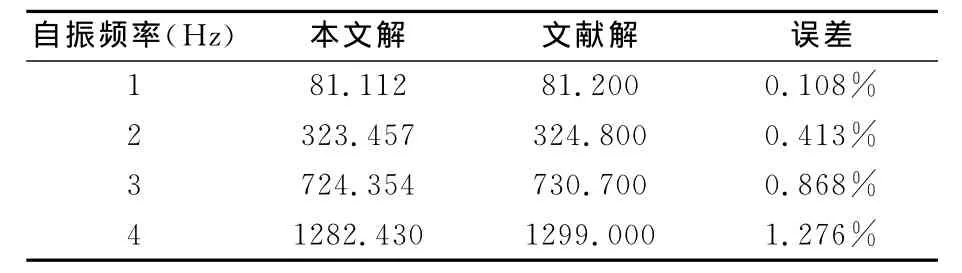
表1 梁的自振频率对比

由表1中的误差计算可知，本文关于压电叠层梁自振频率的精确解与文献资料十分接近。基于状态空间法的叠层梁动力问题的解答准确方便，满足精度要求。

4 结论与讨论

本文采用状态空间方法，以压电材料的本构方程为基础，从状态空间微分方程导出传递矩阵，由此推导出压电叠层梁的自振频率方程。本文方法有以下优点：

（1）状态空间法以弹性力学三大基本方程为基础，抛弃所有人为的位移模式和应力分布的假设，得到压电叠层梁自振频率，此方法解答准确，收敛速度较快。

（2）状态空间法能够求解弹性力学所不能求解的压电叠层梁，并且不受厚度与层数的限制。

（3）在状态空间法中计算中全部采用矩阵的数学表达，大大简化了计算过程，适合计算机编程计算。

1 杨大智.智能材料与智能系统［M］.天津：天津大学出版社，2000.

2 卿光辉，邱家俊，塔娜.压电体的混合变分原理及叠层板的自由振动分析［J］.振动工程学报，2004，17（3）：285－290.

3 王德才，关群，范家让.任意厚度具有自由边叠层板的精确解析解 ［J］.应用数学和力学，2003，34（7）：672－686.

4 慕欣.智能材料球对称问题的研究［D］.合肥：合肥工业大学，2003.

5 薛大为.板壳理论［M］.北京：北京工业学院出版社，1988.

6 Chee C Y，Tong L Y，Steven G P.A review on the modeling of piezoelectric sensors and actuators incorporated in intelligent Structures［J］.Journal of Intelligent Material Systems and Struetures，1998，9（1）：3－9.

7 Tzou H S，Zhong J P.Electromechanics and vibrations of piezoelectric shell distributed systems ［J］.Journal of Dynamic Systems，Measurement and Control，ASME，1993，115（3）：506－517.

8 徐芝纶.弹性力学（上册）［M］.第3版.北京：人民教育出版社，1992：48－68.

9 范家让.强厚度叠层板壳的精确理论［M］.北京：科学技术出版社，1996.

10 Krommer M.On the correction of the Bernoulli－Euler beam theory for smart piezoelectric beams［J］.Smart Materials and Structures，2001：10（4），668.